动态规划-----背包类问题(0-1背包与完全背包)详解
目录
什么是背包问题?
动态规划问题的一般解决办法:
0-1背包问题:
0 - 1背包类问题 分割等和子集:
完全背包问题:
完全背包类问题 零钱兑换II:
什么是背包问题?
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。也可以将背包问题描述为决定性问题,即在总重量不超过W的前提下,总价值是否能达到V?它是在1978年由Merkle和Hellman提出的。
动态规划问题的一般解决办法:
动态规划,无非就是利用历史记录,来避免我们的重复计算。而这些历史记录,我们得需要一些变量来保存,一般是用一维数组或者二维数组来保存。下面我们先来讲下做动态规划题很重要的三个步骤:
- 🧐 步骤一:定义dp数组元素的含义
- 🧐步骤二:找出数组元素之间的关系式(也就是我们所熟知的状态转移方程)
- 🧐第三步骤:找出初始值(base case)
接下来的题目我们会按照这三个步骤来解释说明
前言:本文包含动态规划中的经典背包问题,有关背包问题的描述如下:
在动态规划中,背包问题是一个经典的优化问题,它可以分为0-1背包问题和完全背包问题两种类型。下面我们就来看看这两个问题:
0-1背包问题:
问题描述:
给你一个可装载重量为 W 的背包和 N 个物品,每个物品有重量和价值两个属性。其中第 i 个物品的重量为 wt[i],价值为 val[i]。现在让你用这个背包装物品,每个物品只能用一次,在不超过被包容量的前提下,最多能装的价值是多少?

- 🧐 步骤一:定义dp数组元素的含义:
由于状态有两个,就是「背包的容量」和「可选择的物品」,这里我们就需要用到一个二维的dp
数组,如下为dp数组的定义:
🦉🦉🦉dp[i][w] 的定义如下:对于前 i 个物品,当前背包的容量为 w,这种情况下可以装的最大价值是 dp[i][w]
- 🧐步骤二:找出数组元素之间的关系式(也就是我们所熟知的状态转移方程)
1.如果你没有把这第 i 个物品装入背包,那么很显然,最大价值 dp[i][w] 应该等于 dp[i-1][w],继承之前的结果(翻译一下就是不装入第i个物品,相当于对前 i - 1 个物品进行选择,对应此时的背包容量w)。即此时的状态转移方程是:dp[ i ][ w ] = dp[ i - 1 ][ w ]
2.如果你把这第 i 个物品装入了背包,此时背包剩余容量为 w - wt[ i - 1 ](wt数组下标是从0开始的, wt[ i - 1 ] 相当于第 i 个物品的重量,val 也一样)
则此时的状态转移方程是:dp[ i ][ w ] = dp[ i - 1 ][ w - wt[ i - 1] ] + val[ i - 1 ]
- 🧐第三步骤:找出初始值(base case):
这题的base case 相对简单,当物品个数为0或则背包当前容量为0时,dp[ i ][ w ] 都等于0
按照上述的状态转移方程,我们可以填出对应dp表格(以图中的例子为例):

有了上述铺垫后,动态规划的代码就很好实现了,具体代码如下:
int knapsack(int W, int N, int[] wt, int[] val) {assert N == wt.length;// base case 已初始化,数组自动全部初始化为0int[][] dp = new int[N + 1][W + 1];for (int i = 1; i <= N; i++) {for (int w = 1; w <= W; w++) {if (w - wt[i - 1] < 0) {// 这种情况下只能选择不装入背包dp[i][w] = dp[i - 1][w];} else {// 装入或者不装入背包,择优dp[i][w] = Math.max(dp[i - 1][w - wt[i-1]] + val[i-1], dp[i - 1][w]);}}}return dp[N][W];
}
有了上面的一定了解后,我们来看看0 - 1背包的类似题:
0 - 1背包类问题 分割等和子集:
看一下力扣第 416 题「分割等和子集open in new window」:
题目描述:输入一个只包含正整数的非空数组 nums,请你写一个算法,判断这个数组是否可以被分割成两个子集,使得两个子集的元素和相等。对应函数签名如下:

我们可以将这个问题转化为0 - 1背包问题,具体做法:
这个问题相当于给一个可装载重量为 sum / 2 的背包和 N 个物品,每个物品的重量为 nums[i]。现在让你装物品,是否存在一种装法,能够恰好将背包装满?按照上述解题思路就是:
- 🧐 步骤一:定义dp数组元素的含义:
dp[i][j] = x 表示,对于前 i 个物品(i 从 1 开始计数),当前背包的容量为 j 时,若 x 为 true,则说明可以恰好将背包装满,若 x 为 false,则说明不能恰好将背包装满。
- 🧐步骤二:找出数组元素之间的关系式(也就是我们所熟知的状态转移方程)
与上面类似,这里就直接给出来了:
1.不把这第 i 个物品装入背包:dp[ i ][ j ] = dp[ i - 1 ][ j ]
2.把这第i个物品装入背包:dp[ i ][ j ] = dp[ i - 1][ j - nums[ i - 1 ] ]
- 🧐第三步骤:找出初始值(base case):
当背包容量为0时(sum / 2= 0)这时无论物体有多少个都可以满足条件,就是什么都不装嘛
ok,接下来看完整代码:
boolean canPartition(int[] nums) {int sum = 0;for (int num : nums) sum += num;// 和为奇数时,不可能划分成两个和相等的集合if (sum % 2 != 0) return false;int n = nums.length;sum = sum / 2;boolean[][] dp = new boolean[n + 1][sum + 1];// base casefor (int i = 0; i <= n; i++)dp[i][0] = true;for (int i = 1; i <= n; i++) {for (int j = 1; j <= sum; j++) {if (j - nums[i - 1] < 0) {// 背包容量不足,不能装入第 i 个物品dp[i][j] = dp[i - 1][j];} else {// 装入或不装入背包dp[i][j] = dp[i - 1][j] || dp[i - 1][j - nums[i - 1]];}}}return dp[n][sum];
}
完全背包问题:
完全背包问题与0-1背包问题类似,但不同之处在于每个物品可以选择放入背包多次(数量无限),即每个物品的选择是一个无限的选择。我们给出对应的解题方法:
- 🧐 步骤一:定义dp数组元素的含义:
若只使用前 i 个物品(可以重复使用),当背包容量为 j 时,能装入背包的最大价值为dp[i][w]
- 🧐步骤二:找出数组元素之间的关系式(也就是我们所熟知的状态转移方程)
1.不将第i个物品装入背包,此时:dp[ i ][ w ] = dp[ i - 1 ][ w ]
2.将第i个物品装入背包,此时:dp[ i ][ w ] = dp[ i ][ w -wt[ i - 1] ] + val[ i - 1 ]
- 🧐第三步骤:找出初始值(base case):
这题与0 - 1的bas背包的base case 一致,当物品个数为0或者背包当前容量为0时,dp[ i ][ w ] 都等于0
对应的动态规划代码为:
int fullBackpack(int W, int N, int[] wt, int[] val) {assert N == wt.length;// base case 已初始化,数组自动全部初始化为0int[][] dp = new int[N + 1][W + 1];for (int i = 1; i <= N; i++) {for (int w = 1; w <= W; w++) {if (w - wt[i - 1] < 0) {// 这种情况下只能选择不装入背包dp[i][w] = dp[i - 1][w];} else {// 装入或者不装入背包,择优dp[i][w] = Math.max(dp[i][w - wt[i-1]] + val[i-1], dp[i - 1][w]);}}}return dp[N][W];
}
完全背包类问题 零钱兑换II:
这是力扣第 518 题「零钱兑换 IIopen in new window」,题目描述:
给定不同面额的硬币 coins 和一个总金额 amount,写一个函数来计算可以凑成总金额的硬币组合数。假设每一种面额的硬币有无限个。对应函数签名如下:

我们可以把这个问题转化为完全背包问题的描述形式:
有一个背包,最大容量为 amount,有一系列物品 coins,每个物品的重量为 coins[i],每个物品的数量无限。请问有多少种方法,能够把背包恰好装满?按照动态规划三步走:
- 🧐 步骤一:定义dp数组元素的含义:
dp[i][j] 的定义如下:若只使用前 i 个物品(可以重复使用),当背包容量为 j 时,有 dp[i][j] 种方法可以装满背包。
- 🧐步骤二:找出数组元素之间的关系式(也就是我们所熟知的状态转移方程)
1.如果你不把这第 i 个物品装入背包,也就是说你不使用 coins[i-1] 这个面值的硬币,那么凑出面额 j 的方法数 dp[i][j] 应该等于 dp[i-1][j],继承之前的结果
即状态转移方程为:dp[ i ][ j ] = dp[ i -1 ][ j ]
2.如果你把这第 i 个物品装入了背包,也就是说你使用 coins[i-1] 这个面值的硬币,那么 dp[i][j] 应该等于 dp[i][j-coins[i-1]]。
即状态转移方程为:dp[ i ][ j ] = dp[ i ][ j - coins[ i - 1] ]
- 🧐第三步骤:找出初始值(base case):
base case 为 dp[0][..] = 0, dp[..][0] = 1。i = 0 代表不使用任何硬币面值,这种情况下显然无法凑出任何金额;j = 0 代表需要凑出的目标金额为 0,那么什么都不做就是唯一的一种凑法。
写出动态规划代码:
int change(int amount, int[] coins) {int n = coins.length;int[][] dp = int[n + 1][amount + 1];// base casefor (int i = 0; i <= n; i++) dp[i][0] = 1;for (int i = 1; i <= n; i++) {for (int j = 1; j <= amount; j++)//装入背包或者不装入,加起来if (j - coins[i-1] >= 0)dp[i][j] = dp[i - 1][j] + dp[i][j - coins[i-1]];else // < 0 只能选择不装入背包dp[i][j] = dp[i - 1][j];}return dp[n][amount];
}
结语: 写博客不仅仅是为了分享学习经历,同时这也有利于我巩固自己的知识点,总结该知识点,由于作者水平有限,对文章有任何问题的还请指出,接受大家的批评,让我改进。同时也希望读者们不吝啬你们的点赞+收藏+关注,你们的鼓励是我创作的最大动力!

相关文章:

动态规划-----背包类问题(0-1背包与完全背包)详解
目录 什么是背包问题? 动态规划问题的一般解决办法: 0-1背包问题: 0 - 1背包类问题 分割等和子集: 完全背包问题: 完全背包类问题 零钱兑换II: 什么是背包问题? 背包问题(Knapsack problem)是一种…...

通过 Docker 搭建 BookStack
文章目录 环境说明1、官方网站2、通过 Docker 部署总结 环境说明 操作系统版本:CentOS Linux release 7.9.2009 (Core) Docker 版本:Docker Engine - Community 24.0.2 BookStack 版本:23.02.3 MySQL 版本:8.0.32 1、官方网站 G…...
?它的主要作用是什么?)
通俗易懂:什么是Java虚拟机(JVM)?它的主要作用是什么?
Java虚拟机(Java Virtual Machine, JVM)是一种软件实现的抽象计算机,它负责执行Java字节码(Bytecode)。Java程序并不是直接在物理计算机上运行,而是先由Java编译器将源代码编译成与平台无关的字节码&#x…...
)
[k8s] kubectl执行失败后等待一段时间再重试 (Shell实现)
使用Shell脚本实现功能: kubectl执行失败后,等待30秒后再重试,一共重试3次,代码如下: #!/bin/bashKUBECTL_BIN/var/lib/snapd/snap/bin/kubectlERR_MSG_K8S_NOTRUNNING"microk8s is not running" ERR_MSG_C…...

java中的static和单例模式
同一个类中,访问其类成员,可以省略类名不写 static:叫静态,可以修饰成员变量,成员方法。 成员变量按照有无static修饰,分为两种: 类变量:有static修饰,属于类…...

RabbitMQ相关总结
Broker 异步调用中用Broker进行事件订阅和调用,完成解耦 没有强依赖,不用担心级联失败 流量削峰 MQ 的下载 1.可以使用命令拉取镜像 docker pull rabbitmq:3-management 2.也可以直接去官网下载tar包,然后上传到虚拟机上面 spring AMQP…...

RAFT: Adapting Language Model to Domain Specific RAG
今天来介绍下伯克利大学3.15日新发的一篇paper,RAFT: Adapting Language Model to Domain Specific RAG 主要研究了如何构造训练数据来微调你的LLM,从而在LLM在垂直领域的RAG中表现更好。并且开源了代码:GitHub - ShishirPatil/gorilla: Gorilla: An API store for LLMs 主…...
第十五届蓝桥杯第三期模拟赛第十题 ← 上楼梯
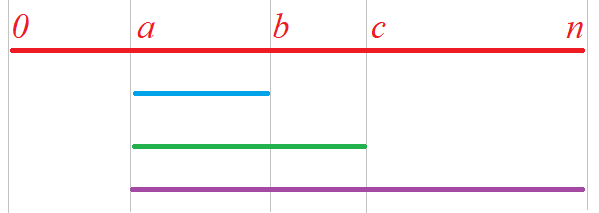
【问题描述】 小蓝要上一个楼梯,楼梯共有 n 级台阶(即小蓝总共要走 n 级)。小蓝每一步可以走 a 级、b 级或 c 级台阶。 请问小蓝总共有多少种方案能正好走到楼梯顶端?【输入格式】 输入的第一行包含一个整数 n 。 第二行包含三个整…...

第四题:星期一
题目描述 本题为填空题,只需要算出结果后,在代码中使用输出语句将所填结果输出即可。 整个 20 世纪(1901 年 1 月 1 日至 2000 年 12 月 31 日之间),一共有多少个星期一?(不要告诉我你不知道今天是星期几…...

Mamba: Linear-Time Sequence Modeling with Selective State Spaces(论文笔记)
What can I say? 2024年我还能说什么? Mamba out! 曼巴出来了! 原文链接: [2312.00752] Mamba: Linear-Time Sequence Modeling with Selective State Spaces (arxiv.org) 原文笔记: What: Mamba: Linear-Time …...
)
2024蓝桥杯每日一题(区间DP)
备战2024年蓝桥杯 -- 每日一题 Python大学A组 试题一:游戏 试题二:石子合并 试题三:密码脱落 试题四:能量项链 试题一:游戏 【题目描述】 玩家一和玩家二共同玩一个小游戏。给定一个包含 N 个…...

LeetCode-2952. 需要添加的硬币的最小数量【贪心 数组 排序】
LeetCode-2952. 需要添加的硬币的最小数量【贪心 数组 排序】 题目描述:解题思路一:看提示主要是用贪心和排序。那我们肯定是首先对coins排序。然后依次遍历coins[i],获取当前可以获取金额范围,和判断是否加入新硬币。判断规则如下…...

新书速递——《可解释AI实战(PyTorch版)》
本书旨在帮助你实施最新的可解释AI技术,以构建公平且可解释的AI系统。可解释AI是当今AI研究中的热门话题,但只有少数资源和指南涵盖了所有重要技术,这些技术对实践者来说非常有价值。本书旨在填补这一空白。 本书读者对象 本书既适合那些有兴…...

国产数据库中统计信息自动更新机制
数据库中统计信息描述的数据库中表和索引的大小数以及数据分布状况,统计信息的准确性对优化器选择执行计划时具有重要的参考意义。本文简要整理了下传统数据库和国产数据库中统计信息的自动更新机制,以加深了解。 1、数据库统计信息介绍 优化器是数据库…...

【C++】入门C++(中)
好的,我们继续,这是 C专栏的第二篇博客,还没读过上一篇博客可以进入我创建的专栏阅读 入门C(上)再回来哦~ 下面我们要讲的第一个概念就是函数重载 函数重载 1. 函数重载概念 什么是函数重载? 简单来说…...
javaIO
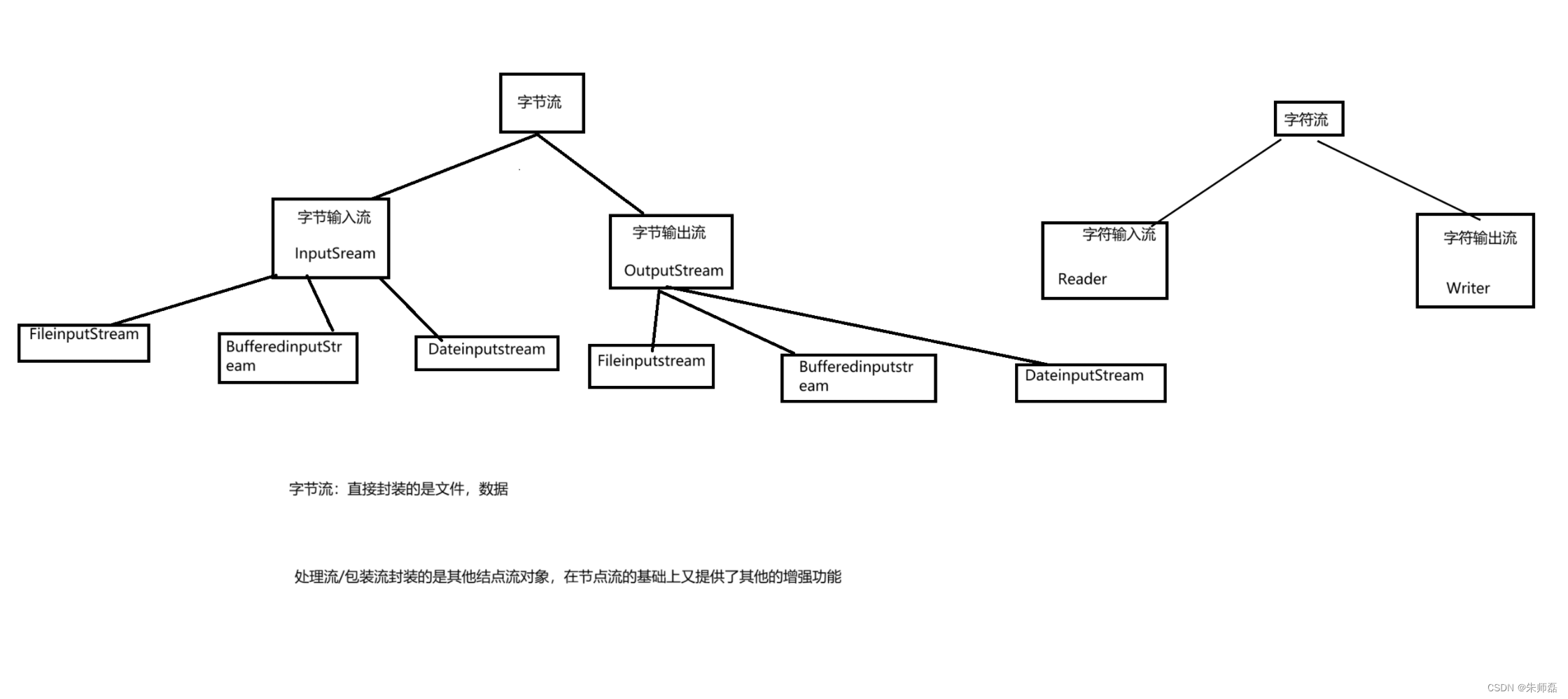
file类 一个File类的对象可以表示一个具体的文件或目录 mkdir 创建单级文件夹 mkdirs 创建多级文件夹 delete 删除一个文件夹时,文件夹里面必须是空的 listfiles 将文件夹的子集放到一个file类型的数组中 输入及输出的概念 输入input 输出output 把jav…...
睿尔曼超轻量仿人机械臂之复合机器人底盘介绍及接口调用
机器人移动平台是一个包含完整成熟的感知、认知和定位导航能力的轮式机器人底盘产品级平台,产品致力于为各行业细分市场的商用轮式服务机器人提供一站式移动机器人解决方案,让合作伙伴专注在核心业务/人机交互的实现。以下是我司产品双臂机器人以及复合升…...
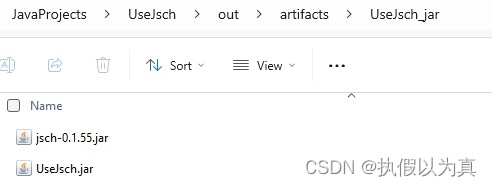
用JSch实现远程传输文件并打包成jar
本文将简单介绍一下 JSch 这个Java的第三方库的一个简单用法,并以此为实例,讲解 IntelliJ 中打包成 jar 包的2种方式。 实现目标 我们的目标是,做出一个jar包,它能够实现类似于 scp 命令的远程传输文件的功能。用法如下…...

2023年第十四届蓝桥杯大赛软件类省赛C/C++研究生组真题(代码完整题解)
C题-翻转⭐ 标签:贪心 简述:如果 S 中存在子串 101 或者 010,就可以将其分别变为 111 和 000,操作可以无限重复。最少翻转多少次可以把 S 变成和 T 一样。 链接: 翻转 思路:要求步骤最少->S每个位置最多修改一次->从头开始遍历不匹配就翻转->翻转不了就-1 …...
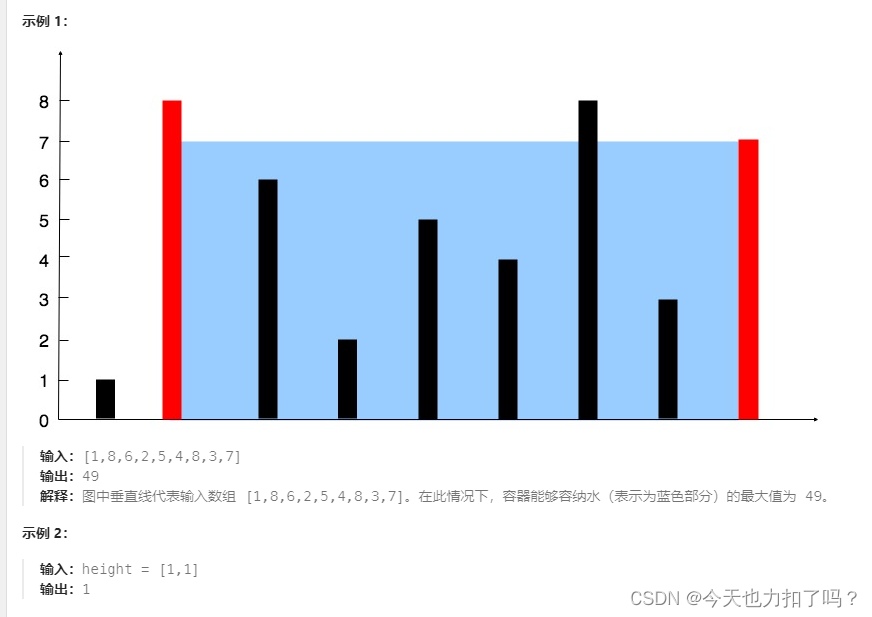
力扣刷题Days28-第二题-11.盛水最多的容器(js)
目录 1,题目 2,代码 3,学习与总结 3.1思路回顾 1,如何遍历 2,算法流程 3.2剖析问题 1,题目 给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, h…...

【笔试真题】- 小红书-2026.03.11
📌 点击直达笔试专栏 👉《大厂笔试突围》 💻 春秋招笔试突围在线OJ 👉 笔试突围在线刷题 bishipass.com 小红书-2026.03.11 本次三题均对应历史原题,红薯已经连续好几场是这样了 题目一:完美数字 这题的关键在于满足条件的连续正整数乘积其实非常少,可以先把所…...

如何从bode图得到单位阶跃的趋势
传递函数>阶跃响应;拉普拉斯逆变化就可以得到时域函数,可以绘制出图像。bode图>阶跃响应;以下例子进行测试:Ge -15.93 s---------------------s^2 16.34 s 94.09从伯德图(Bode Plot)定性判断单位阶…...

LoRA Diffusion生态系统与最佳实践
LoRA Diffusion生态系统与最佳实践 【免费下载链接】lora Using Low-rank adaptation to quickly fine-tune diffusion models. 项目地址: https://gitcode.com/gh_mirrors/lora2/lora LoRA Diffusion项目与HuggingFace Diffusers库的深度集成为用户提供了无缝的模型微调…...

Shodan搜索查询的终极优化策略:基于Awesome Shodan Queries的性能调优指南
Shodan搜索查询的终极优化策略:基于Awesome Shodan Queries的性能调优指南 【免费下载链接】awesome-shodan-queries 🔍 A collection of interesting, funny, and depressing search queries to plug into shodan.io 👩💻 项…...

Facebook iOS SDK 完全指南:5大核心功能快速上手
Facebook iOS SDK 完全指南:5大核心功能快速上手 【免费下载链接】facebook-ios-sdk facebook/facebook-ios-sdk: Facebook iOS SDK 是一套官方提供的 iOS 平台开发工具包,允许开发者将 Facebook 登录、分享、广告等功能集成到自己的 iOS 应用程序中。 …...
使用rpicam-app通过网络流式传输视频)
树莓派超全系列教程文档--(62)使用rpicam-app通过网络流式传输视频
使用rpicam-app通过网络流式传输视频 使用 rpicam-app 通过网络流式传输视频UDPTCPRTSPlibavGStreamerRTPlibcamerasrc GStreamer 元素 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 使用 rpicam-app 通过网络流式传输视频 本节介绍来自 rpica…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
