金钱卦起卦
前言
本文目的:
1.了解什么是《易经》
2.了解什么是八卦/六十四卦
3.金钱卦起卦方法
4.如何解卦
一、什么是易经?
1、易经就是一本书、一本著作
2、它的成书经历了三个阶段
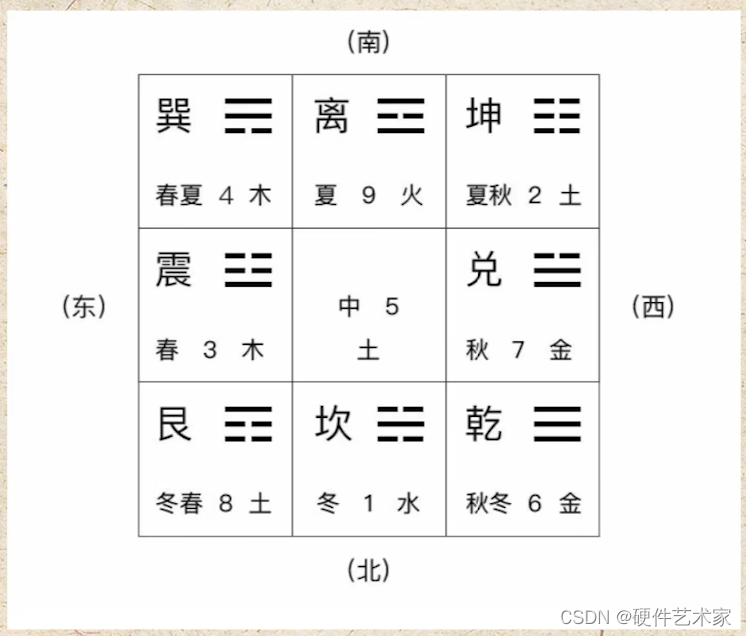
第一阶段:在5000多年前,由人类的始祖伏羲通过观察时间的万事万物、日月山川,画出了八卦图,称为伏羲八卦或先天八卦

第二阶段:由3000多年前的周文王把伏羲八卦改造成了后天八卦,然后还把八卦进行两两之间相互重叠(也就是排列组合),形成了六十四卦
第三阶段:孔子为《易经》做了十篇文章作为注解,称为易传
3、周易和易经有什么区别?
易经:专指周文王所做的六十四卦的部分
周易: 周易=《易经》+《易传》
二、八卦和六十四卦
1、先认识一个字,爻,它代表的就是事件,事件是有不同属性的

2、古人对事件最基本的划分就是阴、阳,阳爻是一条直线,阴爻是两个小段直线
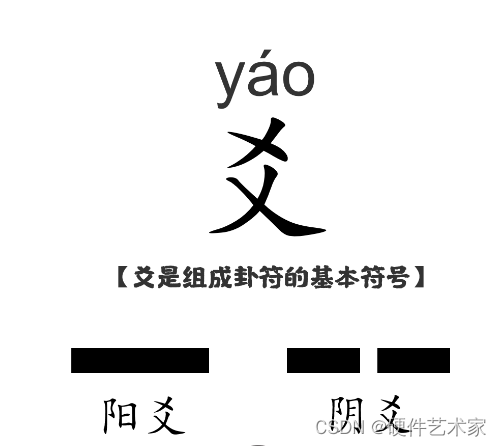
3、每三个爻叠成一个卦,就是八卦,为了记忆八卦卦形,古人编了一首歌谣

4、乾卦,代表天,三个爻都是阳爻,都是连续的直线,故叫做乾三连

5、坤卦,代表地,三个爻都是阴爻,断开成六小段,故叫做坤六段

6、坎卦,代表水,上下为阴,中间为阳,故叫做坎中满

7、离卦,代表火,中间是一条虚线,故叫做离中虚

8、兑卦,代表泽,泽也代表水,但是和坎的水却不一样,坎卦的水是没有驯服的水,是动态的水,是水害;泽是平静的水,是水利。

9、巽卦,代表风,最下面是断开的,是一个阴爻,故称为巽下断。

10、震卦,代表雷,震卦像一个仰放的器皿,因为要盛东西,碗底要实,所以最下面是一条实线,故叫做震仰盂

11、艮卦,代表山,艮卦像一个倒扣的碗,碗底朝上,碗底是实线,故称为艮覆碗

12、八卦符号两两相重,就构成了易经六十四卦,易经的原文讲的就是这六十四卦每一个卦、每一个爻的具体含义
三、爻的命名法
1、卦是从下往上画的,按顺序从下往上叫即可,只需要注意最初的爻和最末的爻分别叫初爻和上爻

2、九为阳,六为阴。爻分阴阳,九代表阳,六代表阴,乾卦均为阳爻,故各个爻里均有九,二到五爻九在前,唯有初爻和上爻九在后。

3、举个既济卦的例子,既济卦中的六四便指的是从下往上数第四个爻,因为它是阴爻,六为阴,故叫六四爻

四、金钱卦起卦方法
1、准备三枚铜钱

2、注意:金钱卦因为较为基础,不能算事情的前因后果,只适用于具体事项的占卜,比如,预测一件事情能不能成、顺不顺利、结果好不好,占卜出来的结果用来参考
3、摇卦步骤;摇卦时,心要静、心里想着问题,只能想一个,不能多,也不能中途变换问题,要点就是心静、心诚

4、摇卦后,三个铜币落下,每个铜币都有正反面,也就是阴面和阳面,铜币哪面为阴哪面为阳有不同说法,个人自己决定,这里以字为阳、花为阴


5、三个铜币可以摇出四种情况
第一种:一阳两阴,取少数,故为阳爻
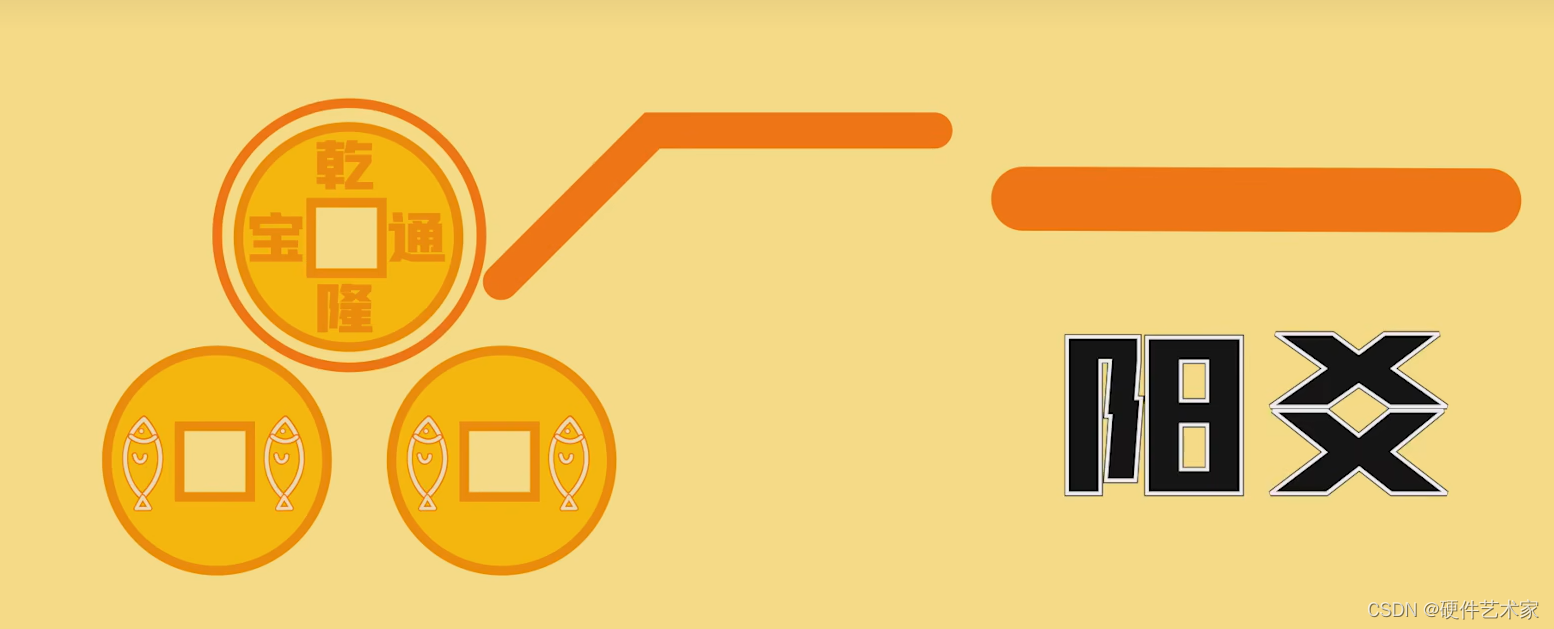
第二种:一阴两阳,取少数,故为阴爻
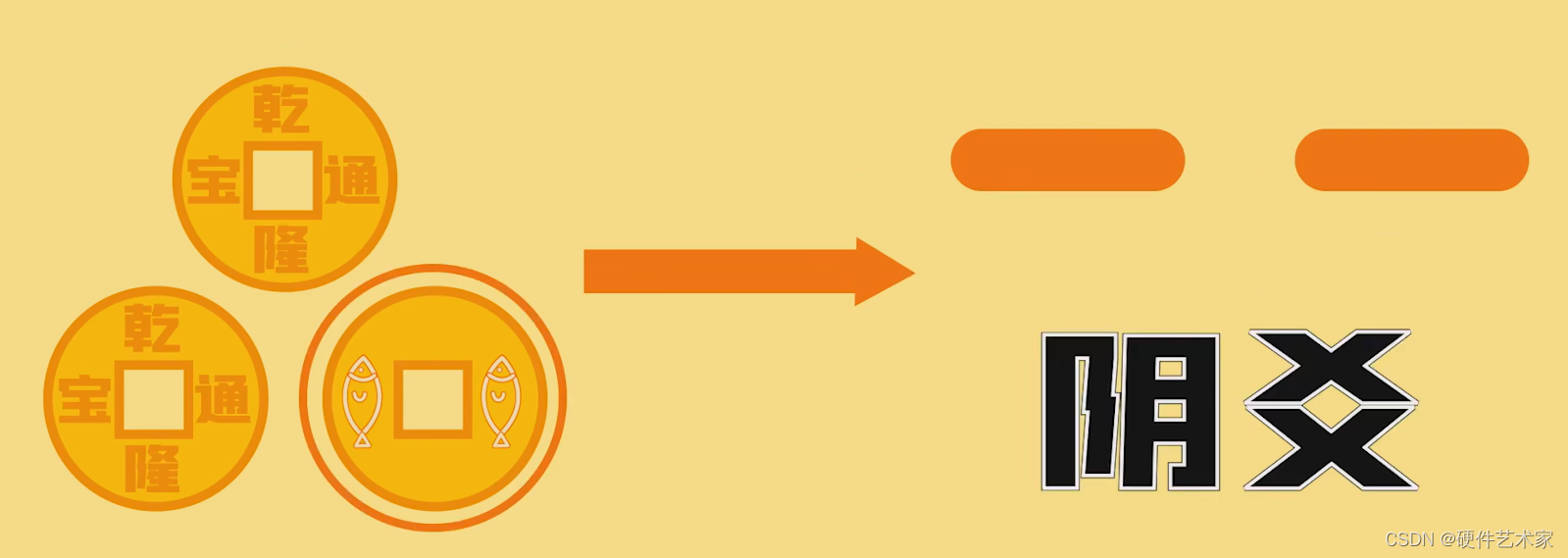
第三种:三阳,称为动阳,在爻旁边画个小三角做区分
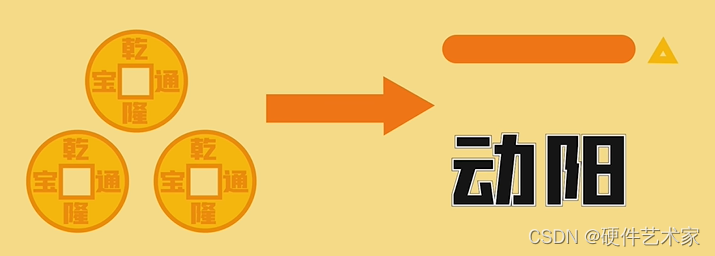
第四种:三阴,称为动阴,在爻旁边画个小三角做区分

6、每摇一次卦,就得到一个爻,摇六次,就得到了六爻卦,动阳和动阴需做区分

五、断卦
1、查六十四卦表,定卦名
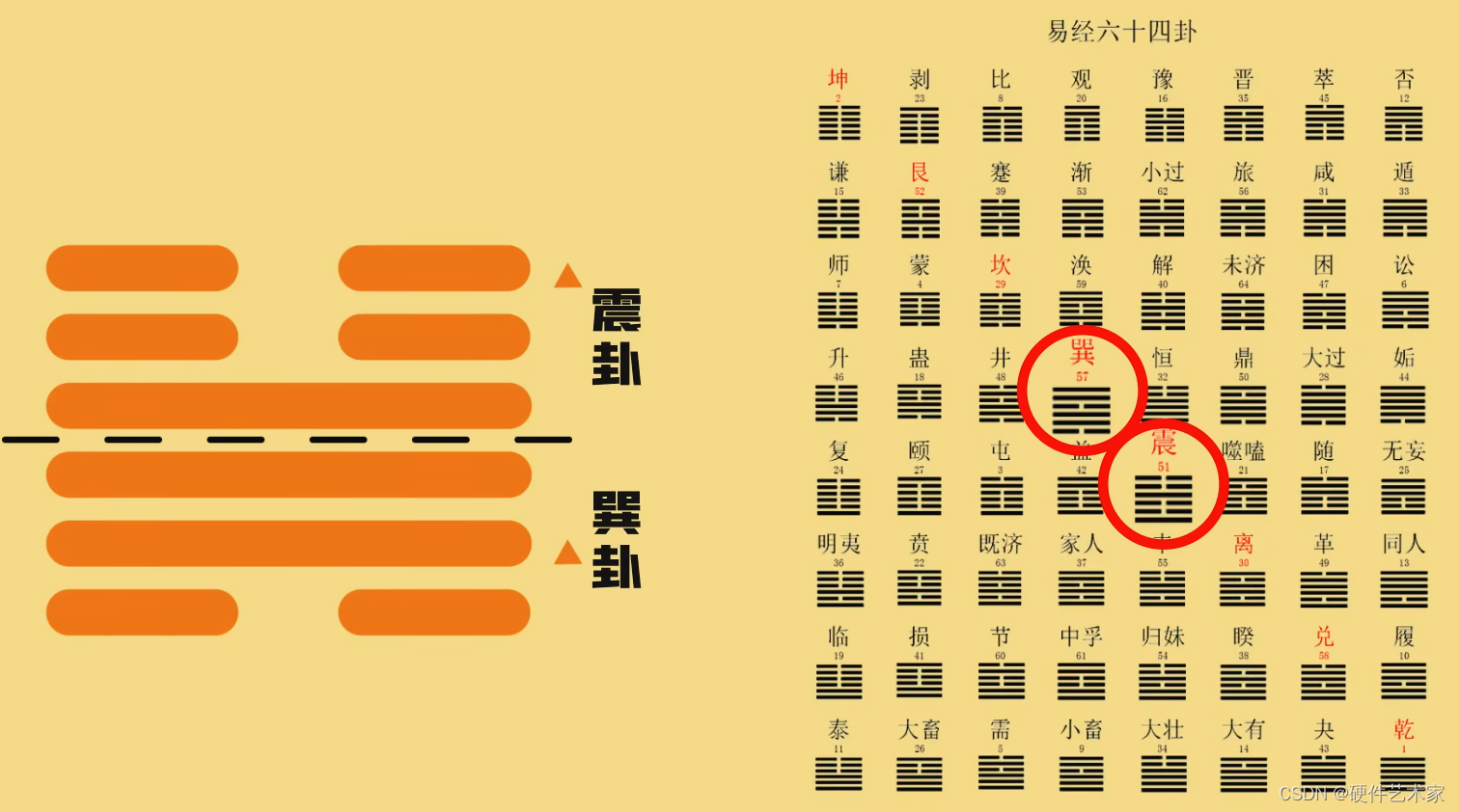
2、查卦名有一种快速的方法,将六爻卦分为上下两部分,上卦画一竖,下卦画一横,就能很快找到卦名


3、还有一种方法确定卦名,根据取象,上卦为震,下卦为巽,震为雷,巽为风,雷风恒,故为恒卦

4、确定了卦名后,开始断卦,卦辞和爻辞查阅周易。六爻中无动爻,以卦辞断之

5、只有一个动爻,以动爻爻辞断之

6、有两个动爻为阴阳两爻,以阴爻爻辞断之

7、两动阳或动阴,取靠上的动爻爻辞断之

8、三个动爻,取中间动爻断之

9、四个动爻,取最下面非动爻断之

10、五个动爻,取非动爻断之

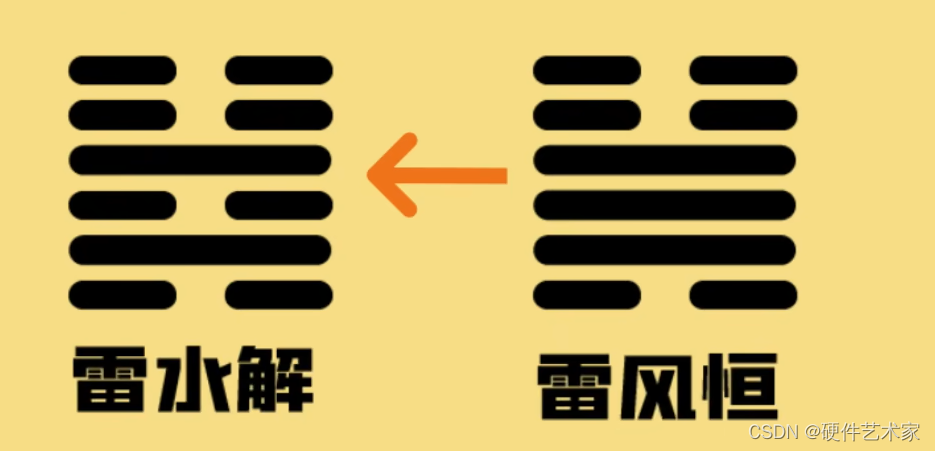
11、六个动爻!!!去八宫图里找这个卦的前一个卦的卦辞来断


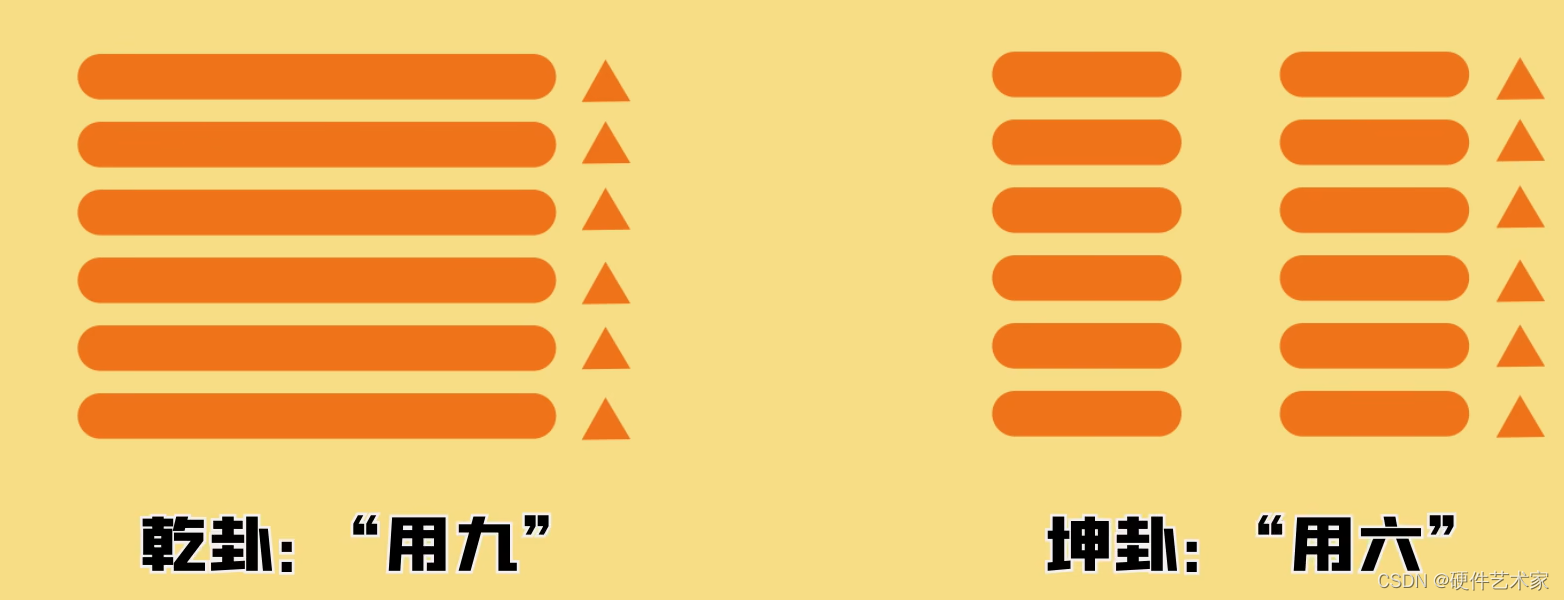
12、六阳或六阴,全是动爻,乾卦用用九断之,坤卦用用六断之
13、汇总

六、最后,
君子居观其象而玩其占,
动则观其变而玩其占,
是以自天佑之,吉无不利。
相关文章:

金钱卦起卦
前言 本文目的: 1.了解什么是《易经》 2.了解什么是八卦/六十四卦 3.金钱卦起卦方法 4.如何解卦 一、什么是易经? 1、易经就是一本书、一本著作 2、它的成书经历了三个阶段 第一阶段:在5000多年前,由人类的始祖伏羲通过观察时…...

学透Spring Boot 003 —— Spring 和 Spring Boot 常用注解(附面试题和思维导图)
这是 学透 Spring Boot 专栏 的第三篇,欢迎关注我,与我一起学习和探讨 Spring Boot 相关知识,学透 Spring Boot。 从面试题说起 今天我们通过一道和Spring Boot有关的常见面试题入手。 面试题:说说 Spring Boot 中有哪些常用注解…...
新能源汽车充电桩常见类型及充电桩站场的智能监管方案
随着新能源汽车市场的迅猛发展,充电桩作为支持其运行的基础设施,也呈现出多样化的类型。这些充电桩不仅在外形和功能上存在差异,更在充电速度、充电方式以及使用场景等方面展现出独特的优势。 一、充电桩类型及区别 1、慢充桩(交…...

让工作自动化起来!无所不能的Python
文章目录 前言一、Python是办公自动化的重要工具二、Python是提升职场竞争力的利器三、Python是企业数字化的重要平台四、Python是AI发展的重要通道之一编辑推荐内容简介作者简介目录前言为什么要写这本书 读者对象如何阅读本书赠书活动 前言 随着我国企业数字化和信息化的深入…...

Facebook轮播广告是什么?投放过程中有哪些需要注意的吗?
轮播广告是Facebook广告形式中的一种,可以把3—5个广告合并到一个可滚动的广告单元中。轮播广告会出现在新鲜事即News Feed中,是独立站卖家常用的一种广告形式 为什么选择轮播广告? 转化率更高:相较于单图广告,轮播广…...
3、jvm基础知识(三)
如何判断堆上的对象没有被引用? 常见的有两种判断方法:引用计数法和可达性分析法。 引用计数法会为每个对象维护一个引用计数器,当对象被引用时加1,取消引用时减1。 引用计数法的优点是实现简单,缺点有两点࿱…...

leetcode414-Third Maximum Number
这道题目求第三大数,如果第三大数不存在则返回最大数,且该数字最大值不超过2^31-1。从这个提示上就可以看出这个数字是用int类型表示的。我们当然可以通过排序的方式先给数组排序然后很容易的就能求解。但是有没有什么更好的办法呢?对于数组来…...
解决Quartus与modelsim联合仿真问题:# Error loading design解决,是tb文件中没加:`timescale 1ns/1ns
解决Quartus与modelsim联合仿真问题:# Error loading design解决,是tb文件中没加:timescale 1,一直走下来,在modelsim中出现了下面问题2,rtl文件、tb文件2.1,rtl代码2.2,tb测试2.3&a…...

vue使用elementui组件的的对话框;使用ref
1.第一步,先在父组件中引用,设置ref的值 <el-dialog :visible.sync"dialogEditVisible"append-to-body width"1000px" title"编辑":close-on-click-modal"false"><dialog-edit v-if"dialogEditV…...

第十四届蓝桥杯(八题C++ 题目+代码+注解)
目录 题目一(日期统计 纯暴力): 代码: 题目二(01串的熵 模拟): 代码: 题目三(治炼金属): 代码: 题目四(飞机降落 深度…...
、请求正文(body))
HTTP协议格式详解之报头(HTTP header)、请求正文(body)
在之前文章中我们已经介绍了HTTP的首行信息,HTTP协议格式详解之首行信息解析-CSDN博客这篇文章中我们继续介绍HTTP协议的报头部分。 一、报头(HTTP header) a)请求头部(Request Headers): Host:指定服务器…...

[yolox]ubuntu上部署yolox的ncnn模型
首先转换pytorch->onnx->param模型,这个过程可以查资料步骤有点多,参考blog.51cto.com/u_15660370/6408303,这里重点讲解转换后部署。 测试环境: ubuntu18.04 opencv3.4.4(编译过程省略,参考我其他博客) 安装…...

YOLOv9改进策略 :IoU优化 | 提出一种新的Shape IoU,更加关注边界框本身的形状和尺度,对小目标检测也很友好
💡💡💡本文改进:一种新的Shape IoU方法,该方法可以通过关注边界框本身的形状和尺度来计算损失,解决边界盒的形状和规模等固有属性对边界盒回归的影响。 💡💡💡对小目标检测涨点明显,在VisDrone2019、PASCAL VOC均有涨点 《YOLOv9魔术师专栏》将从以下各个方向进…...

如何使用KST指标进行多头交易,Anzo Capital一个条件设置
在之前的文章中,我们进行分享了以下知识:什么是KST指标,以及如何进行计算KST指标。有聪明的投资者就在后台进行咨询Anzo Capital昂首资本了,我们知道这些知识有什么用呢? 当然有用了,只要理解背后的逻辑知…...

【QT进阶】第十三章QT动画类的使用QAbstractAnimation
❤️作者主页:凉开水白菜 ❤️作者简介:共同学习,互相监督,热于分享,多加讨论,一起进步! ❤️专栏目录:【零基础学QT】文章导航篇 ❤️专栏资料:https://pan.baidu.com/s/192A28BTIYFHmixRcQwmaHw 提取码:qtqt ❤️点赞 👍 收藏 ⭐再看,养成习惯 订阅的粉丝可通过…...

【机器学习】揭秘无监督学习:机器如何自我学习发现数据奥秘
无监督学习:全面解析 引言 在机器学习的众多分支中,无监督学习因其在未标记数据上发现隐藏模式的能力而独树一帜。它不依赖于事先标记的输出,而是通过分析数据本身的结构和分布来揭示内在的关系和分类。本文深入探讨无监督学习的核心概念、…...
ArkTs语言基础教程(大纲))
鸿蒙(HarmonyOS)ArkTs语言基础教程(大纲)
鸿蒙(HarmonyOS)ArkTs语言基础教程 简介 ArkTS 是鸿蒙生态的应用开发语言。它在保持 TypeScript(简称 TS)基本语法风格的基础上,对 TS 的动态类型特性施加更严格的约束,引入静态类型。同时,提…...
掌握未来商机:如何利用会话式AI赢在起跑线
AI智能助手:提升工作效率的秘密武器 在这个信息爆炸的时代,内容策略成为了品牌与用户之间沟通的重要桥梁。一个有效的内容策略能够帮助品牌提升知名度,建立与目标受众的深度连接,并最终实现转化目标。内容策略不仅涉及内容的创作与…...
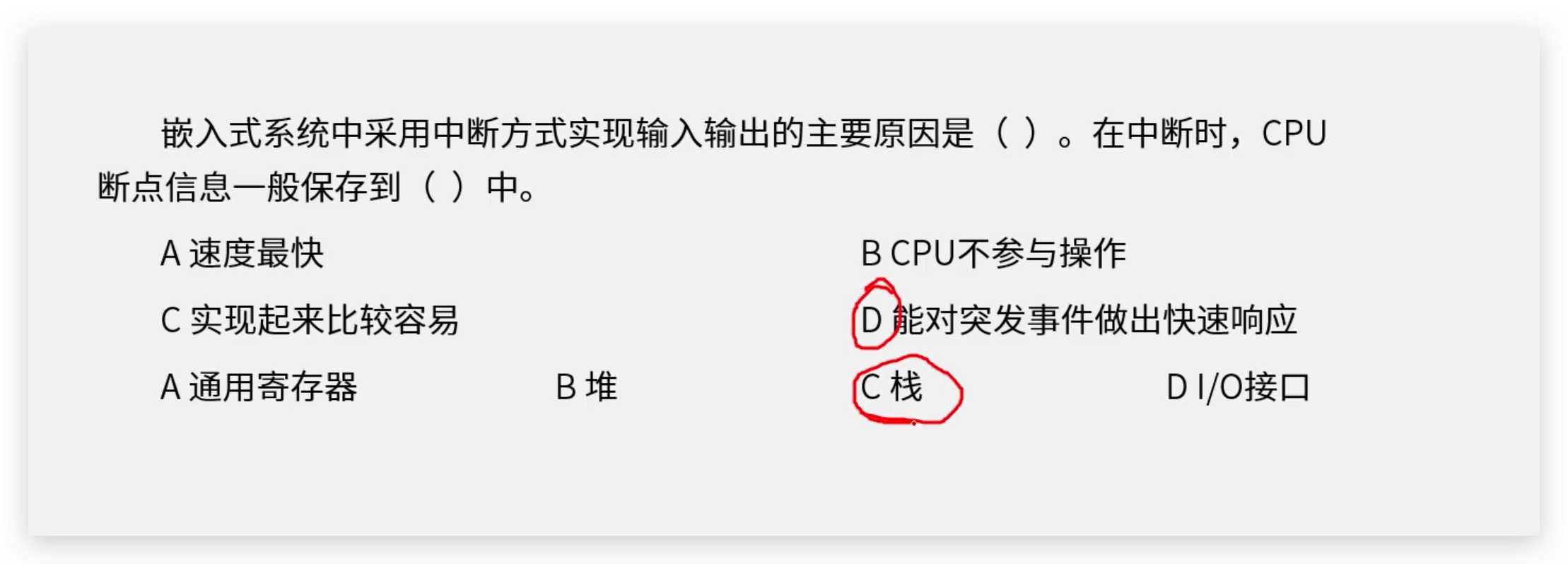
软考高级架构师:数据传输控制方式:程序控制方式、程序中断方式、DMA方式、通道方式、IO处理机
作者:明明如月学长, CSDN 博客专家,大厂高级 Java 工程师,《性能优化方法论》作者、《解锁大厂思维:剖析《阿里巴巴Java开发手册》》、《再学经典:《Effective Java》独家解析》专栏作者。 热门文章推荐&am…...
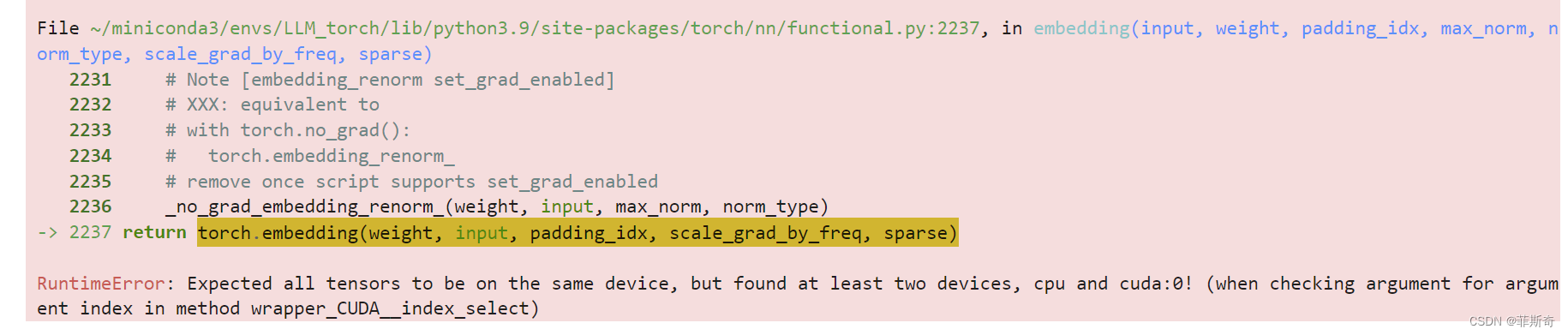
大模型之路2:继续趟一条小路
继续趟一条小路,可谓是充满了曲折,当然,必不可少的还是坑。 吐槽 看过的喷友,其实你看完以后,大概率也就是和我一起骂骂街,因为....我也的确没理清楚。 我也不知道做错了什么,就是运行不过去…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...
