AVL树和红黑树
AVL树和红黑树
- AVL树
- 理论
- 代码实现
- 红黑树
- 理论
- 代码实现
AVL树
理论
我们知道二叉搜索树拥有极高的搜索效率,但当二叉搜索树退化成单支时,其查找效率会大幅下降,因此我们需要避免其出现单支的情况,并且尽可能让其接近满二叉树。解决办法是每次插入一个新结点时,都要保证所有结点的左右子树高度差都不能超过1,倘若新结点插入导致某颗子树左右子树的高度差超过1,就需要进行旋转处理,这样处理后的树称之为AVL树,可以保证其高度不会过高,其查找的时间复杂度的数量级为log(n)。
我们需要在每一个结点中增加一个变量bf以记录该结点的左右子树高度差(称之为平衡因子,一般是用右子树高度减去左子树高度的差作为平衡因子,AVL树中其值只能为-1,0,1)。当我们插入的新结点时,需要对从插入结点到根结点路径上的平衡因子进行调整,调整方法为:左子树高度增加,则当前结点平衡因子减1,右子树高度增加,则当前结点平衡因子加1,接着对其父结点也进行以上操作,直至根结点或者某个祖先结点的平衡因子变为0为止(当前结点平衡因子变为0说明新结点的插入并不影响以当前结点为根的子树的高度,那么自然就不会影响其到根结点路径上的祖先结点的平衡因子)。
倘若调整平衡因子过程中某个结点g的平衡因子变为了-2或者2,则需要进行旋转处理以合理调整树的高度,旋转的情况分为以下4种:
①g的左孩子为p,新插入结点c在p的左子树中
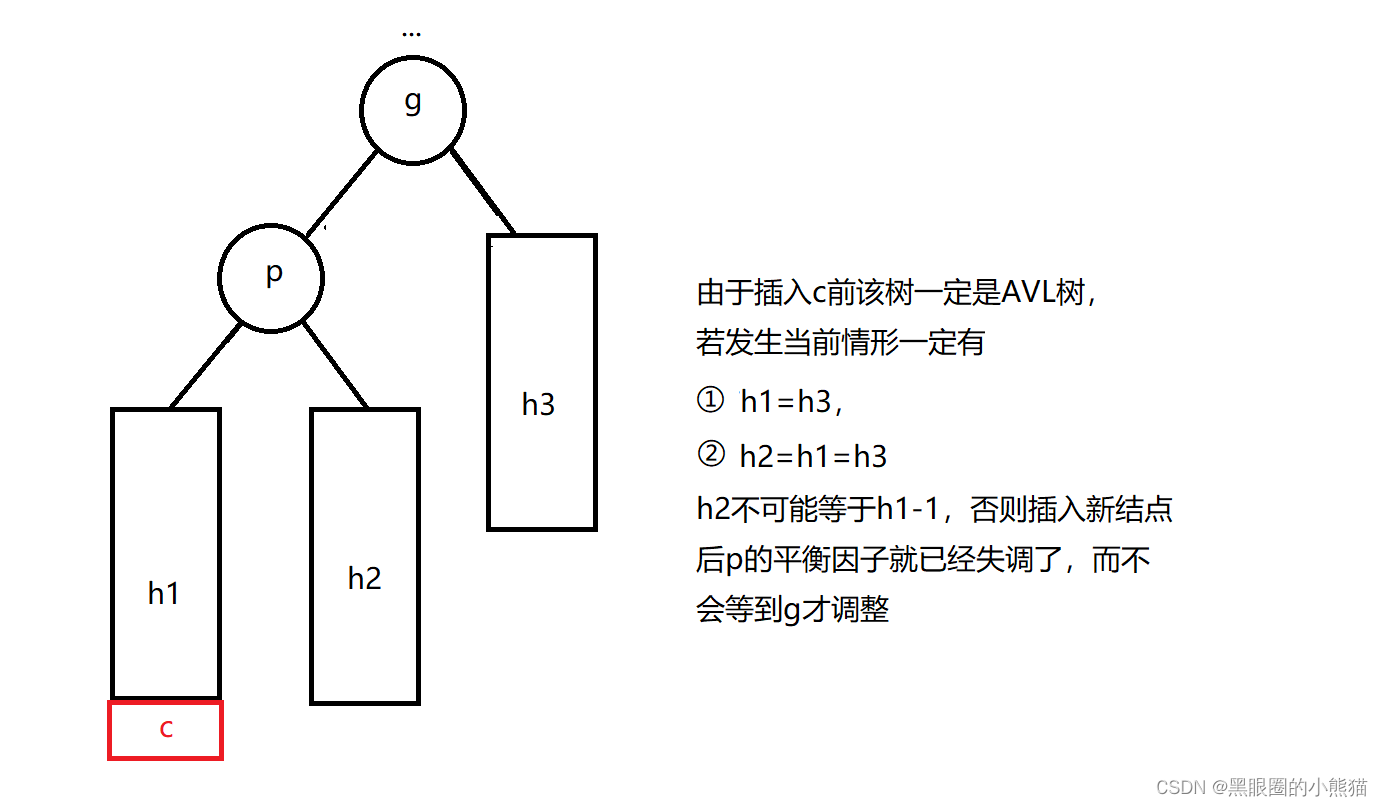
这种情况需要进行以g为根结点进行右单旋,具体步骤为:先将g的左孩子指向改为子树h2,h2子树的根结点的父亲指向改为指向g(如果子树h2存在的话),接着将p的左孩子指向改为指向g,p的父亲指向改为指向g指向的父结点,最后将g的父亲结点指向g的孩子指向改为指向p(如果g的父亲结点存在的话),g的父亲指向改为指向p。
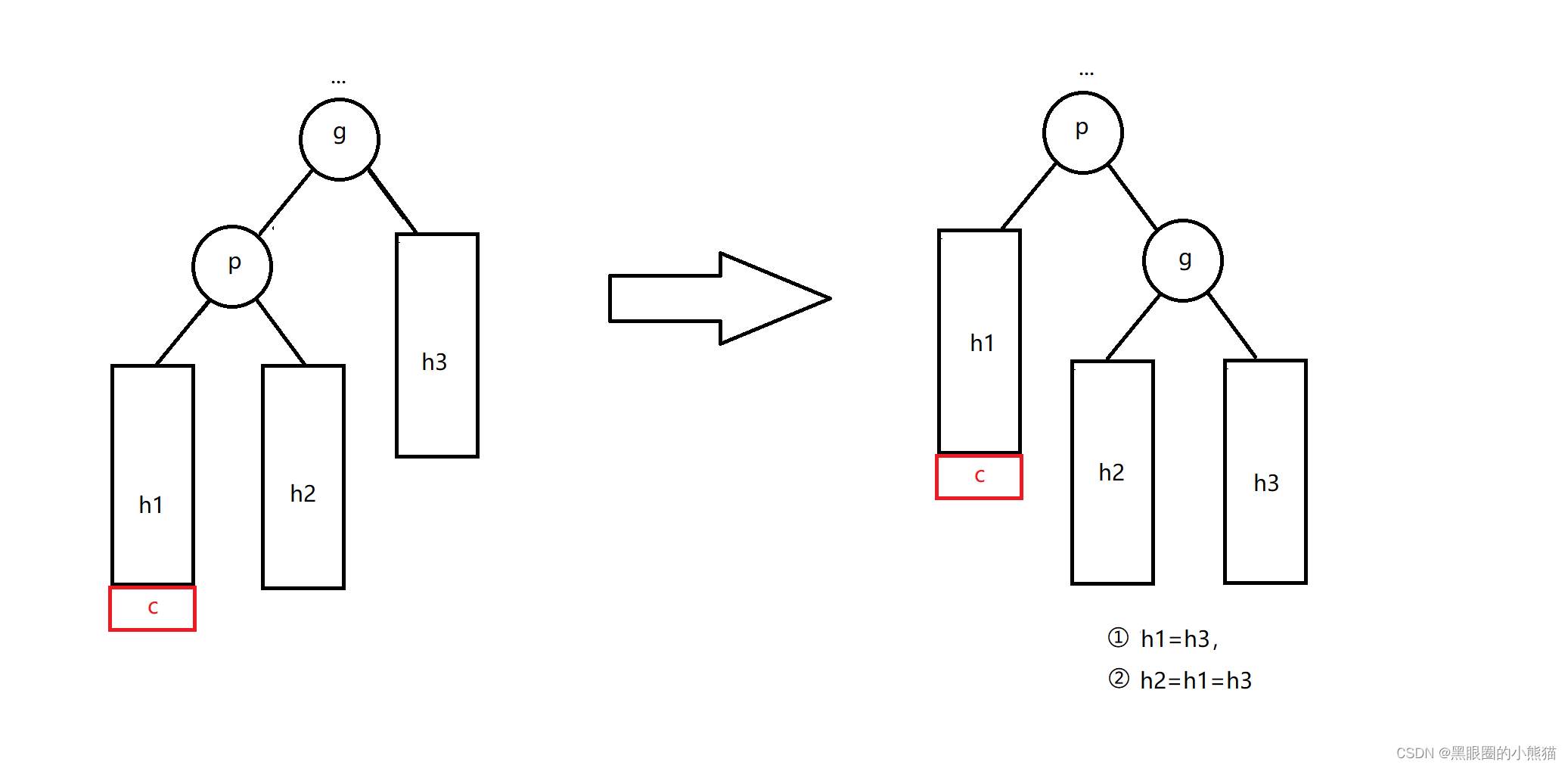
此时p的平衡因子必定为0,调整后以p为根结点的子树的高度与插入结点前以g为根结点的子树高度相比并无变化,因此从p结点到根结点路径上面的祖先结点的平衡因子不需要再进行调整。
②g的右孩子为p,新插入结点c在p的右子树中
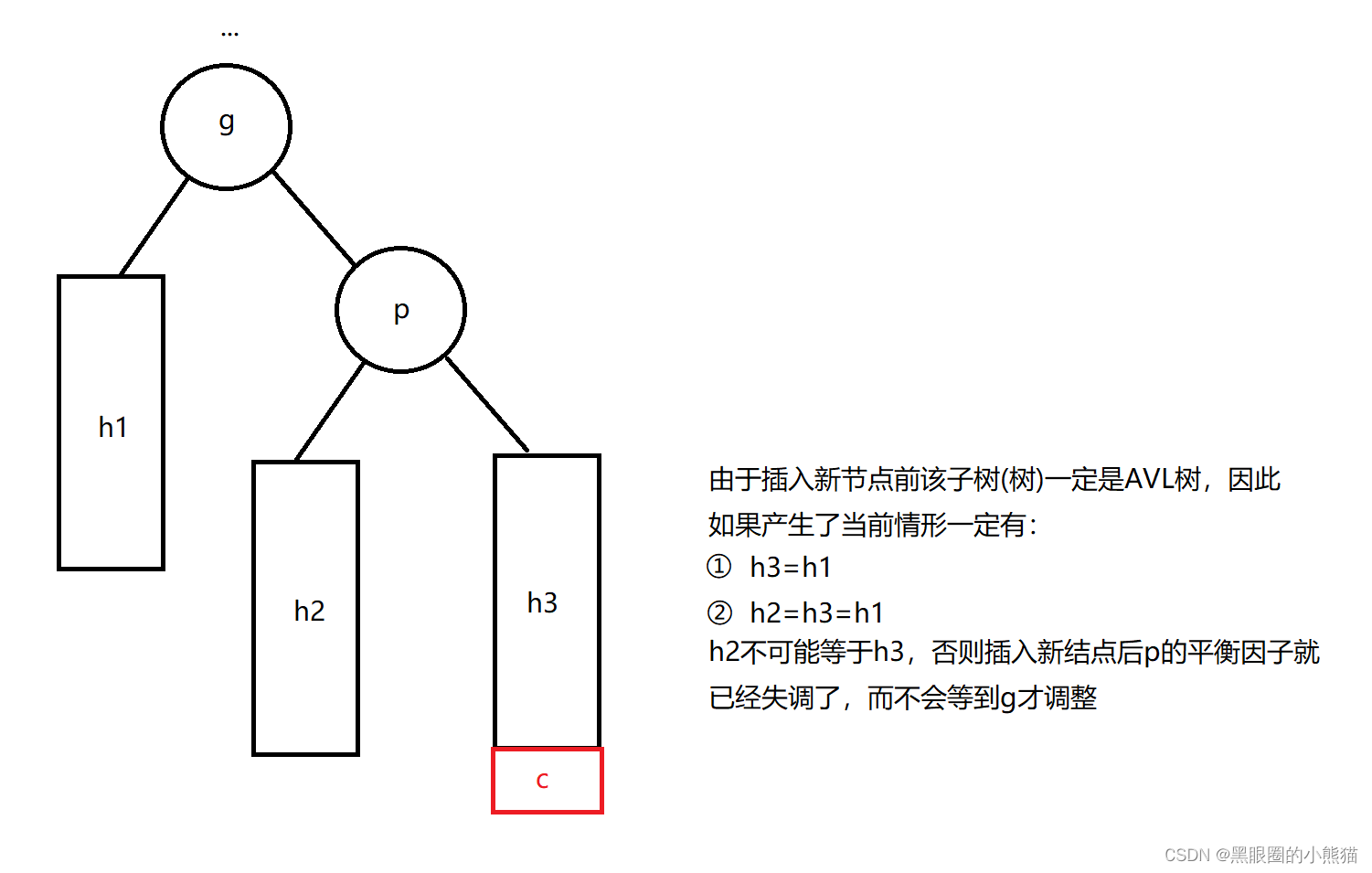
这种情况我们需要以g为根结点进行左单旋,具体步骤为:先将g的右孩子指向改为指向子树h2,再将h2的根结点的父亲指向改为指向g(如果子树h2不为空),接着将p的左孩子指向改为指向g,p的父亲指向改为指向g指向的父亲结点,最后将的父结点指向g的孩子指向改为指向p,g的父亲指向改为指向p。
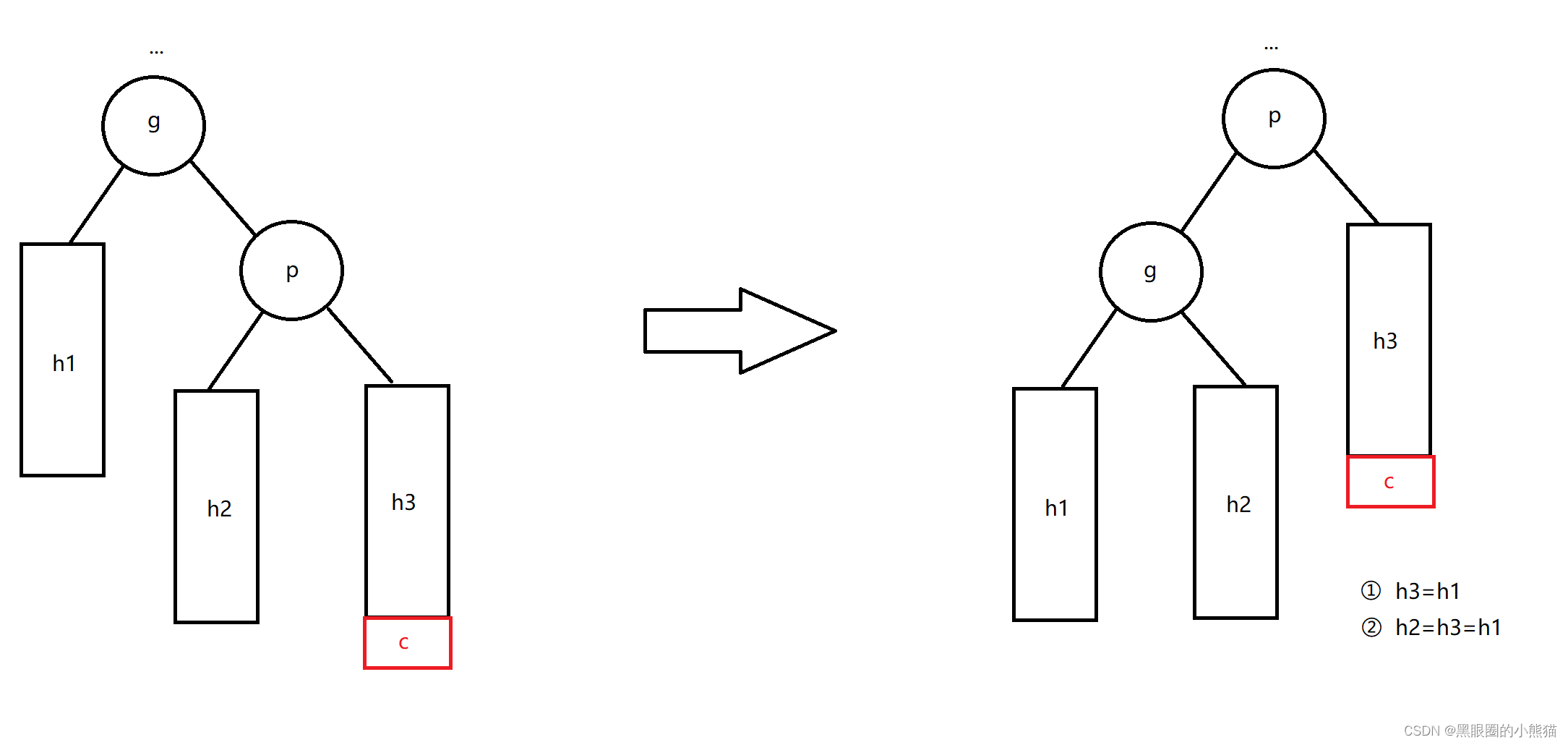
此时p的平衡因子也必定为0,调整后以p为根结点的子树的高度与插入结点前以g为根结点的子树高度相比也无变化,因此从p结点到根结点路径上面的祖先结点的平衡因子也不需要再进行调整。
③g的左孩子为p,新插入结点c在p的右子树中
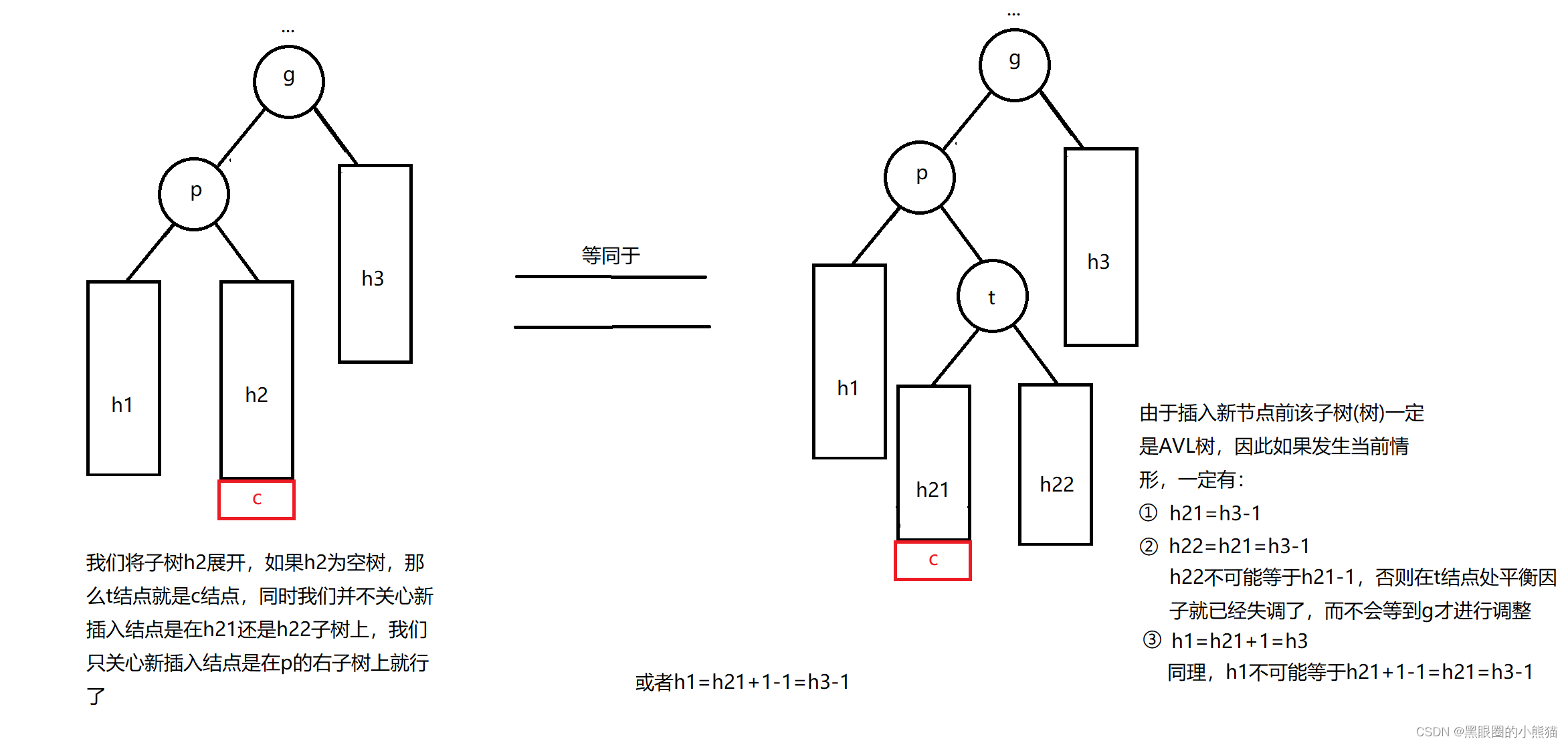
这种情况我们需要进行左右双旋,具体做法为:
1.以p结点为根结点进行左单旋
2.以g结点为根结点进行右单旋
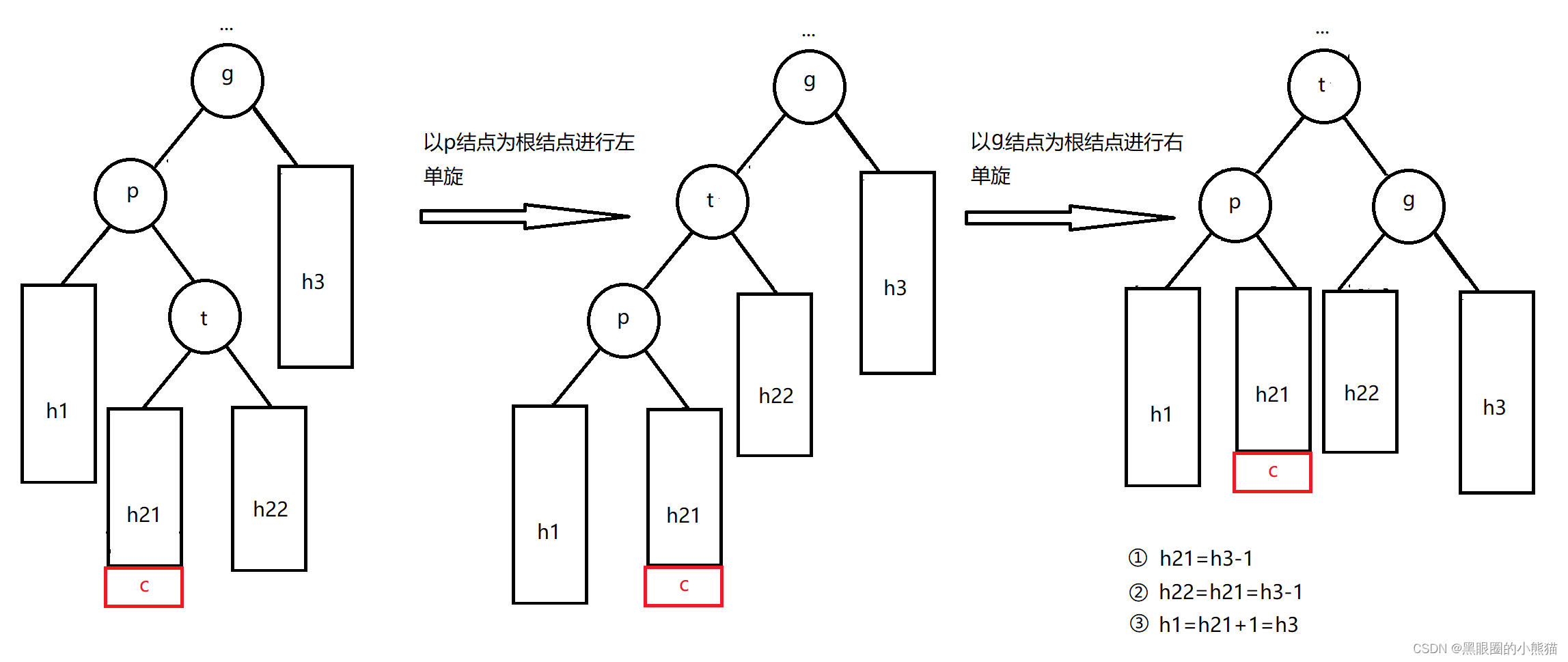
此时结点t的平衡因子也必定为0,调整后以p为根结点的子树的高度与插入结点前以g为根结点的子树高度相比并无变化,因此从p结点到根结点路径上面的祖先结点的平衡因子不需要再进行调整。
④g的右孩子为p,新插入结点c在p的左子树中
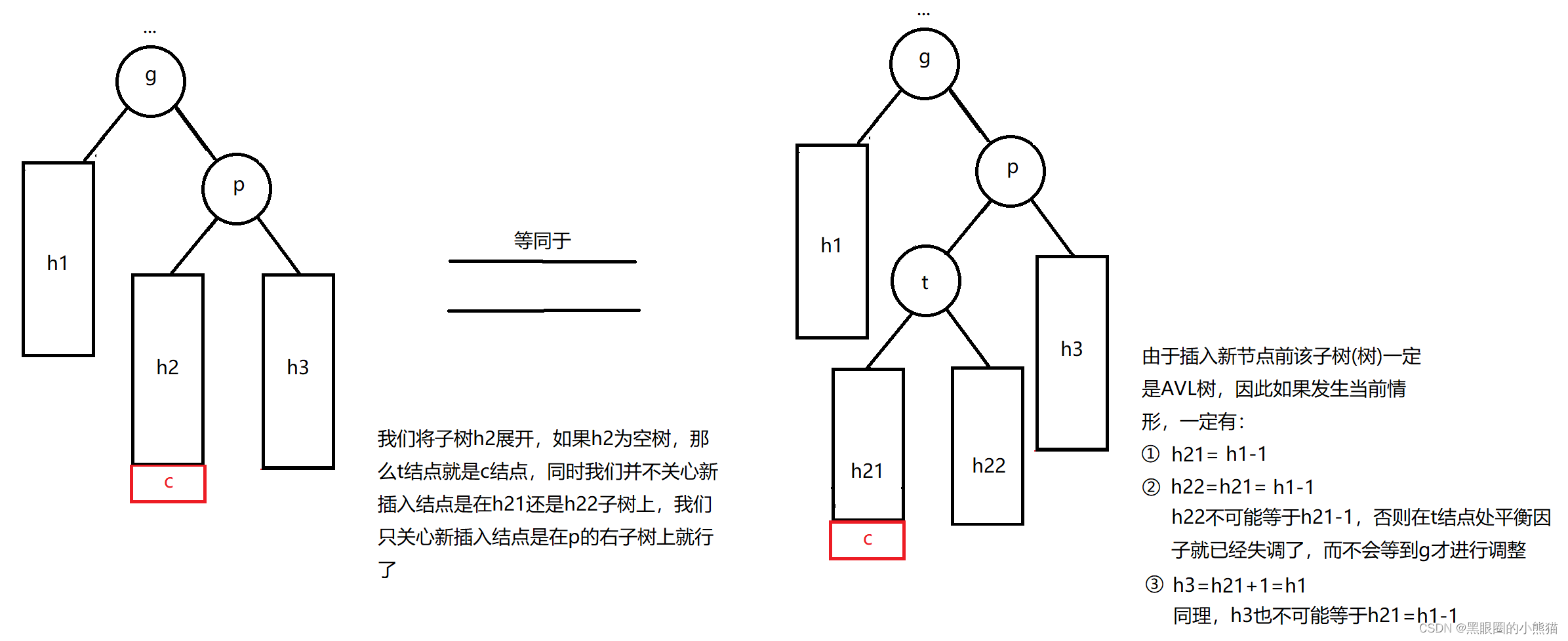
这种情况我们需要进行右左双旋,具体做法为:
1.以p结点为根结点进行右单旋
2.以g结点为根结点进行左单旋
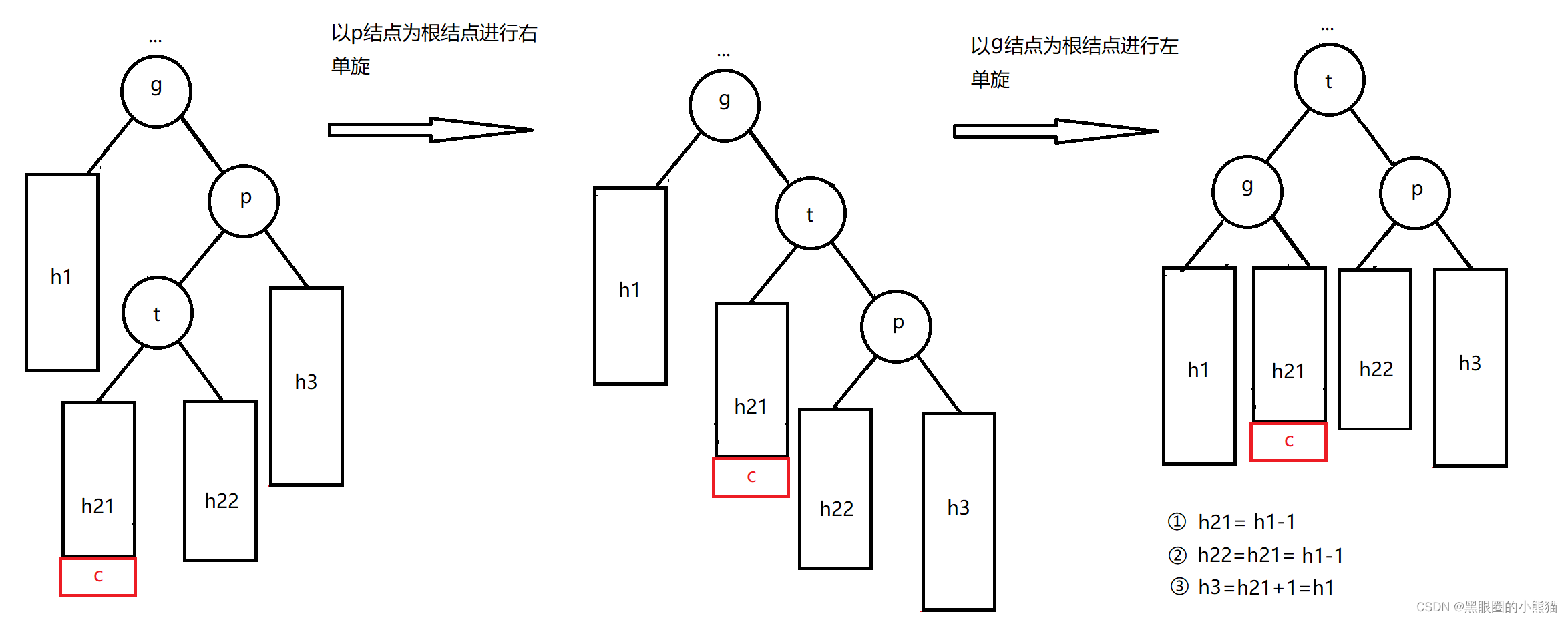
此时结点t的平衡因子也必定为0,调整后以p为根结点的子树的高度与插入结点前以g为根结点的子树高度相比并无变化,因此从p结点到根结点路径上面的祖先结点的平衡因子不需要再进行调整。
AVL树结点的删除我们不进行讨论,可以知道其结点的删除最坏情况下需要进行树的高度次的旋转,因此AVL树适用于数据是静态的情况,如果结构需要经常修改,AVL树就不太适用了。
代码实现
template<class T>
struct AVLTreeNode
{AVLTreeNode(const T& data = T()): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _bf(0){}AVLTreeNode<T>* _left;AVLTreeNode<T>* _right;AVLTreeNode<T>* _parent;T _data;int _bf; // 节点的平衡因子
};template<class T>
class AVLTree
{typedef AVLTreeNode<T> Node;
public:AVLTree(): _root(nullptr){}// 在AVL树中插入值为data的节点bool Insert(const T& data){Node* cur = new Node(data);if (nullptr == _root){_root = cur;return true;}Node* tmp = _root;Node* parent = nullptr;//插入while (tmp){parent = tmp;if (cur->_data > tmp->_data){tmp = tmp->_right;}else if (cur->_data < tmp->_data){tmp = tmp->_left;}else{return false;}}if (cur->_data > parent->_data){parent->_right = cur;cur->_parent = parent;}else{parent->_left = cur;cur->_parent = parent;}//调整平衡因子parent = cur;Node* grandpa = parent->_parent;while (grandpa){if (parent == grandpa->_left){--grandpa->_bf;}else{++grandpa->_bf;}if (2 == grandpa->_bf || -2 == grandpa->_bf)//旋转{if (parent == grandpa->_left && cur == parent->_left){//右单旋RotateR(grandpa);}else if (parent == grandpa->_right && cur == parent->_right){//左单旋RotateL(grandpa);}else if (parent == grandpa->_left && cur == parent->_right){//左右双旋RotateLR(grandpa);}else if (parent == grandpa->_right && cur == parent->_left){//右左双旋RotateRL(grandpa);}break;}else if (0 == grandpa->_bf){break;}cur = parent;parent = grandpa;grandpa = grandpa->_parent;}return true;}private:// 右单旋void RotateR(Node* parent){Node* left_child = parent->_left;parent->_left = left_child->_right;if (left_child->_right){left_child->_right->_parent = parent;}left_child->_right = parent;left_child->_parent = parent->_parent;if (parent->_parent){if (parent->_parent->_left == parent){//parent为其父结点的左孩子parent->_parent->_left = left_child;}else{//parent为其父结点的右孩子parent->_parent->_right = left_child;}}parent->_parent = left_child;if (_root == parent){_root = left_child;}//调整平衡因子left_child->_bf = 0;parent->_bf = 0;}// 左单旋void RotateL(Node* parent){Node* right_child = parent->_right;parent->_right = right_child->_left;if (right_child->_left){right_child->_left->_parent = parent;}right_child->_left = parent;right_child->_parent = parent->_parent;if (parent->_parent){if (parent->_parent->_left == parent){//parent为其父结点的左孩子parent->_parent->_left = right_child;}else{//parent为其父结点的右孩子parent->_parent->_right = right_child;}}parent->_parent = right_child;if (_root == parent){_root = right_child;}//调整平衡因子right_child->_bf = 0;parent->_bf = 0;}// 左右双旋void RotateLR(Node* parent){int pLR_bf = parent->_left->_right->_bf;RotateL(parent->_left);RotateR(parent);//调整平衡因子if (1 == pLR_bf){parent->_bf = 0;parent->_parent->_bf = 0;parent->_parent->_left->_bf = -1;}else if (-1 == pLR_bf){parent->_bf = 1;parent->_parent->_bf = 0;parent->_parent->_left->_bf = 0;}else if (0 == pLR_bf){parent->_bf = 0;parent->_parent->_bf = 0;parent->_parent->_left->_bf = 0;}}// 右左双旋void RotateRL(Node* parent){int pLR_bf = parent->_right->_left->_bf;RotateR(parent->_right);RotateL(parent);//调整平衡因子if (1 == pLR_bf){parent->_bf = -1;parent->_parent->_bf = 0;parent->_parent->_right->_bf = 0;}else if (-1 == pLR_bf){parent->_bf = 0;parent->_parent->_bf = 0;parent->_parent->_right->_bf = 1;}else if (0 == pLR_bf){parent->_bf = 0;parent->_parent->_bf = 0;parent->_parent->_right->_bf = 0;}}private:Node* _root;
};
红黑树
理论
红黑树通过颜色来控制树的高度,可以保证树的最大高度不会超过最小高度的2倍,其结点的颜色由以下规则来约束:
1.每个结点不是红色就是黑色
2.空节点可以看做是黑色结点
3.根结点是黑色的
4.一条路径上不能存在连续的红色结点(即如果当前结点是红色结点,那么其父亲结点和左右孩子结点必定是黑色的)
5.从根结点到叶子结点的每条路径上的黑色结点个数相同
由以上规则可知,红黑树的最小高度路径是该路径上的所有结点都是黑色的,最大高度路径是该路径上黑色和红色结点交替出现,这样就可以保证树的最大高度不会超过最小高度的2倍。
因此,只要遵循以上规则,红黑树的高度就可以保证。
我们需要在每个结点中增加一个变量color记录当前结点的颜色,在进行插入时,新插入的结点的颜色是红色,如果新插入结点的父结点的颜色是黑色的,则红黑树不需要进行任何调整,否则就需要调整。用c表示当前结点,p表示c的父亲结点,g表示c的祖父结点,u表示c的叔叔结点,其需要进行调整情况可以粗分为以下2种(细分5种):
-
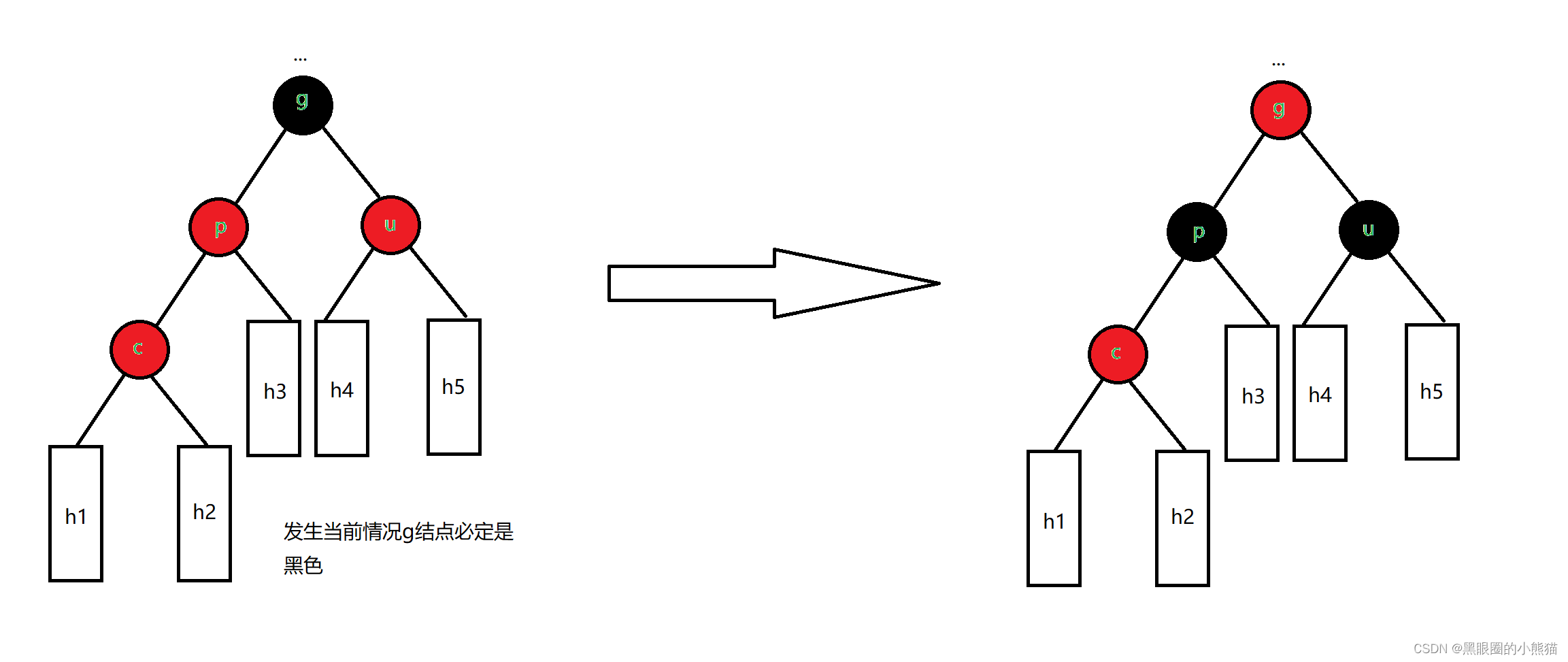
u存在且为红色结点
我们只需要将p结点和u结点改为黑色,g改为红色,那么就可保证以g为根结点的子树必定遵循以上规则,接着将g赋给c,然后继续往上更新调整,直至不再出现连续红色结点或到根结点为止,如果更新到了根结点,我们最后必须让根结点变为黑色。
-
u为空结点或u为黑色结点
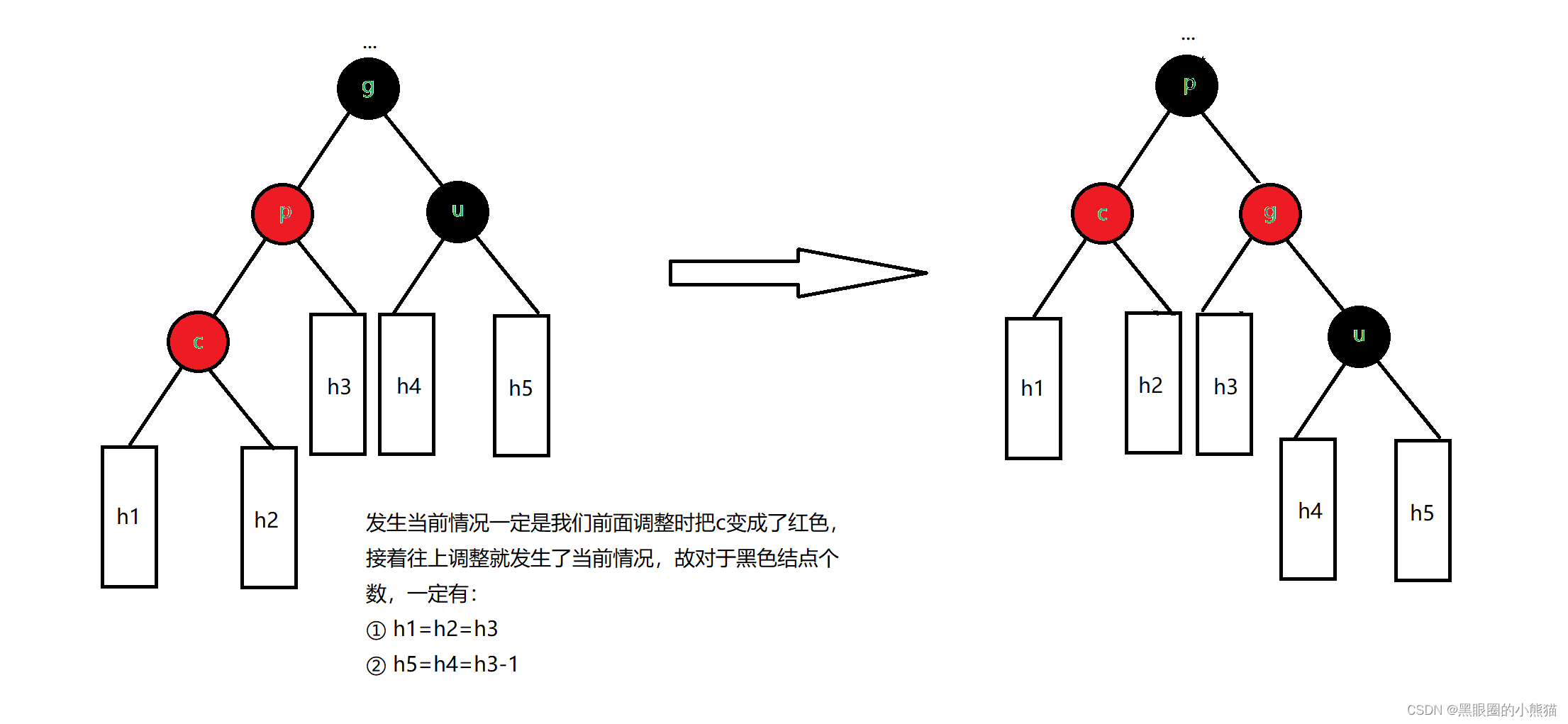
①c是p的左孩子,p是g左孩子
我们只需要以g为根结点进行一次右单旋,然后将p结点改成黑色,g结点改成红色,就一定可以保证整棵树依旧是红黑树,不必再往上调整。
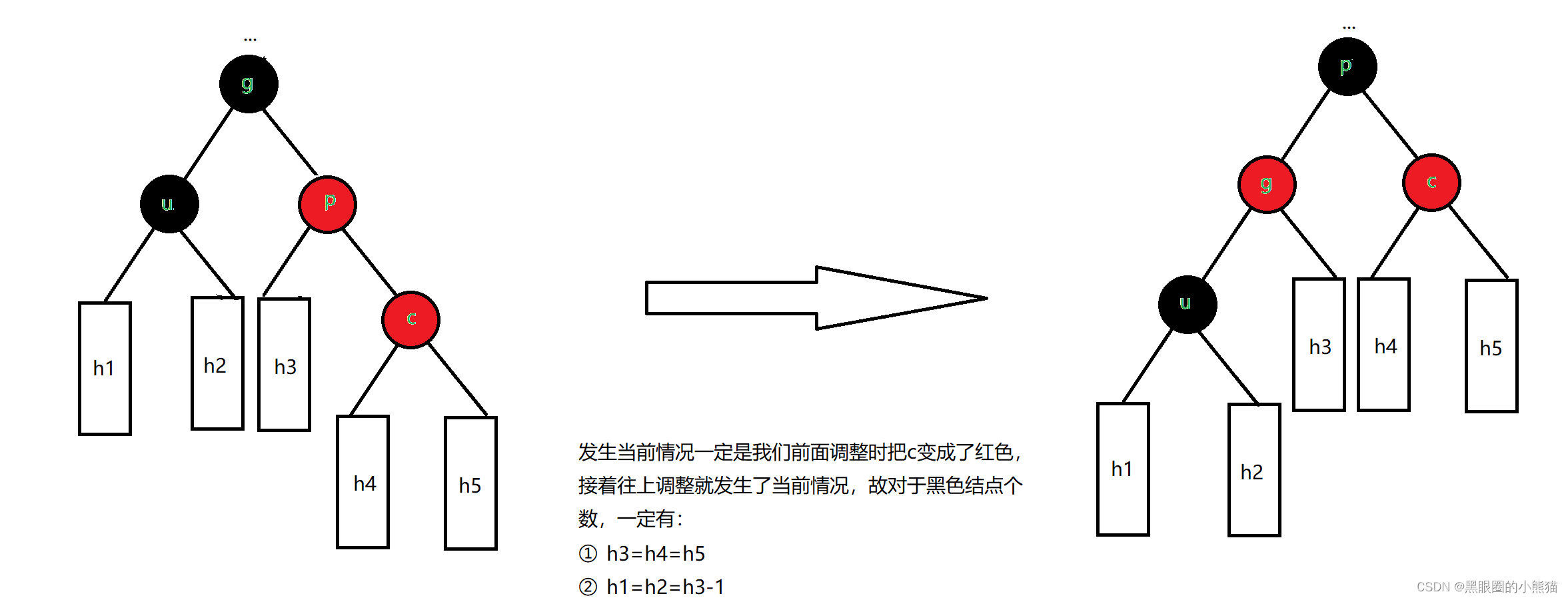
②c是p的右孩子,p是g右孩子
我们只需要以g为根结点进行一次左单旋,然后将p结点改成黑色,g结点改成红色,就一定可以保证整棵树依旧是红黑树,不必再往上调整。
③c是p的右孩子,p是g左孩子
我们只需要以p为根结点进行一次左单旋,然后以g为根结点进行一次右单旋,再将c结点改成黑色,g结点改成红色,就一定可以保证整棵树依旧是红黑树,不必再往上调整。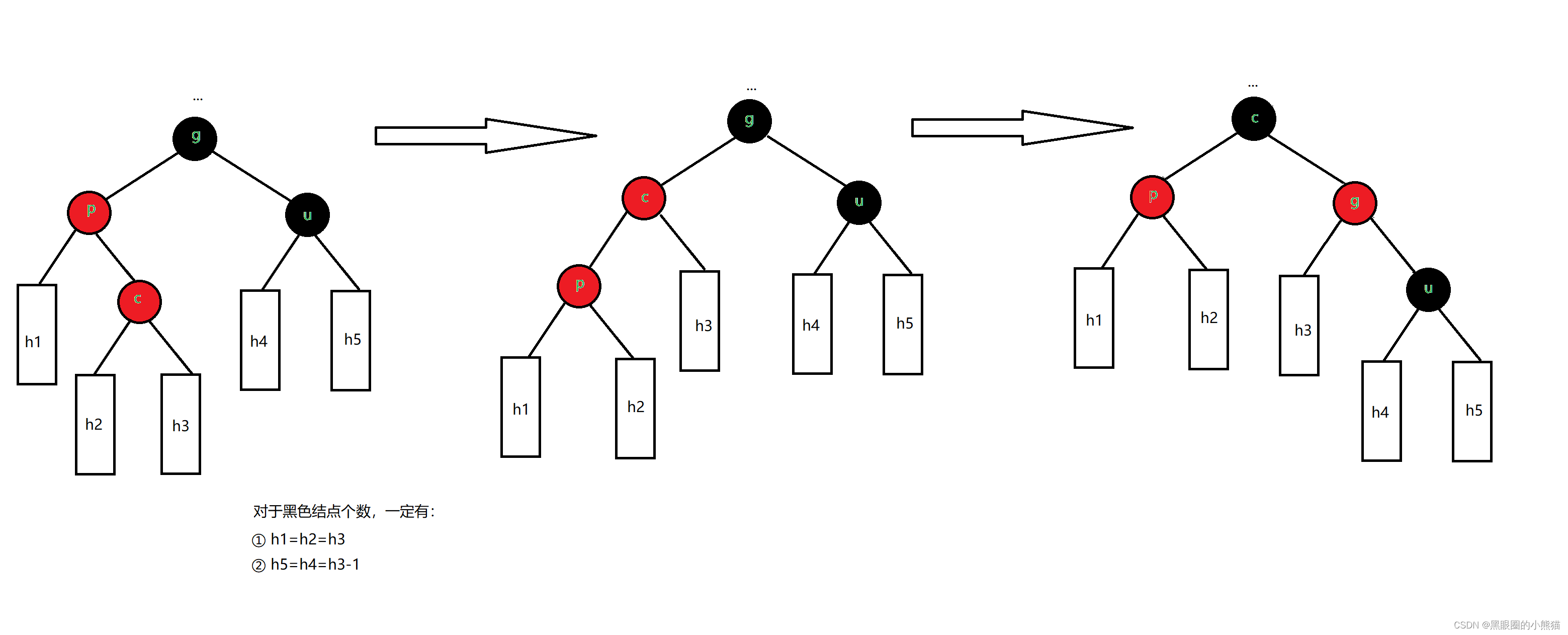
④c是p的左孩子,p是g右孩子
我们只需要以p为根结点进行一次右单旋,然后以g为根结点进行一次左单旋,再将c结点改成黑色,g结点改成红色,就一定可以保证整棵树依旧是红黑树,不必再往上调整。
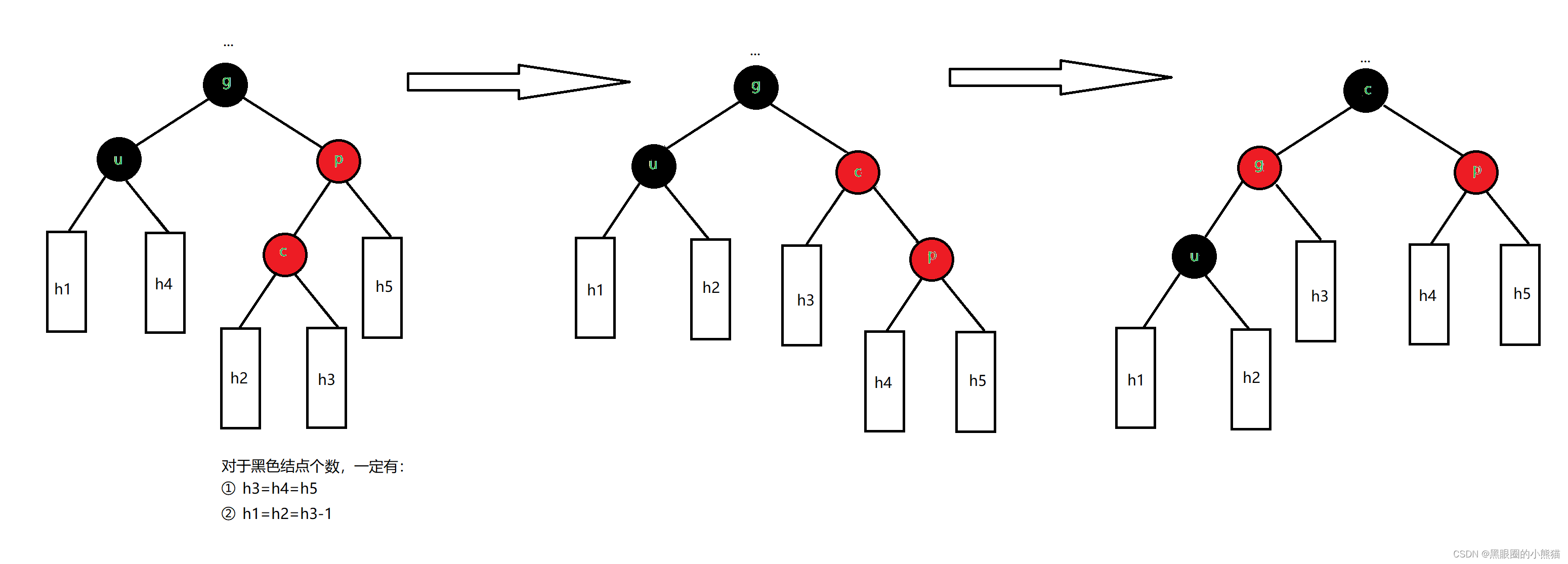
红黑树结点的删除这里也不进行讨论。尽管红黑树的高度比AVL树高,但其在查找过程中性能与AVL树在同一个数量级上,为log(n),且相比较于AVL树,红黑树降低了插入删除时旋转的次数,因此在经常增删的结构中红黑树的性能更优一点。
代码实现
enum Color
{red,black
};template<class T>
struct RBTreeNode
{RBTreeNode(const T& data = T()): _left(nullptr), _right(nullptr), _parent(nullptr), _data(data), _color(red){}RBTreeNode<T>* _left;RBTreeNode<T>* _right;RBTreeNode<T>* _parent;T _data;Color _color; // 节点颜色
};template<class T>
class RBTree
{typedef RBTreeNode<T> Node;
public:RBTree():_root(nullptr){}// 注意:为了简单起见,实现的红黑树不存储重复性元素bool Insert(const T& data){//节点插入Node* newNode = new Node(data);if (_root == nullptr){_root = newNode;return true;}Node* cur = _root;while (cur){if (data > cur->_data && cur->_right){cur = cur->_right;}else if (data < cur->_data && cur->_left){cur = cur->_left;}else if (data == cur->_data){return false;}else{break;}}if (data > cur->_data){cur->_right = newNode;}else{cur->_left = newNode;}newNode->_parent = cur;//节点调整Node* grandpa =cur->_parent;Node* parent = cur;cur = newNode;while (nullptr!=grandpa){if (black == parent->_color){//cur节点的父节点为黑色,无需调整return true;}Node* uncle = grandpa->_right;if (parent == uncle){uncle = grandpa->_left;}if (uncle && red == uncle->_color){//叔叔节点存在且为红色uncle->_color = black;parent->_color = black;grandpa->_color = red;cur = grandpa;if (cur == _root){//如若cur已经是根节点,要将其修改为黑色cur->_color = black;break;}}else{//叔叔节点不存在或者叔叔节点为黑色if (parent == grandpa->_left && cur == parent->_left){//右单旋RotateR(grandpa);}else if (parent == grandpa->_right && cur == parent->_right){//左单旋RotateL(grandpa);}else if (parent == grandpa->_left && cur == parent->_right){//左右双旋RotateLR(grandpa);}else if (parent == grandpa->_right && cur == parent->_left){//右左双旋RotateRL(grandpa);}else{cout << "节点插入出错" << endl;exit(-1);}break;}parent = cur->_parent;grandpa = parent->_parent;}}private:// 左单旋void RotateL(Node* grandpa){//调整节点颜色grandpa->_color = red;grandpa->_right->_color = black;//节点旋转Node* right_child = grandpa->_right;grandpa->_right = right_child->_left;if (right_child->_left){right_child->_left->_parent = grandpa;}right_child->_left = grandpa;right_child->_parent = grandpa->_parent;if (grandpa->_parent){if (grandpa->_parent->_left == grandpa){//parent为其父结点的左孩子grandpa->_parent->_left = right_child;}else{//parent为其父结点的右孩子grandpa->_parent->_right = right_child;}}grandpa->_parent = right_child;if (_root == grandpa){_root = right_child;}}// 右单旋void RotateR(Node* grandpa){//调整节点颜色grandpa->_color = red;grandpa->_left->_color = black;//旋转节点Node* left_child = grandpa->_left;grandpa->_left = left_child->_right;if (left_child->_right){left_child->_right->_parent = grandpa;}left_child->_right = grandpa;left_child->_parent = grandpa->_parent;if (grandpa->_parent){if (grandpa->_parent->_left == grandpa){//grandpa为其父结点的左孩子grandpa->_parent->_left = left_child;}else{//grandpa为其父结点的右孩子grandpa->_parent->_right = left_child;}}grandpa->_parent = left_child;if (_root == grandpa){_root = left_child;}}//左右双旋void RotateLR(Node* grandpa){//调整节点颜色grandpa->_color = red;grandpa->_left->_right->_color = black;//旋转RotateL(grandpa->_left);RotateR(grandpa);}//右左双旋void RotateRL(Node* grandpa){//调整节点颜色grandpa->_color = red;grandpa->_right->_left->_color = black;//旋转RotateR(grandpa->_right);RotateL(grandpa);}private:Node* _root;
};
相关文章:

AVL树和红黑树
AVL树和红黑树 AVL树理论代码实现 红黑树理论代码实现 AVL树 理论 我们知道二叉搜索树拥有极高的搜索效率,但当二叉搜索树退化成单支时,其查找效率会大幅下降,因此我们需要避免其出现单支的情况,并且尽可能让其接近满二叉树。解…...

多线程入门
多线程 Thread 现在的Thread中的run方法,已经被实现了,所以已经不需要实现了 操作 继承 extends Thread方法 重写run方法 start() 案例 public class ThreadTest extends Thread{public void run() {for (int i 0; i < 100; i) {System.out.…...

#!/bin/sh和#!/bin/bash的区别
前言:都是脚本文件中的 shebang(也称为 hashbang)行,用于指定脚本文件的解释器 解释: #!/bin/sh:这行告诉操作系统使用 /bin/sh 这个解释器来执行脚本。/bin/sh 是一个标准的 Unix Shell,通常是…...
腾讯云(CVM)托管进行权限维持
前言 刚好看到一个师傅分享了一个阿里云ECS实战攻防,然后想到了同样利用腾讯云CVM的托管亦可实现在实战攻防中的权限维持。 简介 腾讯云自动化助手(TencentCloud Automation Tools,TAT)是一个原生运维部署工具,它可…...
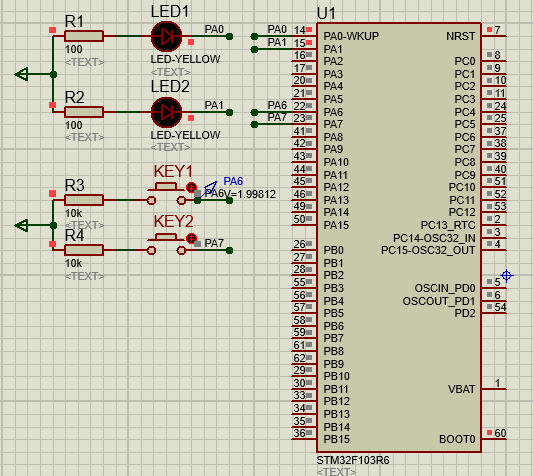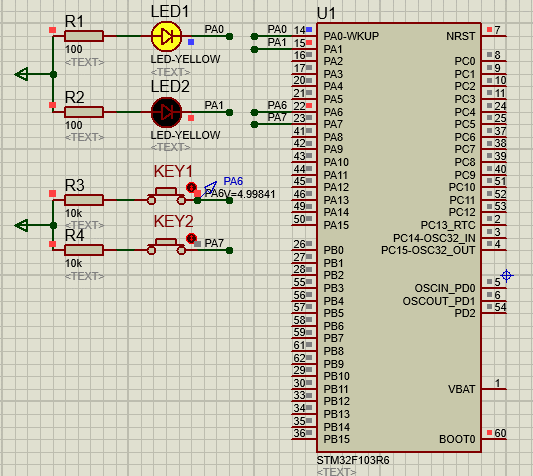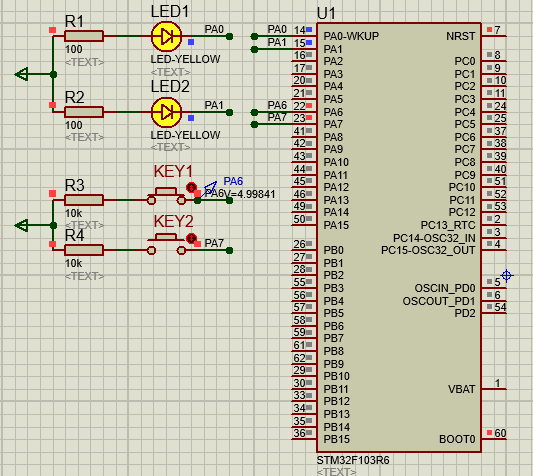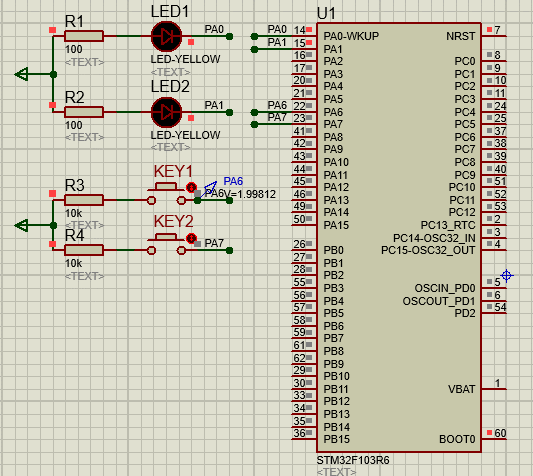
STM32-03基于HAL库(CubeMX+MDK+Proteus)输入检测案例(按键控制LED)
文章目录 一、功能需求分析二、Proteus绘制电路原理图三、STMCubeMX 配置引脚及模式,生成代码四、MDK打开生成项目,编写HAL库的按键检测代码五、运行仿真程序,调试代码 一、功能需求分析 搭建完成开发STM32开发环境之后,开始GPIO…...

DS3231SN
这份文件是关于DS3231SN芯片的数据手册,由Maxim Integrated公司生产。DS3231SN是一款高精度的I2C接口集成实时时钟(RTC)/温度补偿晶体振荡器(TCXO)/晶体的芯片。以下是该芯片的核心内容概述: 产品概述&…...

tsconfig.json文件翻译
原文件 {"compilerOptions": {/* Visit https://aka.ms/tsconfig to read more about this file *//* Projects */// "incremental": true, /* Save .tsbuildinfo files to allow for incremental compilation of projects.…...

树状数组学习笔记
树状数组 拜读了大佬的讲解博文(树状数组(详细分析应用),看不懂打死我!),写一篇Python版的笔记巩固消化,附带蓝桥杯历年真题作为例题演示 一、作用 用于快速读取列表中 某个区间内所有元素的和 实现单点修改ÿ…...

【bugfix】如何解决svg到线上显示空白或者svg的viewBox为空
svgo的默认机制是当width和height和viewbox一样会删除viewbox,这都是为了svg的压缩做的,详情可以看issue中的讨论,我们可以通过更改babel的配置来解决 https://github.com/svg/svgo/issues/1128 https://github.com/ant-design/ant-design-we…...
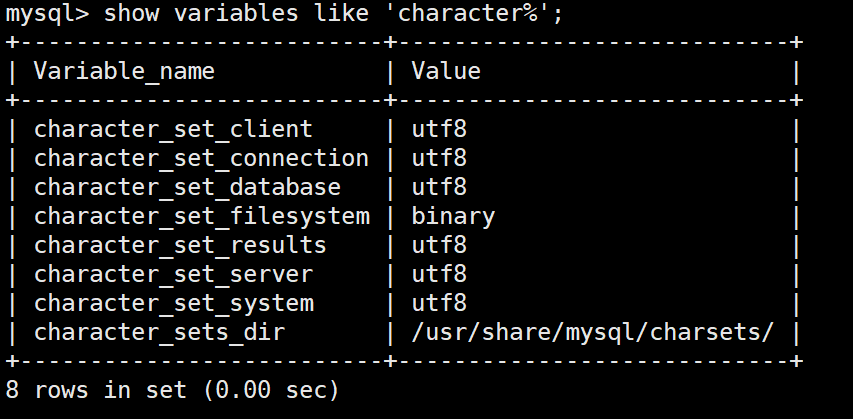
docker基础学习指令
文章目录 [toc] docker基础常用指令一、docker 基础命令二、docker 镜像命令1. docker images2. docker search3. docker pull4. docker system df5. docker rmi1. Commit 命令 三、 docker 容器命令1. docker run2. docker logs3. docker top4. docker inspect5. docker cp6. …...

回溯大学生活
回顾一下大学四年 bg:湖南大学 20级计科,成绩60%,无考研考公打算 四年之前,怀着激动的心情来到了大学校园,经过了太久的压抑终于迎来了高中老师口中的美好的大学生活,然而呢事实并非如此。恋爱呢…...

Android Fence机制
Android Fence机制 Android中的GraphicBuffer同步机制-Fence (最全最详细,推荐) AndroidQ 图形系统(5)Fence机制简介 Android P 图形显示系统(十一) BufferQueue(二)...
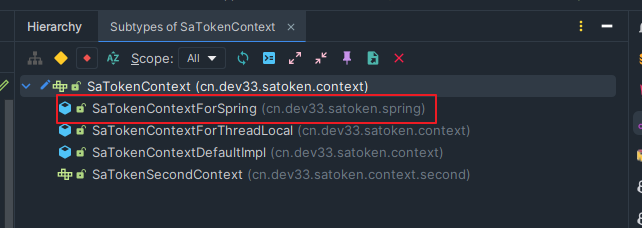
sa-token非Web上下文无法获取Request
0x02 非Web上下文无法获取Request 问题定位 在我们使用sa-token安全框架的时候,有时候会提示:**SaTokenException:非Web上下文无法获取Request**** 错误截图: 在官方网站中,查看常见问题排查: 非Web上下文无法获取…...

tomcat 常见优化方案
tomcat作为Web服务器,它的处理性能直接关系到用户体验,下面是几种常见的优化措施: 对web.xml的监视,把jsp提前编辑成Servlet。有富余物理内存的情况,加大tomcat使用的jvm的内存 服务器所能提供CPU、内存、硬盘的性能…...

前端导出文本内容为csv文件,excel乱码
原因:编码格式问题,需要改为utf-8 bom // Create blob with utf8-bom 编码 const createBlobWithBOM(data, mimeType)> {const bom [0xEF, 0xBB, 0xBF];const bomArray new Uint8Array(bom);const dataArray new TextEncoder().encode(data);const…...
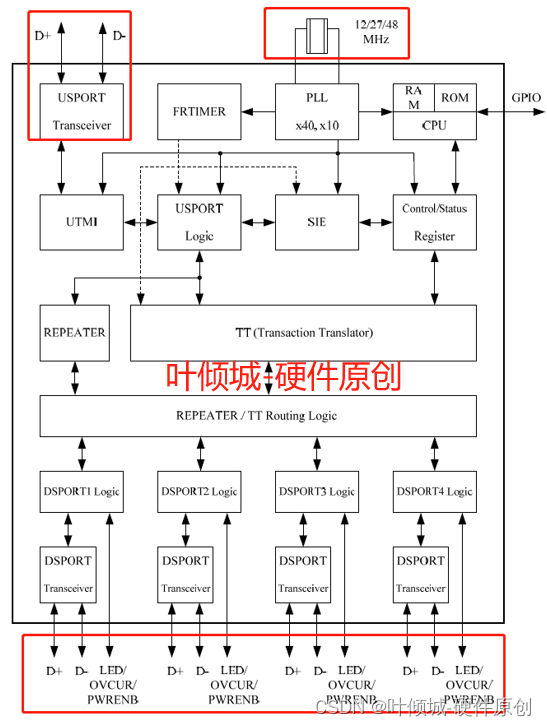
36---USB HUB电路设计
视频链接 USB HUB电路设计01_哔哩哔哩_bilibili USB HUB 电路设计 1、USB HUB基本介绍 USB Hub,指的是一种可以将一个USB接口扩展为多个,并可以使这些接口同时使用的装置。 Hub也是大家常说的集线器,它使用星型拓扑结构连接多个USB接口设…...

FPGA在深度学习领域的应用的优势
FPGA(Field-Programmable Gate Array)是一种可编程逻辑芯片,可以根据需要重新配置其内部的逻辑电路和功能。在深度学习领域,FPGA被广泛用于加速模型训练和推理任务。 首先,FPGA可以提供高度定制化的计算架构ÿ…...

Windows Edge 兼容性问题修复 基本解决方案
Windows Edge 浏览器兼容性问题可能源于多个方面,以下是一些常见的问题及其处理结果: 插件或扩展冲突:某些第三方插件或扩展可能与Edge浏览器不兼容,导致崩溃或运行异常。处理结果为,尝试禁用所有插件和扩展ÿ…...
【Servlet】服务器内部转发以及客户端重定向
文章目录 一、服务器内部转发:request.getRequestDispatcher("...").forward(request, response);二、客户端重定向:response.sendRedirect("");三、服务器内部转发代码示例四、客户端重定向代码示例 一、服务器内部转发:…...

是否有替代U盘,可安全交换的医院文件摆渡方案?
医院内部网络存储着大量的敏感医疗数据,包括患者的个人信息、病历记录、诊断结果等。网络隔离可以有效防止未经授权的访问和数据泄露,确保这些敏感信息的安全。随着法律法规的不断完善,如《网络安全法》、《个人信息保护法》等,医…...

观成科技:隐蔽隧道工具Ligolo-ng加密流量分析
1.工具介绍 Ligolo-ng是一款由go编写的高效隧道工具,该工具基于TUN接口实现其功能,利用反向TCP/TLS连接建立一条隐蔽的通信信道,支持使用Let’s Encrypt自动生成证书。Ligolo-ng的通信隐蔽性体现在其支持多种连接方式,适应复杂网…...

深入浅出Asp.Net Core MVC应用开发系列-AspNetCore中的日志记录
ASP.NET Core 是一个跨平台的开源框架,用于在 Windows、macOS 或 Linux 上生成基于云的新式 Web 应用。 ASP.NET Core 中的日志记录 .NET 通过 ILogger API 支持高性能结构化日志记录,以帮助监视应用程序行为和诊断问题。 可以通过配置不同的记录提供程…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

云原生玩法三问:构建自定义开发环境
云原生玩法三问:构建自定义开发环境 引言 临时运维一个古董项目,无文档,无环境,无交接人,俗称三无。 运行设备的环境老,本地环境版本高,ssh不过去。正好最近对 腾讯出品的云原生 cnb 感兴趣&…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...
