树状数组学习笔记
树状数组
拜读了大佬的讲解博文(树状数组(详细分析+应用),看不懂打死我!),写一篇Python版的笔记巩固消化,附带蓝桥杯历年真题作为例题演示
一、作用
用于快速读取列表中 某个区间内所有元素的和 实现单点修改,区间查询
若以差分数组作为a[]则可实现 区间修改,单点查询 操作,是一个常用技巧
二、时间复杂度
传统方式
- 访问某个元素: O ( 1 ) O(1) O(1)
- 获得某区间元素和: O ( n ) O(n) O(n)
树状数组
- 访问某个元素: O ( l o g n ) O(logn) O(logn)
- 获得某区间元素和: O ( l o g n ) O(logn) O(logn)
三、规则
通过创建一个列表t,记录以二进制划分的区间内元素的和,其中lowbit(x)的位数决定本节点所处的层数,t[x]保存了以x为根的子树中叶节点的值(即区间的元素和)
通过观察,
a数组具有以下性质:
- 下标索引从1开始(切记!!!)
- 长度为n
t数组具有以下性质: - t [ x ] t[x] t[x] 节点覆盖的长度是 l o w b i t ( x ) lowbit(x) lowbit(x)
- t [ x ] t[x] t[x] 的父节点是 t [ x + l o w b i t ( x ) ] t[x + lowbit(x)] t[x+lowbit(x)]
- 树的深度为 l o g 2 n + 1 log_2n + 1 log2n+1
- t [ x ] t[x] t[x] 节点覆盖的区间为 [ x − l o w b i t ( x ) + 1 , x ] [x-lowbit(x)+1, x] [x−lowbit(x)+1,x], t [ x ] t[x] t[x] 也即等于 t [ x ] t[x] t[x] 的子节点区间以后到$ a[x]$ 的所有元素之和!
t [ x ] ≡ ∑ i = x − l o w b i t ( x ) + 1 x a [ i ] t[x] \equiv \sum_{i = x-lowbit(x)+1}^x a[i] t[x]≡∑i=x−lowbit(x)+1xa[i]
四、创建和维护树状数组的三个基本函数
树状数组不是标准库中的数据结构,而是一个通过特殊函数维护和操作的一维数组。要想在题目中使用树状数组,首先需要创建三个操作函数。以下是这三个函数的详解。
(1)取最低二进制位函数 lowbit()
lowbit()函数用于获取一个正整数在二进制表示下最低位的1与其右侧所有的0所构成的二进制数的数值。
例如 12 = 2 ′ b 1100 , l o w b i t ( 12 ) = 2 ′ b 100 = 4 12 = 2'b1100, lowbit(12) = 2'b100 = 4 12=2′b1100,lowbit(12)=2′b100=4
# 正负x按位与
def lowbit(x):return (-x)&x
(2)单点修改函数 add()
为了实现树状数组的单点修改操作,需要创建一个函数add()。
由于每一个树上节点的祖先节点的值都包含了该节点的值,所以在修改某一个点的时候需要从叶子节点开始逐级向上递归修改它所有祖先节点的值。
这里就需要根据当前节点的序号 i i i 找出其双亲节点的序号,由树状数组的性质可知其双亲结点的序号为 i + l o w b i t ( i ) i+lowbit(i) i+lowbit(i)(见规则2)
def add(x,v):global n # n = len(t)while x < n:t[x] += vx += lowbit(x)
(3)区间查询函数 ckeck()
建立树状数组后,就可以利用其性质进行快速的区间查询了,由 规则4 可推知,区间[1,x]的元素和等于 t [ 1 ] + ⋅ ⋅ ⋅ + t [ x − l o w b i t ( x ) ] + t [ x ] t[1] + ··· + t[x-lowbit(x)] + t[x] t[1]+⋅⋅⋅+t[x−lowbit(x)]+t[x],由此可以使用递推求出区间和
# 求出区间[1:x+1]内所有元素的和
def check(x):ans = 0while x > 0:ans += t[x]x -= lowbit(x)return ans
以上函数无法指定区间的左端点,为了求出指定端点的区间和,可以使用类似于前缀和的方法求出指定区间的和值
# 求出区间[x:y]内所有元素的和
def check(left,right):ans = 0x = right - 1# 先使用原方法求出区间[1:right]的区间和while x > 0:ans += t[x]x -= lowbit(x)# 然后减去区间[1:left]的元素和,即可获得答案x = left-1while x > 0:ans -= t[x]x -= lowbit(x)return ans
五、树状数组整体模板
(1)单点修改、区间查询模板
def lowbit(x):return x&(-x)def add(x,v):global n,twhile x < n:t[x] += vx += lowbit(x)def check(left, right):global tx = right - 1ans = 0while x > 0:ans += t[x]x -= lowbit(x)x = left - 1while x > 0:ans -= t[x]x -= lowbit(x)return ans # 创建原数组和树状数组
# 注意树状数组的序号从1开始
a = [0] + [int(i) for i in input().split()]
n = len(a)
t = [0]*n
# 初始化树状数组
# 方法和初始化前缀和数组类似,将每一位的元素加到t[]中
for i in range(1,n):add(i,a[i])
# 查询修改前的区间和
print(check(2,6))
# 修改原数组中某一元素的值(单点修改)
index,value = map(int,input().split())
add(index, value)
# 查询修改后的区间和(区间查询)
print(check(2,6))
# 具体功能(略),按照题目要求编写
(2)区间修改、单点查询模板
def lowbit(x):return x&(-x)
def add(x,v):global x,twhile x < n:t[x] += v
def check(left,right):global n,tx = right - 1while x > 0:ans += t[x]x -= lowbit(x)x = left - 1while x > 0:ans -= t[x]x -= lowbit(x)return
# 初始化原数组和树状数组
a = [0] + [int(i) for i in input().split()]
n = len(a)
t = [0]*(n+1)
d = [0]*(n+1)
# 用树状数组维护差分数组
for i in range(1,n):d[i] = a[i] - a[i-1]add(i,d[i])
# 区间修改
l,r,v = map(int,input().split())
# 结合差分数组修改的原理在树状数组上进行单点修改
# 修改d[l],d[r+1]
add(l,v)
add(r+1,-v)
# 单点查询
# 查询原数组第三个元素的值
print(check(3))
六、例题
例题一:异或和(蓝桥杯第14届省赛)
问题描述:
给一棵含有 n n n 个结点的有根树,根结点为 1 1 1 ,编号为 i i i 的点有点权 a i a_i ai ( i ∈ [ 1 , n ] ) (i \in [1,n]) (i∈[1,n])。现在有两种操作,格式如下:
1 x y 1 x y 1xy :该操作表示将点 x x x 的点权改为 y y y。
2 x 2 x 2x :该操作表示查询以结点 x x x 为根的子树内的所有点的点权的异或和。
现有长度为 m m m 的操作序列,请对于每个第二类操作给出正确的结果。
输入格式:
输入的第一行包含两个正整数 n , m n,m n,m 用一个空格分隔。第二行包含 n n n 个整数 $a_1, a_2, … ,a_n
,相邻整数之间使用一个空格分隔。接下来 n − 1 n−1 n−1 行,每行包含两个正整数 u i , v i u_i, v_i ui,vi,表示结点 u i u_i ui 和 v i v_i vi之间有一条边。接下来 m m m 行,每行包含一个操作。
输出格式:
输出若干行,每行对应一个查询操作的答案。
# 求 DFS 序,以便建立树状数组
cnt = 0
def dfs(cur,pre):# cur 是当前节点的序号,pre是上一个节点的序号global cntcnt += 1# 记录将当前节点压入栈中的时间戳seq[cur][0] = cnt for i in tree[cur]:if pre != i:dfs(i,cur)# 记录将当前元素出栈的时间戳,自此以后的时间戳均与以cur为根节点的树无关seq[cur][1] = cnt # 树状数组函数三件套
def lowbit(x):return x&(-x)def modify(x,v):global nwhile x <= n:t[x] ^= v # 计算异或和x += lowbit(x)def query(x):global nans = 0while x > 0:ans ^= t[x]x -= lowbit(x)return ans# 接收输入,创建数据结构
n,m = map(int,input().split())
# a[]存储每一个点的权值
a = [0] + [int(i) for i in input().split()]# 用邻接表存储树结构
tree = [[] for i in range(n+1)]
for _ in range(n-1):u,v = map(int,input().split())# 注意没说方向,是一个无向边tree[u].append(v)tree[v].append(u)# 创建一个二维数组seq[][]记录DFS序
# 其中seq[i]是有2个元素的列表,两个元素分别是第i个节点入栈和出栈的时间戳
seq = [[0,0] for i in range(n+1)]
dfs(1,0)# 为DFS序数组创建树状数组,并用a[]的值初始化
t = [0]*(n+1)
for i in range(1,n+1):modify(seq[i][0], a[i])
for _ in range(m):instr = [int(i) for i in input().split()]if instr[0] == 1:# 修改元素,注意到需要在赋值的同时清除原有元素,所以将原值与新值异或,相当于清除原值modify(seq[instr[1]][0], a[instr[1]]^instr[2])# 维护a[],确保其始终保存着每一个节点的当前值a[instr[1]] = instr[2]else:# 输出单点查询结果 print(query(seq[instr[1]][1]) ^ query(seq[instr[1]][0] - 1))
相关文章:

树状数组学习笔记
树状数组 拜读了大佬的讲解博文(树状数组(详细分析应用),看不懂打死我!),写一篇Python版的笔记巩固消化,附带蓝桥杯历年真题作为例题演示 一、作用 用于快速读取列表中 某个区间内所有元素的和 实现单点修改ÿ…...

【bugfix】如何解决svg到线上显示空白或者svg的viewBox为空
svgo的默认机制是当width和height和viewbox一样会删除viewbox,这都是为了svg的压缩做的,详情可以看issue中的讨论,我们可以通过更改babel的配置来解决 https://github.com/svg/svgo/issues/1128 https://github.com/ant-design/ant-design-we…...
docker基础学习指令
文章目录 [toc] docker基础常用指令一、docker 基础命令二、docker 镜像命令1. docker images2. docker search3. docker pull4. docker system df5. docker rmi1. Commit 命令 三、 docker 容器命令1. docker run2. docker logs3. docker top4. docker inspect5. docker cp6. …...

回溯大学生活
回顾一下大学四年 bg:湖南大学 20级计科,成绩60%,无考研考公打算 四年之前,怀着激动的心情来到了大学校园,经过了太久的压抑终于迎来了高中老师口中的美好的大学生活,然而呢事实并非如此。恋爱呢…...

Android Fence机制
Android Fence机制 Android中的GraphicBuffer同步机制-Fence (最全最详细,推荐) AndroidQ 图形系统(5)Fence机制简介 Android P 图形显示系统(十一) BufferQueue(二)...
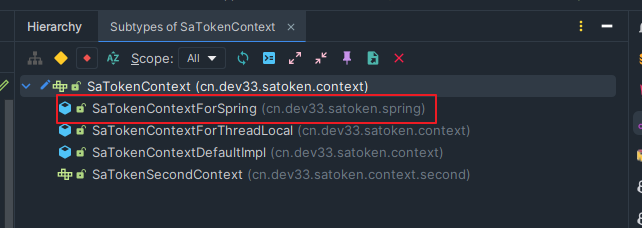
sa-token非Web上下文无法获取Request
0x02 非Web上下文无法获取Request 问题定位 在我们使用sa-token安全框架的时候,有时候会提示:**SaTokenException:非Web上下文无法获取Request**** 错误截图: 在官方网站中,查看常见问题排查: 非Web上下文无法获取…...

tomcat 常见优化方案
tomcat作为Web服务器,它的处理性能直接关系到用户体验,下面是几种常见的优化措施: 对web.xml的监视,把jsp提前编辑成Servlet。有富余物理内存的情况,加大tomcat使用的jvm的内存 服务器所能提供CPU、内存、硬盘的性能…...

前端导出文本内容为csv文件,excel乱码
原因:编码格式问题,需要改为utf-8 bom // Create blob with utf8-bom 编码 const createBlobWithBOM(data, mimeType)> {const bom [0xEF, 0xBB, 0xBF];const bomArray new Uint8Array(bom);const dataArray new TextEncoder().encode(data);const…...
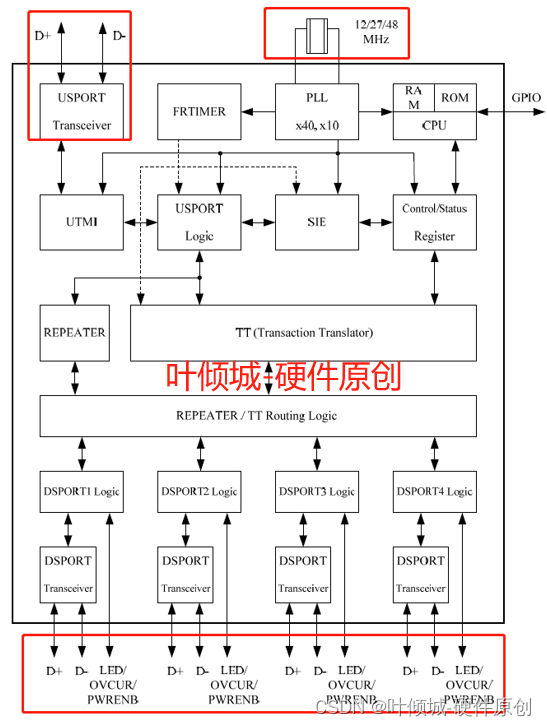
36---USB HUB电路设计
视频链接 USB HUB电路设计01_哔哩哔哩_bilibili USB HUB 电路设计 1、USB HUB基本介绍 USB Hub,指的是一种可以将一个USB接口扩展为多个,并可以使这些接口同时使用的装置。 Hub也是大家常说的集线器,它使用星型拓扑结构连接多个USB接口设…...

FPGA在深度学习领域的应用的优势
FPGA(Field-Programmable Gate Array)是一种可编程逻辑芯片,可以根据需要重新配置其内部的逻辑电路和功能。在深度学习领域,FPGA被广泛用于加速模型训练和推理任务。 首先,FPGA可以提供高度定制化的计算架构ÿ…...

Windows Edge 兼容性问题修复 基本解决方案
Windows Edge 浏览器兼容性问题可能源于多个方面,以下是一些常见的问题及其处理结果: 插件或扩展冲突:某些第三方插件或扩展可能与Edge浏览器不兼容,导致崩溃或运行异常。处理结果为,尝试禁用所有插件和扩展ÿ…...
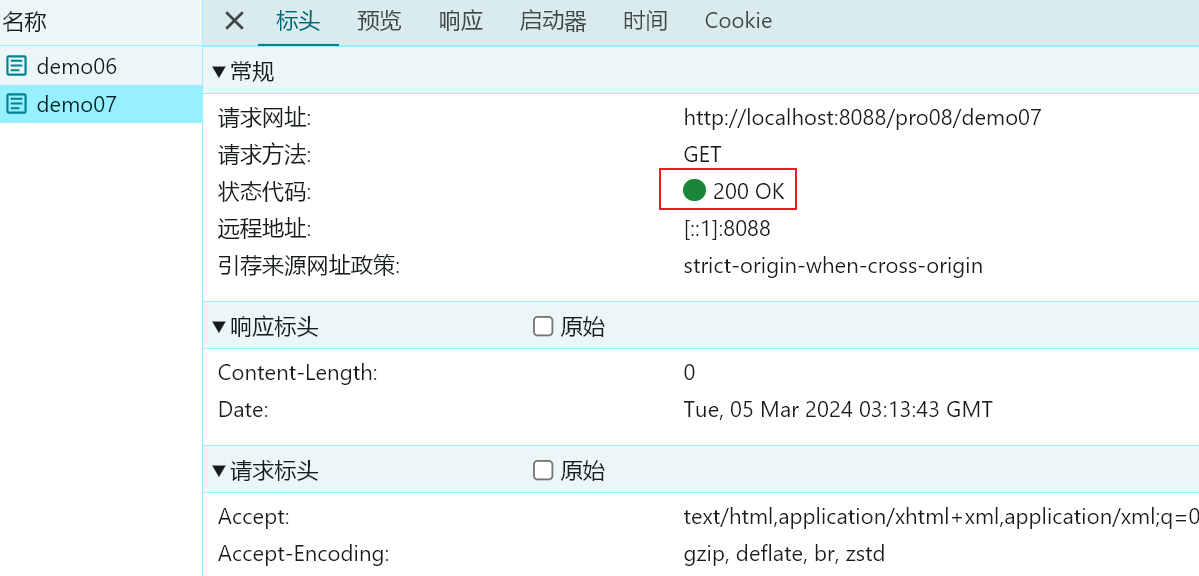
【Servlet】服务器内部转发以及客户端重定向
文章目录 一、服务器内部转发:request.getRequestDispatcher("...").forward(request, response);二、客户端重定向:response.sendRedirect("");三、服务器内部转发代码示例四、客户端重定向代码示例 一、服务器内部转发:…...

是否有替代U盘,可安全交换的医院文件摆渡方案?
医院内部网络存储着大量的敏感医疗数据,包括患者的个人信息、病历记录、诊断结果等。网络隔离可以有效防止未经授权的访问和数据泄露,确保这些敏感信息的安全。随着法律法规的不断完善,如《网络安全法》、《个人信息保护法》等,医…...

Java设计模式详解:单例模式
设计模式详解:单例模式 文章目录 设计模式详解:单例模式一、单例模式的原理二、单例模式的实现推荐1、饿汉模式2、静态内部类 三、单例模式的案例四、单例模式的使用场景推荐总结 一、单例模式的原理 单例模式听起来很高大上,但其实它的核心…...

Pointnet++改进即插即用系列:全网首发OREPA在线重新参数化卷积,替代普通卷积 |即插即用,提升特征提取模块性能
简介:1.该教程提供大量的首发改进的方式,降低上手难度,多种结构改进,助力寻找创新点!2.本篇文章对Pointnet++特征提取模块进行改进,加入OREPA,提升性能。3.专栏持续更新,紧随最新的研究内容。 目录 1.理论介绍 2.修改步骤 2.1 步骤一 2.2 步骤二 2.3 步骤三...
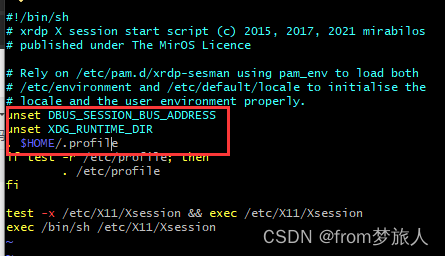
XRDP登录ubuntu桌面闪退问题
修改 /etc/xrdp/startwm.sh unset DBUS_SESSION_BUS_ADDRESS unset XDG_RUNTIME_DIR . $HOME/.profile...

【Node】使用Node.js构建简单的静态页面生成器
使用Node.js构建简单的静态页面生成器 在现代的Web开发中,静态网站因其速度快、安全性高而越来越受到开发者的青睐。本文将介绍如何使用Node.js构建一个简单的静态页面生成器,通过这个小项目,你将了解到静态网站生成的基本原理和实现方法。 …...

AI智能客服机器人是什么?对企业重要吗?
在数字化时代,客户服务是企业与客户建立牢不可破关系的重要桥梁。AI智能客服机器人,顾名思义,就是利用人工智能技术提升客户服务体验的自动化工具。今天,就让我们来揭开AI智能客服机器人的神秘面纱,并讨论它对企业的重…...

InfluxDB2的数据查询示例
有用influxdb2 不支持sql,并且实质是个列存储数据库,这里基于 influxdb-client-java 和 beanutils反射,写了个数据查询,把结果以行对象的形式返回的工具类。 package com.joy.malltools.influxdb2;import com.influxdb.client.Q…...

CSS基础语法-黑马跟课笔记-供记录与查询
一.CSS简介 1.1HTML局限性 只关注内容的语义,可以做简单的样式但是很臃肿且繁琐 1.2CSS优势 CSS层叠样式表,标记语言 设置HTML页面中的文本内容,图片外形,可以美化HTML,让页面布局更美观 HTML做框架,…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Caliper 配置文件解析:config.yaml
Caliper 是一个区块链性能基准测试工具,用于评估不同区块链平台的性能。下面我将详细解释你提供的 fisco-bcos.json 文件结构,并说明它与 config.yaml 文件的关系。 fisco-bcos.json 文件解析 这个文件是针对 FISCO-BCOS 区块链网络的 Caliper 配置文件,主要包含以下几个部…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

Qemu arm操作系统开发环境
使用qemu虚拟arm硬件比较合适。 步骤如下: 安装qemu apt install qemu-system安装aarch64-none-elf-gcc 需要手动下载,下载地址:https://developer.arm.com/-/media/Files/downloads/gnu/13.2.rel1/binrel/arm-gnu-toolchain-13.2.rel1-x…...

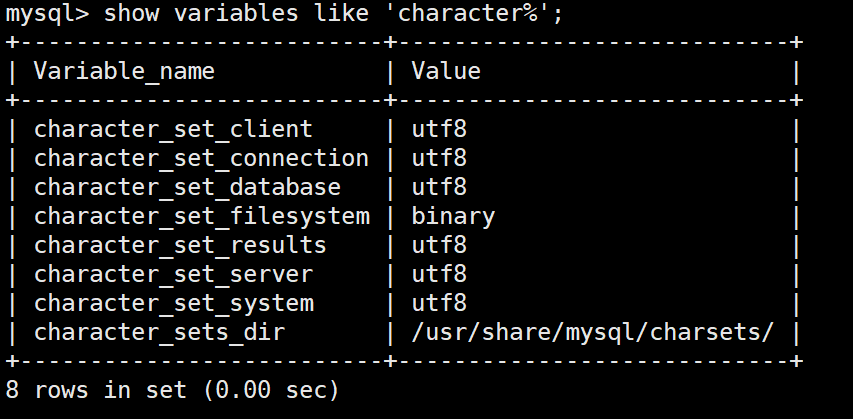
MySQL:分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区(Partitioning)是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分(分区)可以独立存储、管理和优化,…...

从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析,分为已启动和未启动两种场景: 一、ContentProvider已启动的情况 1. 核心流程 触发条件:当其他组件(如Activity、Service)通过ContentR…...

Spring Security 认证流程——补充
一、认证流程概述 Spring Security 的认证流程基于 过滤器链(Filter Chain),核心组件包括 UsernamePasswordAuthenticationFilter、AuthenticationManager、UserDetailsService 等。整个流程可分为以下步骤: 用户提交登录请求拦…...
