[蓝桥杯练习]通电


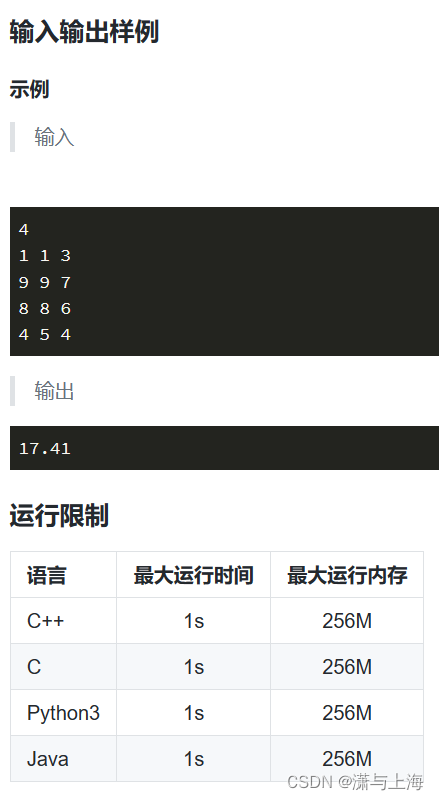
kruskal做法(加边)
#include <bits/stdc++.h>
using namespace std;
int x[10005],y[10005],z[10005];//存储i点的x与y坐标
int bcj[10005];//并查集
struct Edge{//边 int v1,v2; double w;
}edge[2000005];
int cmp(Edge a, Edge b){return a.w < b.w;}
int find(int x){//并查集查找 if(bcj[x]!=x)bcj[x]=find(bcj[x]);//带路径压缩return bcj[x];
}
void merge(int v1,int v2){//并查集合并 v1=find(v1);v2=find(v2);bcj[v2]=v1;
}
int main(){//int n;cin>>n;for(int i=1;i<=n;++i)bcj[i]=i;//并查集初始化//for(int i=1;i<=n;i++)cin>>x[i]>>y[i]>>z[i];//读取结点x坐标y坐标 int cnt=0;for(int v1=1;v1<=n;++v1)for(int v2=v1+1;v2<=n;++v2){//求出任意两点的权重 double w=sqrt(pow((x[v1]-x[v2]),2)+pow((y[v1]-y[v2]),2))+pow((z[v1]-z[v2]),2);//v1的x坐标减去v2的x坐标... edge[++cnt]={v1,v2,w};}sort(edge+1,edge+cnt+1,cmp);int MSTm = 0;double sumw = 0.0;//解决了任意孤立点(一个点就是一个集合),然后对每个点作n-1个点的相连边并排序,保证每次取得是最短的,并且使用并查集避免出现环路. //取得边是离散的,总可以取完 for(int i=1;i<=cnt;++i){//依次取得边,其权重递增 if(find(edge[i].v1)!=find(edge[i].v2)){//若两边端点不属于同一个集合,则合并 merge(edge[i].v1,edge[i].v2);//每次取一条边并将其标记为一个集合,使其不出现环路 ++MSTm;sumprimzuofaw+=edge[i].w;//获取MST中最大的边 }if(MSTm==n-1)break;//n-1条边就可以构造MST }cout<<fixed<<setprecision(2)<<sumw<<endl;return 0;
}
prim做法(加点)
#include <bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int MAXN = 1005;
vector<int> demo;
double closest[MAXN], lowcost[MAXN];
int m, n; // m为节点的个数,n为边的数量
double G[MAXN][MAXN]; // 邻接矩阵
double prim()
{for (int i = 0; i < m; i++){lowcost[i] = INF;}for (int i = 0; i < m; i++){closest[i] = 0;}closest[0] = -1; // 加入第一个点,-1表示该点在集合U中,否则在集合V中int num = 0, e = 0; // e为最新加入集合的点double ans=0;while (num < m - 1) // 加入m-1条边{int miedge = -1;double micost = INF;for (int i = 0; i < m; i++)if (closest[i] != -1){double temp = G[e][i];if (temp < lowcost[i]){lowcost[i] = temp;closest[i] = e;}if (lowcost[i] < micost)micost = lowcost[miedge = i];}ans += micost;demo.push_back(micost);closest[e = miedge] = -1;num++;}return ans;
}struct node
{double x, y, h;
} dis[MAXN];double getDistance(node a, node b)
{return sqrt(pow(a.x - b.x, 2) + pow(a.y - b.y, 2)) + pow(a.h - b.h, 2);
}int main()
{scanf("%d", &m);for (int i = 0; i < m; i++)scanf("%lf%lf%lf", &dis[i].x, &dis[i].y, &dis[i].h);for (int i = 0; i < m - 1; i++)for (int j = i + 1; j < m; j++){G[i][j] = getDistance(dis[i], dis[j]);G[j][i] = G[i][j];}printf("%.2lf", prim());// for (int i = 0; i < m - 1; i++)// cout << demo[i] << " ";return 0;
}
相关文章:

[蓝桥杯练习]通电
kruskal做法(加边) #include <bits/stdc.h> using namespace std; int x[10005],y[10005],z[10005];//存储i点的x与y坐标 int bcj[10005];//并查集 struct Edge{//边 int v1,v2; double w; }edge[2000005]; int cmp(Edge a, Edge b){return a.w < b.w;} int find(i…...

安全算法 - 摘要算法
摘要算法是一种将任意长度的数据转换为固定长度字节串的算法。它具有以下特点和应用。 首先,摘要算法能够生成一个唯一且固定长度的摘要值,用于验证数据的完整性和一致性。无论输入数据有多长,生成的摘要值始终是固定长度的,且即…...

操作系统:动静态库
目录 1.动静态库 1.1.如何制作一个库 1.2.静态库的使用和管理 1.3.安装和使用库 1.4.动态库 1.4.1.动态库的实现 1.4.2.动态库与静态库的区别 1.4.3.共享动态库给系统的方法 2.动态链接 2.1.操作系统层面的动态链接 1.动静态库 静态库(.a)&…...

车载电子电器架构 —— 局部网络管理汇总
车载电子电器架构 —— 局部网络管理汇总 我是穿拖鞋的汉子,魔都中坚持长期主义的汽车电子工程师。 老规矩,分享一段喜欢的文字,避免自己成为高知识低文化的工程师: 屏蔽力是信息过载时代一个人的特殊竞争力,任何消耗你的人和事,多看一眼都是你的不对。非必要不费力证明…...

网络安全 | 什么是DDoS攻击?
关注WX:CodingTechWork DDoS-介绍 DoS:Denial of Service,拒绝服务。DDoS是通过大规模的网络流量使得正常流量不能访问受害者目标,是一种压垮性的网络攻击,而不是一种入侵手段。NTP网络时间协议,设备需要…...

[Godot] 3D拾取
CollisionObject3D文档 Camera3D文档 CollisionObject3D有个信号_input_event,可以用于处理3D拾取。 Camera3D也有project_position用于将屏幕空间坐标投影到3D空间。 extends Node3D#是否处于选中状态 var selected : bool false #摄像机的前向量 var front : V…...
知识融合:知识图谱构建的关键技术
目录 一、引言二、知识图谱基础2.1 知识表示三元组属性图 2.2 知识抽取实体抽取关系抽取属性抽取 三、知识融合的核心问题3.1 实体识别与链接实体识别实体链接 3.2 重复实体合并方法示例 3.3 关系融合挑战方法示例 四、知识融合技术深度解析4.1 基于规则的方法规则设计原则规则…...
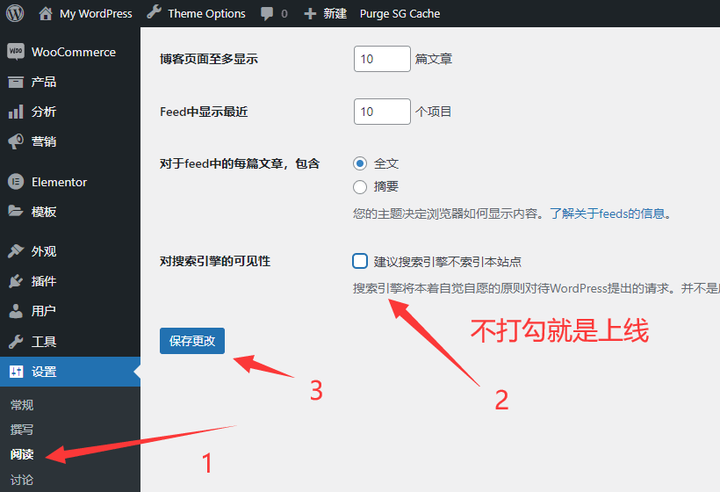
外贸建站:WordPress搭建外贸独立站零基础自建站完整教程(2024)
对于做外贸来说,拥有自己的外贸独立网站真的非常重要。在外贸领域,如今各平台竞争激烈,规则多,成本高,价格战、政策变化快,还存在封店风险等等因素。在这种情况下,拥有外贸独立站就能很好规避上…...

【教程】Kotlin语言学习笔记(五)——Lambda表达式与条件控制
写在前面: 如果文章对你有帮助,记得点赞关注加收藏一波,利于以后需要的时候复习,多谢支持! 【Kotlin语言学习】系列文章 第一章 《认识Kotlin》 第二章 《数据类型》 第三章 《数据容器》 第四章 《方法》 第五章 《L…...

C++的并发世界(三)——线程对象生命周期
0.案例代码 先看下面一个例子: #include <iostream> #include <thread>void ThreadMain() {std::cout << "begin sub thread:" << std::this_thread::get_id()<<std::endl;for (int i 0; i < 10; i){std::cout <&…...
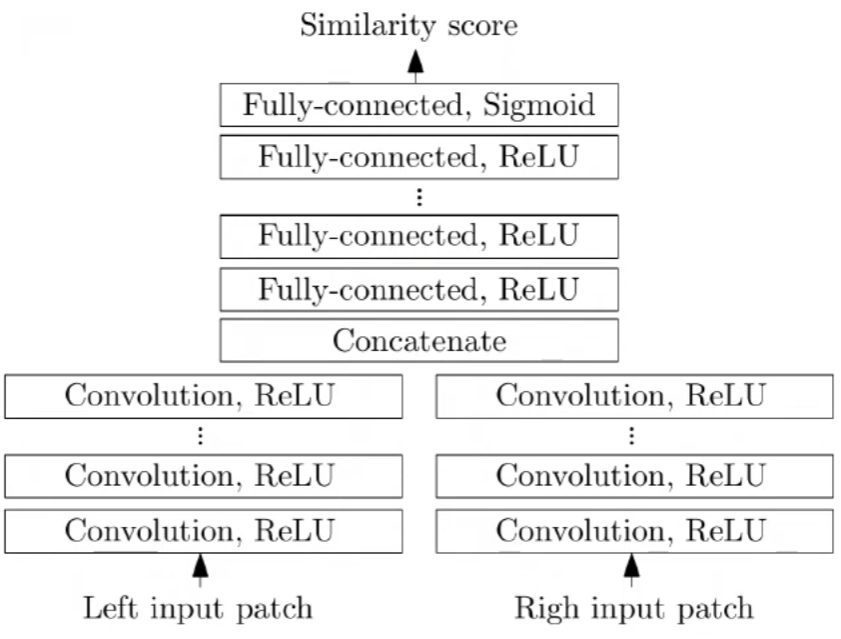
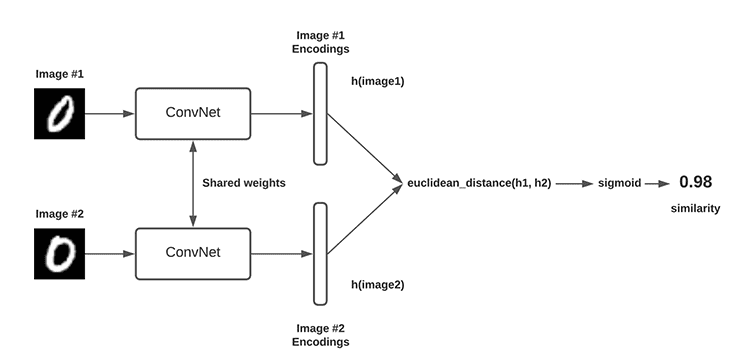
SAD法(附python实现)和Siamese神经网络计算图像的视差图
1 视差图 视差图:以左视图视差图为例,在像素位置p的视差值等于该像素在右图上的匹配点的列坐标减去其在左图上的列坐标 视差图和深度图: z f b d z \frac{fb}{d} zdfb 其中 d d d 是视差, f f f 是焦距, b b…...
基于DWT(离散小波变换)的图像加密水印算法,Matlab实现
博主简介: 专注、专一于Matlab图像处理学习、交流,matlab图像代码代做/项目合作可以联系(QQ:3249726188) 个人主页:Matlab_ImagePro-CSDN博客 原则:代码均由本人编写完成,非中介,提供…...
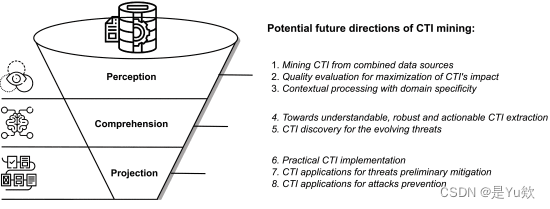
【威胁情报综述阅读3】Cyber Threat Intelligence Mining for Proactive Cybersecurity Defense
【威胁情报综述阅读1】Cyber Threat Intelligence Mining for Proactive Cybersecurity Defense: A Survey and New Perspectives 写在最前面一、介绍二、网络威胁情报挖掘方法和分类A. 研究方法1) 第 1 步 - 网络场景分析:2) 第 2 步 - 数据…...
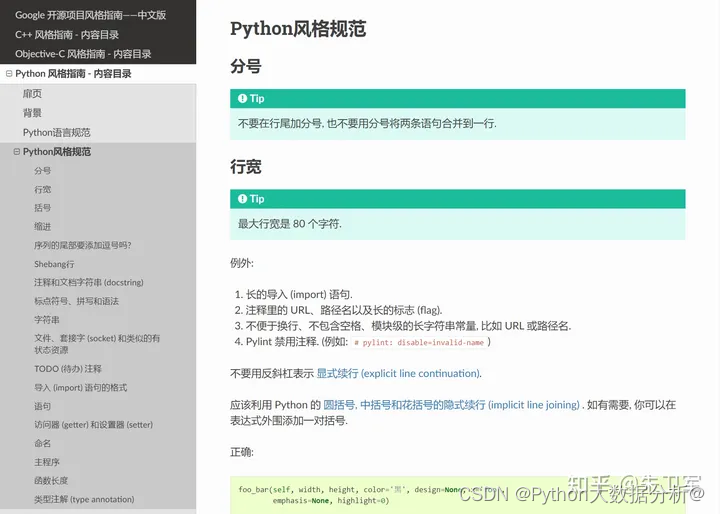
在编程中使用中文到底该不该??
看到知乎上有个热门问题,为什么很多人反对中文在编程中的使用? 这个问题有几百万的浏览热度,其中排名第一的回答非常简洁,我深以为然: 在国内做开发,用中文写注释、写文档,是非常好的习惯&…...

PyQt6从入门到放弃
PyQt6从入门到放弃 安装PyQt6 pip install PyQt6# 查看QT和PyQT的版本 from PyQt6.QtCore import QT_VERSION_STR from PyQt6.QtCore import PYQT_VERSION_STR print(QT_VERSION_STR) print(PYQT_VERSION_STR)PyQt6模块 PyQt6类由一系列模块组成包括QtCore、QtGui、QtWidgets…...

PhpWord导入试卷
规定word导入格式 1、[单选题][2024][一般]题目1 A.选项1 B.选项2 C.选项3 D.选项4 答案:D 试题图片(上传多媒体图片): 分数:2 答案解析: 2、[多选题][2024][困难]题目2 A.选项1 B.选项2 C.选项3 D.选项4 E…...

C# 运算符重载 之前的小总结
C# 中支持运算符重载,所谓运算符重载就是我们可以使用自定义类型来重新定义 C# 中大多数运算符的功能。运算符重载需要通过 operator 关键字后跟运算符的形式来定义的,我们可以将被重新定义的运算符看作是具有特殊名称的函数,与其他函数一样&…...
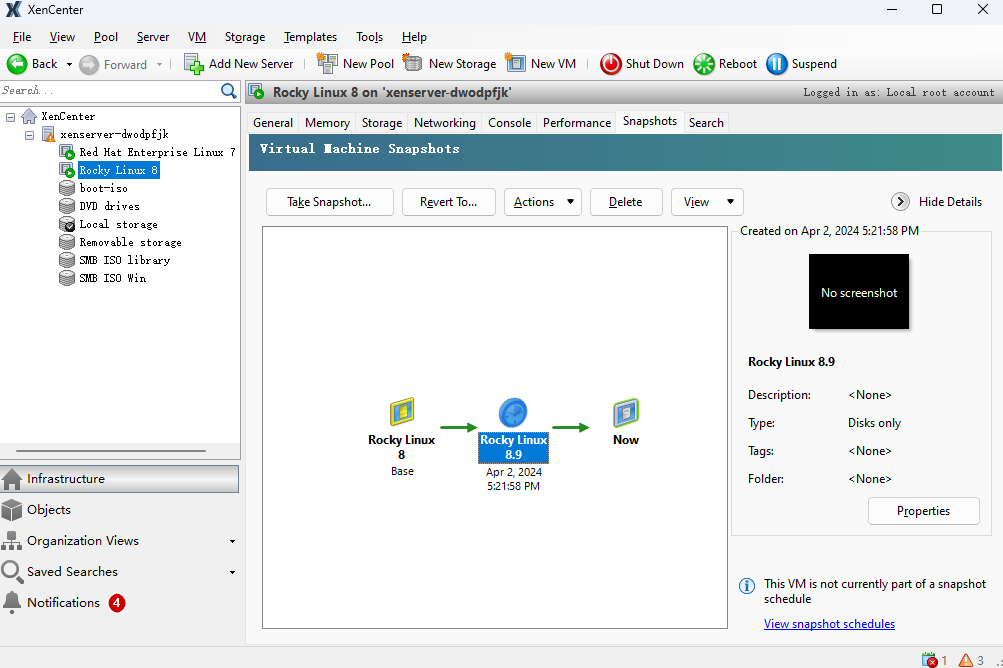
XenCenter 2024 创建一个虚拟机
前言 实现,创建一个虚拟机,内存,cpu,磁盘,名称,网卡,配置 Xen Center 2024 download 创建虚拟机 选择系统类型 定义虚拟机名称 选择ISO镜像库 选择主服务器 分配虚拟机内存,cpu资源…...

tomcat 知多少
Tomcat的缺省端口: 默认端口为8080,可以通过在tomcat安装包conf目录下,service.xml中的Connector元素的port属性来修改端口。 tomcat 常见 Connector 运行模式(优化): 这三种模式的不同之处如下: BIO : 一…...

【详细讲解语言模型的原理、实战与评估】
🌈个人主页:程序员不想敲代码啊🌈 🏆CSDN优质创作者,CSDN实力新星,CSDN博客专家🏆 👍点赞⭐评论⭐收藏 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

《信号与系统》第 6 章 信号与系统的时域和频域特性
目录 6.0 引言 6.1 傅里叶变换的模和相位表示 6.2 线性时不变系统频率响应的模和相位表示 6.2.1 线性与非线性相位 6.2.2 群时延 6.2.3 对数模和相位图 6.3 理想频率选择性滤波器的时域特性 6.4 非理想滤波器的时域和频域特性讨论 6.5 一阶与二阶连续时间系统 6.5.1 …...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

在Zenodo下载文件 用到googlecolab googledrive
方法:Figshare/Zenodo上的数据/文件下载不下来?尝试利用Google Colab :https://zhuanlan.zhihu.com/p/1898503078782674027 参考: 通过Colab&谷歌云下载Figshare数据,超级实用!!࿰…...
