稀疏矩阵的三元组表表示法及其转置
1. 什么是稀疏矩阵
稀疏矩阵是指矩阵中大多数元素为零的矩阵。
从直观上讲,当元素个数低于总元素的30%时,这样的矩阵被称为稀疏矩阵。
由于该种矩阵的特点,我们在存储这种矩阵时,如果直接采用二维数组,就会十分浪费空间,因为其中大多数元素都是重复的零。
稀疏矩阵的三元组表表示法
对于稀疏矩阵的压缩存储,采用只存储非零元素的方法。
由于稀疏矩阵中非零元素的分布没有规律,因此在存储非零元素值得同时,还必须存储该非零元素在矩阵中的位置信息,即行号和列号。
也就是采用三元组的结构存储:

为处理方便,将稀疏矩阵中非零元素对应的三元组行号依次增大进行存放。
这也就解释了,为什么稀疏矩阵是非零元素占比小于30%的矩阵。
因为采取三元组的结构储存,一个元素会占用三个单元的空间,只有当零元素占比小于30%时,这种存储结构才能在空间上有较明显的收益。
稀疏矩阵三元组表的类型定义
#define ElementType int//一个三元组元素
typedef struct
{int row, col;//非零元素行下标和列下标ElementType e;
}Triple;//稀疏矩阵
typedef struct
{Triple* data;//非零元素的三元组表int m, n, len;//矩阵行数,列数,非零元素个数int capacity;//容量
}TSMatrix;2. 对稀疏矩阵进行基本操作
//初始化稀疏矩阵
void TSMInite(TSMatrix* ps)
{assert(ps);ps->data = NULL;ps->m = TSM_ROWMAX;ps->n = TSM_COLMAX;ps->len = 0;ps->capacity = 0;
}//销毁稀疏矩阵
void TSMDestroy(TSMatrix* ps)
{assert(ps);free(ps->data);ps->data = NULL;ps->len = 0;ps->capacity = 0;
}//检查扩容
void CheckCapacity(TSMatrix* ps)
{assert(ps);if(ps->capacity == ps->len){int newcapacity = ps->capacity == 0 ? 4 : ps->capacity * 2;Triple* tmp = (Triple*)realloc(ps->data, newcapacity * sizeof(Triple));if(tmp == NULL){perror("realloc");exit(-1);}ps->data = tmp;ps->capacity = newcapacity;}
}//插入元素
void ElemInsert(TSMatrix* ps, Triple x)
{assert(ps);CheckCapacity(ps);if(ps->len == 0){ps->data[ps->len] = x;}if(x.row < ps->data[0].row){for(int j = ps->len; j > 0; j--){ps->data[j] = ps->data[j - 1];}ps->data[0] = x;}elsefor(int i = 0; i < ps->len; i++){if(x.row >= ps->data[i].row&&x.row <= ps->data[i + 1].row||i == ps->len - 1){for(int j = ps->len; j > i + 1; j--){ps->data[j] = ps->data[j - 1];}ps->data[i + 1] = x;break;}}ps->len++;
}//打印元素
void TSMPrint(TSMatrix ps)
{for(int i = 0; i < ps.len; i++){printf("row = %d col = %d e = %d\n", ps.data[i].row, ps.data[i].col, ps.data[i].e);}printf("\n");
}这些函数基本是以顺序表操作函数为蓝本写的,目的是为了方便我们实现稀疏矩阵的转置。
只不过插入元素的函数需要确保插入之后,三元组的行号是依次递增的。
3. 稀疏矩阵的转置
需要强调的是,矩阵的常规存储是二维的,而三元组表存储是一维的,由于矩阵存储结构的变化,也带来了运算方法的不同,必须认真分析。
3.1 稀疏矩阵转置的经典算法
void TransMatrix(ElementType source[m][n], ElementType dest[n][m])
{int i, j;for(i = 0; i < m; i++)for(j = 0; j < n; j++)dest[j][i] = source[i][j];
}这个算法是针对传统的二维数组的存储方式。
3.2 用三元组表实现稀疏矩阵的转置
假设A和B是稀疏矩阵source和dest的三元组表,则实现转置的简单方法如下:
1. 三元组表A的行,列互换就可以得到B中的元素。
2. 转置后的矩阵的三元组表B中的三元组不是以“行序为主序”存储的,为保证三元组表B也是以“行序为主序”进行存放的,则需要对该三元组表B按行下标(即A的列下标)以递增顺序重新排列。
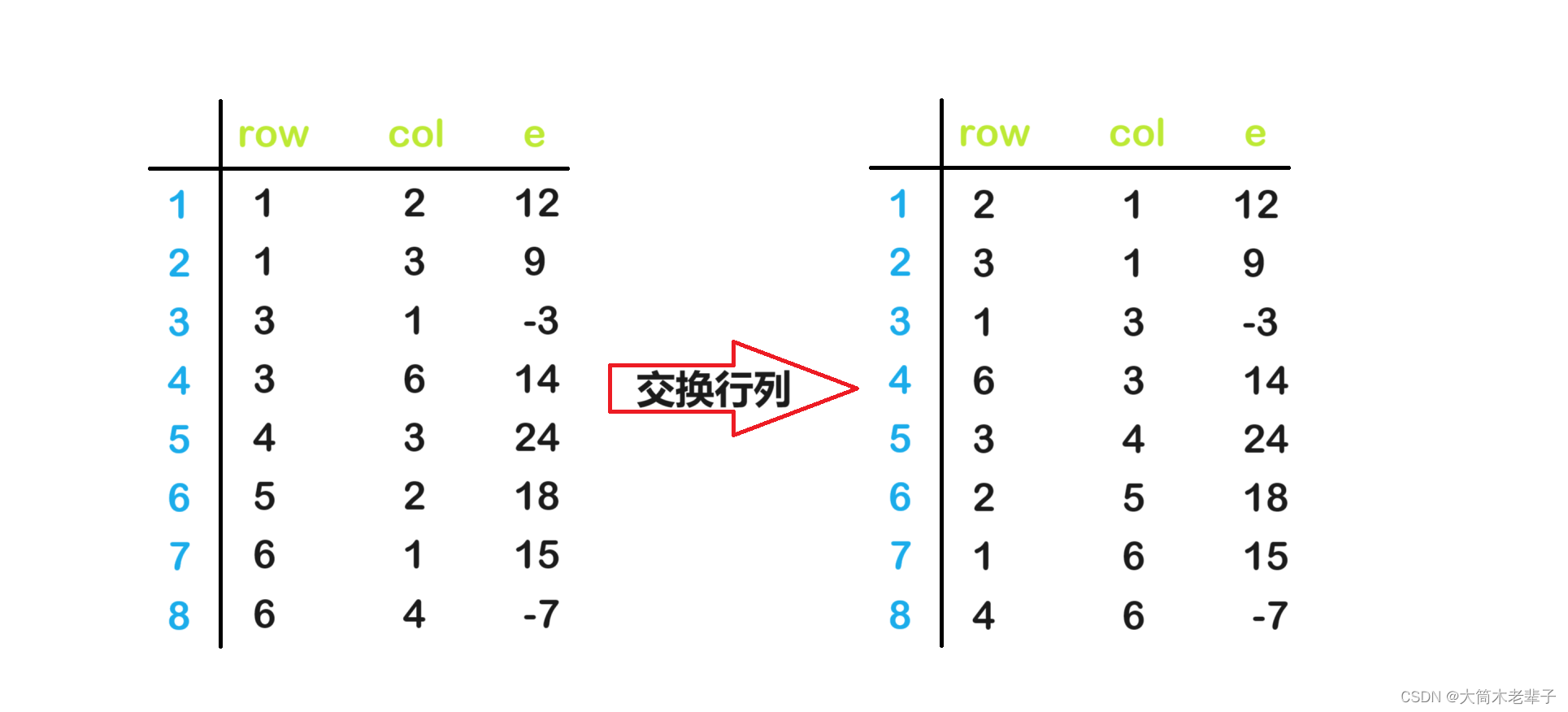
上图中的步骤很容易实现,但是重新排序势必会大量移动元素,从而影响算法的效率。
为避免上述简单转置算法中重新排序引起的元素移动,可采取接下来的两种处理方法。
3.2.1 列序递增转置法
算法思想
这里的列序指的是A的列,也就是按照A的列序来将元素转置到B中。
即将A的第一列全部转置到B中(得到B的第一行)后,再将A的第二列全部转置到B中,以此类推。
代码
//列序递增转置法
void TSMSwitch1(TSMatrix A, TSMatrix* B)
{assert(B);TSMDestroy(B);B->data = (Triple*)malloc(A.capacity * sizeof(Triple));B->capacity = A.capacity;B->len = A.len;B->m = A.n;B->n = A.m;int j = 0;//记录B当前空位for(int k = 0; k < A.n; k++){for(int i = 0; i < A.len; i++){if(A.data[i].col == k){B->data[j].row = A.data[i].col;B->data[j].col = A.data[i].row;B->data[j].e = A.data[i].e;j++;}}}
}分析
这种算法确实使得我们不用再单独进行排序,但是双重循环依然造成了较高的时间复杂度(O(A.n * A.len))。
那么我们能否降低该算法的时间复杂度呢?
如果能,那么我们的着手点一定是想办法优化掉二重循环。
可以发现,该算法中二重循环出现的原因在于,必须将A的第一列全部转置之后才能转置第二列,每列转置需要重新扫描一次A。
那么,我们有没有办法使得各列同时进行存放呢,这样就只用扫描一次A了。
3.2.2 一次定位快速转置法
算法思想
如果我们知道A的每一列有多少个元素,那么就可以推知B中每一行的起始位置。
这样一来,假如某次在A中扫描到第n列的元素,我们就可以直接将其放到B中的第n行所在位置,而不用先放完一列再放下一列。
所以,我们准备进行三次循环:
1. 定义数组num,数组的下标表示A的列,遍历A并将每一列元素的个数记录在num中。
2. 定义数组position,数组下标表示B的行,遍历position,根据A每一列元素的个数得到对应行的起始位置。
3. 遍历A,根据position数组,将A中的元素转置到B的对应行。
代码
//一次定位快速转置算法
void TSMSwitch2(TSMatrix A, TSMatrix* B)
{assert(B);TSMDestroy(B);B->data = (Triple*)malloc(A.capacity * sizeof(Triple));B->capacity = A.capacity;B->len = A.len;B->m = A.n;B->n = A.m;int num[B->m];int position[B->m];memset(num, 0, B->m * sizeof(int));memset(num, 0, B->m * sizeof(int));for(int i = 0; i < A.len; i++){num[A.data[i].col]++;}position[0] = 0;for(int row = 1; row < B->m; row++){position[row] = position[row - 1] + num[row - 1];}for(int i = 0; i < A.len; i++){B->data[position[A.data[i].col]].row = A.data[i].col;B->data[position[A.data[i].col]].col = A.data[i].row;B->data[position[A.data[i].col]].e = A.data[i].e;position[A.data[i].col]++;}
}算法分析
显然,一次定位快速转置算法的时间效率要高得多,它在时间性能上由于列序递增转置法,但在空间耗费上增加了两个辅助向量空间,即num和position。
由此可见,算法在时间上的节省是以更多的储存空间为代价的。
相关文章:

稀疏矩阵的三元组表表示法及其转置
1. 什么是稀疏矩阵 稀疏矩阵是指矩阵中大多数元素为零的矩阵。 从直观上讲,当元素个数低于总元素的30%时,这样的矩阵被称为稀疏矩阵。 由于该种矩阵的特点,我们在存储这种矩阵时,如果直接采用二维数组,就会十分浪费…...

docker安装rabbitMQ,并且创建账号
# 创建docker容器启动,挂到后台运行 docker run -d --name rabbitmq -p 5672:5672 -p 15672:15672 rabbitmq:3.13-management # 打开防火墙 sudo firewall-cmd --zonepublic --add-port5672/tcp --permanent sudo firewall-cmd --zonepublic --add-port15672/tcp --permanent s…...

wireshark解析grpc/protobuf的方法
1,wireshark需要安装3.20以上 下载地址:https://www.wireshark.org/ 2,如果版本不对,需要卸载,卸载方法: sudo rm -rf /Applications/Wireshark.app sudo rm -rf $HOME/.config/wireshark sudo rm -rf /…...
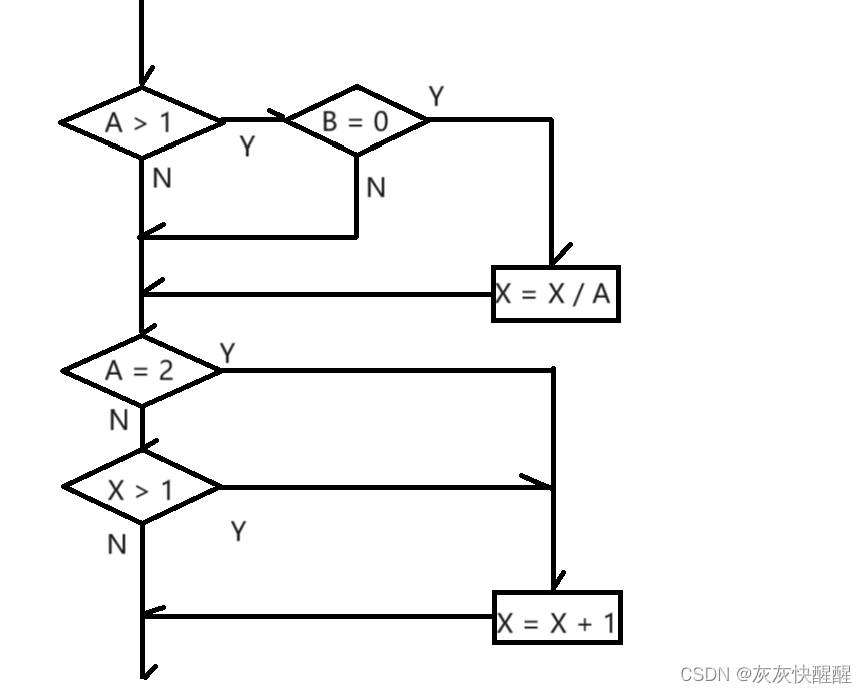
软件测试用例(2)
具体的设计方法 -- 黑盒测试 因果图 因果图是一种简化的逻辑图, 能直观地表明程序的输入条件(原因)和输出动作(结果)之间的相互关系. 因果图法是借助图形来设计测试用例的一种系统方法, 特别适用于被测试程序具有多种输入条件, 程序的输出又依赖于输入条件的各种情况. 因果图…...

集群式无人机仿真环境和数据集
仿真环境和数据集 Quick StartAcknowledgementsSwarmSim Quick Start Compiling tests passed on 20.04 with ros installed. You can just execute the following commands one by one. # Download the Simulator and run it wget https://cloud.tsinghua.edu.cn/library/34…...
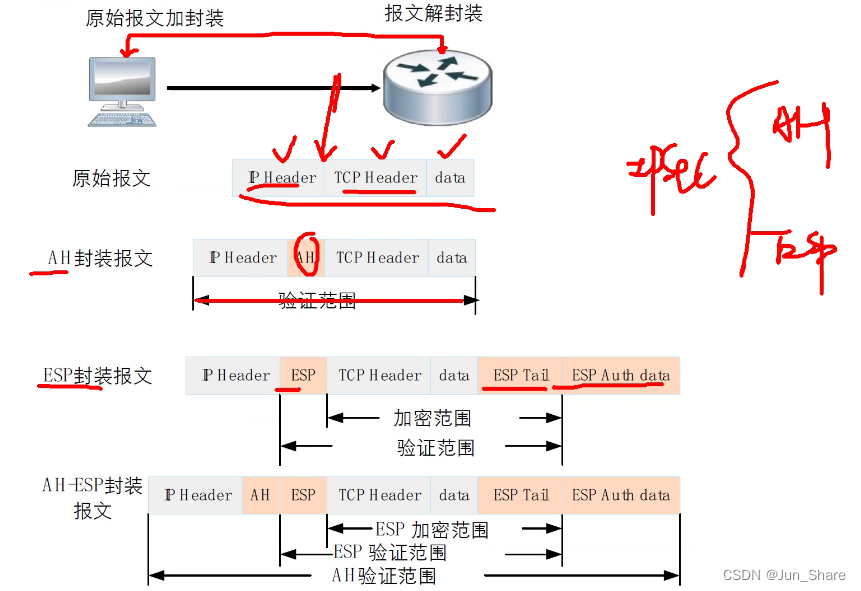
IPSec VPN
IP Security,IP安全 1、特点 L3的VPN 缺:不支持组播、配置复杂、延迟增加、资源消耗较多 优:具备访问控制、密码学四个维度、抗重放打击 2、组件 ①安全协议 1)验证头技术(AH) IP协议号51 提供数据完整性检查,身份验证,抗重放攻击 无法做数据的机密性 AH的完…...
docker部署nacos,单例模式(standalone),使用内置的derby数据库,简易安装
文章目录 前言安装创建文件夹docker指令安装docker指令安装-瘦身版 制作docker-compose.yaml文件查看页面 前言 nacos作为主流的服务发现中心和配置中心,广泛应用于springcloud框架中,现在就让我们一起简易的部署一个单例模式的nacos,版本可…...

systemd监听服务配置文件更新自动重启服务
背景&需求 需要频繁更改一个服务的配置文件进行测试 实现 配置服务的systemd文件 vim /lib/systemd/system/xxx.service [Unit] Descriptionxxx daemon, A rule-based proxy in Go.[Service] Typesimple ExecStart/opt/xxx/xxx-d /etc/xxx/ Restartalways[Install] Wan…...

【yy讲解PostCSS是如何安装和使用】
🎥博主:程序员不想YY啊 💫CSDN优质创作者,CSDN实力新星,CSDN博客专家 🤗点赞🎈收藏⭐再看💫养成习惯 ✨希望本文对您有所裨益,如有不足之处,欢迎在评论区提出…...

YOLO电动车检测识别数据集:12617张图像,yolo标注完整
YOLO电动车检测识别数据集:12617张图像,电动车一类,yolo标注完整,部分图像应用增强。 适用于CV项目,毕设,科研,实验等 需要此数据集或其他任何数据集请私信...
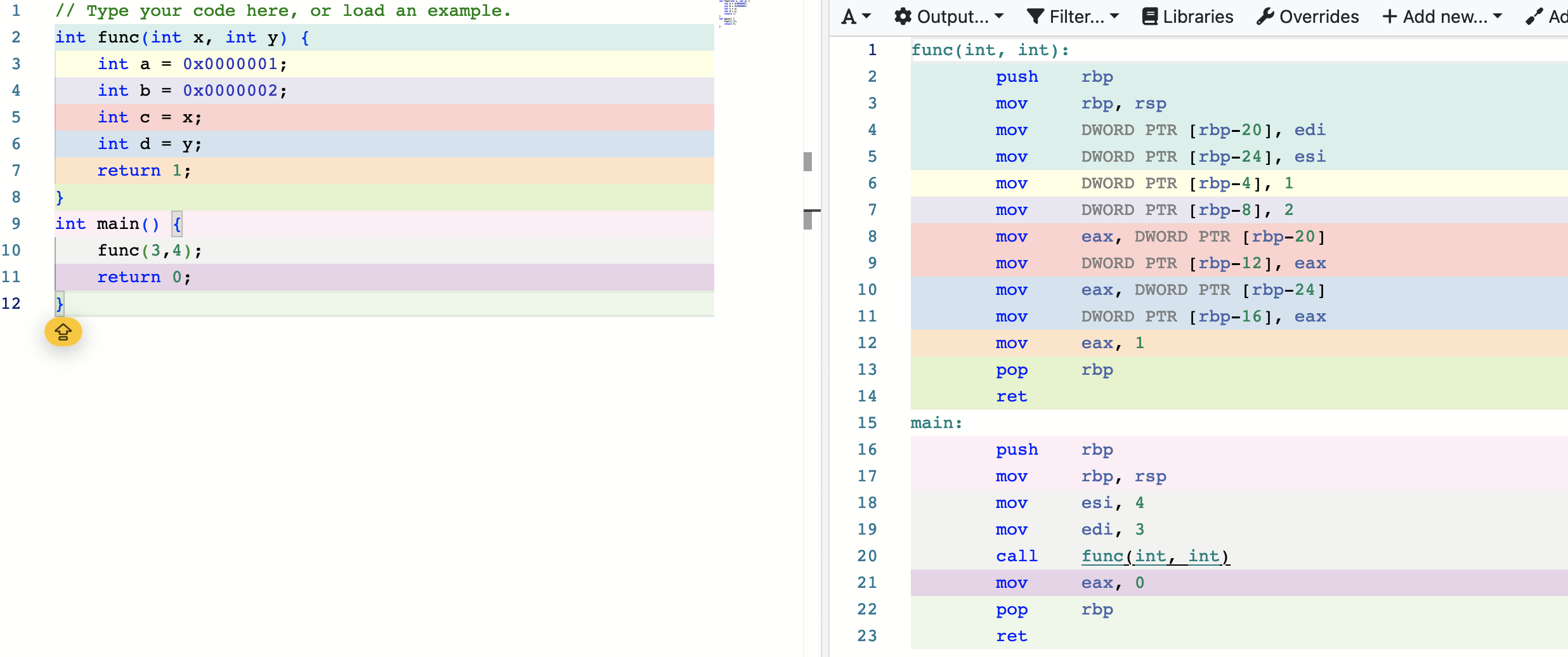
从汇编看函数调用
文章目录 函数调用流程栈相关寄存器及的作用简介寄存器功能指令功能 栈函数的括号{}正括号反括号 参数传递传值,变量不可改传指针,变量可改C 传引用 函数调用实例 函数调用流程 目标:函数调用前后栈保持不变 保存main函数的寄存器上下文移…...
node.js的错误处理
当我打开一个不存在的文件时,错误如下: 在读取文件里面写入console.log(err),在控制台中可以看到我的错误代码类型:文件不存在的错误代码 ENOENT。见更多错误代码---打开node.js官方API文档Error 错误 | N…...
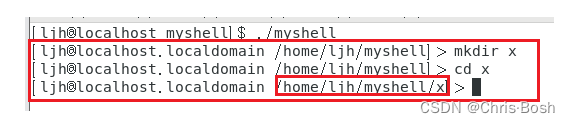
shell的编写
文章目录 1.框架2.命令行3.获取用户命令字符串4.命令行字符串分割5.执行命令和内建命令6.完整代码: 1.框架 我们知道shell是一直存在的,所以首先我们第一步就是要搭建一个框架,使其一直存在。 那么也很简单,一个while循环就可以完…...

css心跳动画
图标引入 <img class"icon" src"heart.svg" alt"" srcset""> CSS代码 <style>.icon {animation:bpm 1s linear,pulse 0.75s 1s linear infinite;}keyframes pulse {from,75%,to {transform: scale(1);}25% {transform:…...

在 Amazon Timestream 上通过时序数据机器学习进行预测分析
由于不断变化的需求和现代化基础设施的动态性质,为大型应用程序规划容量可能会非常困难。例如,传统的反应式方法依赖于某些 DevOps 指标(如 CPU 和内存)的静态阈值,而这些指标在这样的环境中并不足以解决问题。在这篇文…...

【智能排班系统】快速消费线程池
文章目录 线程池介绍线程池核心参数核心线程数(Core Pool Size)最大线程数(Maximum Pool Size)队列(Queue)线程空闲超时时间(KeepAliveTime)拒绝策略(RejectedExecutionH…...
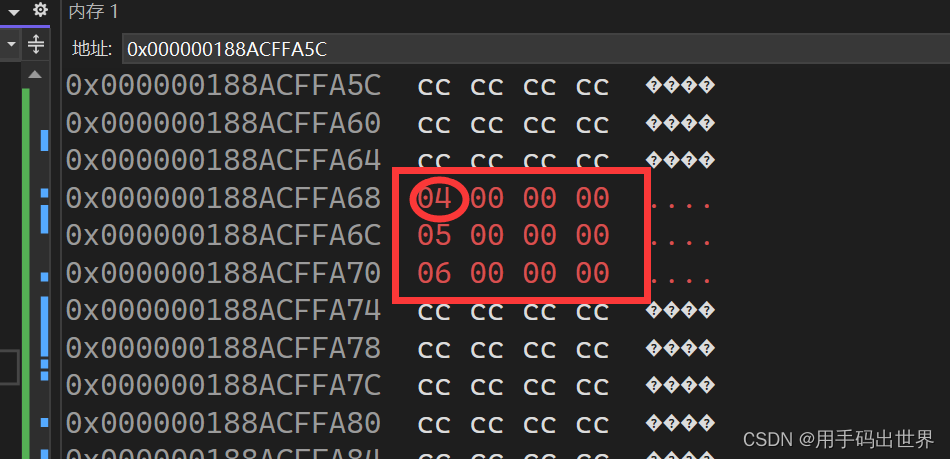
C语言——内存函数
前言: C语言中除了字符串函数和字符函数外,还有一些函数可以直接对内存进行操作,这些函数被称为内存函数,这些函数与字符串函数都属于<string.h>这个头文件中。 一.memcpy()函数 memcpy是C语言中的…...
ideaSSM图书借阅管理系统VS开发mysql数据库web结构java编程计算机网页源码maven项目
一、源码特点 SSM 图书借阅管理系统是一套完善的信息管理系统,结合SSM框架和bootstrap完成本系统,对理解JSP java编程开发语言有帮助系统采用SSM框架(MVC模式开发),系统具有完整的源代码 和数据库,系统主…...
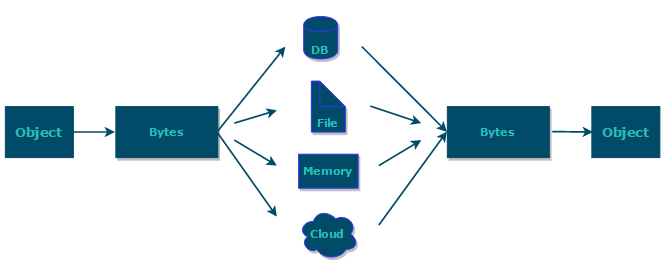
普联一面4.2面试记录
普联一面4.2面试记录 文章目录 普联一面4.2面试记录1.jdk和jre的区别2.java的容器有哪些3.list set map的区别4.get和post的区别5.哪个更安全6.java哪些集合类是线程安全的7.创建线程有哪几种方式8.线程的状态有哪几种9.线程的run和start的区别10.什么是java序列化11.redis的优…...
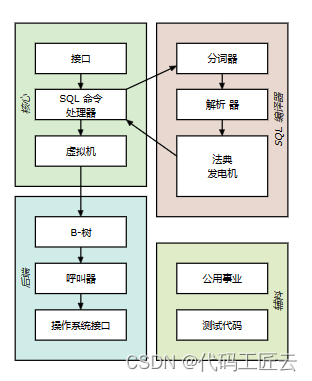
SQLite的架构(十一)
返回:SQLite—系列文章目录 上一篇:SQLite下一代查询规划器(十) 下一篇:SQLite—系列文章目录 介绍 本文档介绍SQLite库的架构。 这里的信息对那些想要了解或 修改SQLite的内部工作原理。 接口SQL 命令处理器虚拟机B-树…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

python执行测试用例,allure报乱码且未成功生成报告
allure执行测试用例时显示乱码:‘allure’ �����ڲ����ⲿ���Ҳ���ǿ�&am…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

【p2p、分布式,区块链笔记 MESH】Bluetooth蓝牙通信 BLE Mesh协议的拓扑结构 定向转发机制
目录 节点的功能承载层(GATT/Adv)局限性: 拓扑关系定向转发机制定向转发意义 CG 节点的功能 节点的功能由节点支持的特性和功能决定。所有节点都能够发送和接收网格消息。节点还可以选择支持一个或多个附加功能,如 Configuration …...
