补代码随想录算法训练营第44天 | 完全背包、518. 零钱兑换 II 、377. 组合总和 Ⅳ
完全背包
视频讲解：带你学透完全背包问题！ 和 01背包有什么差别？遍历顺序上有什么讲究？_哔哩哔哩_bilibili
https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.html
518. 零钱兑换 II
视频讲解：动态规划之完全背包，装满背包有多少种方法？组合与排列有讲究！| LeetCode：518.零钱兑换II_哔哩哔哩_bilibili
代码随想录
377. 组合总和 Ⅳ
视频讲解：动态规划之完全背包，装满背包有几种方法？求排列数？| LeetCode：377.组合总和IV_哔哩哔哩_bilibili
代码随想录
相关文章：
补代码随想录算法训练营第44天 | 完全背包、518. 零钱兑换 II 、377. 组合总和 Ⅳ
完全背包 视频讲解：带你学透完全背包问题！ 和 01背包有什么差别？遍历顺序上有什么讲究？_哔哩哔哩_bilibili https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5…...
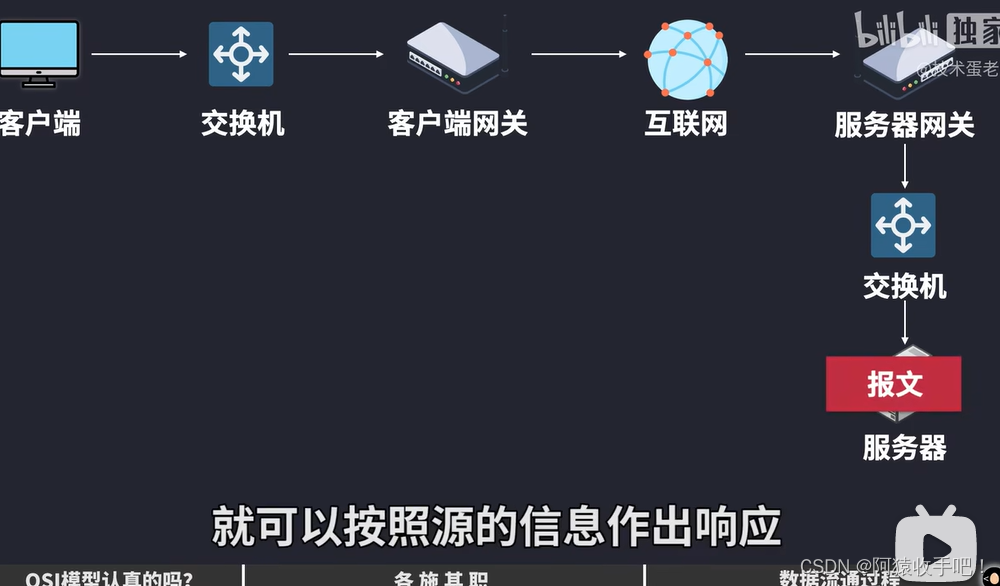
【Linux】网络基础常识{OSI七层模型/ TCP/IP / 端口号 /各种协议}
文章目录 1.网络常识1.0DHCP协议1. 1IP地址/MAC地址/ARP协议是什么？IP/MACARP：IP ⇒ MAC 1.2手机连接wifi的原理 SSID与BSSID手机连接wifiSSID与BSSID 1.3手机如何通过“数据/流量”上网？1.4电脑连接wifi的原理？电脑通过热点上网…...
python--面向对象编程和类的定义，对象的创建
一、面向对象简介 1、什么是面向对象 面向对象是一种编程思想，把数据和对数据的多个操作方法封装在一起组成类，这样通过这个类创建出来的对象,就可以直接调用这些方法了。 2、面向对象相关的术语 类：用来描述具有相同的属性和方法的对象的…...
nssm 工具把asp.net core mvc变成 windows服务，使用nginx反向代理访问
nssm工具的作用：把项目部署成Windows服务，可以在系统后台运行 1.创建一个asp.net core mvc的项目weblication1 asp.net core mvc项目要成为windows服务需要安装下面的nuget包 <ItemGroup><PackageReference Include"Microsoft.Extension…...
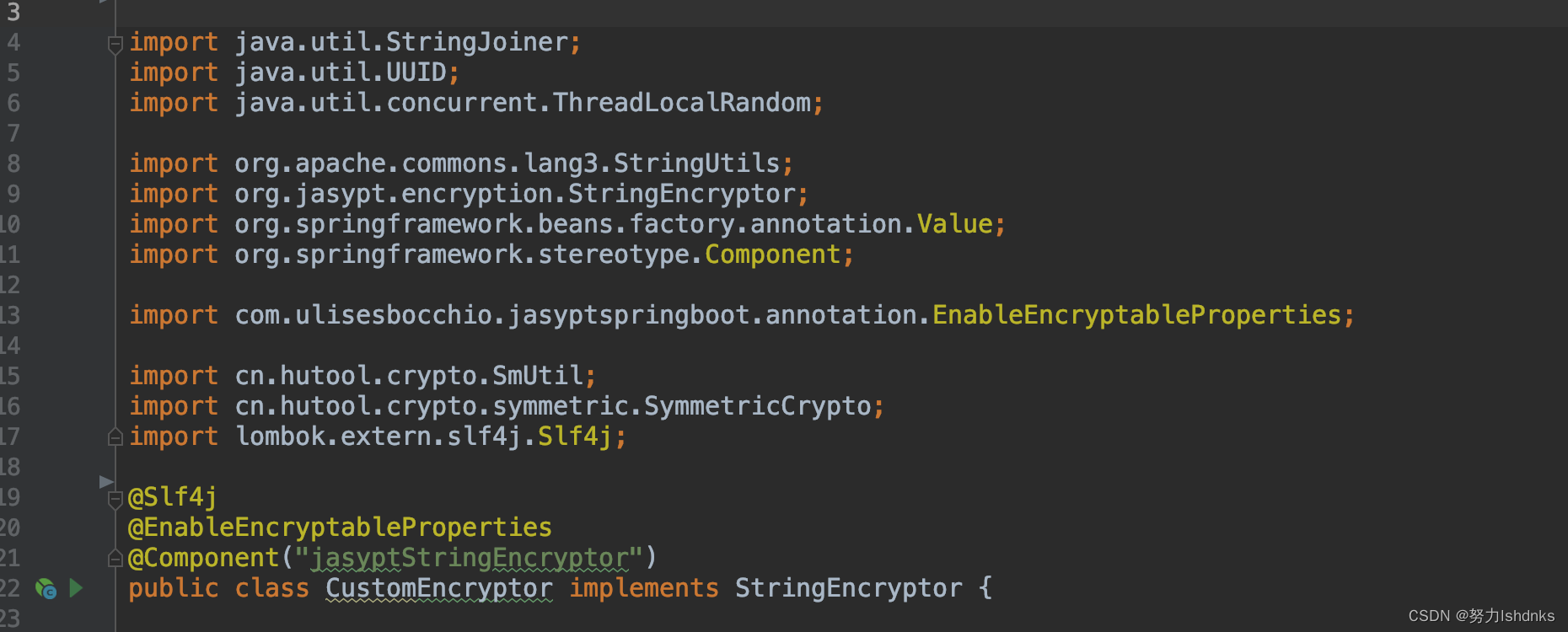
String Encryptor custom Bean not found with name ‘jasyptStringEncryptor‘...
项目采用 spring boot 2.6.13 jasypt-spring-boot-starter 3.0.5 apollo-client 1.6.0 自定义jasyptStringEncryptor，服务器上启动死活报找不到bean jasyptStringEncryptor，采用默认的，密文配置项自然解密失败导致服务无法启动。 经过一…...
FastAPI+React全栈开发14 FastAPI如何开发REST接口
Chapter03 Getting Started with FastAPI 14 How does FastAPI speak REST FastAPIReact全栈开发14 FastAPI如何开发REST接口 Let’s create a minial FastAPI application, a classic Hello World example, and start examining how FastAPI structures the endpoints. I u…...
在 DDD 中，如何处理领域对象的持久化？
在 DDD 中，领域对象的持久化工作通常是通过仓库 Repository 和工厂 Factory 实现的。仓库是一种用于访问领域对象的机制。他负责将领域对象从内存中保存到持久存储，如数据库中，以及从持久存储中检索领域对象。而工厂则负责从持久存储中组装领…...
centos 如何安装nvidia-container-runtime
在CentOS上安装nvidia-container-runtime，首先需要确保你的系统已经安装了NVIDIA的驱动和docker。以下是安装步骤： 确保Docker已安装： sudo yum install -y yum-utils sudo yum-config-manager --add-repo https://download.docker.com/lin…...
非写代码无以致远
标题党一下，本篇文章主要汇总了一些代码题，让大家写一些代码练习一下吧！ 变种水仙花_牛客题霸_牛客网 (nowcoder.com) #include<stdio.h> int main() {for (int i 10000; i < 99999; i) {int sum 0;for (int j 10; j < 1000…...
刷题之Leetcode34题(超级详细)
34. 在排序数组中查找元素的第一个和最后一个位置 力扣链接(opens new window)https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/ 给定一个按照升序排列的整数数组 nums，和一个目标值 target。找出给定目标值在数组中的开始…...
从0到1构建uniapp应用-store状态管理
背景 在 UniApp的开发中，状态管理的目标是确保应用数据的一致性，提升用户体验，并简化开发者的工作流程。通过合理的状态管理，可以有效地处理用户交互、数据同步和界面更新等问题。 此文主要用store来管理用户的登陆信息。 重要…...
Uinx线程详解
目录 一.什么是线程？ 并发（Concurrency） 并行（Parallelism） 1.1 线程的概念 1.2 线程的基本函数 1.3 线程的基本使用例子： 二.线程的属性 2.1线程属性使用例子 三.线程互斥 3.1互斥锁 3.2互斥锁常用函…...
线性代数笔记23--马尔可夫矩阵、傅里叶级数
1. 马尔可夫矩阵 例子 A [ . 1 . 001 . 3 . 2 . 099 . 3 . 7 0 . 4 ] A \begin{bmatrix} .1 & .001 & .3\\ .2 & .099 & .3\\ .7 & 0 & .4 \end{bmatrix} A .1.2.7.001.0990.3.3.4 马尔可夫矩阵满足条件 λ 1 为特征值 \lambda1为特征…...
Elasticsearch 压测实践总结
背景 搜索、ES运维场景离不开压力测试。 1.宿主机层面变更：参数调优 & 配置调整 & 硬件升级2.集群层面变更：参数调优3.索引层面变更：mapping调整 当然还有使用层面变更，使用API调优（不属于该文章的讨论范围…...
Spirngboot JWT快速配置和使用
2、JWT 2.1、JWT介绍 JWT是JSON Web Token的缩写，即JSON Web令牌，是一种自包含令牌。 是为了在网络应用环境间传递声明而执行的一种基于JSON的开放标准。 JWT的声明一般被用来在身份提供者和服务提供者间传递被认证的用户身份信息，以便于从…...
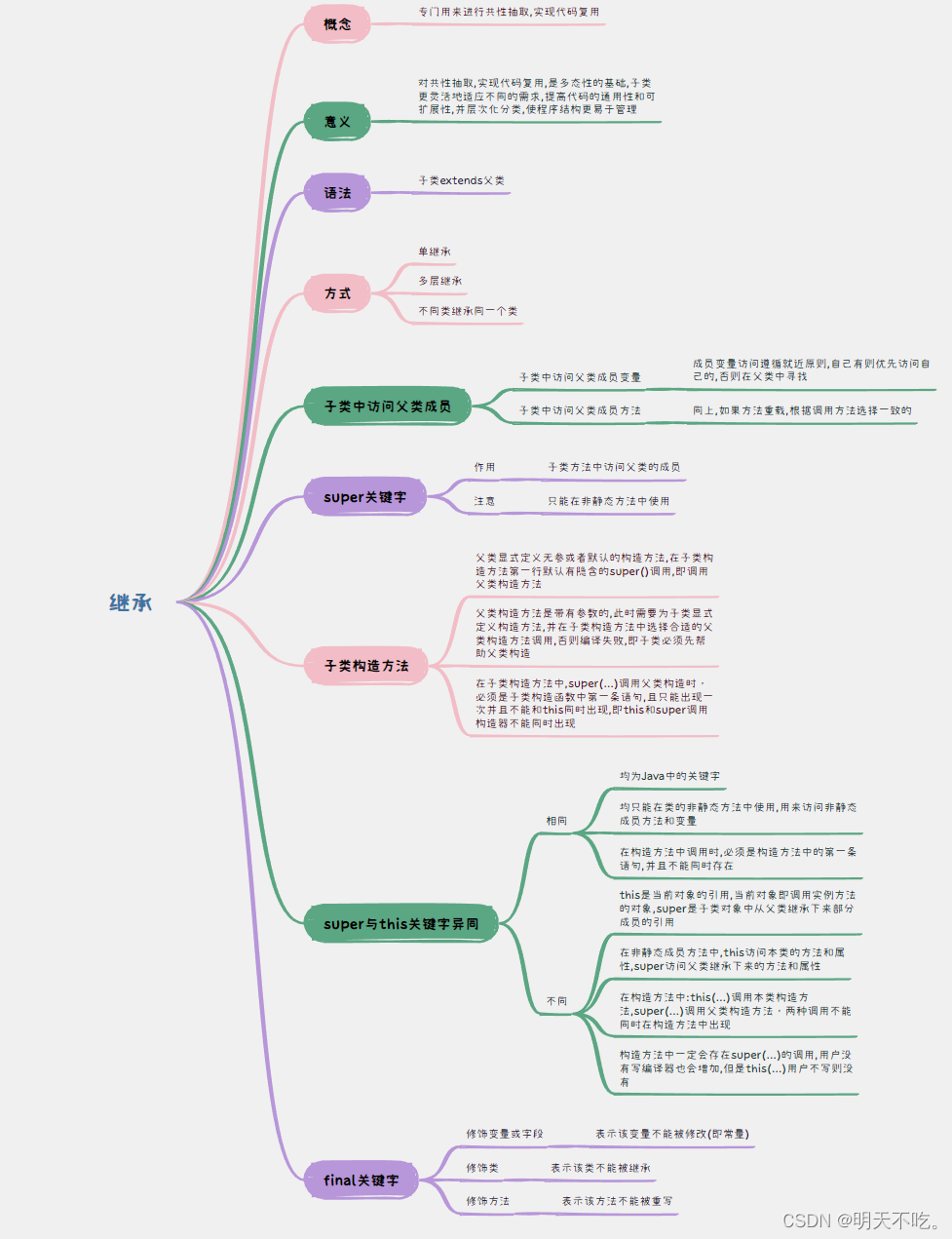
【Java SE】继承
🥰🥰🥰来都来了，不妨点个关注叭！ 👉博客主页：欢迎各位大佬!👈 文章目录 1. 继承1.1 继承是什么1.2 继承的意义1.3 继承的语法1.4 继承的方式1.5 子类中访问父类成员1.5.1 子类中访问…...
：策略模式)
设计模式(19)：策略模式
策略模式 策略模式对应与解决某一个问题的一个算法族，允许用户从该算法族中任选一个算法解决某一问题，同时可以方便的更换算法或者增加新的算法。并且由客户端决定调用哪个算法。 本质 分离算法，选择实现； 策略模式角色 上下…...
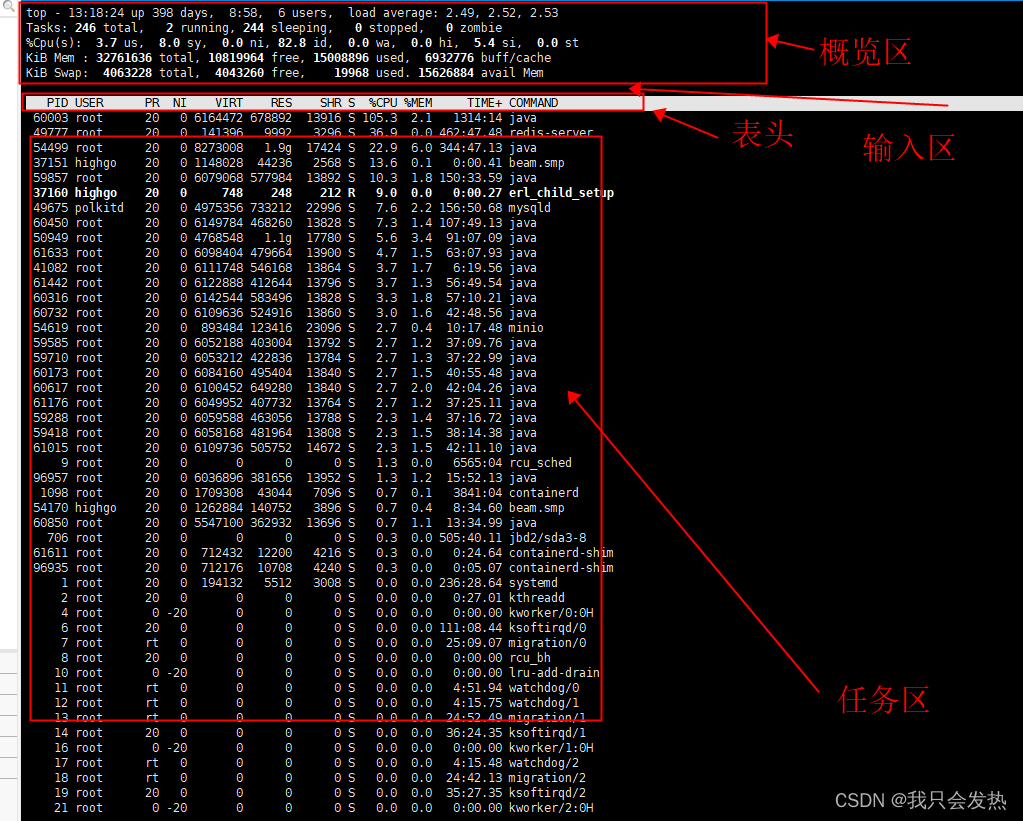
Linux 命令 top 详解
1 top命令介绍 Linux系统中，Top命令主要用于实时运行系统的监控，包括Linux内核管理的进程或者线程的资源占用情况。这个命令对所有正在运行的进程和系统负荷提供不断更新的概览信息，包括系统负载、CPU利用分布情况、内存使用、每个进程的内容…...
Android安卓开发 - 简单介绍（一）
最近呢需要重构还有维护安卓项目，所以最近会从零开始梳理开发的一些知识点以及开发的内容 前面已经写了安装的教程，idea怎么安装，还有官方的开发工具Android Studio怎么安装 2024最新版Android studio安装入门教程（非常详细&…...
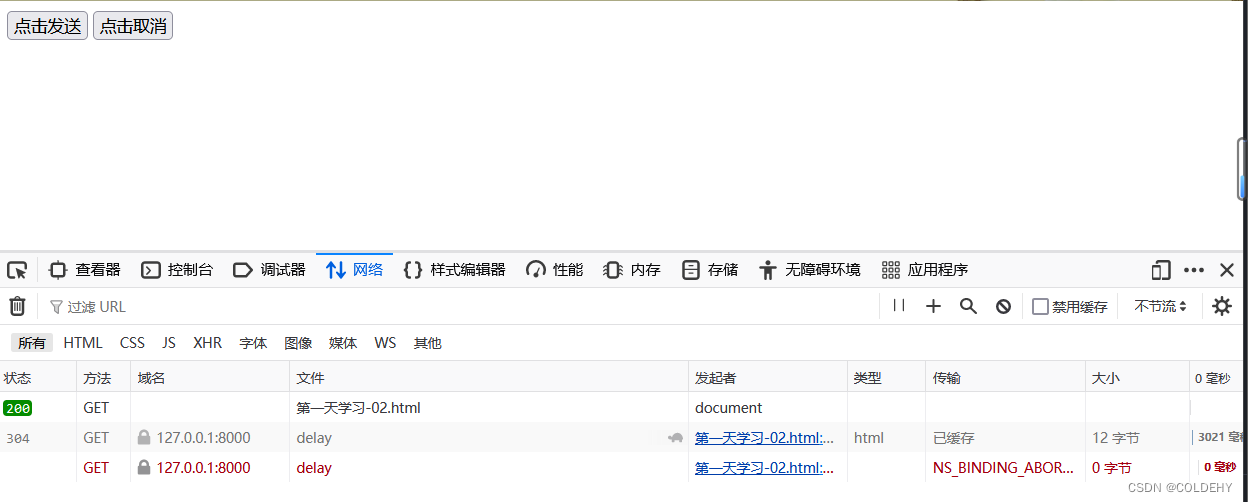
AJAX —— 学习（二）
目录 一、利用 JSON 字符串 返回数据 （一）基础代码 （二）原理及实现 二、nodmon 工具 自动重启服务 （一）用途 （二）下载 （三）使用 三、IE 缓存问题 &a…...
基于FPGA的PID算法学习———实现PID比例控制算法
基于FPGA的PID算法学习 前言一、PID算法分析二、PID仿真分析1. PID代码2.PI代码3.P代码4.顶层5.测试文件6.仿真波形 总结 前言 学习内容：参考网站： PID算法控制 PID即：Proportional（比例）、Integral（积分&…...
可靠性+灵活性：电力载波技术在楼宇自控中的核心价值
可靠性灵活性：电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中，电力载波技术（PLC）凭借其独特的优势，正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据，无需额外布…...
LeetCode - 394. 字符串解码
题目 394. 字符串解码 - 力扣（LeetCode） 思路 使用两个栈：一个存储重复次数，一个存储字符串 遍历输入字符串： 数字处理：遇到数字时，累积计算重复次数左括号处理：保存当前状态&a…...
Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名（Class Name)2.协议名（Protocol Name)3.方法名（Method Name)4.属性名（Property Name）5.局部变量/实例变量（Local / Instance Variables&…...
vue3 字体颜色设置的多种方式
在Vue 3中设置字体颜色可以通过多种方式实现，这取决于你是想在组件内部直接设置，还是在CSS/SCSS/LESS等样式文件中定义。以下是几种常见的方法： 1. 内联样式 你可以直接在模板中使用style绑定来设置字体颜色。 <template><div :s…...
P3 QT项目----记事本（3.8）
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...
ETLCloud可能遇到的问题有哪些？常见坑位解析
数据集成平台ETLCloud，主要用于支持数据的抽取（Extract）、转换（Transform）和加载（Load）过程。提供了一个简洁直观的界面，以便用户可以在不同的数据源之间轻松地进行数据迁移和转换。…...
Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统，支持多语言对话（如 中文，英文，日语），语音情感（如 开心，悲伤）&#x…...
【OSG学习笔记】Day 16: 骨骼动画与蒙皮（osgAnimation）
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术，它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton)：由层级结构的骨头组成，类似于人体骨骼蒙皮 (Mesh Skinning)：将模型网格顶点绑定到骨骼上，使骨骼移动…...
在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...