Python从0到100(十):Python集合介绍及运用

一、集合定义
定义: 由不同元素组成的集合,集合是一组无序排列 可hash值,可作为字典的key。
特性: 集合的目的是将不同的值存放在一起,不同的集合间用来做关系运算,无须纠结于集合中的单个值。
(1、不同元素组成 2、无序 3、集合中的元素必须是不可变类型)
二、创建集合
在Python中,创建集合可以使用{}字面量语法,{}中需要至少有一个元素,因为没有元素的{}并不是空集合而是一个空字典,我们下一节课就会大家介绍字典的知识。当然,也可以使用内置函数set来创建一个集合,准确的说set并不是一个函数,而是创建集合对象的构造器,这个知识点我们很快也会讲到,现在不理解跳过它就可以了。要创建空集合可以使用set();也可以将其他序列转换成集合,例如:set('hello')会得到一个包含了4个字符的集合(重复的l会被去掉)。除了这两种方式,我们还可以使用生成式语法来创建集合,就像我们之前用生成式创建列表那样。要知道集合中有多少个元素,还是使用内置函数len;使用for循环可以实现对集合元素的遍历。
# 创建集合的字面量语法(重复元素不会出现在集合中)
set1 = {1, 2, 3, 3, 3, 2}
print(set1) # {1, 2, 3}
print(len(set1)) # 3# 创建集合的构造器语法(后面会讲到什么是构造器)
set2 = set('hello')
print(set2) # {'h', 'l', 'o', 'e'}# 将列表转换成集合(可以去掉列表中的重复元素)
set3 = set([1, 2, 3, 3, 2, 1])
print(set3) # {1, 2, 3}# 创建集合的生成式语法(将列表生成式的[]换成{})
set4 = {num for num in range(1, 20) if num % 3 == 0 or num % 5 == 0}
print(set4) # {3, 5, 6, 9, 10, 12, 15, 18}# 集合元素的循环遍历
for elem in set4:print(elem)
需要提醒大家,集合中的元素必须是hashable类型。所谓hashable类型指的是能够计算出哈希码的数据类型,大家可以暂时将哈希码理解为和变量对应的唯一的ID值。通常不可变类型都是hashable类型,如整数、浮点、字符串、元组等,而可变类型都不是hashable类型,因为可变类型无法确定唯一的ID值,所以也就不能放到集合中。集合本身也是可变类型,所以集合不能够作为集合中的元素,这一点在使用集合的时候一定要注意。
三、集合的运算
Python为集合类型提供了非常丰富的运算符,主要包括:成员运算、交集运算、并集运算、差集运算、比较运算(相等性、子集、超集)等。
1.成员运算
可以通过成员运算in和not in 检查元素是否在集合中,代码如下所示。
set1 = {11, 12, 13, 14, 15}
print(10 in set1) # False
print(15 in set1) # True
set2 = {'Python', 'Java', 'Go', 'Swift'}
print('Ruby' in set2) # False
print('Java' in set2) # True
2.交并差运算
Python中的集合跟数学上的集合一样,可以进行交集、并集、差集等运算,而且可以通过运算符和方法调用两种方式来进行操作,代码如下所示。
set1 = {1, 2, 3, 4, 5, 6, 7}
set2 = {2, 4, 6, 8, 10}# 交集
# 方法一: 使用 & 运算符
print(set1 & set2) # {2, 4, 6}
# 方法二: 使用intersection方法
print(set1.intersection(set2)) # {2, 4, 6}# 并集
# 方法一: 使用 | 运算符
print(set1 | set2) # {1, 2, 3, 4, 5, 6, 7, 8, 10}
# 方法二: 使用union方法
print(set1.union(set2)) # {1, 2, 3, 4, 5, 6, 7, 8, 10}# 差集
# 方法一: 使用 - 运算符
print(set1 - set2) # {1, 3, 5, 7}
# 方法二: 使用difference方法
print(set1.difference(set2)) # {1, 3, 5, 7}# 对称差
# 方法一: 使用 ^ 运算符
print(set1 ^ set2) # {1, 3, 5, 7, 8, 10}
# 方法二: 使用symmetric_difference方法
print(set1.symmetric_difference(set2)) # {1, 3, 5, 7, 8, 10}
# 方法三: 对称差相当于两个集合的并集减去交集
print((set1 | set2) - (set1 & set2)) # {1, 3, 5, 7, 8, 10}
集合的交集、并集、差集运算还可以跟赋值运算一起构成复合赋值运算,如下所示。
set1 = {1, 3, 5, 7}
set2 = {2, 4, 6}
# 将set1和set2求并集再赋值给set1
# 也可以通过set1.update(set2)来实现
set1 |= set2
print(set1) # {1, 2, 3, 4, 5, 6, 7}
set3 = {3, 6, 9}
# 将set1和set3求交集再赋值给set1
# 也可以通过set1.intersection_update(set3)来实现
set1 &= set3
print(set1) # {3, 6}
3.比较运算
两个集合可以用==和!=进行相等性判断,如果两个集合中的元素完全相同,那么==比较的结果就是True,否则就是False。如果集合A的任意一个元素都是集合B的元素,那么集合A称为集合B的子集,即对于$ \forall{a} \in {A} ,均有 ,均有 ,均有 {a} \in {B} ,则 ,则 ,则 {A} \subseteq {B} $,A是B的子集,反过来也可以称B是A的超集。如果A是B的子集且A不等于B,那么A就是B的真子集。Python为集合类型提供了判断子集和超集的运算符,其实就是我们非常熟悉的<和>运算符,代码如下所示。
set1 = {1, 3, 5}
set2 = {1, 2, 3, 4, 5}
set3 = set2
# <运算符表示真子集,<=运算符表示子集
print(set1 < set2, set1 <= set2) # True True
print(set2 < set3, set2 <= set3) # False True
# 通过issubset方法也能进行子集判断
print(set1.issubset(set2)) # True# 反过来可以用issuperset或>运算符进行超集判断
print(set2.issuperset(set1)) # True
print(set2 > set1) # True
四、集合的方法
Python中的集合是可变类型,我们可以通过集合类型的方法为集合添加或删除元素。
1.创建一个空集合
# 创建一个空集合
set1 = set()
2.通过add方法添加元素
set1.add(33)
set1.add(55)
set1.update({1, 10, 100, 1000})
print(set1) # {33, 1, 100, 55, 1000, 10}
3.通过discard方法删除指定元素
# 通过discard方法删除指定元素
set1.discard(100)
set1.discard(99)
print(set1) # {1, 10, 33, 55, 1000}
4.通过remove方法删除指定元素
# 通过remove方法删除指定元素
# 否则元素如果不在集合中就会引发KeyError异常
if 10 in set1:set1.remove(10)
print(set1) # {33, 1, 55, 1000}
5.pop方法
pop方法可以从集合中随机删除一个元素并返回该元素
# pop方法可以从集合中随机删除一个元素并返回该元素
print(set1.pop())
6.clear方法
clear方法可以清空整个集合
# clear方法可以清空整个集合
set1.clear()
print(set1) # set()
如果要判断两个集合有没有相同的元素可以使用isdisjoint方法,没有相同元素返回True,否则返回False,代码如下所示。
set1 = {'Java', 'Python', 'Go', 'Kotlin'}
set2 = {'Kotlin', 'Swift', 'Java', 'Objective-C', 'Dart'}
set3 = {'HTML', 'CSS', 'JavaScript'}
print(set1.isdisjoint(set2)) # False
print(set1.isdisjoint(set3)) # True
五、不可变集合
Python中还有一种不可变类型的集合,名字叫frozenset。set跟frozenset的区别就如同list跟tuple的区别,frozenset由于是不可变类型,能够计算出哈希码,因此它可以作为set中的元素。除了不能添加和删除元素,frozenset在其他方面跟set基本是一样的,下面的代码简单的展示了frozenset的用法。
set1 = frozenset({1, 3, 5, 7})
set2 = frozenset(range(1, 6))
print(set1 & set2) # frozenset({1, 3, 5})
print(set1 | set2) # frozenset({1, 2, 3, 4, 5, 7})
print(set1 - set2) # frozenset({7})
print(set1 < set2) # False
集合是一种容器,元素必须是hashable类型,与列表不同的地方在于集合中的元素没有序、不能用索引运算、不能重复。
相关文章:

Python从0到100(十):Python集合介绍及运用
一、集合定义 定义: 由不同元素组成的集合,集合是一组无序排列 可hash值,可作为字典的key。 特性: 集合的目的是将不同的值存放在一起,不同的集合间用来做关系运算,无须纠结于集合中的单个值。 ࿰…...
实用技巧:如何取消app的截屏禁用
因为我想要在小鹅通App做笔记,但是被小鹅通App禁用截屏了,这真是一个很糟糕的使用体验,虽然可能是为了保护商家权益…… 方法1 可以让商家设置课程可以截屏 方法2 手机root,安装Xposed框架,利用Xposed框架上面的插件我们可以对手机进行高度定制化,而安装Xposed框架的…...
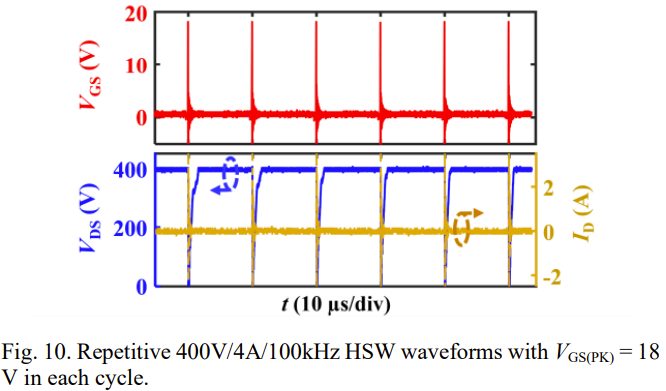
【氮化镓】GaN SP-HEMT的栅极可靠性
概括总结: 本文研究了氮化镓(GaN)肖特基型p-栅高电子迁移率晶体管(GaN SP-HEMT)的栅极鲁棒性和可靠性,通过一种新的电路方法评估了在实际转换器中栅极电压(VGS)过冲波形的栅极电压应…...

Linux基础和进阶用法
Linux是一个广泛使用的开源操作系统,下面是一些Linux基础用法的详细介绍:文件和目录操作:ls:列出文件和目录的详细信息,包括权限、所有者、大小等。cd:切换到指定目录。使用cd ~返回用户主目录,…...

Linux运维-SHELL编程之正则表达式与流编辑处理器
Linux运维-SHELL编程之正则表达式与流编辑处理器 什么是正则表达式 正则表达式是一种用来描述字符序列的强大工具,通常用于字符串的匹配、搜索和替换操作。它由普通字符(例如字母、数字)和特殊字符(称为元字符)组成&…...

openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint
文章目录 openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint256.1 功能描述256.2 语法格式256.3 参数说明 openGauss学习笔记-256 openGauss性能调优-使用Plan Hint进行调优-优化器GUC参数的Hint 256.1 功能描述 设置本次查询执行内生效的…...

flex:1的作用是什么?
占满剩余的高度 <div classfather><div classson1></div><div classson2></div> </div>当给father添加display:flex之后,假设给son2添加flex:1,那么son2将会占满除son1之外的高度...

Mysql安装(命令方式安装)
下载mysql压缩包 Mysql可以使用界面安装,也可以使用命令的方式安装,今天我们使用命令的方式安装mysql。首先下载mysql压缩包(下载地址:https://dev.mysql.com/downloads/mysql/),解压到你想要安装的目录。 …...
)
Vben Admin实战-系统管理之用户管理-(第12节)
系列文章目录 第一节:Vben Admin介绍和初次运行 第二节:Vben Admin 登录逻辑梳理和对接后端准备 第三节:Vben Admin登录对接后端login接口 第四节:Vben Admin登录对接后端getUserInfo接口 第五节:Vben Admin权限-前端控制方式 第六节:Vben Admin权限-后端控制方式 第七节…...

Oracle常规操作
1、查看用户和密码 select username,password from dba_users; --修改用户和密码 alter user system identified by manager; alter user system identified by values 2D594E86F93B17A1; --解锁用户 alter user system account unlock; -- 用SYSDBA身份进入数据库,然…...

「33」如何让你的直播场景增加透视感?
「33」模糊滤镜增强背景画面透视感 在直播中,背景一直是作为一种陪衬而存在的,位于主场景的后面,其实,说得更直白一些,背景的存在就犹如“绿叶”,是为了衬托红花更加艳丽。所以…… 你通过画面背景的调整,可以从整体上对视频或图片的画面进行装饰,有助于增加画面的空间…...
Macbook文件清理软件 Mac电脑清理垃圾文件怎么清理
为了维护Macbook电脑的系统健康,我们需要定期给电脑进行全面清理,清除系统垃圾文件、软件缓存和系统内存。那么好用的Macbook文件清理软件有哪些呢?今天就给大家介绍几款好用的电脑清理软件并介绍Mac电脑清理垃圾文件怎么清理。 一、Macbook…...

【Java基础】Java基础知识整合
文章目录 1. 转义字符2. 变量2.1 字符串与整型相加2.2 byte和short的区别2.3 float和double的区别2.4 char类型2.5 boolean类型2.6 自动类型转换及运算2.7 强制类型转换2.8 String的转换2.9 除法运算2.10 取模规则 3. 自增4. 逻辑运算符5. 赋值运算 6. 三元运算符:7…...
)
构建集创建、售卖、转让于一体,且基于ERC721 token的NFT平台,从编写智能合约开始(Web3项目四实战之一)
NFT 全称是 non-fungible token(非同质化代币或不可篡改代币)是记录在区块链上的唯一数字标识符,用于证明所有权和真实性。NFT 的所有权记录在区块链中,所有者可以转让,从而允许 NFT 出售和交易。任何人都可以创建 NFT,创建 NFT 几乎不需要任何编码技能。NFT 通常包含对艺…...

跨境金融区块链服务平台
跨境金融服务是因企业及个人跨境经营、交易、投资、往来等活动而产生的资金使用、调拨、配置等需求,而提供的金融服务。近年来,随着我国经济的快速稳步增长和全球化经济一体化的不断深入发展,跨境金融业务增长迅速,监管也开始转化…...

运筹学经典问题(八):CVRP和VRP-TW
文章目录 问题描述问题建模决策变量数学建模基于容量的消除子环的约束 (load-based SECs) CVRP完整的数学模型加上时间窗限制的CVRP 问题描述 给定一个图,图上的点代表客户,边代表客户之间的路线,边的权重代表客户之间…...
)
AI与技术美术(TechArt)
AI技术与TA 人工智能(AI)技术在技术美术(TechArt)领域的应用,为创业者开辟了一片新的天地。技术美术作为一个跨学科领域,融合了传统美术和现代技术,特别是AI技术,以创造新型的艺术表…...
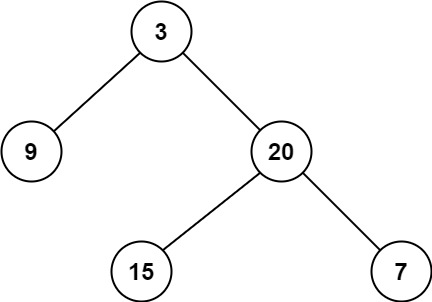
二叉树层序遍历 及相关题目
1,力扣102 给你二叉树的根节点 root ,返回其节点值的 层序遍历 。 (即逐层地,从左到右访问所有节点)。 示例 1: 输入:root [3,9,20,null,null,15,7] 输出:[[3],[9,20],[15,7]]示例…...

【前端面试3+1】11 http和https有何不同及https的加密过程、数组有哪些方法及作用、tcp三次握手四次挥手、【分发饼干】
一、http和https有何不同?https的加密过程 1、不同: HTTP和HTTPS的主要区别在于安全性。HTTP是超文本传输协议,是一种用于传输数据的协议,但是传输的数据是明文的,容易被窃听和篡改。而HTTPS是在HTTP基础上加入了SSL/T…...
替代 Redis 和 Memcached:25 倍吞吐量! | 开源日报 No.213
dragonflydb/dragonfly Stars: 22.4k License: NOASSERTION Dragonfly 是一个内存数据存储,适用于现代应用工作负载,可替代 Redis 和 Memcached。与传统的内存数据存储相比,Dragonfly 提供了 25 倍的吞吐量、更高的缓存命中率和更低尾部延…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

转转集团旗下首家二手多品类循环仓店“超级转转”开业
6月9日,国内领先的循环经济企业转转集团旗下首家二手多品类循环仓店“超级转转”正式开业。 转转集团创始人兼CEO黄炜、转转循环时尚发起人朱珠、转转集团COO兼红布林CEO胡伟琨、王府井集团副总裁祝捷等出席了开业剪彩仪式。 据「TMT星球」了解,“超级…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

高防服务器能够抵御哪些网络攻击呢?
高防服务器作为一种有着高度防御能力的服务器,可以帮助网站应对分布式拒绝服务攻击,有效识别和清理一些恶意的网络流量,为用户提供安全且稳定的网络环境,那么,高防服务器一般都可以抵御哪些网络攻击呢?下面…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

抽象类和接口(全)
一、抽象类 1.概念:如果⼀个类中没有包含⾜够的信息来描绘⼀个具体的对象,这样的类就是抽象类。 像是没有实际⼯作的⽅法,我们可以把它设计成⼀个抽象⽅法,包含抽象⽅法的类我们称为抽象类。 2.语法 在Java中,⼀个类如果被 abs…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

LCTF液晶可调谐滤波器在多光谱相机捕捉无人机目标检测中的作用
中达瑞和自2005年成立以来,一直在光谱成像领域深度钻研和发展,始终致力于研发高性能、高可靠性的光谱成像相机,为科研院校提供更优的产品和服务。在《低空背景下无人机目标的光谱特征研究及目标检测应用》这篇论文中提到中达瑞和 LCTF 作为多…...

HTML前端开发:JavaScript 获取元素方法详解
作为前端开发者,高效获取 DOM 元素是必备技能。以下是 JS 中核心的获取元素方法,分为两大系列: 一、getElementBy... 系列 传统方法,直接通过 DOM 接口访问,返回动态集合(元素变化会实时更新)。…...
