向量数据库 | AI时代的航道灯塔
向量数据库 | AI时代的航道灯塔
- 什么是向量检索服务
- 拍照搜商品
- 你使用过向量数据库吗?使用体验?
- 为什么向量数据库能借由大模型引起众多关注
- 向量数据库在当前AI热潮中是昙花一现,还是未来AI时代的航道灯塔?
今天的话题主要是讨论向量数据库,在进入正文之前,先了解一下什么是向量检索服务,了解了向量检索服务,自然也就明白了什么是向量数据库。
什么是向量检索服务
节录一段官方关于向量检索服务的描述:【向量检索服务基于阿里云自研的向量引擎 Proxima 内核,提供具备水平拓展、全托管、云原生的高效向量检索服务。向量检索服务将强大的向量管理、查询等能力,通过简洁易用的 SDK/API 接口透出,方便在大模型知识库搭建、多模态 AI 搜索等多种应用场景上集成。】 向量检索服务产品首页:https://www.aliyun.com/product/ai/dashvector
其实,通过向量检索服务的定义还是不太容易理解什么是向量数据库,毕竟官方的定义往往比较专业,专业带来的结果就是晦涩难懂。那么我在这里基于一个大家在日常生活中经常会用到的场景来解释一下。
拍照搜商品
拍照搜商品用官方的话语描述就是【电商智能搜索和偏好推荐场景】,怎么理解呢?在日常生活中你走在大街上,当你看到某个东西觉得不错,比如衣服、鞋子、手办等等,那么你是否会拿出手机,点开购物APP的拍照搜商品呢?那么这个时候你用到的就是【电商智能搜索】,而当你搜索完一件商品之后,不管是通过图片还是文字搜索,购物APP都会在首页或者搜索栏下面为你推荐相似的商品,这就是【偏好推荐场景】。而你拍照搜商品或者文本搜商品,用到的数据库,就叫做【向量数据库】。到这里,你还会觉得向量数据库只是AI热潮中是昙花一现吗?
为了更好的理解什么是【电商智能搜索和偏好推荐场景】,这里我查阅了官方的描述,还是可以理解的,节录如下:【在电商智能搜索和偏好推荐场景中,向量数据库可以实现基于向量相似度的搜索和推荐功能。例如一个电商平台中包含了各种商品的图像和描述信息,用户在搜索商品时,可以通过图像或者描述信息查询相关的商品,并且还希望能够实现推荐功能,自动向用户推荐可能感兴趣的商品。
用户只需要先将商品的图像和描述信息使用Embedding技术转换为向量表示,并将其存储到向量数据库中。当用户输入查询请求时,向量检索服务可以将其转换为向量表示,然后计算查询向量与向量数据库中所有商品向量的相似度,然后返回相似度最高的几个商品向量。另外,还可以基于用户的历史行为和偏好通过向量检索服务将用户的历史浏览记录和购买记录转化为向量表示,并在向量数据库中查询与该向量最相似以及相似度较高的商品向量,为用户推荐可能感兴趣的商品,提供更加智能和个性化的服务、更加高效和优秀的性能与购买体验。】
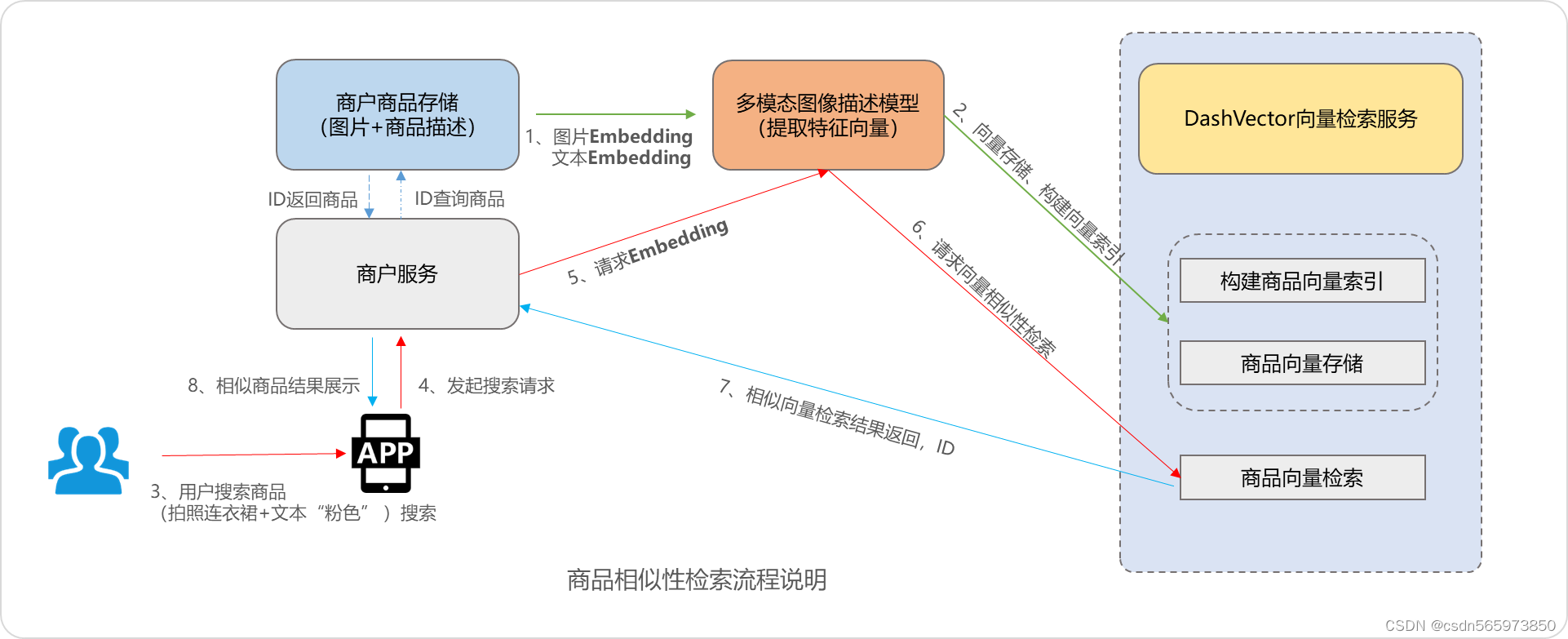
到这里,我想大家对于向量数据库,或者说对于向量检索服务,一定都会有一个比较明确的认知了吧,下面再来进入今天的话题讨论。
你使用过向量数据库吗?使用体验?
基于上面关于向量检索服务的介绍,我想大家应该都用过向量数据库了,只是你是在无意之间用过的。只要你有过网购,那么你都可以很认真的说:我用过向量数据库,并且体验还很不错。不管你是在淘宝、京东、抖音网购,不管你是以拍照搜商品还是文本搜商品,你用到的基本都是向量数据库。当然我不能保证全部都是,毕竟内部检索的核心技术我是无法知晓的。但是从用过的向量数据库的体验感来说,不管是拍照搜商品还是文本搜商品,体验感都很不错,数据返回很快,也都是自己有意向的商品。
为什么向量数据库能借由大模型引起众多关注
对于向量数据库来说,单独拿出来的向量数据库可以应用的场景有限,因而关注度不多。但是随着大模型深度学习的发展,大模型需要利用向量来表示复杂的数据,向量数据库能够高效存储和检索这些高维向量数据,为大模型提供强大的数据支撑。另外,向量数据库可以通过关联真实世界的数据点,如实体、关系等,构建知识图谱,进而支持模型查询和验证语义信息,从而降低模型输出错误的概率。在大模型中,需要处理的数据量极大,传统的关系型数据库几乎无法满足性能需求。而向量数据库由于其内部优化和并行处理能力,可以高效地处理大规模数据集,提供快速的查询和算法执行速度。
这也就是向量检索服务的另一个应用场景【自然语言处理等AI问答系统场景】,下面节录一段这个应用场景的官方描述:【问答系统是属于自然语言处理领域的常见现实应用。典型的问答系统比如通义千问、ChatGPT、在线客户服务系统、QA聊天机器人等。例如在一个问答系统,其中包含了一些预定义的问题和对应的答案。用户希望能够根据输入的问题,自动匹配到最相似的预定义问题,并返回对应的答案。为了实现此功能,首先可以通过向量检索服务将预定义的问题和答案转换为向量表示,并将其存储到向量数据库中。其次当用户输入问题时,向量检索服务可以将其转换为向量表示,并在向量数据库中查询与该向量最相似的问题向量。然后使用模型训练、问答推理、后期优化等步骤,实现类似通义千问、ChatGPT等的语言智能交互体系。】
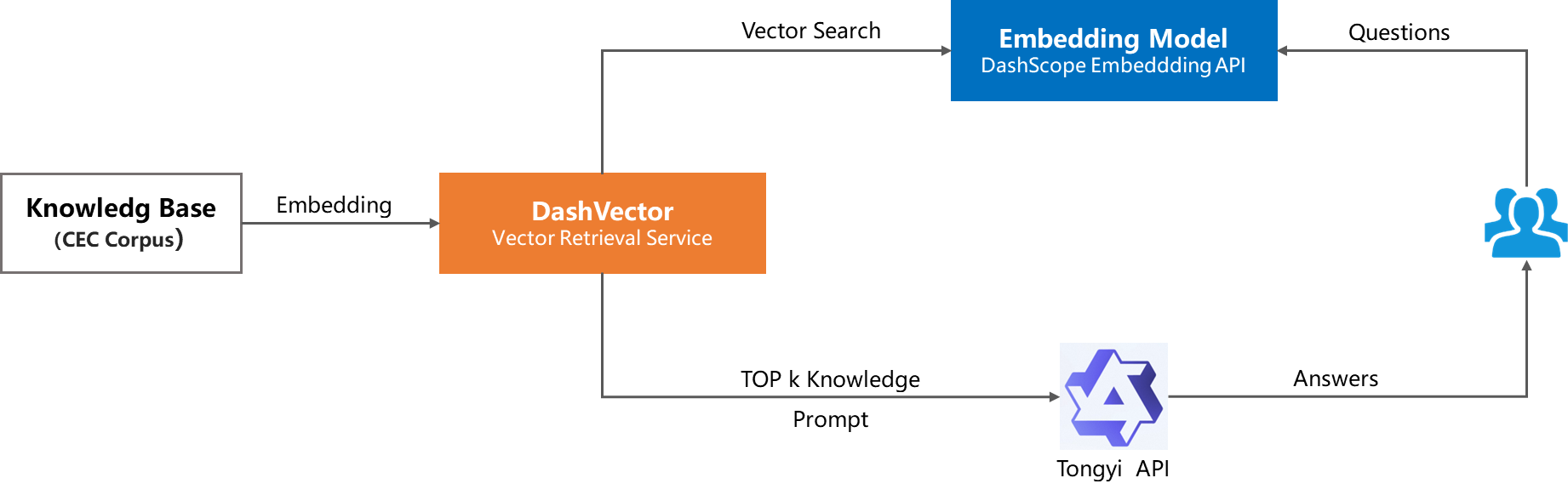
到这里,向量数据库为大模型提供了这么大的助力,那么向量数据库借由大模型引起众多关注也就顺理成章了。
向量数据库在当前AI热潮中是昙花一现,还是未来AI时代的航道灯塔?
眼下的AI热潮、大模型等,离不开向量数据库的助力,那么向量数据库可以说足以作为当前AI热潮的基石存在,那么基于此,向量数据库在当前AI热潮中自然也就不是昙花一现,而是AI时代的航道灯塔。

向量数据库在当下AI热潮中的作用,不管你说他是基石还是灯塔,向量数据库都担得起。未来的AI时代,数据体量只会更加庞大,在目前已知的数据库,也就只有向量数据库足以高效存储和检索这些高维向量数据,为AI提供强大的数据支撑,因此向量数据库必是未来AI时代的航道灯塔。
相关文章:

向量数据库 | AI时代的航道灯塔
向量数据库 | AI时代的航道灯塔 什么是向量检索服务拍照搜商品 你使用过向量数据库吗?使用体验?为什么向量数据库能借由大模型引起众多关注向量数据库在当前AI热潮中是昙花一现,还是未来AI时代的航道灯塔? 今天的话题主要是讨论向…...

Linux中的conntrack命令深入解析
在Linux网络管理和监控领域,conntrack命令是一个强大的工具,它提供了对netfilter连接跟踪系统的直接访问🔍。这篇文章将深入探讨conntrack的由来、底层原理、参数意义,以及其常见用法,并对返回结果的每个字段进行详细解…...
反截屏控制技术如何防止信息通过手机拍照泄漏?
反截屏控制技术为企业数据安全提供了重要的防护措施。通过以下几点,有效阻止了信息通过拍照等方式的泄漏: 反截屏控制开启,用户启动截屏操作时,允许非涉密内容截屏操作,但所有涉密内容窗口会自动隐藏,防止涉…...

0.k8s简介
目录 k8s是什么 k8s不是什么 云原生 微服务 整体式架构与微服务架构 微服务的特性 微服务的优势 k8s是什么 Kubernetes 是一个可移植、可扩展的开源平台,用于管理容器化的工作负载和服务,可促进声明式配置和自动化。 Kubernetes 拥有一个庞大且快…...
VScode 集成终端设置默认打开当前文件夹 mac系统
一.快捷键设置 搜索 openInIntegratedTerminal 如图: 二.设置cmd 默认打开位置 点击设置 搜索 ntegrated:cwd 如下图: 三.查看ip 快捷指令: ipconfig getifaddr en0...
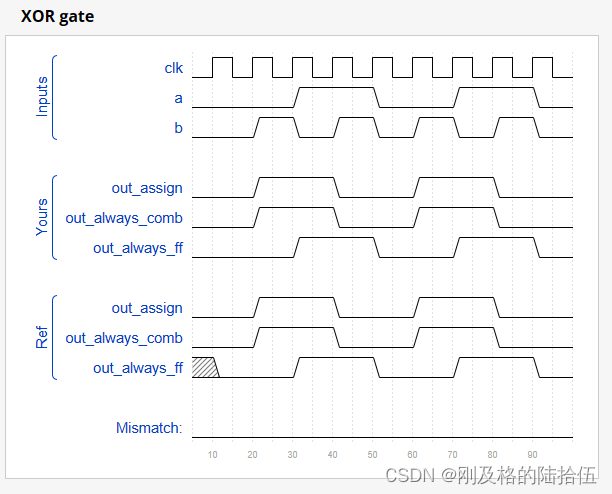
HDLbits 刷题 -- Alwaysblock2
学习: For hardware synthesis, there are two types of always blocks that are relevant: Combinational: always (*)Clocked: always (posedge clk) Clocked always blocks create a blob of combinational logic just like combinational always blocks, but…...
一、Docker部署GitLab(详细步骤)
Docker部署GitLab(详细步骤) 一、拉取镜像二、启动容器三、修改配置四、修改密码五、浏览器访问 一、拉取镜像 docker安装教程:https://qingsi.blog.csdn.net/article/details/131270071 docker pull gitlab/gitlab-ce:latest二、启动容器 …...
)
Vue3 Ajax(axios)
Vue 版本推荐使用 axios 来完成 ajax 请求。 安装方法 使用 cdn: <script src"https://unpkg.com/axios/dist/axios.min.js"></script> 使用 npm: $ npm install axios GET 方法 我们可以简单的读取 JSON 数据: const app {data() {r…...
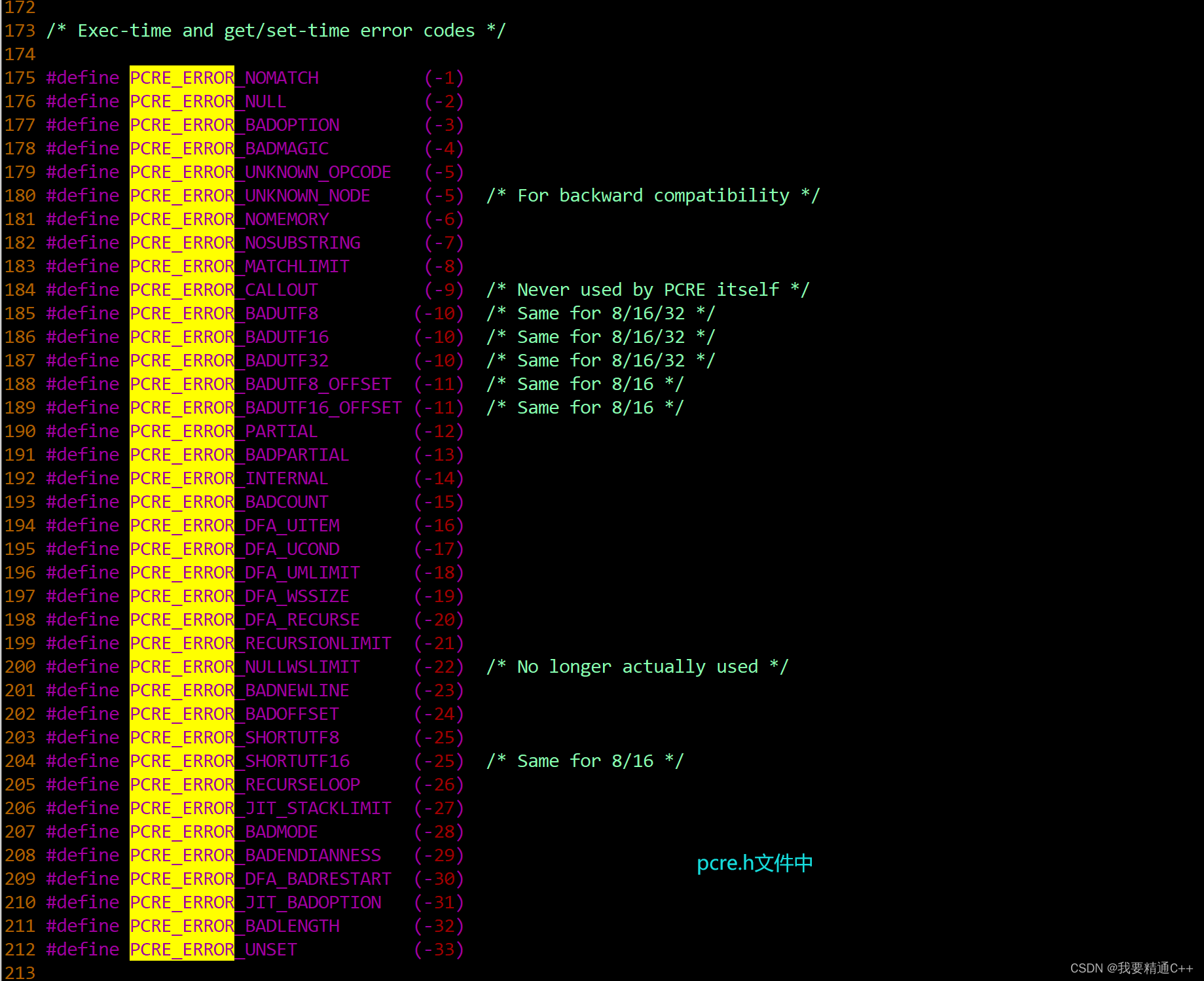
正则表达式引擎库汇合
1.总览表格 一些正则表达式库的对比 index库名编程语言说明代码示例编译指令1Posix正则C语言是C标准库中用于编译POSIX风格的正则表达式库 posix-re.cgcc posix-re.c 2PCRE库C语言提供类似Perl语言的一个正则表达式引擎库。 一般系统上对应/usr/lib64/libpcre.so这个库文件&am…...

eBay买家号注册下单容易死号?是什么原因导致?
随着电子商务的迅猛发展,跨境电商平台eBay日益成为众多消费者和商家的首选。然而,自去年下半年以来,eBay推出的新规则给买家号的注册带来了前所未有的挑战。许多新用户反映,在注册eBay买家号后,往往遭遇刚注册就被冻结…...
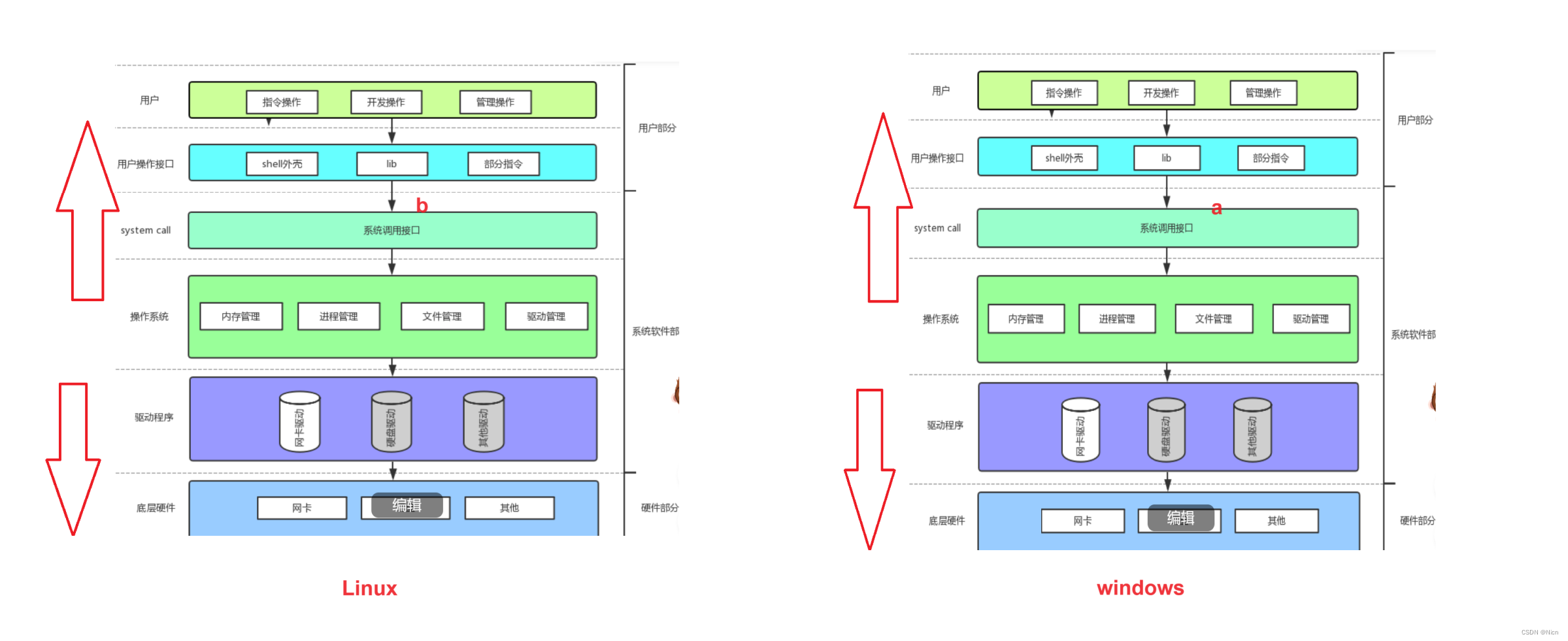
【Linux】-进程知识铺垫①计算机硬件的组织:冯诺依曼体系结构详细解读②关于操作系统对软硬件及用户的意义
目录 编辑 1.关于计算机的体系结构 1.1 冯诺依曼体系结构的诞生 2.冯诺依曼体系结构 2.1 cpu:运算器:更多的是让cpu具有特殊的数据计算功能: 2.2 控制器 2.3输入设备 2.4输出设备 3.计算机各个硬件设备之间的关系 4.内存与计算机效率 5.关于为什么总说…...

让ECC升级S/4HANA一步到位的“全面升级方案包”
SAP最新一代商务套件S/4HANA比ECC系统拥有更高性能的存储数据库HANA、更个性化的Fiori用户界面设计系统,能够大大提升系统效率,带来便捷、高效、良好的用户体验。但企业原先使用的ECC系统里面保存了积累多年的关键流程和数据,让企业面对系统升…...

AutoGluon
官网 amazon (base) PS C:\Users\gg葱> conda env list # conda environments: # pytorch1 C:\Users\gg葱\.conda\envs\pytorch1 base * D:\ANCDD:\Documents\LMm\env\pytorch2(base) PS C:\Users\gg葱> conda create --prefixD:/Doc…...
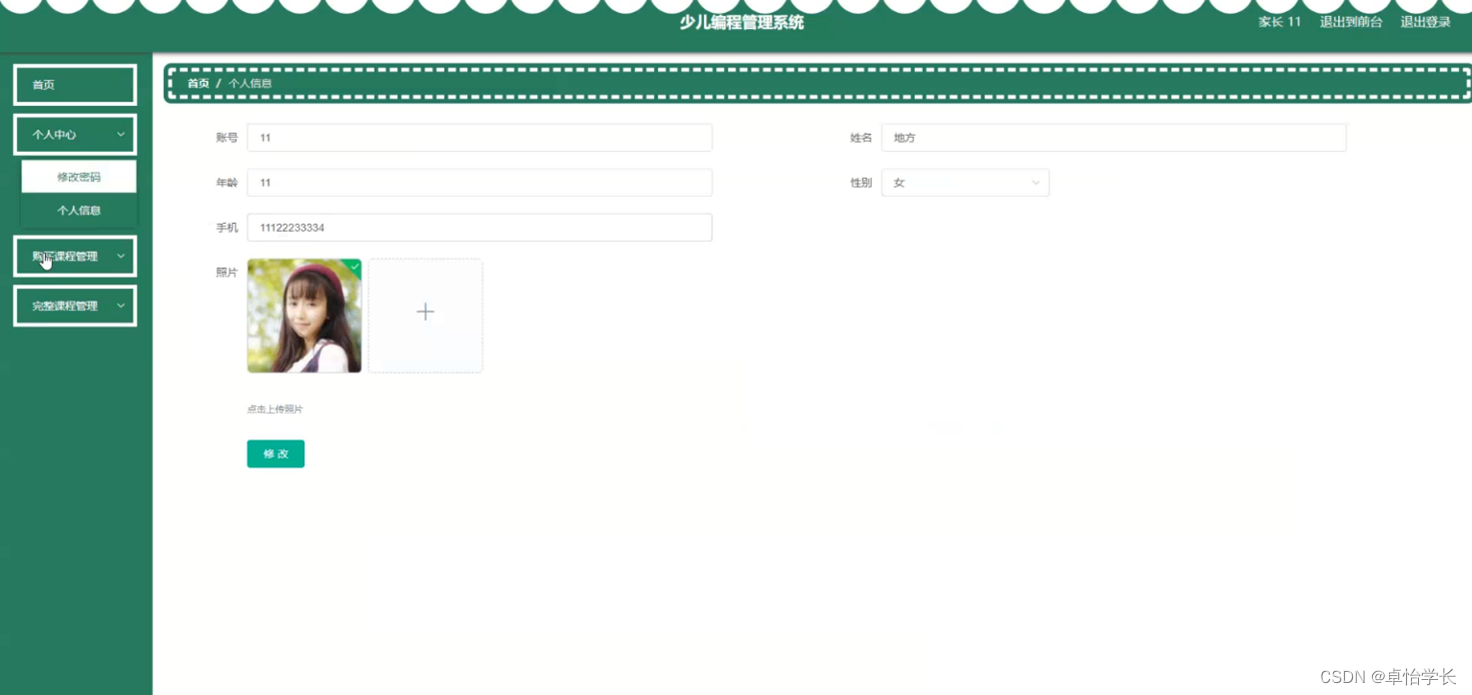
【网站项目】少儿编程管理系统
🙊作者简介:拥有多年开发工作经验,分享技术代码帮助学生学习,独立完成自己的项目或者毕业设计。 代码可以私聊博主获取。🌹赠送计算机毕业设计600个选题excel文件,帮助大学选题。赠送开题报告模板ÿ…...

基于C语言的数据结构--顺序表讲解及代码函数实现展示
本篇文章是数据结构的开篇,所以我们先来了解一下什么是数据结构。 什么是数据结构 数据结构是由“数据”和“结构”两个词组合而来,自然要以两个词分别去阐述。 首先,什么是数据?数据(data)是事实或观察的结果,是对客…...
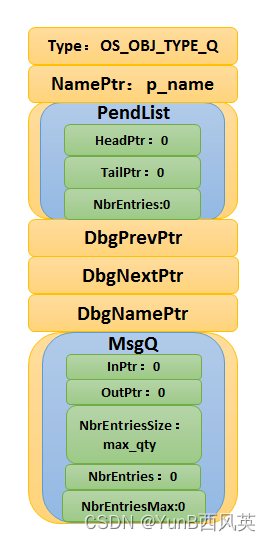
(学习日记)2024.03.31:UCOSIII第二十八节:消息队列常用函数
写在前面: 由于时间的不足与学习的碎片化,写博客变得有些奢侈。 但是对于记录学习(忘了以后能快速复习)的渴望一天天变得强烈。 既然如此 不如以天为单位,以时间为顺序,仅仅将博客当做一个知识学习的目录&a…...

DLC原理解析及其优化思考
1. 引言 Discreet Log Contract (DLC) 是由麻省理工学院的Tadge Dryja在2018年提出的一套基于预言机的合约执行方案。DLC 允许两方根据预定义的条件进行有条件付款。各方确定可能的结果并进行预签名,并在预言机签署结果时使用这些预签名来执行支付。 因此ÿ…...
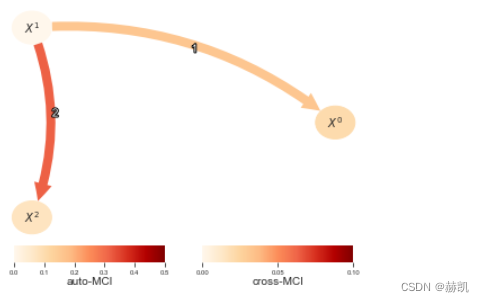
tigramite教程(七)使用TIGRAMITE 进行条件独立性测试
文章目录 概述1 连续数值变量1.1 ParCorr 偏相关(ParCorr类)1.2 鲁棒偏相关(RobustParCorr)非线性检验1.3 GPDC1.4 CMIknn 2a. 分类/符号时间序列2b. 混合分类/连续时间序列多变量X和Y的测试 概述 这个表格概述了 X ⊥ Y ∣ Z X\…...
设置)
【DevOps工具篇】使用Ansible部署Keycloak oauth2proxy 和 单点登录(SSO)设置
【DevOps工具篇】使用Ansible部署Keycloak oauth2proxy 和 单点登录(SSO)设置 目录 【DevOps工具篇】使用Ansible部署Keycloak oauth2proxy 和 单点登录(SSO)设置Ansible 基础知识部署 Keycloak创建 OIDC-客户端创建 oauth2proxy 部署顶级 Ansible PlaybookHost.iniplayboo…...

鸿蒙OS开发实例:【应用状态变量共享】
平时在开发的过程中,我们会在应用中共享数据,在不同的页面间共享信息。虽然常用的共享信息,也可以通过不同页面中组件间信息共享的方式,但有时使用应用级别的状态管理会让开发工作变得简单。 根据不同的使用场景,ArkT…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

多模态2025:技术路线“神仙打架”,视频生成冲上云霄
文|魏琳华 编|王一粟 一场大会,聚集了中国多模态大模型的“半壁江山”。 智源大会2025为期两天的论坛中,汇集了学界、创业公司和大厂等三方的热门选手,关于多模态的集中讨论达到了前所未有的热度。其中,…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

学校招生小程序源码介绍
基于ThinkPHPFastAdminUniApp开发的学校招生小程序源码,专为学校招生场景量身打造,功能实用且操作便捷。 从技术架构来看,ThinkPHP提供稳定可靠的后台服务,FastAdmin加速开发流程,UniApp则保障小程序在多端有良好的兼…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

【快手拥抱开源】通过快手团队开源的 KwaiCoder-AutoThink-preview 解锁大语言模型的潜力
引言: 在人工智能快速发展的浪潮中,快手Kwaipilot团队推出的 KwaiCoder-AutoThink-preview 具有里程碑意义——这是首个公开的AutoThink大语言模型(LLM)。该模型代表着该领域的重大突破,通过独特方式融合思考与非思考…...

对WWDC 2025 Keynote 内容的预测
借助我们以往对苹果公司发展路径的深入研究经验,以及大语言模型的分析能力,我们系统梳理了多年来苹果 WWDC 主题演讲的规律。在 WWDC 2025 即将揭幕之际,我们让 ChatGPT 对今年的 Keynote 内容进行了一个初步预测,聊作存档。等到明…...
:滤镜命令)
ffmpeg(四):滤镜命令
FFmpeg 的滤镜命令是用于音视频处理中的强大工具,可以完成剪裁、缩放、加水印、调色、合成、旋转、模糊、叠加字幕等复杂的操作。其核心语法格式一般如下: ffmpeg -i input.mp4 -vf "滤镜参数" output.mp4或者带音频滤镜: ffmpeg…...
