剑指Offer题目笔记27(动态规划单序列问题)
面试题89:

问题:
输入一个数组表示某条街道上的一排房屋内财产的数量。相邻两栋房屋不能同时被盗,问小偷能偷取到的最多财物。
解决方案一(带缓存的递归):
解决方案:
- 由于有报警系统,小偷不能同时偷相邻两栋房屋,故小偷在到达标号为i的房屋时他能偷取的财物的最大值,即f(i)=max(f(i-2)+nums[i],f(i-1))。
- 创建一个数组dp,它的第i个元素dp[i]用来保存f(i)的结果。如果f(i)之前已经计算出结果,那么只需要从数组dp中读取dp[i]的值,不用再重复计算。如果之前从来没有计算过,则根据状态转移方程递归计算。
源代码:
class Solution {public int rob(int[] nums) {int[] dp = new int[nums.length];//将dp数组的所有值赋值为-1Arrays.fill(dp,-1);dfs(nums,nums.length-1,dp);return dp[nums.length-1];}private void dfs(int[] nums,int len,int[] dp){if(len == 0){dp[len] = nums[0];}else if(len == 1){dp[len] = Math.max(nums[0],nums[1]);}else if(dp[len] < 0){dfs(nums,len-1,dp);dfs(nums,len-2,dp);dp[len] = Math.max(dp[len-1],dp[len-2] + nums[len]);}}
}
解决方案二:(空间复杂度为O(n)的迭代):
解决方案:
由下到上,先求出f(0)和f(1)的值,再通过状态转移方程f(i) = Math,max(f(i-1),f(i-2) + nums[i])求出f(2)以此类推求得f(i)。
源代码:
class Solution {public int rob(int[] nums) {int len = nums.length;int[] dp = new int[len];dp[0] = nums[0];if(len >= 2){dp[1] = Math.max(nums[1],nums[0]);}for(int i = 2;i < len;i++){dp[i] = Math.max(dp[i-1],dp[i-2] + nums[i]);}return dp[len-1];}
}
解决方案三:(空间复杂度为O(1)的迭代):
解决方案:
观察上述代码,就能发现计算“dp[i]”时只需要用到“dp[i-1]”和“dp[i-2]”这两个值,也就是说,只需要缓存两个值就足够了,并不需要一个长度为n的数组。
源代码:
class Solution {public int rob(int[] nums) {int len = nums.length;int[] dp = new int[2];dp[0] = nums[0];if(len >= 2){dp[1] = Math.max(nums[0],nums[1]);}for(int i = 2;i < len;i++){dp[i % 2] = Math.max(dp[(i-1) % 2],dp[(i-2) % 2 ] + nums[i]);}return dp[(len - 1) % 2];}
}
解决方案四:(使用两个状态转移方程):
解决方案:
由于小偷到达标记为i的房屋是有两个选择,他进去偷东西和不进去偷东西,定义f(i)为不进去偷东西,g(i)为进去偷东西,因此f(i)= max(f(i-1),g(i-1)),g(i) = f(i-1) + nums[1]。这两个状态转移方程有隐含条件i必须大于0,不然i-1没有意义,因此f(0)= 0,g(0) = nums[0]。
源代码:
class Solution {public int rob(int[] nums) {int len = nums.length;int[][] dp = new int[2][2];//dp【0】为f(i)dp[0][0] = 0;//dp【1】为g(i)dp[1][0] = nums[0];for(int i = 1;i < len;i++){dp[0][i % 2] = Math.max(dp[0][(i - 1) % 2],dp[1][(i - 1) % 2]);dp[1][i % 2] = Math.max(dp[0][i % 2],dp[0][(i-1) % 2] + nums[i]);}return Math.max(dp[0][(len - 1) % 2],dp[1][(len - 1) % 2]);}
}
面试题90:

问题:
一条环形街道上有若干房屋,输入一个数组表示该条街道上的房屋内财产的数量,计算小偷在这条街道上最多能偷取到的财产数量。
解决方案:
- 如果小偷去偷标号为0的房屋,那么他就不能去偷标号为n-1的房屋;如果小偷去偷标号为n-1的房屋,那么他就不能去标号为0的房屋。
- 可以将这个问题分解成两个子问题:一个问题是求小偷从标号为0开始到标号为n-2结束的房屋内能偷得的最多财物数量,另一个问题是求小偷从标号为1开始到标号为n-1结束的房屋内能偷得的最多财物数量。
源代码:
class Solution {public int rob(int[] nums) {int len = nums.length;if(len == 0){return 0;}if(len == 1){return nums[0];}//0~n-2int result1 = dfs(nums,0,len-2);//1~n-1int result2 = dfs(nums,1,len-1);return Math.max(result1,result2);}private int dfs(int[] nums,int start,int end){int[] dp = new int[2];dp[0] = nums[start];if(start < end){dp[1] = Math.max(nums[start],nums[start+1]);}for(int i = start+2;i <= end;i++){int j = i - start;dp[j % 2] = Math.max(dp[(j-1) % 2],dp[(j-2) % 2] + nums[i]); }return Math.max(dp[0],dp[1]);}
}
面试题91:

问题:
一排n幢房子要粉刷成红色、绿色和蓝色,不同房子被粉刷成不同颜色的成本不同。要求任意相邻的两幢房子的颜色都不一样。
解决方案:
- 当计算粉刷标记为i的房子时的成本,得先考虑标记i-1的房子的颜色。因此,需要3个表达式,r(i)表示粉刷红色、g(i)表示粉刷绿色、b(i)表示粉刷蓝色。
- 如果标记i的房子粉刷红色时,那么标记i-1的房子可以被粉刷为绿色或蓝色,r(i) = min(g(i-1),b(i-1))+ costs[i]。如果标记i的房子粉刷绿色时,那么标记i-1的房子可以被粉刷为红色或蓝色,g(i) = min(r(i-1),b(i-1))+ costs[i]。如果标记i的房子粉刷蓝色时,那么标记i-1的房子可以被粉刷为绿色或红色,b(i) = min(g(i-1),r(i-1))+ costs[i]。
源代码:
class Solution {public int minCost(int[][] costs) {int len = costs.length;//将三个一维数组合成为一个二维数组int[][] dp = new int[3][2];for(int i = 0;i < 3;i++){dp[i][0] = costs[0][i];}for(int i = 1;i < len;i++){for(int j = 0;j < 3;j++){//计算另外两种颜色的成本int result1 = dp[(j + 1) % 3][(i - 1) % 2];int result2 = dp[(j + 2) % 3][(i - 1) % 2];dp[j][i % 2] = Math.min(result1,result2) + costs[i][j];}}int last = (len-1) % 2;return Math.min(Math.min(dp[0][last],dp[1][last]),dp[2][last]);}
}
面试题92:

问题:
输入一个只包含‘0’和‘1’的字符串,至少需要翻转几个字符,才可以使翻转之后的字符串中所有的‘0’位于‘1’的前面。
解决方案:
- 由于翻转下标为i的字符依赖于前i个字符翻转之后的最后一个字符是‘0’还是‘1’,因此要分两种情况讨论,假设f(i)是翻转之后最后一个字符为0的函数,g(i)为翻转之后最后一个字符为1的函数。
- 如果下标为i的字符是‘0’,那么f(i)= f(i-1)不需要进行翻转;如果下标为i的字符是‘1’,那么f(i) = f(i-1)+ 1。如果下标为i的字符是‘0’,那么g(i) = min(f(i-1),g(i-1))+ 1,因为当我们将下标为i的字符翻转为‘1’时,那么不管下标i-1的字符是0或1都可以;如果下标为i的字符是‘1’,那么g(i)= min(f(i-1),g(i-1)),因为下标为i的字符已经为‘1’了,不需要翻转。
源代码:
class Solution {public int minFlipsMonoIncr(String s) {int len = s.length();int[][] dp = new int[2][2];char ch = s.charAt(0);dp[0][0] = ch == '0'?0:1;dp[1][0] = ch == '0'?1:0;for(int i = 1;i < len;i++){char sh = s.charAt(i);int result1 = dp[0][(i - 1) % 2];int result2 = dp[1][(i - 1) % 2];dp[0][i % 2] = result1 + (sh == '0'?0:1);dp[1][i % 2] = Math.min(result1,result2) + (sh == '1'?0:1); }return Math.min(dp[0][(len - 1) % 2],dp[1][(len - 1) % 2]);}
}
面试题93:

问题:
输入一个没有重复数字的单调递增的数组,数组中至少有3个数字,请问数组中最长的斐波那契数列的长度是多少。
解决方案:
- 将数组记为A,A[i]表示数组中下标为i的数字。对于每个j(0≤j<i),A[j]都有可能是在某个斐波那契数列中A[i]前面的一个数字。如果存在一个k(0≤k< j)满足A[k]+A[j]=A[i],那么这3个数字就组成了一个斐波那契数列。这个以A[i]为结尾、前一个数字是A[j]的斐波那契数列是在以A[j]为结尾、前一个数字是A[k]的序列的基础上增加一个数字A[i],因此前者的长度是在后者的长度的基础上加1。
- 由于状态转移方程有两个参数i和j,因此需要一个二维数组来缓存f(i,j)的计算结果。i对应二维数组的行号,j对应二维数组的列号。由于i大于j,因此实际上只用到了二维数组的左下角部分。如果数组的长度是n,那么i的取值范围为1~n-1,而j的取值范围为0~n-2。
源代码:
class Solution {public int lenLongestFibSubseq(int[] arr) {int len = arr.length;//使用map数组记录每个数字在数组中的下标Map<Integer,Integer> map = new HashMap<>();for(int i = 0;i < len;i++){map.put(arr[i],i);}int[][] dp = new int[len][len];int result = 2;for(int i = 1;i < len;i++){for(int j = 0;j < i;j++){//判断数组中是否存在一个数字 arr[k]满足arr[k]=arr[i]-arr[j]。int k = map.getOrDefault(arr[i]-arr[j],-1);//如果存在,就在f(j,k)的基础上加一dp[i][j] = k >= 0 && k < j?dp[j][k] + 1:2;result = Math.max(result,dp[i][j]);}}return result > 2?result:0;}
}
面试题94:

问题:
输入一个字符串,请问至少需要分割几次才可以使分割出的每个字符串都是回文。
解决方案:
- 假设字符串为S,下标为i的字符为S[i],下标从j到i的子字符串为S[j…i]。用 f(i)表示从下标为0到i的子字符串S[0…i]的符合条件的最少分割次数。如果字符串的长度是n,那么f(n-1)就是问题的解。
- 如果子字符串S[0…i]本身就是一个回文,那么不需要分割就符合要求,此时f(i)等于0。如果子字符串S[0…i]不是一个回文,那么对每个下标j(1≤j≤i)逐一判断子字符串S[j…i]是不是回文。如果是回文,那么这就是一个有效的分割方法,此时的分割次数相当于子字符串S[0…j-1]的分割次数再加1,因为这是将子字符串S[0…j-1]按照要求分割之后再在S[j-1]和S[j]这两个字符中间再分割一次。因此,f(i)就是所有符合条件的j对应的f(j-1)的最小值加1。
源代码:
class Solution {public int minCut(String s) {int len = s.length();//使用二维数组记录j到i是否回文boolean[][] flag = new boolean[len][len];for(int i = 0;i < len;i++){for(int j = 0;j <= i;j++){char ch1 = s.charAt(i);char ch2 = s.charAt(j);//i <= j+1用于判断i和j相邻的情况、flag[j+1][i-1]用于判断j到i不相邻的情况if(ch1 == ch2 && (i <= j+1 || flag[j+1][i-1])){flag[j][i] = true;}}}int[] dp = new int[len];for(int i = 0;i < len;i++){//如果0到i是回文数,那么就不需要分割if(flag[0][i]){dp[i] = 0;}else{//先做最坏的打算,字符需要分割成一个一个的字符。例如abcd,就需要分割3次dp[i] = i;for(int j = 1;j <= i;j++){//如果j到i是回文数,那么就在dp【j-1】切割次数的基础上加一if(flag[j][i]){dp[i] = Math.min(dp[i],dp[j-1] + 1);}}}}return dp[len-1];}
}
相关文章:

剑指Offer题目笔记27(动态规划单序列问题)
面试题89: 问题: 输入一个数组表示某条街道上的一排房屋内财产的数量。相邻两栋房屋不能同时被盗,问小偷能偷取到的最多财物。 解决方案一(带缓存的递归): 解决方案: 由于有报警系统&…...

撸代码时,有哪些习惯一定要坚持?
我从2011年开始做单片机开发,一直保持以下撸代码的习惯。 1.做好代码版本管理 有些人,喜欢一个程序干到底,直到实现全部的产品功能,我以前做51单片机的项目就是这样。 如果功能比较多的产品,我不建议这样做࿰…...
)
【leetcode面试经典150题】17.罗马数字转整数(C++)
【leetcode面试经典150题】专栏系列将为准备暑期实习生以及秋招的同学们提高在面试时的经典面试算法题的思路和想法。本专栏将以一题多解和精简算法思路为主,题解使用C语言。(若有使用其他语言的同学也可了解题解思路,本质上语法内容一致&…...
前后端开发之——文章分类管理
原文地址:前后端开发之——文章分类管理 - Pleasure的博客 下面是正文内容: 前言 上回书说到 文章管理系统之添加文章分类。就是通过点击“新建文章分类”按钮从而在服务端数据库中增加一个文章分类。 对于文章分类这个对象,增删改查属于配…...
第12届蓝桥杯省赛 ---- C/C++ C组
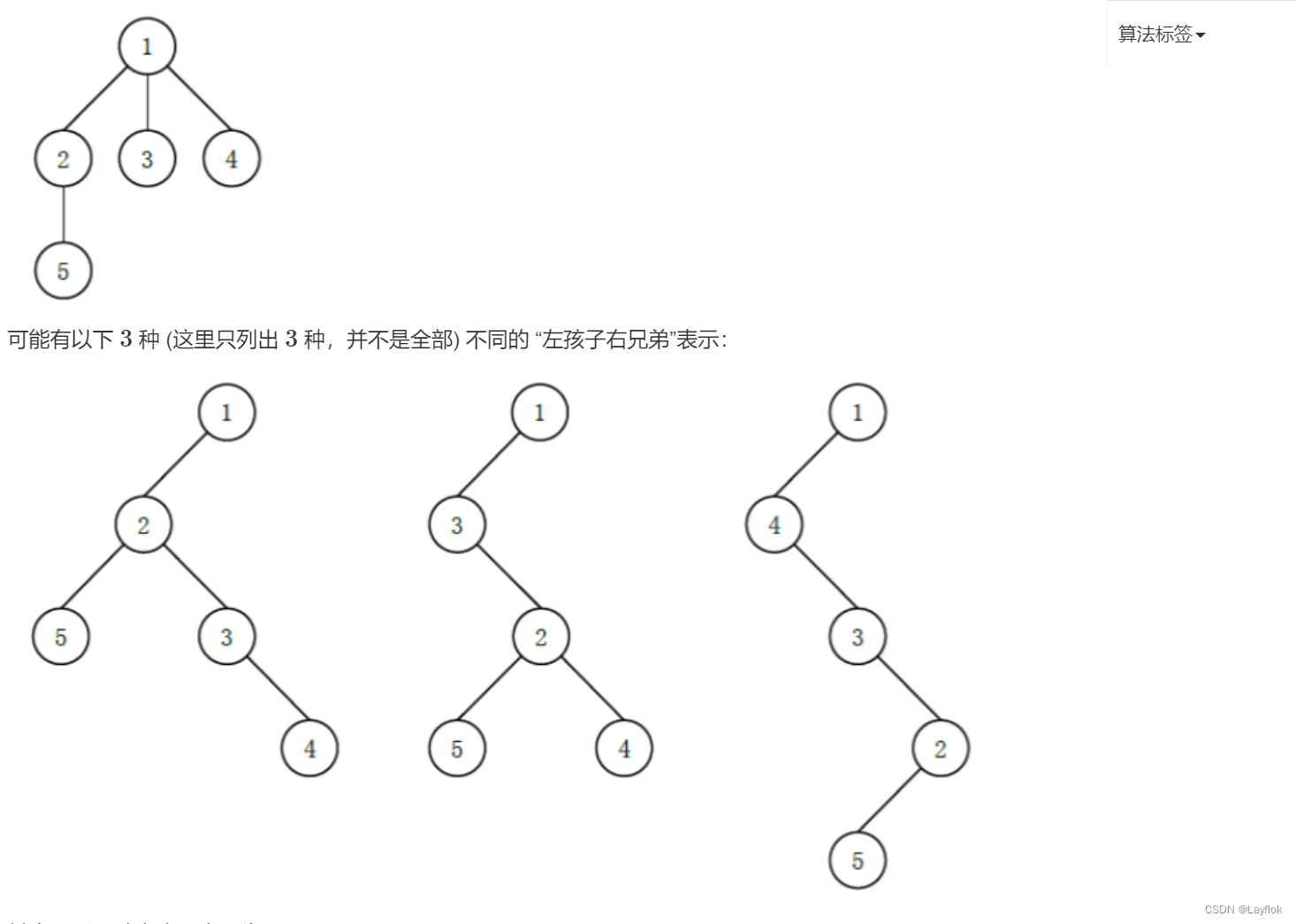
文章目录 1. ASC2. 空间3. 卡片4. 相乘5. 路径6.时间显示7.最少砝码8. 杨辉三角形9. 左孩子右兄弟 第12届蓝桥杯省赛,C/C C组真题,第10题不是很清楚,题解不敢乱放😁😁😁 1. ASC 额。。。。 #include <i…...
IVS模型解释
核心思路 【Implied volatility surface predictability: The case of commodity markets】 半参数化模型:利用各种参数(或者因子)对隐含波动率进行降维(静态参数化因子模型),对参数化因子的时间序列进行间接的建模 基于非对称…...

通用开发技能系列:Git
云原生学习路线导航页(持续更新中) 本文是 通用开发技能系列 文章,主要对编程通用技能Git进行学习 1.为什么使用版本控制系统 版本控制系统可以解决的问题 代码备份很重要版本控制很重要协同工作很重要责任追溯很重要 常见的版本控制系统 Gi…...
最新怎么订阅OnlyFans上喜欢的博主,详细教程
大家好,本文教大家如何用虚拟信用卡在 Onlyfans 订阅,链接在浏览器打开地址https://bewildcard.com/i/GPT310,虚拟卡开好之后,用支付宝充值就可以进行订阅OnlyFans平台的博主了。 什么是OnlyFans? OnlyFans 是一个提…...
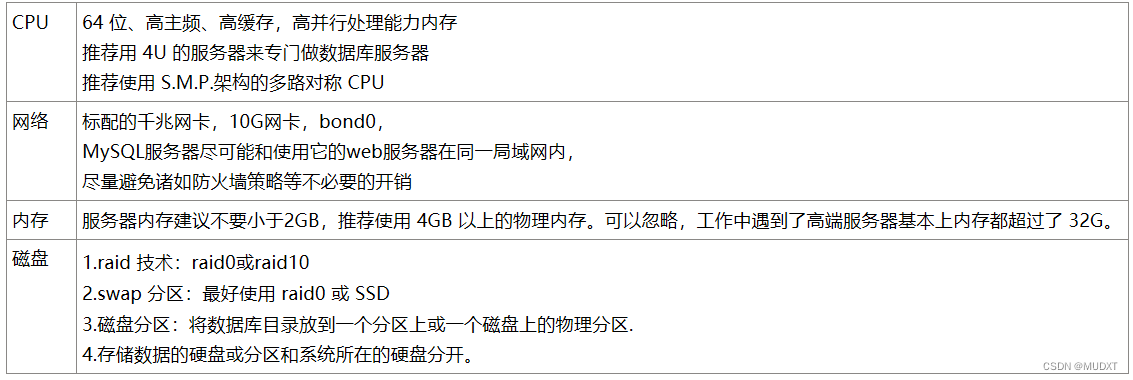
Mysql故障和优化
一、MySQL故障 二、MySQL优化 1.硬件优化: 2.数据库设计与规划 1.提前估计数据量,使用什么存储引擎 2.数据库服务器专机专用,避免额外的服务可能导致的性能下降和不稳定性 3.增加多台服务器,以达到稳定、高效的效果。主从同步、…...
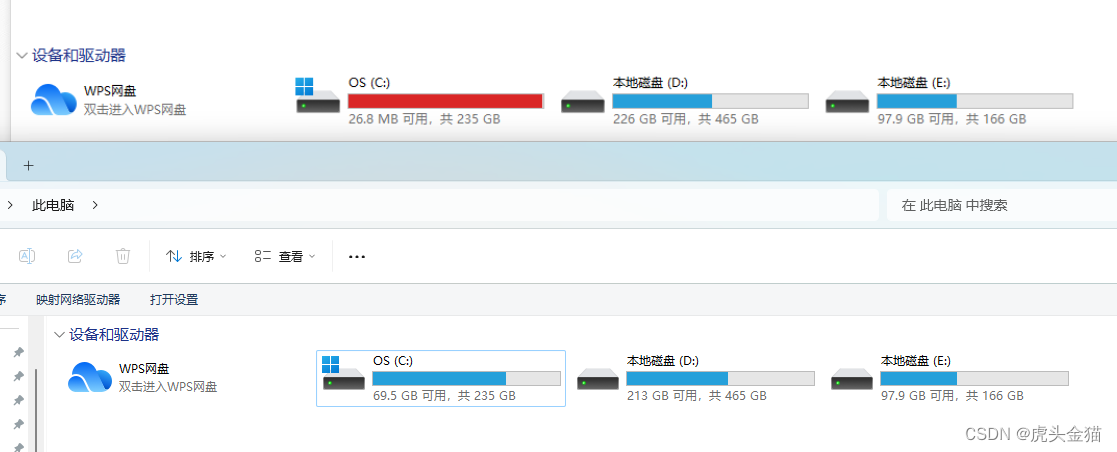
Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理
Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理 文章目录 Windows系统C盘空间优化进阶:磁盘清理与Docker日志管理磁盘清理工具 使用“运行”命令访问磁盘清理利用存储感知自动管理空间清理WinSxS文件夹结合手动清理策略 小结删除临时文件总结&…...

14届蓝桥杯 C/C++ B组 T7 子串简写 (字符串)
采用存储目标字符下标的方法,此题的想法比较新奇,故予以记录。 存好下标之后,可以先定位好启始的字符,然后去搜结尾字符符合长度k并且最靠近启始字符的下标,找到之后可以直接取到这个下标之后的所有下标,因…...
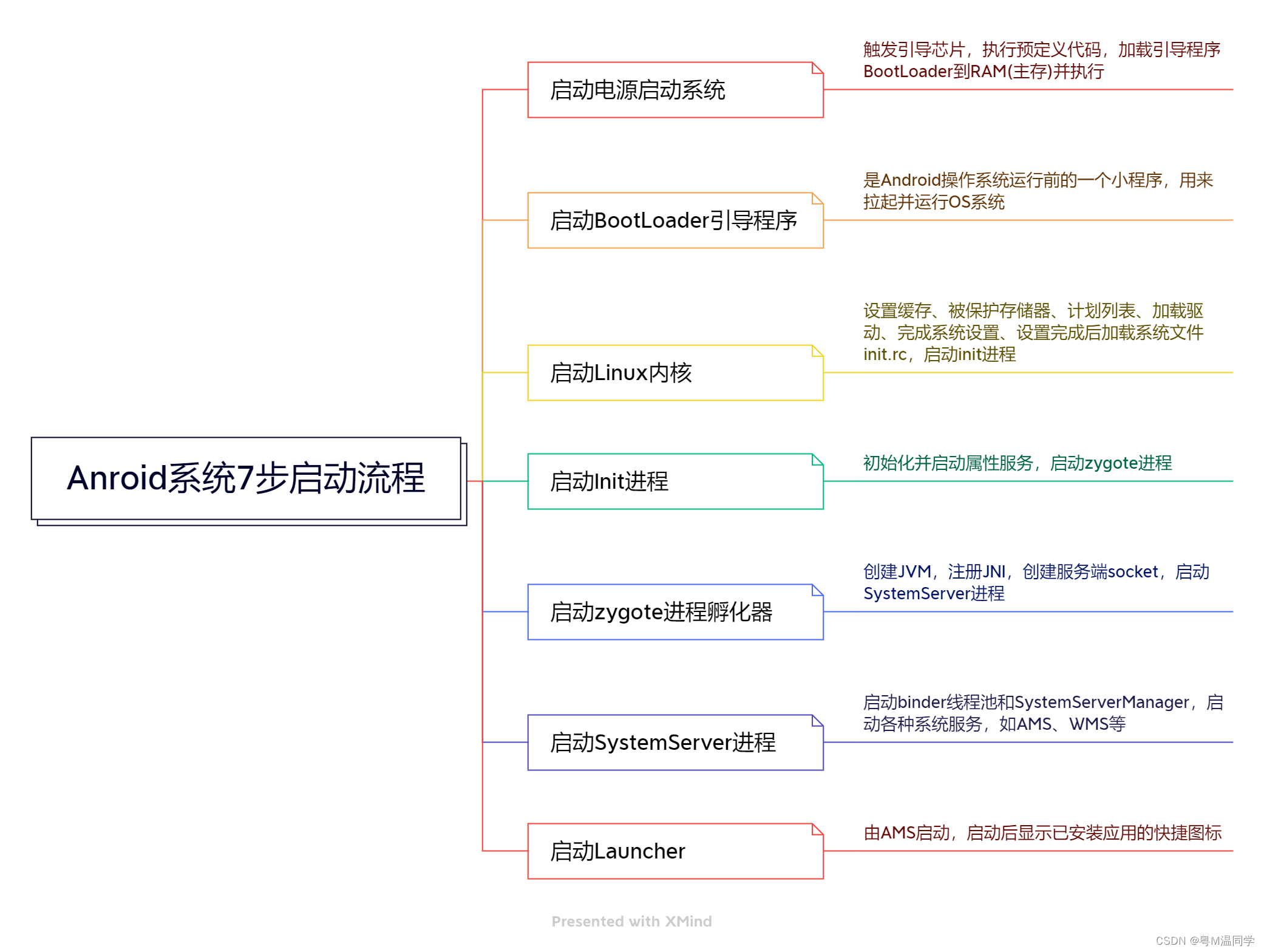
Android 系统大致启动流程
Android启动流程大体为:BootRom -> BootLoader -> Kernel -> Init -> Zygote -> SystemServer ->Launcher 1、Loader层 1.1、Boot ROM 电源按下,引导芯片代码开始从预定义的地方(固化在ROM)开始执行࿰…...
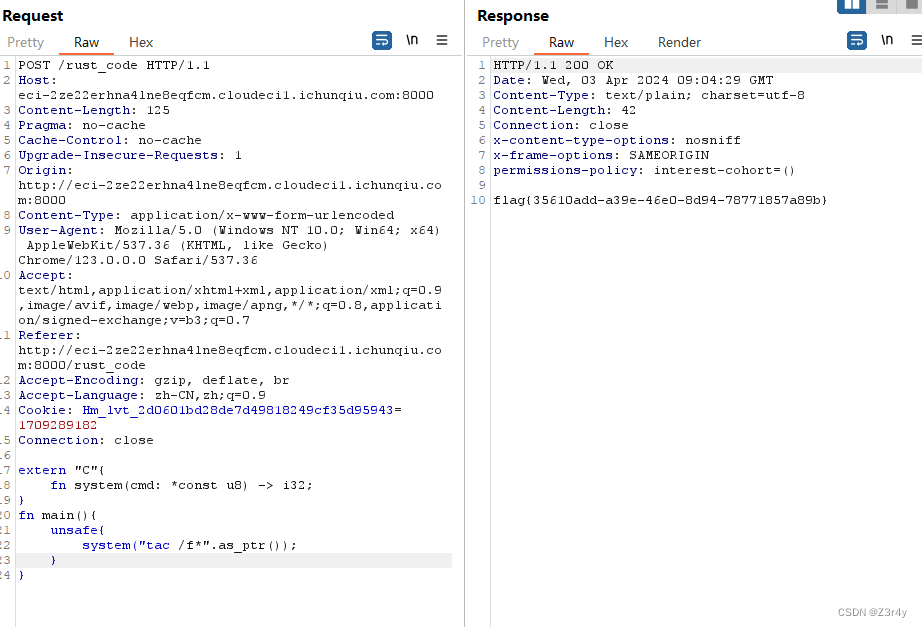
【Web】2024红明谷CTF初赛个人wp(2/4)
目录 ezphp playground 时间原因只打了2个小时,出了2道,简单记录一下 ezphp 参考文章 PHP filter chains: file read from error-based oracle https://github.com/synacktiv/php_filter_chains_oracle_exploit 用上面的脚本爆出部分源码ÿ…...
stable-diffusion-webui安装教程
现在AI开始进入绘画领域,并且能自动根据文本来创建图片出来,这是一个划时代的进步。 这时候,我也不能落后,要紧跟上时代的步伐,那么也来学习一下stable-diffusion的使用,这样也算多一项对技术的认识,提高对AI的认知。 从网上看到很多stable-diffusion-webui的安装,其…...

如何魔改 diffusers 中的 pipelines
如何魔改 diffusers 中的 pipelines 整个 Stable Diffusion 及其 pipeline 长得就很适合 hack 的样子。不管是通过简单地调整采样过程中的一些参数,还是直接魔改 pipeline 内部甚至 UNet 内部的 Attention,都可以实现很多有趣的功能或采样生图结果。 本…...

解放办公室的利器!让证卡打印机轻松应对繁忙工作场景
在现代办公室中,证卡打印机已经成为不可或缺的工作利器。但是,在繁忙的工作场景中,我们经常忽视了它的保养和清洁。然而,正确的清洁和维护不仅可以延长打印机的寿命,还可以提高工作效率,确保每一次打印都是…...

2012年认证杯SPSSPRO杯数学建模A题(第二阶段)蜘蛛网全过程文档及程序
2012年认证杯SPSSPRO杯数学建模 A题 蜘蛛网 原题再现: 第二阶段问题 现在我们假设一个具体的环境。假设有一个凸多边形的区域,蜘蛛准备在这个区域(或其一部分)上结一张网。 问题一: 在区域的边界上安置有若干…...
ES学习日记(七)-------Kibana安装和简易使用
前言 首先明确一点,Kibana是一个软件,不是插件。 Kibana 是一款开源的数据分析和可视化平台,它是 Elastic stack 成员之一,设计用于和Elasticsearch 协作。您可以使用 Kibana 对 Elasticsearch 索引中的数据进行搜索,…...

react 父子组件的渲染机制 | 优化手段
文章目录 父子组件的渲染机制优化手段与实践写法父组件:下发stateprops.children 传递无状态组件props传递组件 React.memo缓存子组件与useCallback结合 父子组件的渲染机制 渲染分初次渲染和重新渲染 React组件会在两种情况下发生重新渲染 当组件自身的state发生…...

elementPlus el-table动态列扩展及二维表格
1、循环列数据源,动态生成列 <template><div><el-table ref"table" :data"pageData.tableData" stripe style"width: 100%"><el-table-column v-for"column in pageData.columns" :key"column.p…...

在HarmonyOS ArkTS ArkUI-X 5.0及以上版本中,手势开发全攻略:
在 HarmonyOS 应用开发中,手势交互是连接用户与设备的核心纽带。ArkTS 框架提供了丰富的手势处理能力,既支持点击、长按、拖拽等基础单一手势的精细控制,也能通过多种绑定策略解决父子组件的手势竞争问题。本文将结合官方开发文档,…...

django filter 统计数量 按属性去重
在Django中,如果你想要根据某个属性对查询集进行去重并统计数量,你可以使用values()方法配合annotate()方法来实现。这里有两种常见的方法来完成这个需求: 方法1:使用annotate()和Count 假设你有一个模型Item,并且你想…...

如何在看板中有效管理突发紧急任务
在看板中有效管理突发紧急任务需要:设立专门的紧急任务通道、重新调整任务优先级、保持适度的WIP(Work-in-Progress)弹性、优化任务处理流程、提高团队应对突发情况的敏捷性。其中,设立专门的紧急任务通道尤为重要,这能…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

vue3 daterange正则踩坑
<el-form-item label"空置时间" prop"vacantTime"> <el-date-picker v-model"form.vacantTime" type"daterange" start-placeholder"开始日期" end-placeholder"结束日期" clearable :editable"fal…...

热门Chrome扩展程序存在明文传输风险,用户隐私安全受威胁
赛门铁克威胁猎手团队最新报告披露,数款拥有数百万活跃用户的Chrome扩展程序正在通过未加密的HTTP连接静默泄露用户敏感数据,严重威胁用户隐私安全。 知名扩展程序存在明文传输风险 尽管宣称提供安全浏览、数据分析或便捷界面等功能,但SEMR…...

二维FDTD算法仿真
二维FDTD算法仿真,并带完全匹配层,输入波形为高斯波、平面波 FDTD_二维/FDTD.zip , 6075 FDTD_二维/FDTD_31.m , 1029 FDTD_二维/FDTD_32.m , 2806 FDTD_二维/FDTD_33.m , 3782 FDTD_二维/FDTD_34.m , 4182 FDTD_二维/FDTD_35.m , 4793...

yaml读取写入常见错误 (‘cannot represent an object‘, 117)
错误一:yaml.representer.RepresenterError: (‘cannot represent an object’, 117) 出现这个问题一直没找到原因,后面把yaml.safe_dump直接替换成yaml.dump,确实能保存,但出现乱码: 放弃yaml.dump,又切…...
