探索数据结构:特殊的双向队列
✨✨ 欢迎大家来到贝蒂大讲堂✨✨
🎈🎈养成好习惯,先赞后看哦~🎈🎈
所属专栏:数据结构与算法
贝蒂的主页:Betty’s blog
1. 双向队列的定义
**双向队列(double‑ended queue)**是一种特殊的队列,它允许在队列的队尾与队头插入与删除元素。根据其定义,我们也可以理解为两个栈在栈底相连。
- 队尾入队

- 队首入队
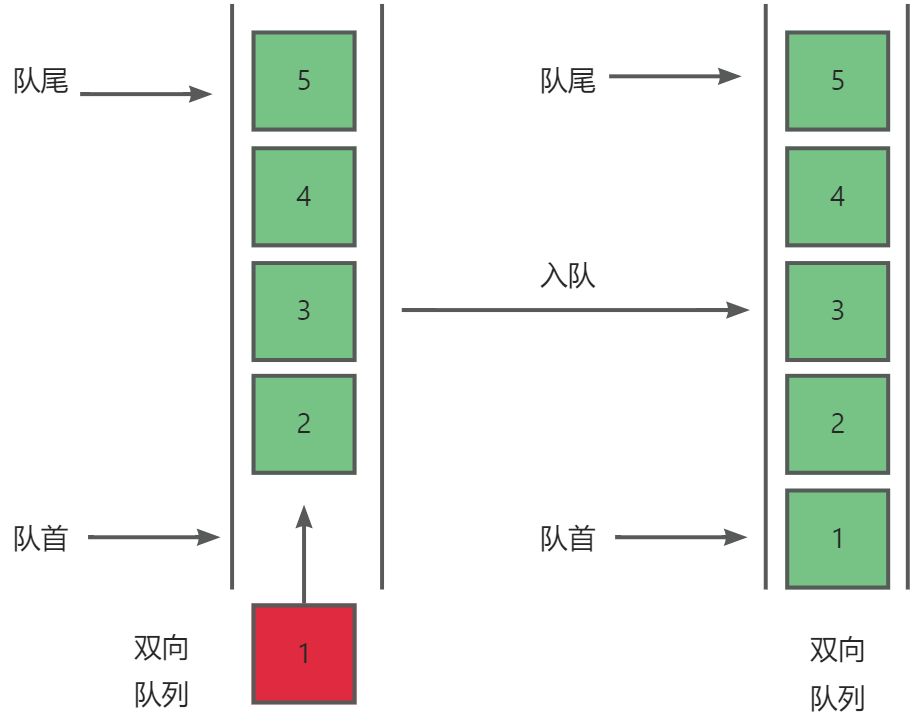
- 队尾出队
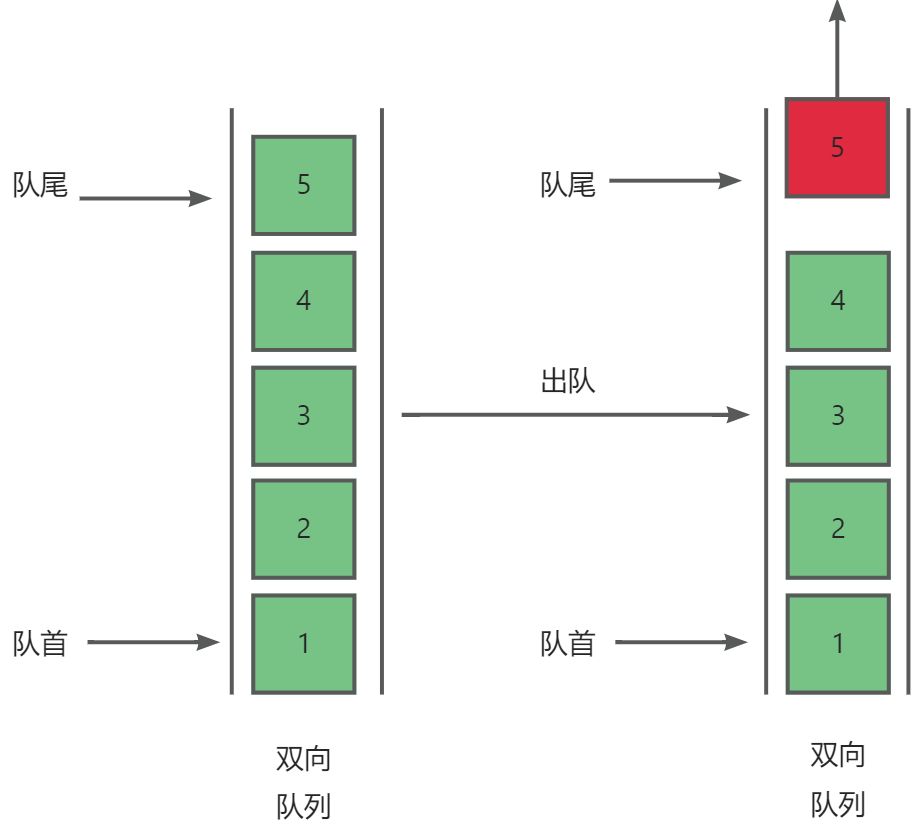
- 队尾出队

2. 双向队列的分类
双向队列也是线性表的一种,所以也可以分别用链表与数组实现。基于链表实现:为了方便双向队列在尾部的插入与删除操作,所以我们选用双向链表。基于数组实现:与队列实现类似,需要用循环数组(原因参考队列实现)。
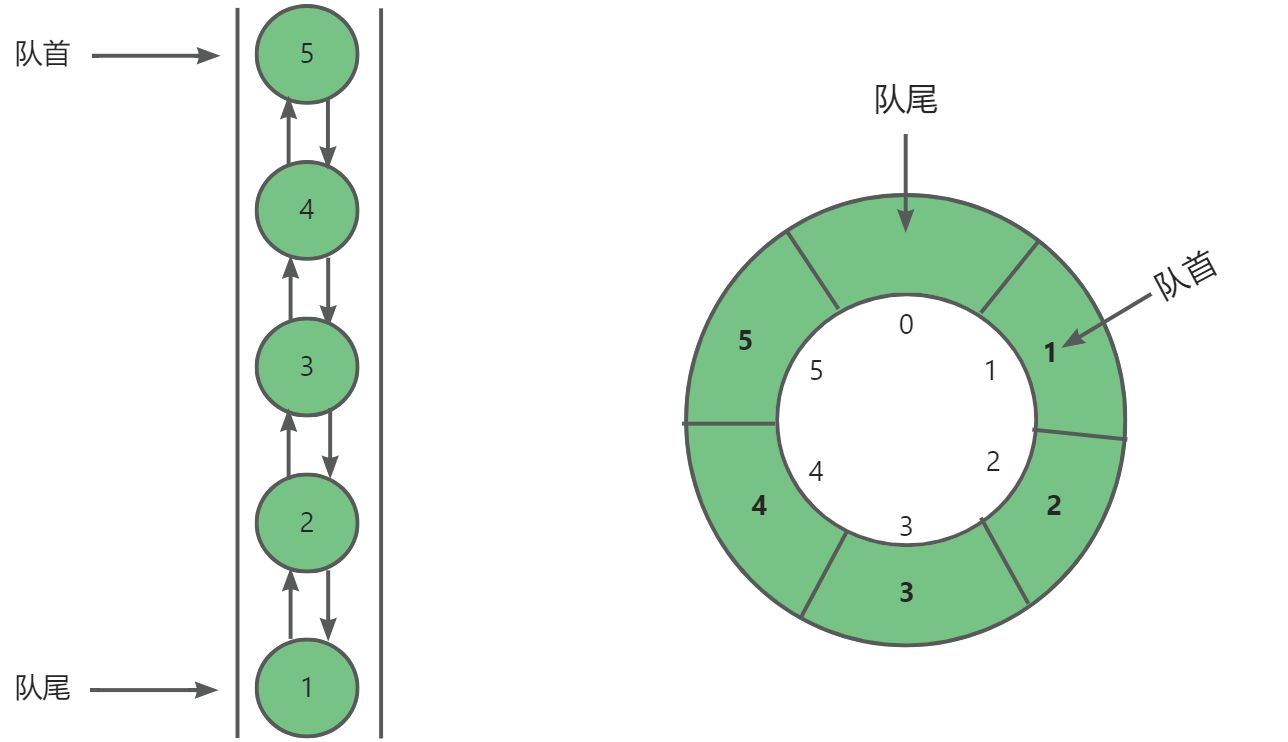
3. 双向队列的功能
- 队列的初始化。
- 判断队列是否为空。。
- 返回队头与队尾的元素。
- 返回队列的大小。
- 入队与出队。
- 打印队列的元素。
- 销毁队列。
4. 双向队列的声明
4.1. 链式队
双向队列与普通队列的声明区别就在于双向队列是基于双向链表的方式实现。
typedef int QDataType;
typedef struct DuListNode
{QDataType data;struct Node* prev;struct Node* next;
}DuListNode;typedef struct Deque
{size_t size;DuListNode* front;DuListNode* rear;
}Deque;
4.2. 循环队
循环队列的实现方式与普通队列差不多。
typedef int QDataType;
#define MAXSIZE 50 //定义元素的最大个数
typedef struct {QDataType *data;int front; //头指针int rear; //尾指针
}Deque;
5. 队列的初始化
5.1. 链式队
void DequeInit(Deque* d)//初始化
{assert(d);d->front = NULL;d->rear = NULL;d->size = 0;
}
5.2. 循环队
void DequeInit(Deque* d)//初始化
{d->data = (QDataType*)malloc(sizeof(QDataType )* MAXSIZE);if (d->data == NULL){perror("malloc fail:");return;}d->front = 0;d->rear = 0;
}
5.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:链式队空间是一个固定大小,空间复杂度为O(1)。而需要开辟整个队列的大小,空间复杂度为O(N)。
6. 判断队列是否为空
6.1. 链式队
bool DequeEmpty(Deque* d)//判断是否为空
{assert(d);return (d->front == NULL) && (d->rear == NULL);
}
6.2. 循环队
bool DequeEmpty(Deque* d)//判断是否为空
{assert(d);return d->front == d->rear;
}
6.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)。
7. 判断队列是否为满
7.1. 链式队
链式队并不需要判断。
7.2. 循环队
为什么要取模操作,可以参考一下上一篇普通队列的实现,同下。
bool DequeFull(Deque* d)//判断队列是否满
{assert(d);return (d->rear + 1) % MAXSIZE == d->front;
}
8. 返回队头与队尾的元素
8.1. 链式队
QDataType DequeFront(Deque* d)//获取队头元素
{assert(d);assert(!DequeEmpty(d));return d->front->data;
}
QDataType DequeBack(Deque* d)//获取队尾元素
{assert(d);assert(!DequeEmpty(d));return d->rear->data;
}
8.2. 循环队
QDataType DequeFront(Deque* d)//获取队头元素
{assert(d);assert(!DequeEmpty(d));return d->data[d->front];
}
QDataType DequeBack(Deque* d)//获取队尾元素
{assert(d);assert(!DequeEmpty(d));return d->data[(d->rear-1+MAXSIZE)%MAXSIZE];
}
8.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
9. 返回队列的大小
9.1. 链式队
size_t DequeSize(Deque* d)//队列长度
{return d->size;
}
9.2. 循环队
size_t DequeSize(Deque* d)//获取队列长度
{assert(d);return (d->rear - d->front + MAXSIZE) % MAXSIZE;
}
9.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
10. 入队
10.1. 链式队
10.1.1. 队头入队
void DequeFrontPush(Deque* d, QDataType x)//队首入队
{assert(d);DuListNode* newnode = (DuListNode*)malloc(sizeof(DuListNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;if (d->front == NULL){d->front = d->rear = newnode;}else{d->front->prev = newnode;newnode->next = d->front;d->front = newnode;}d->size++;
}
10.1.2. 队尾入队
void DequeRearPush(Deque* d, QDataType x)//队尾入队
{assert(d);DuListNode* newnode = (DuListNode*)malloc(sizeof(DuListNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;if (d->front == NULL){d->front = d->rear = newnode;}else{d->rear->next = newnode;newnode->prev = d->rear;d->rear = newnode;}d->size++;
}
10.2. 循环队
入队需要提前判断队列是否为满。
10.2.1. 队头入队
void DequeFrontPush(Deque* d, QDataType x)//队首入队
{assert(d);if (DequeFull(d)){printf("队列已满\n");return;}d->data[(d->front - 1 + MAXSIZE) % MAXSIZE]=x;d->front = (d->front - 1 + MAXSIZE) % MAXSIZE;
}
10.2.2. 队尾入队
void DequeRearPush(Deque* d, QDataType x)//队尾入队
{assert(d);if (DequeFull(d)){printf("队列已满\n");return;}d->data[d->rear] = x;d->rear = (d->rear + 1) % MAXSIZE;
}
10.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
11. 出队
11.1. 链式队
出队需要提前判断队列是否为空。
11.1.1. 队头出队
void DequeFrontPop(Deque* d)//队首出队
{assert(d);assert(!DequeEmpty(d));//1.只有一个结点if (d->front == d->rear){free(d->front);d->front = d->rear = NULL;}//2.有多个结点else{DuListNode* next = d->front->next;next->prev = NULL;d->front->next = NULL;free(d->front);d->front = next;}d->size--;
}
11.1.2. 队尾出队
void DequeRearPop(Deque* d)//队尾出队
{assert(d);assert(!DequeEmpty(d));//1.只有一个结点if (d->front == d->rear){free(d->front);d->front = d->rear = NULL;}else{DuListNode* prev = d->rear->prev;prev->next = NULL;d->rear->prev = NULL;free(d->rear);d->rear = prev;}d->size--;
}
11.2. 循环队
11.2.1. 队头出队
void DequeFrontPop(Deque* d)//队首出队
{assert(d);assert(!DequeEmpty(d));d->front = (d->front + 1) % MAXSIZE;
}
11.2.2. 队尾出队
void DequeRearPop(Deque* d)//队尾出队
{assert(d);assert(!DequeEmpty(d));d->rear = (d->rear - 1+MAXSIZE) % MAXSIZE;
}
11.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
12. 打印队列元素
12.1. 链式队
void DequePrint(Deque* d)//打印队列元素
{assert(d);DuListNode* cur = d->front;DuListNode* tail = d->rear;printf("队头:");while (cur != tail->next){printf("%d<=>", cur->data);cur = cur->next;}printf("队尾\n");
}
12.2. 循环队
void DequePrint(Deque* d)//打印队列元素
{assert(d);int cur = d->front;printf("队头->");while (cur != d->rear){printf("%d->", d->data[cur]);cur = (cur + 1) % MAXSIZE;}printf("队尾\n");}
12.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列都需要遍历这个队列,所以时间复杂度为O(N)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
13. 销毁队列
13.1. 链式队
void DequeDestroy(Deque* d)//销毁队列
{assert(d);DuListNode* cur = d->front;while (cur){DuListNode* del = cur;cur = cur->next;free(del);del = NULL;}d->front = d->rear = NULL;
}
13.2. 循环队
void DequeDestroy(Deque* d)//销毁队列
{assert(d);free(d->data);d->data = NULL;d->front = d->rear = 0;
}
13.3. 复杂度分析
- 时间复杂度:无论是链式队还是循环队列花费时间都是一个常数,所以时间复杂度为O(1)。
- 空间复杂度:无论是链式队还是循环队列花费空间都是一个固定大小,所以空间复杂度为O(1)
14. 对比与应用
14.1. 对比
双向队列的两种实现方式的效果与普通队列实现差不多,这里就不在一一赘述。
14.2. 应用
双向队列兼备队列与栈的性质,所以可以应用于这两种数据结构的所有应用场景。
此外它应用于撤销的一种情景:通常情况下,撤销是以栈的方式实现,当我们每次更改时就入栈,撤销就出栈。但是我们知道系统给与栈的空间是有限的,我们不可能一直入栈。当入栈超过一个限度时,我们就用过删除栈底的数据,这时栈这个数据结构就无法满足需求。所以这时我们可以使用双向队列来实现。
15. 完整代码
15.1. 链式队
15.1.1. Deque.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int QDataType;
typedef struct DuListNode
{QDataType data;struct Node* prev;struct Node* next;
}DuListNode;typedef struct Deque
{size_t size;DuListNode* front;DuListNode* rear;
}Deque;
void DequeInit(Deque* d);//初始化
bool DequeEmpty(Deque* d);//判断是否为空
QDataType DequeFront(Deque* d);//获取队头元素
QDataType DequeBack(Deque* d);//获取队尾元素
size_t DequeSize(Deque* d);//获取队列长度
void DequeFrontPush(Deque* d, QDataType x);//队首入队
void DequeRearPush(Deque* d, QDataType x);//队尾入队
void DequeFrontPop(Deque* d);//队首出队
void DequeRearPop(Deque* d);//队尾出队
void DequePrint(Deque* d);//打印队列元素
void DequeDestroy(Deque* d);//销毁队列
15.1.2. Deque.c
#define _CRT_SECURE_NO_WARNINGS 1
#include"Deque.h"
void DequeInit(Deque* d)//初始化
{assert(d);d->front = NULL;d->rear = NULL;d->size = 0;
}
bool DequeEmpty(Deque* d)//判断是否为空
{assert(d);return (d->front == NULL) && (d->rear == NULL);
}
QDataType DequeFront(Deque* d)//获取队头元素
{assert(d);assert(!DequeEmpty(d));return d->front->data;
}
QDataType DequeBack(Deque* d)//获取队尾元素
{assert(d);assert(!DequeEmpty(d));return d->rear->data;
}
size_t DequeSize(Deque* d)//队列长度
{return d->size;
}
void DequeFrontPush(Deque* d, QDataType x)//队首入队
{assert(d);DuListNode* newnode = (DuListNode*)malloc(sizeof(DuListNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;if (d->front == NULL){d->front = d->rear = newnode;}else{d->front->prev = newnode;newnode->next = d->front;d->front = newnode;}d->size++;
}
void DequeRearPush(Deque* d, QDataType x)//队尾入队
{assert(d);DuListNode* newnode = (DuListNode*)malloc(sizeof(DuListNode));if (newnode == NULL){perror("malloc fail");return;}newnode->data = x;newnode->next = NULL;newnode->prev = NULL;if (d->front == NULL){d->front = d->rear = newnode;}else{d->rear->next = newnode;newnode->prev = d->rear;d->rear = newnode;}d->size++;
}
void DequeFrontPop(Deque* d)//队首出队
{assert(d);assert(!DequeEmpty(d));//1.只有一个结点if (d->front == d->rear){free(d->front);d->front = d->rear = NULL;}//2.有多个结点else{DuListNode* next = d->front->next;next->prev = NULL;d->front->next = NULL;free(d->front);d->front = next;}d->size--;
}
void DequeRearPop(Deque* d)//队尾出队
{assert(d);assert(!DequeEmpty(d));//1.只有一个结点if (d->front == d->rear){free(d->front);d->front = d->rear = NULL;}else{DuListNode* prev = d->rear->prev;prev->next = NULL;d->rear->prev = NULL;free(d->rear);d->rear = prev;}d->size--;
}
void DequePrint(Deque* d)//打印队列元素
{assert(d);DuListNode* cur = d->front;DuListNode* tail = d->rear;printf("队头:");while (cur != tail->next){printf("%d<=>", cur->data);cur = cur->next;}printf("队尾\n");
}
void DequeDestroy(Deque* d)//销毁队列
{assert(d);DuListNode* cur = d->front;while (cur){DuListNode* del = cur;cur = cur->next;free(del);del = NULL;}d->front = d->rear = NULL;
}
15.2. 循环队
15.2.1. Deque.h
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int QDataType;
#define MAXSIZE 50 //定义元素的最大个数
typedef struct {QDataType *data;int front; //头指针int rear; //尾指针
}Deque;void DequeInit(Deque* d);//初始化
bool DequeEmpty(Deque* d);//判断是否为空
bool DequeFull(Deque* d);//判断队列是否满
QDataType DequeFront(Deque* d);//获取队头元素
QDataType DequeBack(Deque* d);//获取队尾元素
size_t DequeSize(Deque* d);//获取队列长度
void DequeFrontPush(Deque* d, QDataType x);//队首入队
void DequeRearPush(Deque* d, QDataType x);//队尾入队
void DequeFrontPop(Deque* d);//队首出队
void DequeRearPop(Deque* d);//队尾出队
void DequePrint(Deque* d);//打印队列元素
void DequeDestroy(Deque* d);//销毁队列
15.2.2. Deque.c
void DequeInit(Deque* d)//初始化
{d->data = (QDataType*)malloc(sizeof(QDataType )* MAXSIZE);if (d->data == NULL){perror("malloc fail:");return;}d->front = 0;d->rear = 0;
}
bool DequeEmpty(Deque* d)//判断是否为空
{assert(d);return d->front == d->rear;
}
bool DequeFull(Deque* d)//判断队列是否满
{assert(d);return (d->rear + 1) % MAXSIZE == d->front;
}
QDataType DequeFront(Deque* d)//获取队头元素
{assert(d);assert(!DequeEmpty(d));return d->data[d->front];
}
QDataType DequeBack(Deque* d)//获取队尾元素
{assert(d);assert(!DequeEmpty(d));return d->data[(d->rear-1+MAXSIZE)%MAXSIZE];
}
size_t DequeSize(Deque* d)//获取队列长度
{assert(d);return (d->rear - d->front + MAXSIZE) % MAXSIZE;
}
void DequeFrontPush(Deque* d, QDataType x)//队首入队
{assert(d);if (DequeFull(d)){printf("队列已满\n");return;}d->data[(d->front - 1 + MAXSIZE) % MAXSIZE]=x;d->front = (d->front - 1 + MAXSIZE) % MAXSIZE;
}
void DequeRearPush(Deque* d, QDataType x)//队尾入队
{assert(d);if (DequeFull(d)){printf("队列已满\n");return;}d->data[d->rear] = x;d->rear = (d->rear + 1) % MAXSIZE;
}
void DequeFrontPop(Deque* d)//队首出队
{assert(d);assert(!DequeEmpty(d));d->front = (d->front + 1) % MAXSIZE;
}
void DequeRearPop(Deque* d)//队尾出队
{assert(d);assert(!DequeEmpty(d));d->rear = (d->rear - 1+MAXSIZE) % MAXSIZE;
}
void DequePrint(Deque* d)//打印队列元素
{assert(d);int cur = d->front;printf("队头->");while (cur != d->rear){printf("%d->", d->data[cur]);cur = (cur + 1) % MAXSIZE;}printf("队尾\n");}
void DequeDestroy(Deque* d)//销毁队列
{assert(d);free(d->data);d->data = NULL;d->front = d->rear = 0;
}
相关文章:

探索数据结构:特殊的双向队列
✨✨ 欢迎大家来到贝蒂大讲堂✨✨ 🎈🎈养成好习惯,先赞后看哦~🎈🎈 所属专栏:数据结构与算法 贝蒂的主页:Betty’s blog 1. 双向队列的定义 **双向队列(double‑ended queue)**是一种特殊的队列…...

16_I2C库函数
I2C库函数 1.void I2C_DeInit(I2C_TypeDef* I2Cx);2.void I2C_Init(I2C_TypeDef* I2Cx, I2C_InitTypeDef* I2C_InitStruct);3.void I2C_StructInit(I2C_InitTypeDef* I2C_InitStruct);4.void I2C_Cmd(I2C_TypeDef* I2Cx, FunctionalState NewState);5.void I2C_DMACmd(I2C_Type…...

十八、Rust gRPC 多 proto 演示
十八、Rust gRPC 多 proto 演示 网上及各官方资料,基本是一个 proto 文件,而实际项目,大多是有层级结构的多 proto 文件形式,本篇文章 基于此诉求,构建一个使用多 proto 文件的 rust grpc 使用示例。 关于 grpc 的实现…...

【Linux】Linux64位环境下编译32位报错skipping incompatible的解决办法
本文首发于 ❄️慕雪的寒舍 问题 如题,当我尝试在wsl2的ubuntu中使用-m32选项编译32位程序的时候,出现了下面的两种报错 ❯ g -m32 test.cpp -o test1 && ./test1 In file included from test.cpp:1: /usr/include/stdio.h:27:10: fatal error…...

vue指令v-model
<!DOCTYPE html> <html lang"en"> <head> <meta charset"UTF-8"> <meta name"viewport" content"widthdevice-width, initial-scale1.0"> <title>vue指令v-model</title> </head>…...

CentOS安装MySQL数据库
一、更新yum源 #下载对应repo文件 wget -O CentOS-Base.repo http://mirrors.aliyun.com/repo/Centos-8.repo #清除缓存 yum clean all #生成新缓存 yum makecache #更新 yum update -y 二、安装MySQL #获取源 wget http://repo.mysql.com/mysql80-community-release-el7-3.…...

从B2B转向B2B2C模式:工业品牌史丹利百得的转型历程
图片来源:Twitter 在当今数据驱动的营销环境中,企业努力更好了解客户,并在整个客户旅程中提供个性化体验。史丹利百得(Stanley Black & Decker)是一家领先的工具和工业设备供应商,近年来开始重大转型。…...
Redis群集模式和rsync远程同步
一、Redis群集模式 1.1 概念 1.2 作用 1.2.1 Redis集群的数据分片 1.2.2 Redis集群的主从复制模型 1.3 搭建Redis 群集模式 1.3.1 开启群集功能 1.3.2 启动redis节点 1.3.3 启动集群 1.3.4 测试群集 二、rsync远程同步 2.1 概念 2.2 同步方式 2.3 备份的方式 2.4…...

JAVA—抽象—定义抽象类Converter及其子类WeightConverter
同样,我们由这道题引出抽象类,抽象方法这个概念。 按下面要求定义类Converter及其子类WeightConverter 定义抽象类:Converter: 定义一个抽象类Converter,表示换算器,其定义的如下: 一个私有…...
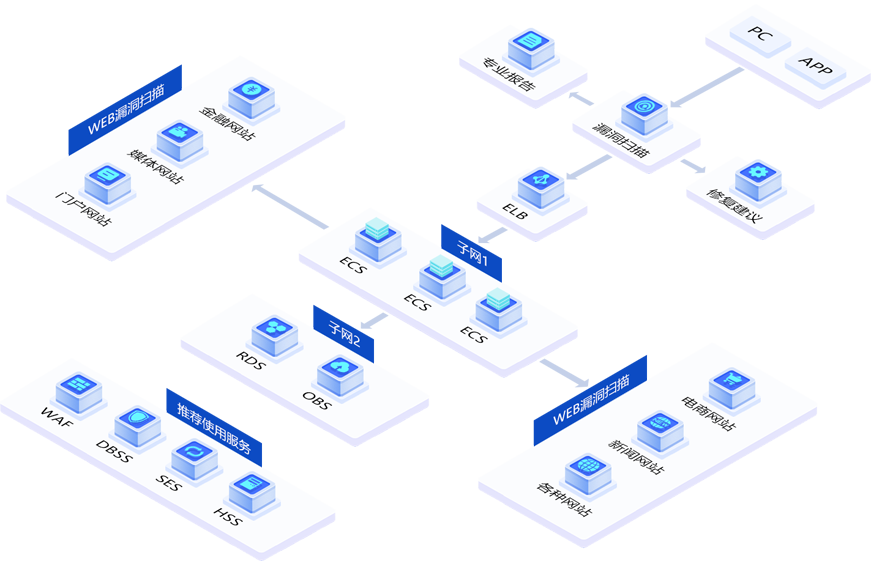
面对复杂多变的网络攻击,企业应如何守护网络安全
企业上云,即越来越多的企业把业务和数据,迁移到云端。随着云计算、大数据、物联网、人工智能等技术的发展,用户、应用程序和数据无处不在,企业之间的业务边界逐渐被打破,网络攻击愈演愈烈,手段更为多。 当前…...

计算机网络练习-计算机网络概述与性能指标
计算机网络概述 ----------------------------------------------------------------------------------------------------------------------------- 1. 计算机网络最据本的功能的是( )。 1,差错控制 Ⅱ.路由选择 Ⅲ,分布式处理 IV.传输控制 …...

vite vue3 ts import.meta在vscode中报错
问题描述:开发使用的框架为vitevue3ts,在开发过程中莫名其妙报仅当“--module”选项为“es2020”、“esnext”或“系统”时才允许使用“import.meta”元属性 问题解决: 通过更改tsconfig.json的module为esnext,es2022等࿰…...
)
Java synchronized(详细)
synchronized 一,介绍 在Java中,synchronized关键字用于解决多线程并发访问共享资源时可能出现的线程安全问题。当多个线程同时访问共享资源时,如果没有合适的同步机制,可能会导致以下问题: 竞态条件(…...

算法设计与分析实验报告python实现(排序算法、三壶谜题、交替放置的碟子、带锁的门)
一、 实验目的 1.加深学生对算法设计方法的基本思想、基本步骤、基本方法的理解与掌握; 2.提高学生利用课堂所学知识解决实际问题的能力; 3.提高学生综合应用所学知识解决实际问题的能力。 二、实验任务 1、排序算法…...

实训问题总结——ajax用get可以成功调用controller方法,用POST就出404错误
因为传输密码时必须用POST。 还有用GET传输参数,说有非法字符,想试试POST是否可以解决。 404错误的三个大致原因,1:找不到对的请求路径,2:请求方式错误,3、请求参数错误。 后来可以调用了。但…...
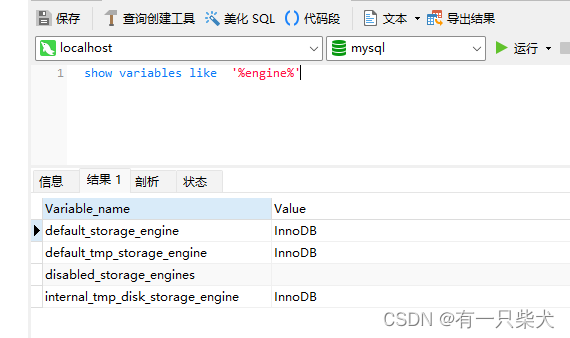
1、认识MySQL存储引擎吗?
目录 1、MySQL存储引擎有哪些? 2、默认的存储引擎是哪个? 3、InnoDB和MyISAM有什么区别吗? 3.1、关于事务 3.2、关于行级锁 3.3、关于外键支持 3.4、关于是否支持MVCC 3.5、关于数据安全恢复 3.6、关于索引 3.7、关于性能 4、如何…...

微信小程序媒体查询
在微信小程序中,media媒体查询不支持screen关键字,因为小程序页面是再webview中渲染的,而不是在浏览器中渲染的。 在设置样式时,可以使用 wxss 文件中的 media 规则来根据屏幕宽度或高度设置不同的样式。 device-width:设备屏幕…...

前端(动态雪景背景+动态蝴蝶)
1.CSS样式 <style>html, body, a, div, span, table, tr, td, strong, ul, ol, li, h1, h2, h3, p, input {font-weight: inherit;font-size: inherit;list-style: none;border-spacing: 0;border: 0;border-collapse: collapse;text-decoration: none;padding: 0;margi…...

软考-系统集成项目管理中级-新一代信息技术
本章历年考题分值统计 本章重点常考知识点汇总清单(掌握部分可直接理解记忆) 本章历年考题及答案解析 32、2019 年上半年第 23 题 云计算通过网络提供可动态伸缩的廉价计算能力,(23)不属于云计算的特点。 A.虚拟化 B.高可扩展性 C.按需服务 D.优化本地存储 【参考…...
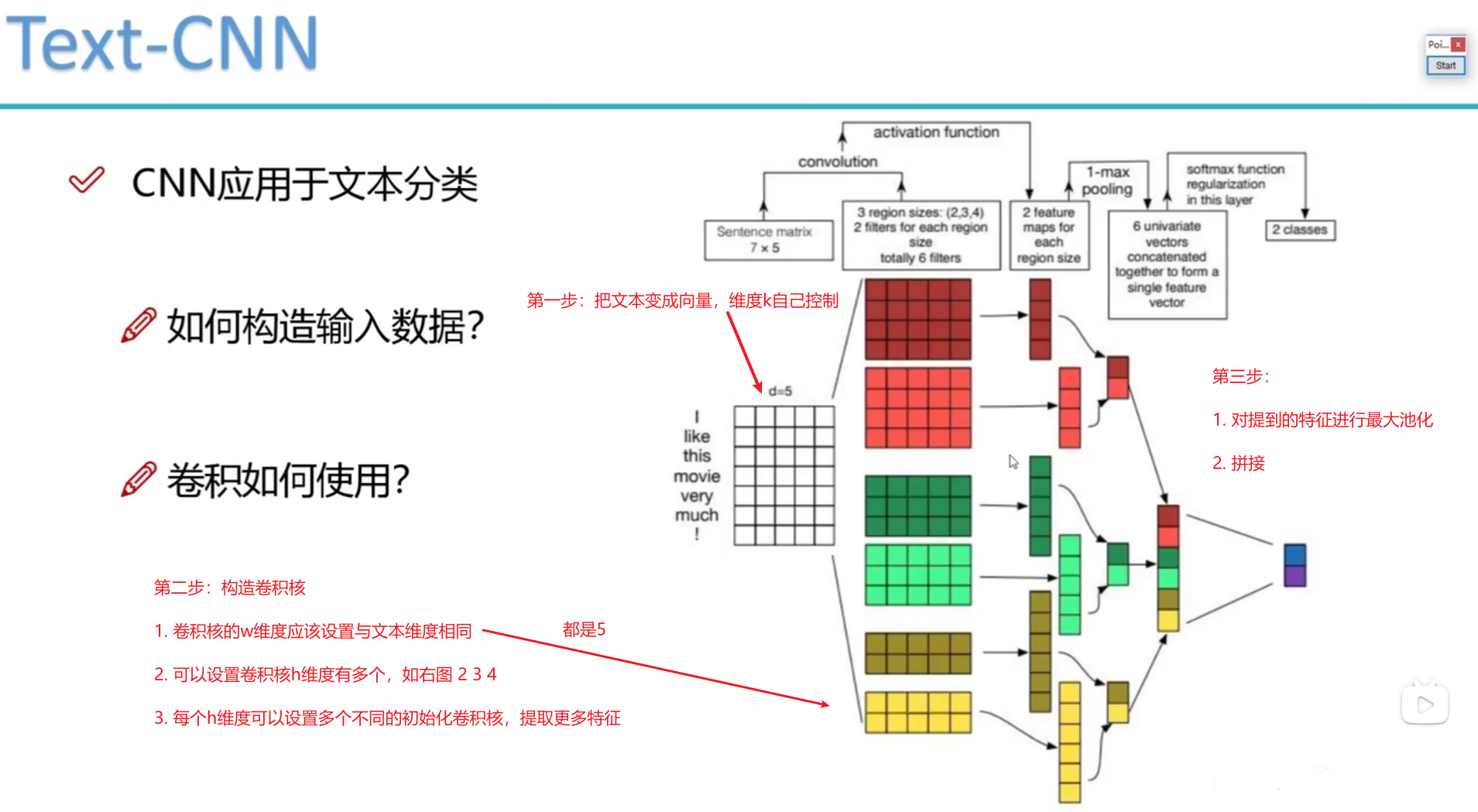
【卷积神经网络进展】
打基础日常记录 CNN基础知识1. 感知机2. DNN 深度神经网络(全连接神经网络)DNN 与感知机的区别DNN特点,全连接神经网络DNN前向传播和反向传播 3. CNN结构【提取特征分类】4. CNN应用于文本 CNN基础知识 1. 感知机 单层感知机就是一个二分类…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

ArcGIS Pro制作水平横向图例+多级标注
今天介绍下载ArcGIS Pro中如何设置水平横向图例。 之前我们介绍了ArcGIS的横向图例制作:ArcGIS横向、多列图例、顺序重排、符号居中、批量更改图例符号等等(ArcGIS出图图例8大技巧),那这次我们看看ArcGIS Pro如何更加快捷的操作。…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

Linux部署私有文件管理系统MinIO
最近需要用到一个文件管理服务,但是又不想花钱,所以就想着自己搭建一个,刚好我们用的一个开源框架已经集成了MinIO,所以就选了这个 我这边对文件服务性能要求不是太高,单机版就可以 安装非常简单,几个命令就…...

关于 ffmpeg设置摄像头报错“Could not set video options” 的解决方法
若该文为原创文章,转载请注明原文出处 本文章博客地址:https://hpzwl.blog.csdn.net/article/details/148515355 长沙红胖子Qt(长沙创微智科)博文大全:开发技术集合(包含Qt实用技术、树莓派、三维、OpenCV…...

