0205矩阵分块法-矩阵及其运算-线性代数
文章目录
- 1 分块矩阵的定义
- 2 分块矩阵的运算(性质)
- 3 按列分块与按行分块
- 结语
1 分块矩阵的定义
将矩阵A用若干条纵线和横线分成许多个小矩阵,每一个小矩阵称为A的子快,以子块为元素的形式上的矩阵称为分块矩阵。
2 分块矩阵的运算(性质)
-
设矩阵A与B的行数相同,列数相同,采用相同的分块法,有
A = ( A 11 ⋯ A 1 r ⋮ ⋮ A s 1 ⋯ A s r ) , B = ( B 11 ⋯ B 1 r ⋮ ⋮ B s 1 ⋯ B s r ) A=\begin{pmatrix} A_{11}&\cdots&A_{1r}\\ \vdots&&\vdots\\ A_{s1}&\cdots&A_{sr} \end{pmatrix} ,B=\begin{pmatrix} B_{11}&\cdots&B_{1r}\\ \vdots&&\vdots\\ B_{s1}&\cdots&B_{sr} \end{pmatrix}\\ A= A11⋮As1⋯⋯A1r⋮Asr ,B= B11⋮Bs1⋯⋯B1r⋮Bsr
其中 A i j 与 B i j A_{ij}与B_{ij} Aij与Bij行数相同,列数相同,那么
A + B = ( A 11 + B 11 ⋯ A 1 r + B 1 r ⋮ ⋮ A s 1 + B s 1 ⋯ A s r + B s r ) A+B=\begin{pmatrix} A_{11}+B_{11}&\cdots&A_{1r}+B_{1r}\\ \vdots&&\vdots\\ A_{s1}+B_{s1}&\cdots&A_{sr}+B_{sr} \end{pmatrix} A+B= A11+B11⋮As1+Bs1⋯⋯A1r+B1r⋮Asr+Bsr -
设
A = ( A 11 ⋯ A 1 r ⋮ ⋮ A s 1 ⋯ A s r ) , λ 为数,那么 A=\begin{pmatrix} A_{11}&\cdots&A_{1r}\\ \vdots&&\vdots\\ A_{s1}&\cdots&A_{sr} \end{pmatrix} ,\lambda为数,那么 A= A11⋮As1⋯⋯A1r⋮Asr ,λ为数,那么λ A = ( λ A 11 ⋯ λ A 1 r ⋮ ⋮ λ A s 1 ⋯ λ A s r ) \lambda A=\begin{pmatrix} \lambda A_{11}&\cdots&\lambda A_{1r}\\ \vdots&&\vdots\\ \lambda A_{s1}&\cdots&\lambda A_{sr} \end{pmatrix} λA= λA11⋮λAs1⋯⋯λA1r⋮λAsr
-
设A位 m × l m\times l m×l矩阵,B位 l × n l\times n l×n矩阵,分块成
A = ( A 11 ⋯ A 1 t ⋮ ⋮ A s 1 ⋯ A s t ) , B = ( A 11 ⋯ A 1 r ⋮ ⋮ A t 1 ⋯ A t r ) A=\begin{pmatrix} A_{11}&\cdots&A_{1t}\\ \vdots&&\vdots\\ A_{s1}&\cdots&A_{st} \end{pmatrix} ,B=\begin{pmatrix} A_{11}&\cdots&A_{1r}\\ \vdots&&\vdots\\ A_{t1}&\cdots&A_{tr} \end{pmatrix} A= A11⋮As1⋯⋯A1t⋮Ast ,B= A11⋮At1⋯⋯A1r⋮Atr
其中 A i 1 , A i 2 , ⋯ , A i t A_{i1},A_{i2},\cdots,A_{it} Ai1,Ai2,⋯,Ait的列数分别等于 B 1 j , B 2 j , ⋯ , B t j B_{1j},B_{2j},\cdots,B_{tj} B1j,B2j,⋯,Btj的行数,那么
A B = ( C 11 ⋯ C 1 r ⋮ ⋮ C s 1 ⋯ C s r ) AB=\begin{pmatrix} C_{11}&\cdots&C_{1r}\\ \vdots&&\vdots\\ C_{s1}&\cdots&C_{sr} \end{pmatrix} AB= C11⋮Cs1⋯⋯C1r⋮Csr
其中
C i j = ∑ k = 1 t A i k B k j ( i = 1 , ⋯ , s ; j = 1 , ⋯ , r ) C_{ij}=\sum_{k=1}^tA_{ik}B_{kj}(i=1,\cdots,s;j=1,\cdots,r) Cij=k=1∑tAikBkj(i=1,⋯,s;j=1,⋯,r) -
设
A = ( A 11 ⋯ A 1 r ⋮ ⋮ A s 1 ⋯ A s r ) ,则 A T = ( A 11 T ⋯ A s 1 T ⋮ ⋮ A 1 r T ⋯ A s r T ) A=\begin{pmatrix} A_{11}&\cdots&A_{1r}\\ \vdots&&\vdots\\ A_{s1}&\cdots&A_{sr} \end{pmatrix} ,则A^T=\begin{pmatrix} A_{11}^T&\cdots&A_{s1}^T\\ \vdots&&\vdots\\ A_{1r}^T&\cdots&A_{sr}^T \end{pmatrix} A= A11⋮As1⋯⋯A1r⋮Asr ,则AT= A11T⋮A1rT⋯⋯As1T⋮AsrT -
设A为n阶方阵,若A的分块矩阵只有在对角线上有非零子块,其余子块都为零矩阵,且在对角线上的子块都是方阵,即
A = ( A 1 O A 2 ⋱ O A s ) A=\begin{pmatrix} A_{1}&&&O\\ &A_2&&\\ &&\ddots&\\ O&&&A_s \end{pmatrix} A= A1OA2⋱OAs
其中 A i ( i = 1 , 2 , ⋯ , s ) A_i(i=1,2,\cdots,s) Ai(i=1,2,⋯,s)都方阵,那么称A为分块对角矩阵。分块对角矩阵的行列式有以下性质
∣ A ∣ = ∣ A 1 ∣ ∣ A 2 ∣ ⋯ ∣ A s ∣ |A|=|A_1||A_2|\cdots |A_s| ∣A∣=∣A1∣∣A2∣⋯∣As∣
由此性质可知,若 ∣ A i ∣ ≠ 0 ( i = i , 2 , ⋯ , s ) |A_i|\not=0(i=i,2,\cdots,s) ∣Ai∣=0(i=i,2,⋯,s),则 ∣ A ∣ ≠ 0 |A|\not=0 ∣A∣=0,并有
A − 1 = ( A 1 − 1 O A 2 − 1 ⋱ O A s − 1 ) A^{-1}=\begin{pmatrix} A_{1}^{-1}&&&O\\ &A_2^{-1}&&\\ &&\ddots&\\ O&&&A_s^{-1} \end{pmatrix} A−1= A1−1OA2−1⋱OAs−1
例18 设
A = ( 5 0 0 0 3 1 0 2 1 ) ,求 A − 1 A=\begin{pmatrix} 5&0&0\\ 0&3&1\\ 0&2&1 \end{pmatrix} ,求A^{-1} A= 500032011 ,求A−1KaTeX parse error: Undefined control sequence: \vline at position 24: …gin{pmatrix} 5&\̲v̲l̲i̲n̲e̲0&0\\ \hdashlin…
3 按列分块与按行分块
m × n m\times n m×n矩阵A有n列,称为矩阵A的n个列向量,若第j列记作
a j = ( a 1 j a 2 j ⋮ a m j ) a_j=\begin{pmatrix} a_{1j}\\ a_{2j}\\ \vdots\\ a_{mj} \end{pmatrix} aj= a1ja2j⋮amj
则A可按列分块位
A = ( a 1 , a 2 , ⋯ , a n ) A=(a_1,a_2,\cdots,a_n) A=(a1,a2,⋯,an)
m × n m\times n m×n矩阵A有m行,称为矩阵A的m个行向量,若第 i i i行记作
α i T = ( a i 1 , a i 2 , ⋯ , a i n ) \alpha_i^T=(a_{i1},a_{i2},\cdots,a_{in}) αiT=(ai1,ai2,⋯,ain)
则A可按行分开为
A = ( α 1 T α 2 T ⋮ α m T ) A=\begin{pmatrix} \alpha_1^T\\ \alpha_2^T\\ \vdots\\ \alpha_m^T \end{pmatrix} A= α1Tα2T⋮αmT
对于矩阵 A = ( a i j ) m × s A=(a_{ij})_{m\times s} A=(aij)m×s与矩阵 B = ( b i j ) s × n B=(b_{ij})_{s\times n} B=(bij)s×n的乘积矩阵 A B = C = ( c i j ) m × n AB=C=(c_{ij})_{m\times n} AB=C=(cij)m×n,若把A按行分成m快,把B案列分成n快,便有
A B = ( α 1 T α 2 T ⋮ α m T ) ( b 1 , b 2 , ⋯ , b n ) = ( α 1 T b 1 α 1 T b 2 ⋯ α 1 T b n α 2 T b 1 α 2 T b 2 ⋯ α 2 T b n ⋮ ⋮ ⋮ α m T b 1 α m T b 2 ⋯ α m T b n ) AB=\begin{pmatrix} \alpha_1^T\\ \alpha_2^T\\ \vdots\\ \alpha_m^T \end{pmatrix} \begin{pmatrix} b_1,b_2,\cdots,b_n\\ \end{pmatrix}\\ =\begin{pmatrix} \alpha_1^Tb_1&\alpha_1^Tb_2&\cdots&\alpha_1^Tb_n\\ \alpha_2^Tb_1&\alpha_2^Tb_2&\cdots&\alpha_2^Tb_n\\ \vdots&\vdots&&\vdots\\ \alpha_m^Tb_1&\alpha_m^Tb_2&\cdots&\alpha_m^Tb_n\\ \end{pmatrix} AB= α1Tα2T⋮αmT (b1,b2,⋯,bn)= α1Tb1α2Tb1⋮αmTb1α1Tb2α2Tb2⋮αmTb2⋯⋯⋯α1Tbnα2Tbn⋮αmTbn
其中
c i j = α i T b j = ( a i 1 , a i 2 , ⋯ , a i s ) ( b 1 j b 2 j ⋮ b s j ) = ∑ k = 1 s a i k b k j c_{ij}=\alpha_i^Tb_j=(a_{i1},a_{i2},\cdots,a_{is}) \begin{pmatrix} b_{1j}\\ b_{2j}\\ \vdots\\ b_{sj} \end{pmatrix} =\sum_{k=1}^sa_{ik}b_{kj} cij=αiTbj=(ai1,ai2,⋯,ais) b1jb2j⋮bsj =k=1∑saikbkj
例19 证明矩阵 A = O A=O A=O的充分必要条件是方阵 A T A = O A^TA=O ATA=O
证明:条件的必要性是显然的 充分性 设 A = ( a i j ) m × n ,把 A 按列分块位 A = ( a 1 , a 2 , ⋯ , a n ) ,则 A T A = ( a 1 T a 2 T ⋮ a n T ) ( a 1 , a 2 , ⋯ , a n ) = ( a 1 T a 1 a 1 T a 2 ⋯ a 1 T a n a 2 T a 1 a 2 T a 2 ⋯ a 2 T a n ⋮ ⋮ ⋮ a n T a 1 a n T a 2 ⋯ a n T a n ) 即 A T A 的 ( i , j ) 元为 a i T a j 因 A T A = O ,故 a i T a j = 0 ( i , j = 1 , 2 , ⋯ , n ) 特殊的,有 a j T a j = 0 ( j = 1 , 2 , ⋯ , n ) 而 a j T a j = ( a 1 j , a 2 j , ⋯ , a m j ) ( a 1 j a 2 j ⋮ a m j ) = a 1 j 2 + a 2 j 2 + ⋯ + a m j 2 = 0 , 得 a 1 j = a 2 j = ⋯ = a m j = 0 即 A = O 证明:条件的必要性是显然的\\ 充分性\\ 设A=(a_{ij})_{m\times n},把A按列分块位A=(a_1,a_2,\cdots,a_n),则\\ A^TA=\begin{pmatrix} a_1^T\\ a_2^T\\ \vdots\\ a_n^T \end{pmatrix} (a_1,a_2,\cdots,a_n)\\ =\begin{pmatrix} a_1^Ta_1&a_1^Ta_2&\cdots&a_1^Ta_n\\ a_2^Ta_1&a_2^Ta_2&\cdots&a_2^Ta_n\\ \vdots&\vdots&&\vdots\\ a_n^Ta_1&a_n^Ta_2&\cdots&a_n^Ta_n\\ \end{pmatrix}\\ 即A^TA的(i,j)元为a_i^Ta_j 因A^TA=O,故\\ a_i^Ta_j=0(i,j=1,2,\cdots,n) 特殊的,有\\ a_j^Ta_j=0(j=1,2,\cdots,n)\\ 而 a_j^Ta_j=(a_{1j},a_{2j},\cdots,a_{mj}) \begin{pmatrix} a_{1j}\\ a_{2j}\\ \vdots\\ a_{mj} \end{pmatrix} =a_{1j}^2+a_{2j}^2+\cdots+a_{mj}^2=0,得\\ a_{1j}=a_{2j}=\cdots=a_{mj}=0\\ 即 A=O 证明:条件的必要性是显然的充分性设A=(aij)m×n,把A按列分块位A=(a1,a2,⋯,an),则ATA= a1Ta2T⋮anT (a1,a2,⋯,an)= a1Ta1a2Ta1⋮anTa1a1Ta2a2Ta2⋮anTa2⋯⋯⋯a1Tana2Tan⋮anTan 即ATA的(i,j)元为aiTaj因ATA=O,故aiTaj=0(i,j=1,2,⋯,n)特殊的,有ajTaj=0(j=1,2,⋯,n)而ajTaj=(a1j,a2j,⋯,amj) a1ja2j⋮amj =a1j2+a2j2+⋯+amj2=0,得a1j=a2j=⋯=amj=0即A=O
线性方程组
{ a 11 x 1 + a 12 x 2 + ⋯ + a 1 n x n = b 1 , a 21 x 1 + a 22 x 2 + ⋯ + a 2 n x n = b 2 , ⋯ ⋯ ⋯ ⋯ a m 1 x 1 + a m 2 x 2 + ⋯ + a m n x n = b m , \begin{cases} a_{11}x_1+a_{12}x_2+\cdots+a_{1n}x_n=b_1,\\ a_{21}x_1+a_{22}x_2+\cdots+a_{2n}x_n=b_2,\\ \cdots\cdots\cdots\cdots\\ a_{m1}x_1+a_{m2}x_2+\cdots+a_{mn}x_n=b_m,\\ \end{cases} ⎩ ⎨ ⎧a11x1+a12x2+⋯+a1nxn=b1,a21x1+a22x2+⋯+a2nxn=b2,⋯⋯⋯⋯am1x1+am2x2+⋯+amnxn=bm,
它的矩阵乘积形式为
A m × n x n × 1 = b m × 1 A_{m\times n}x_{n\times 1}=b_{m\times 1} Am×nxn×1=bm×1
上式中,把A案列分块,把x按行分块,有分块矩阵的乘法有
( a 1 , a 2 , ⋯ , a n ) ( x 1 , x 2 , ⋮ x n ) = b , 即 x 1 a 1 + x 2 a 2 + ⋯ + x n a n = b (a_1,a_2,\cdots,a_n) \begin{pmatrix} x_1,\\ x_2,\\ \vdots\\ x_n \end{pmatrix} =b,即\\ x_1a_1+x_2a_2+\cdots+x_na_n=b (a1,a2,⋯,an) x1,x2,⋮xn =b,即x1a1+x2a2+⋯+xnan=b
其实方程组表成
( a 11 a 21 ⋮ a m 1 ) x 1 + ( a 12 a 22 ⋮ a m 2 ) x 2 + ⋯ ( a 1 n a 2 n ⋮ a m n ) x n = ( b 1 b 2 ⋮ b m ) \begin{pmatrix} a_{11}\\ a_{21}\\ \vdots\\ a_{m1} \end{pmatrix}x_1 +\begin{pmatrix} a_{12}\\ a_{22}\\ \vdots\\ a_{m2} \end{pmatrix}x_2 +\cdots \begin{pmatrix} a_{1n}\\ a_{2n}\\ \vdots\\ a_{mn} \end{pmatrix}x_n =\begin{pmatrix} b_1\\ b_2\\ \vdots\\ b_m \end{pmatrix} a11a21⋮am1 x1+ a12a22⋮am2 x2+⋯ a1na2n⋮amn xn= b1b2⋮bm
结语
❓QQ:806797785
⭐️文档笔记地址 https://github.com/gaogzhen/math
参考:
[1]同济大学数学系.工程数学.线性代数 第6版 [M].北京:高等教育出版社,2014.6.p46-52.
[2]同济六版《线性代数》全程教学视频[CP/OL].2020-02-07.p12.
相关文章:

0205矩阵分块法-矩阵及其运算-线性代数
文章目录 1 分块矩阵的定义2 分块矩阵的运算(性质)3 按列分块与按行分块 结语 1 分块矩阵的定义 将矩阵A用若干条纵线和横线分成许多个小矩阵,每一个小矩阵称为A的子快,以子块为元素的形式上的矩阵称为分块矩阵。 2 分块矩阵的运算…...
1、java语法入门(找工作版)
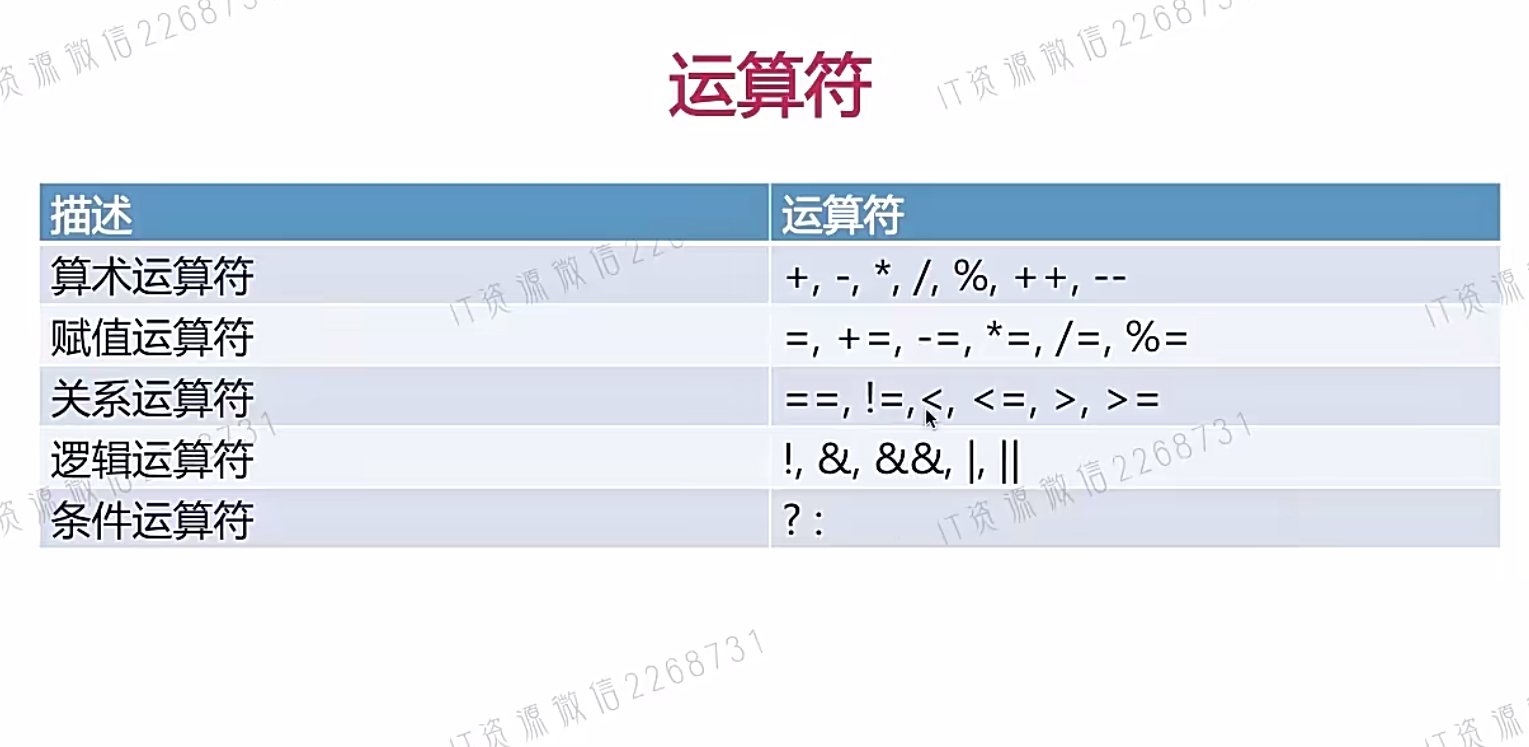
文章目录 一、Java简介二、Java常量与变量1、标识符2、关键字3、变量4、类的命名规则5、数据类型6、基本数据类型字面值7、变量的定义与初始化8、ASCII码和Unicode编码9、转义字符10、类型转换11、常量 三、Java运算符1、算术运算符2、赋值运算符3、关系运算符4、逻辑运算符5、…...

arm的状态寄存器
目录 一、arm 的 PSRs二、CPSR2.1 CPSR_cxsf 三、SPSR四、APSR 一、arm 的 PSRs arm 中有很多程序状态寄存器(Program Status Registers,PSRs)用于存储处理器的状态信息,包括 CPSR\SPSR\FPSR\APSR 等: CPSRÿ…...

2024 蓝桥打卡Day34
20240406蓝桥杯备赛 1、学习蓝桥云课省赛冲刺课 【1-手写与思维】【2-递归与递推】2、学习蓝桥云课Java省赛无忧班 【1-语言基础】3、代码练习字符串排序大小写转换 (ccfcsp之前要是学了我就能上200了 啊啊啊啊 错过啊)斐波那契数列 递归解法纸张尺寸问题…...
华为海思校园招聘-芯片-数字 IC 方向 题目分享——第九套
华为海思校园招聘-芯片-数字 IC 方向 题目分享(有参考答案)——第九套 部分题目分享,完整版获取(WX:didadidadidida313,加我备注:CSDN huawei数字芯片题目,谢绝白嫖哈) 单选 1&…...

如何创建虚拟环境打包py文件
Python 项目通常依赖于特定的库和版本。不同的项目可能依赖于相同库的不同版本,这可能导致冲突。使用虚拟环境,你可以为每个项目创建一个独立的 Python 环境,每个环境都有自己的库和版本,从而避免了依赖冲突。 采用虚拟环境打包P…...
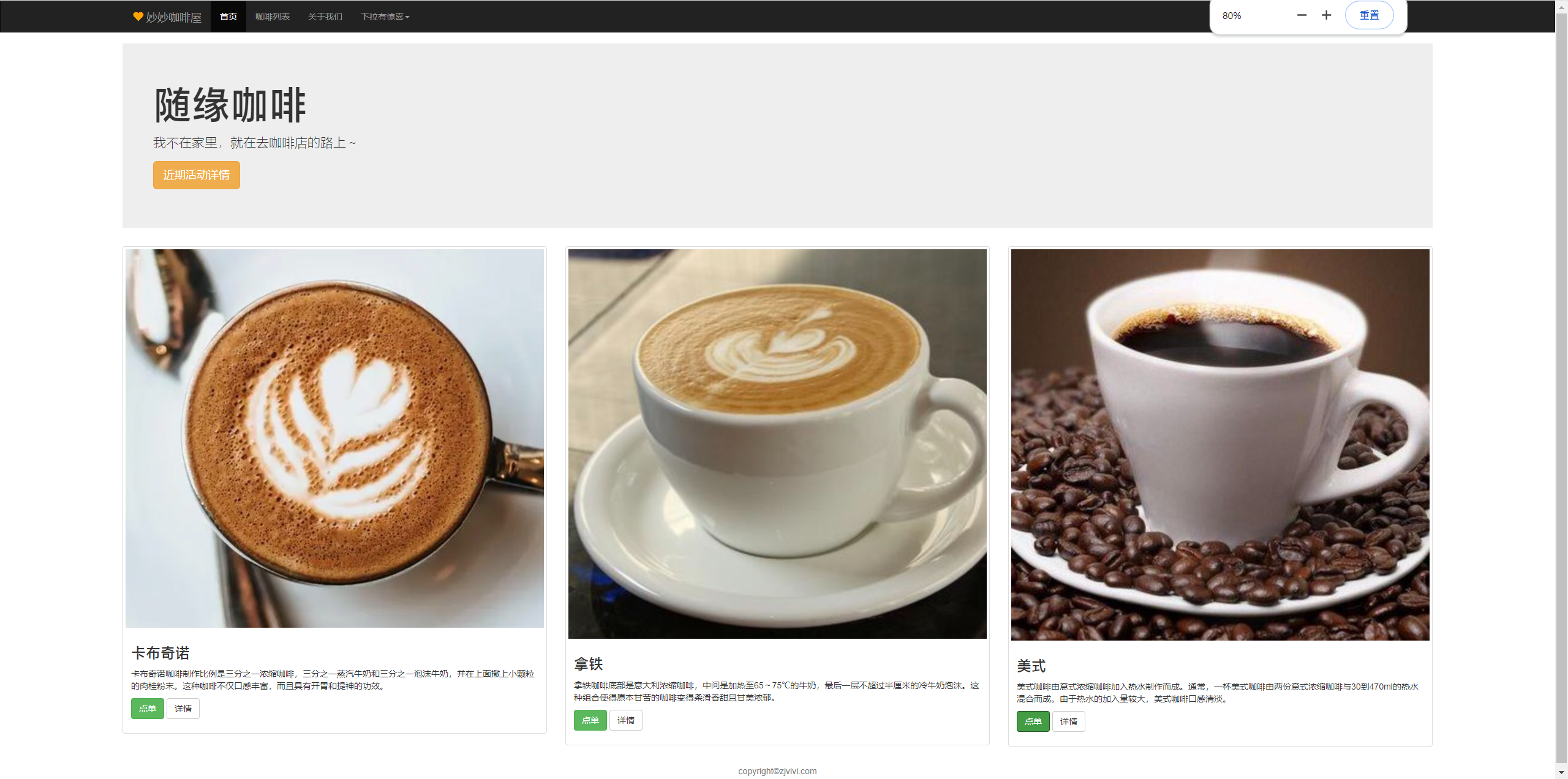
CSS 学习笔记 总结
CSS 布局方式 • 表格布局 • 元素定位 • 浮动布局(注意浮动的负效应) • flex布局 • grid布局(感兴趣的可以看下菜鸟教程) 居中设置 元素水平居中 • 设置宽度后,margin设置为auto • 父容器设置text-alig…...
基于Swin Transformers的乳腺癌组织病理学图像多分类
乳腺癌的非侵入性诊断程序涉及体检和成像技术,如乳房X光检查、超声检查和磁共振成像。成像程序对于更全面地评估癌症区域和识别癌症亚型的敏感性较低。 CNN表现出固有的归纳偏差,并且对于图像中感兴趣对象的平移、旋转和位置有所不同。因此,…...
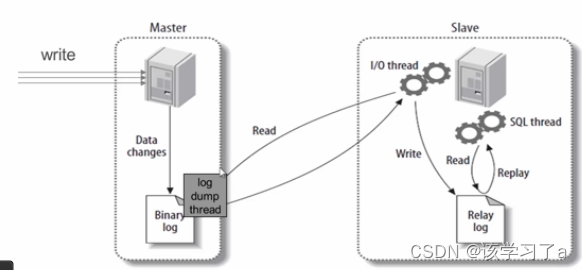
MySQL主从的介绍与应用
mysql主从 文章目录 mysql主从1. 主从简介1.1 主从作用1.2 主从形式 2. 主从复制原理3. 主从复制配置3.1 mysql安装(两台主机安装一致,下面只演示一台主机操作)3.2 mysql主从配置3.2.1 确保从数据库与主数据库里的数据一样3.2.2 在主数据库里…...

pytest中文使用文档----12缓存:记录执行的状态
1. cacheprovider插件 1.1. --lf, --last-failed:只执行上一轮失败的用例1.2. --ff, --failed-first:先执行上一轮失败的用例,再执行其它的1.3. --nf, --new-first:先执行新加的或修改的用例,再执行其它的1.4. --cache…...
【代码随想录】哈希表
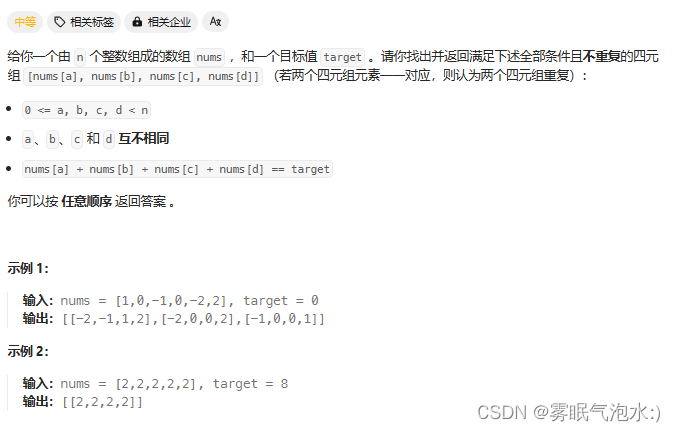
文章目录 242.有效的字母异位词349. 两个数组的交集202. 快乐数1. 两数之和454. 四数相加 II383. 赎金信15. 三数之和18. 四数之和 242.有效的字母异位词 class Solution {public boolean isAnagram(String s, String t) {if(snull || tnull || s.length()!t.length()){return …...

绘图工具 draw.io / diagrams.net 免费在线图表编辑器
拓展阅读 常见免费开源绘图工具 OmniGraffle 创建精确、美观图形的工具 UML-架构图入门介绍 starUML UML 绘制工具 starUML 入门介绍 PlantUML 是绘制 uml 的一个开源项目 UML 等常见图绘制工具 绘图工具 draw.io / diagrams.net 免费在线图表编辑器 绘图工具 excalidr…...

【Vue】 Vue项目中的跨域配置指南
她坐红帐 面带浓妆 唢呐一声唱 明月光 这女子泪眼拜高堂 一拜天地日月 二拜就遗忘这一生 跪三拜红尘凉 庭院 大门锁上 杂乱的眼光 多喧嚷 这女子笑颜几惆怅 余生喜乐悲欢都无关 她眼中已无光 🎵 倪莫问《三拜红尘凉》 在前后端分离的项目开发中…...

跨站脚本攻击XSS
漏洞产生原因: XSS攻击本质上是一种注入攻击,产生原因是Web应用对外部输入参数处理不当,攻击者将恶意代码注入当前Web界面,在用户访问时执行 漏洞攻击手段: 反射型(非持久型)XSS-将payload包…...

C++中的vector与C语言中的数组的区别
C中的vector和C语言中的数组在很多方面都有所不同,以下是它们之间的一些主要区别: 大小可变性: vector是C标准模板库(STL)提供的动态数组容器,它的大小可以动态增长或减少。这意味着你可以在运行时添加或删…...
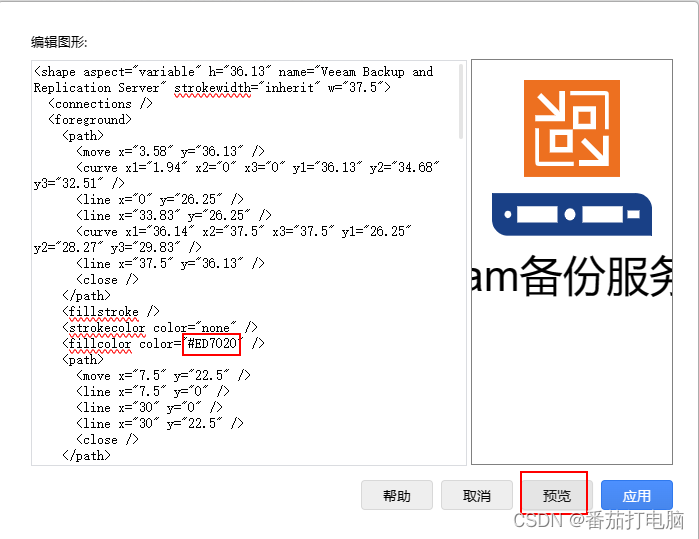
drawio画图编辑图形颜色
drawio画图编辑图形颜色 团队的安全第一图表。将您的存储空间带到我们的在线工具中,或使用桌面应用程序进行本地保存。 1.安装准备 1.1安装平台 多平台 1.2在线使用 浏览器打开网页使用 1.3软件下载 drawio官网github仓库下载 2.在浏览器的网页中使用drawio…...
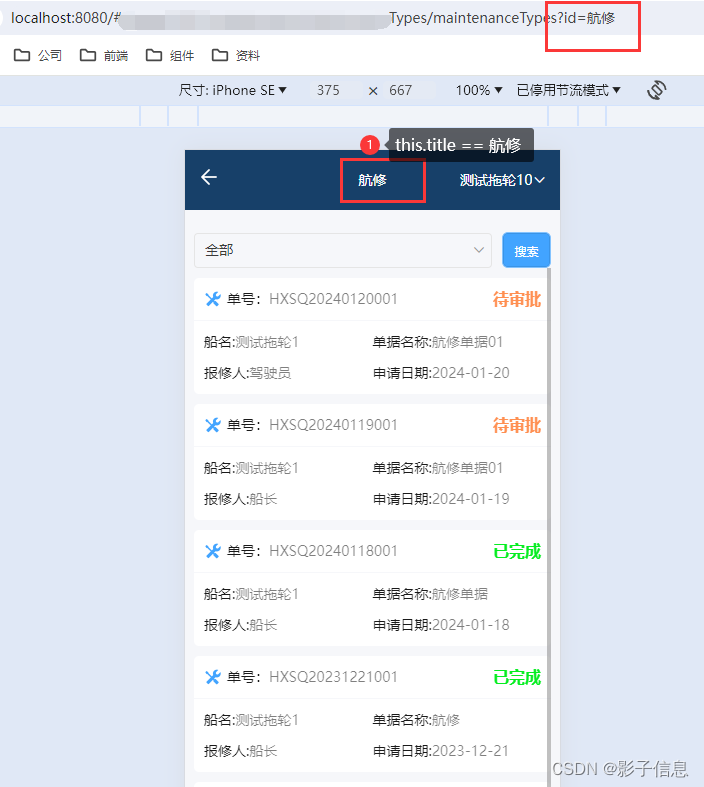
uniapp中uni.navigateTo传递变量
效果展示: 核心代码: uniapp中uni.navigateTo传递变量 methods: {changePages(item) {setDatas("maintenanceFunName", JSON.stringify(item)).then((res) > {uni.navigateTo({url: /pages/PMS/maintenance/maintenanceTypes/maintenanceT…...

Spring Boot 构建war 部署到tomcat下无法在Nacos中注册服务
Spring Boot 构建war 部署到tomcat下无法在Nacos中注册服务 1. 问题2. 分析3. 解决方案参考 1. 问题 使用Nacos作为注册中心的Spring Boot项目,以war包形式部署到服务器上,启动项目发现该服务无法在Nacos中注册。 2. 分析 SpringCloud 项目打 war 包部…...

(2024,Attention-Mamba,MoE 替换 MLP)Jamba:混合 Transformer-Mamba 语言模型
Jamba: A Hybrid Transformer-Mamba Language Model 公和众和号:EDPJ(进 Q 交流群:922230617 或加 VX:CV_EDPJ 进 V 交流群) 目录 0. 摘要 1. 简介 2. 模型架构 3. 收获的好处 3.1 单个 80GB GPU 的 Jamba 实现 …...

“Java泛型” 得所憩,落日美酒聊共挥
本篇会加入个人的所谓鱼式疯言 ❤️❤️❤️鱼式疯言:❤️❤️❤️此疯言非彼疯言 而是理解过并总结出来通俗易懂的大白话, 小编会尽可能的在每个概念后插入鱼式疯言,帮助大家理解的. 🤭🤭🤭可能说的不是那么严谨.但小编初心是能让更多人能接…...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

蓝桥杯 冶炼金属
原题目链接 🔧 冶炼金属转换率推测题解 📜 原题描述 小蓝有一个神奇的炉子用于将普通金属 O O O 冶炼成为一种特殊金属 X X X。这个炉子有一个属性叫转换率 V V V,是一个正整数,表示每 V V V 个普通金属 O O O 可以冶炼出 …...

【1】跨越技术栈鸿沟:字节跳动开源TRAE AI编程IDE的实战体验
2024年初,人工智能编程工具领域发生了一次静默的变革。当字节跳动宣布退出其TRAE项目(一款融合大型语言模型能力的云端AI编程IDE)时,技术社区曾短暂叹息。然而这一退场并非终点——通过开源社区的接力,TRAE在WayToAGI等…...

OpenGL-什么是软OpenGL/软渲染/软光栅?
软OpenGL(Software OpenGL)或者软渲染指完全通过CPU模拟实现的OpenGL渲染方式(包括几何处理、光栅化、着色等),不依赖GPU硬件加速。这种模式通常性能较低,但兼容性极强,常用于不支持硬件加速…...

比较数据迁移后MySQL数据库和ClickHouse数据仓库中的表
设计一个MySQL数据库和Clickhouse数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

Unity基础-Mathf相关
Unity基础-Mathf相关 一、Mathf数学工具 概述 Mathf是Unity中封装好用于数学计算的工具结构体,提供了丰富的数学计算方法,特别适用于游戏开发场景。它是Unity开发中最常用的数学工具之一,能够帮助我们处理各种数学计算和插值运算。 Mathf…...

(33)课54:3 张表的 join-on 连接举例,多表查询总结。数据库编程补述及游标综合例题。静态 sqL与动态sqL(可带参数)
(112)3 张表的 join-on 连接举例 : (113) 多表查询总结 : (114)数据库编程补述 : 综合例题 : 以上没有动手练习,不知道这样的语法是否…...

Github 2025-06-07 Rust开源项目日报Top10
根据Github Trendings的统计,今日(2025-06-07统计)共有10个项目上榜。根据开发语言中项目的数量,汇总情况如下: 开发语言项目数量Rust项目10Dart项目1TypeScript项目1RustDesk: 用Rust编写的开源远程桌面软件 创建周期:1218 天开发语言:Rust, Dart协议类型:GNU Affero Ge…...
