数据结构—二叉树、完全二叉树的性质
# 1
若一棵度为4的树中度为1、2、3、4的结点个数分别为4、3、2、2,则该树的总结点个数是多少?
正确答案:
答案:结点总数n=n0+n1+n2+n3+n4,又由于除根结点外,每个结点都对应一个分支,所以总的分支数等于n-1。而度为i(0≤i≤4)的结点的分支数为i,所以有:总分支数=n-1=0×n0+1×n1+2×n2+3×n3+4×n4。综合两式得:n0=n2+2n3+3n4+1=3+2×2+3×2=14,则n=n0+n1+n2+n3+n4=14+4+3+2+2=25,所以该树的总结点个数是25。
我的答案:
由树的性质,树的总结点个数为树的总度数+1
所以总结点个数为8+6+6+4+1 = 25
# 2
若一棵度为4的树中度为2、3、4的结点个数分别为3、2、2,总结点个数为25,则该树中度为1的结点个数是多少?
正确答案:
答案:结点总数n=n0+n1+n2+n3+n4,又由于除根结点外,每个结点都对应一个分支,所以总的分支数等于n-1。而度为i(0≤i≤4)的结点的分支数为i,所以有:总分支数=n-1=0×n0+1×n1+2×n2+3×n3+4×n4。综合两式得:n0=n2+2n3+3n4+1=3+2×2+3×2=14,则n=n0+n1+n2+n3+n4,n1=n-n0-n2-n3-n4=25-14-3-2-2=4,所以该树中度为1的结点个数是4。
我的答案:
设度为1的结点个数为x
由树的性质总结点个数等于总度数+1得方程2 x+2*3+3*2+4*2 +1= 25
解得x = 4
所以度为1的结点个数是4
# 3
对于度为m的树T,其高度为h,则最少的结点个数和最多的结点个数分别是多少?
正确答案:
答案:第i层最多有mi-1个结点,所以最多结点个数=1+m+m2+…+mh-1=(mh-1)/(m-1)。
最少结点的情况是:某一层有m个结点,其他每层只有一个结点,此时结点个数=m+(h-1)=m+h-1。
我的答案:
最少有m+h-1个
最多有(m^h-1)/(m-1)个
4
对于含有n个结点的m次树,采用孩子链存储结构时,其中空指针域的个数有多少?
正确答案:
答案:该m次树中有n个结点,采用孩子链存储结构时,每个结点有m个指针,总指针域个数=m×n。又由于分支数=n-1,而每个分支是由一个非空指针域引出的,所以总的非空指针域个数=n-1,因此,空指针域的个数=总指针域个数-空指针域的个数=m×n-(n-1)=n(m-1)+1。
我的答案:
对于m次树,它的非空指针域就等于它的边数等于结点个数-1,所以非空指针域有 n-1个
总的指针域有nm个
所以空指针域 = 总指针域 - 非空指针域
空指针域的个数有 nm - (n-1) = n(m-1)+1
# 5
任意一个有n个结点的二叉树,已知它有m个叶子结点,试证明有(n-2m+1)个度数为1的结点。
正确答案:
答案:
证明:设n1为二叉树中度为1的结点数,n2为度2的结点数,则总的结点数为:
n=n1+n2+m
根据二叉树的性质1可知n0=n2+1,即n2=n0-1=m-1,所以有n=n1+n2+m=n1+2m-1,则n1=n-2m+1。
我的答案:
度数之和等于分支数
因为在二叉树中 :
度数之和 = n1 + 2n2
n0 = n2 + 1
分支数 = n - 1
n = n0 + n1 + n2
所以 n0 = m = n2 + 1
所以n1 = n- m- n2 = n - m + 1 = n - 2m +1
# 6
为什么说一棵非空完全二叉树,仅已知叶子结点个数n0,其树形是不能确定的。
正确答案:
答案:
由完全二叉树的特性可知,一旦结点个数n确定了,其树形也就确定了。当只有n0已知时,n2=n0-1,n=n0+n1+n2=2n0-1+n1,而n1可以为0或1,也就是说,n=2n0-1或n=2n0,其结点总数不确定,所以该完全二叉树的形态是不能确定的。
我的答案:
因为如果对于只有一个结点和有两个结点的完全二叉树来说,这两棵树都只有一个叶子结点,即n0 = 1,但树形不一样,所以,对于一棵非空完全二叉树,仅已知叶子结点数n0,树形是不确定的
相关文章:

数据结构—二叉树、完全二叉树的性质
# 1 若一棵度为4的树中度为1、2、3、4的结点个数分别为4、3、2、2,则该树的总结点个数是多少? 正确答案: 答案:结点总数nn0n1n2n3n4,又由于除根结点外,每个结点都对应一个分支,所以总的分支数等…...
JDBC编程复习
文章目录JDBC1.概念2.原理3. 如何使用JDBC编程1. 下载mysql的jdbc驱动2. 项目中引入驱动4. JDBC使用1. 和数据库建立连接2.获取连接3. Statement对象4. 释放资源JDBC 1.概念 JDBC,即Java Database Connectivity,java数据库连接。是Java提供的API用来执行SQL语句&a…...
c++基础入门二
一、数组的引用int main() {int a 10, b 20;int ar[10] { 1,2,3,4,6,7 };int& x ar[0];int& p[5] ar;//errorint(&p)[10] ar;//引用整个数组的大小sizeof(ar)int(*p)[10] &ar;//typesize表示整个数组//只有在这三种情况下代表整个数组,其他情…...
企业数字化转型的产品设计思路
数字化转型的核心是全面重塑企业的管理模式和经营模式,是迈向数字经济时代的方式。一、到底什么是数字化转型?数字化转型并不神秘。数字化转型是一种经营方式、一种经营理念,是将企业相关的人、物料、设备、资金等要素进行系统运转࿰…...

Linux日志分析常用命令
一:常用命令1、tail参数: tail [ -f ] [ -c Number | -n Number | -m Number | -b Number | -k Number ] [ File ] 参数说明: -f 该参数用于监视File文件增长。 -c Number 从 Number 字节位置读取指定文件 -n Number 从 Number 行位置读取指…...
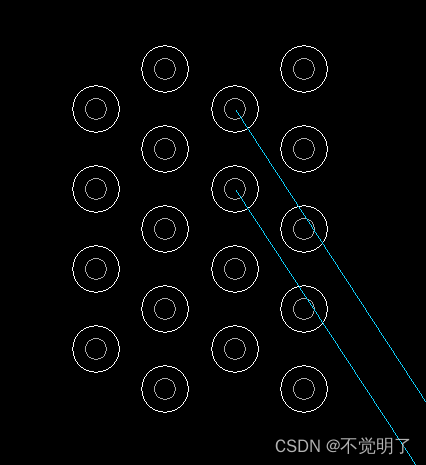
Allegro如何使用Snake命令走蛇形线操作指导
Allegro如何使用Snake命令走蛇形线操作指导 在做PCB设计的时候,遇到不规则BGA的时候,蛇形走线是惯用的走线方式,类似下图 Allegro支持蛇形走线,具体操作如下 首先把过孔打好,尽量上下左右间距一致,不容易出现偏差,如下图在Command命令栏下方输入snake,然后回车...

在 Eclipse 中创建 Maven 项目
1.在 Eclipse 中配置 MavenEclipse 中默认自带 Maven 插件,但是自带的 Maven 插件不能修改本地仓库,所以通常我们不使用自带的 Maven ,而是使用自己安装的,在 Eclipse 中配置 Maven 的步骤如下: 1) 点击 Eclipse 中的 …...

flex 布局相关属性的使用
简单概述 为元素添加 display:flex; 的属性后,当前元素被视为弹性布局的盒子容器(box),其子元素被视为弹性布局项目(item)。item 会在 box 内灵活布局,解决了对齐、分布、尺寸等响应式问题。 演示 demo <template><div class&quo…...

【C++】类和对象(第一篇)
文章目录1. 面向过程和面向对象初步认识2.类的引入3.类的定义3.1 类的两种定义方式3.2 成员变量命名规则建议4. 类的访问限定符及封装4.1 访问限定符4.2 封装5. 类的作用域6. 类的实例化7. 类对象模型7.1 类对象大小的计算7.2 类对象的存储方式猜测7.3 结构体内存对齐规则复习8…...

springboot 接入websocket实现定时推送消息到客户端
目录说明代码实现说明 如标题,举例需求场景: 前端与后端websocket连接上后,多用户登录,后端根据不同用户定时发消息给前端用于展示 代码实现 1、 <dependency><groupId>org.springframework.boot</groupId>…...
虚拟机磁盘重新分区增加Docker磁盘空间
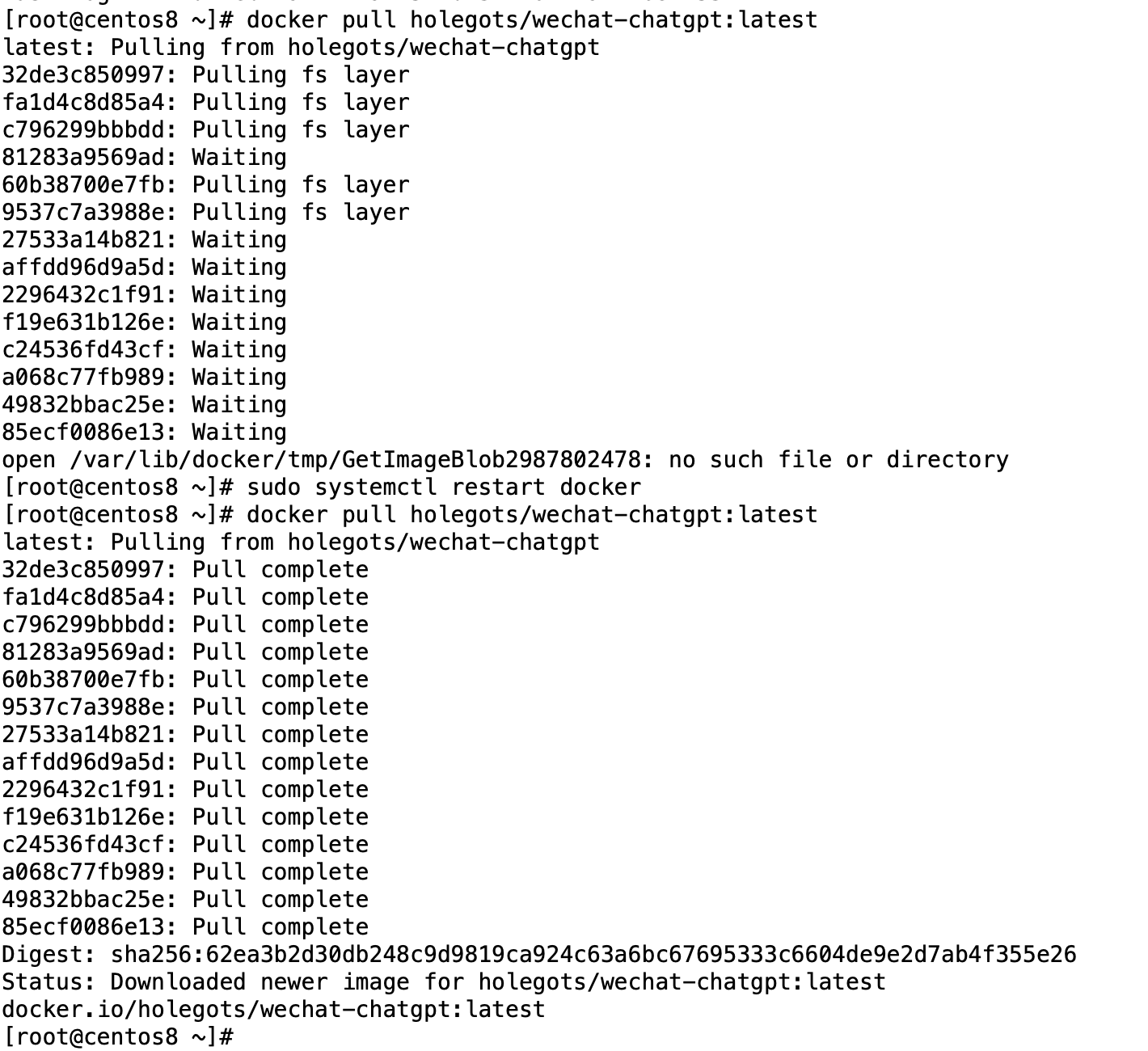
目录一、简介二、重新分区 挂载目录2.1 增加虚拟机硬盘空间2.2 重新分区2.3 格式化新分区2.4 挂载docker目录三、重新拉取一、简介 今天在使用docker pull 拉取镜像时,报了no such file or directory的信息,原来是Docker的磁盘空间满了 #查看Docker Roo…...
Java开发学习(四十八)----MyBatisPlus删除语句之逻辑删除
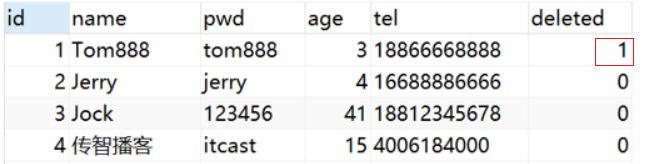
1、逻辑删除 接下来要讲解是删除中比较重要的一个操作,逻辑删除,先来分析下问题: 这是一个员工和其所签的合同表,关系是一个员工可以签多个合同,是一个一(员工)对多(合同)的表 员工ID为1的张业绩,总共签了三个合同&a…...
RabbitMq
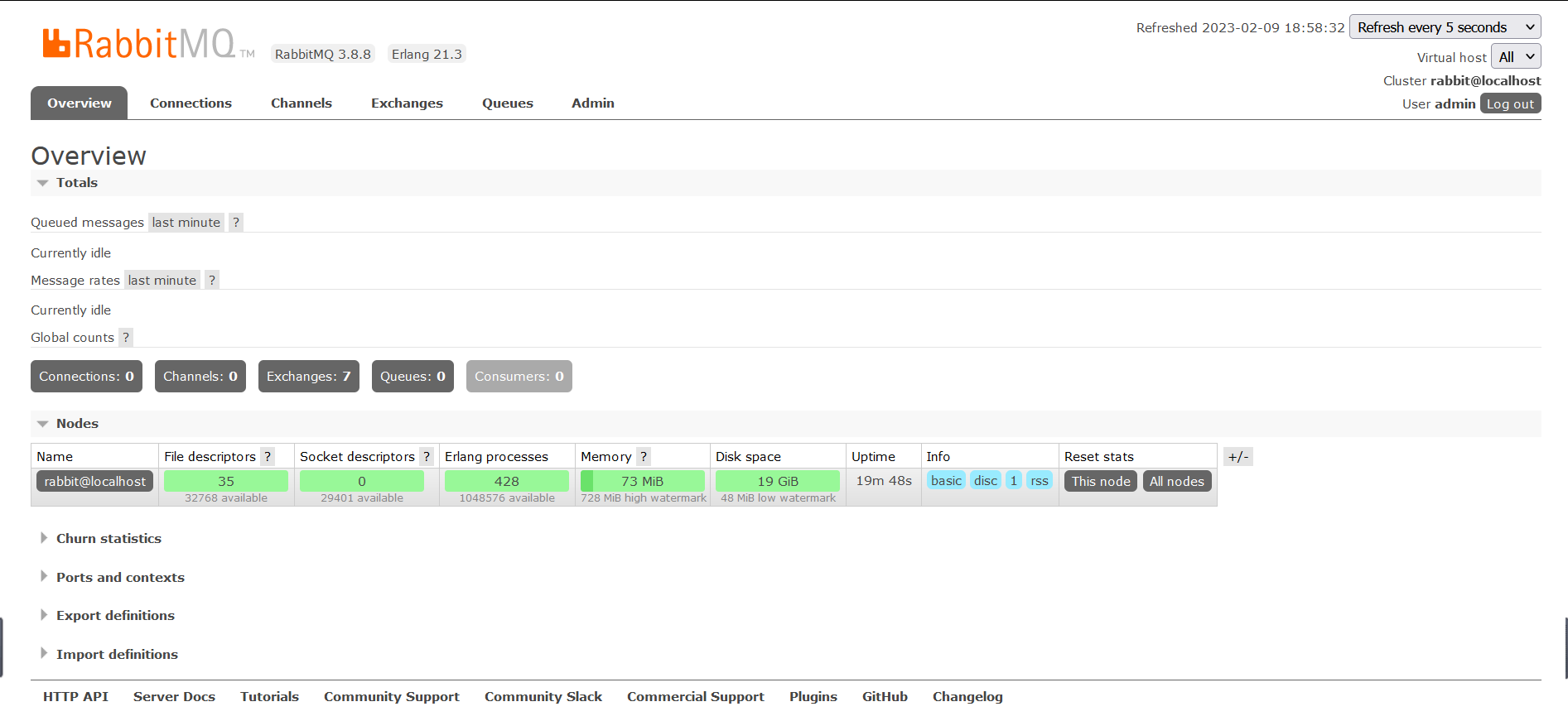
一、四大核心概念生产者:产生数据发送消息的程序是生产者交换机:交换机是RabbitMQ非常重要的一个部件,一方面它接收来自生产者的消息,另一方面它将消息推送到队列中。交换机必须确切知道如何处理它接收到的消息,是将这…...
Qt学习笔记
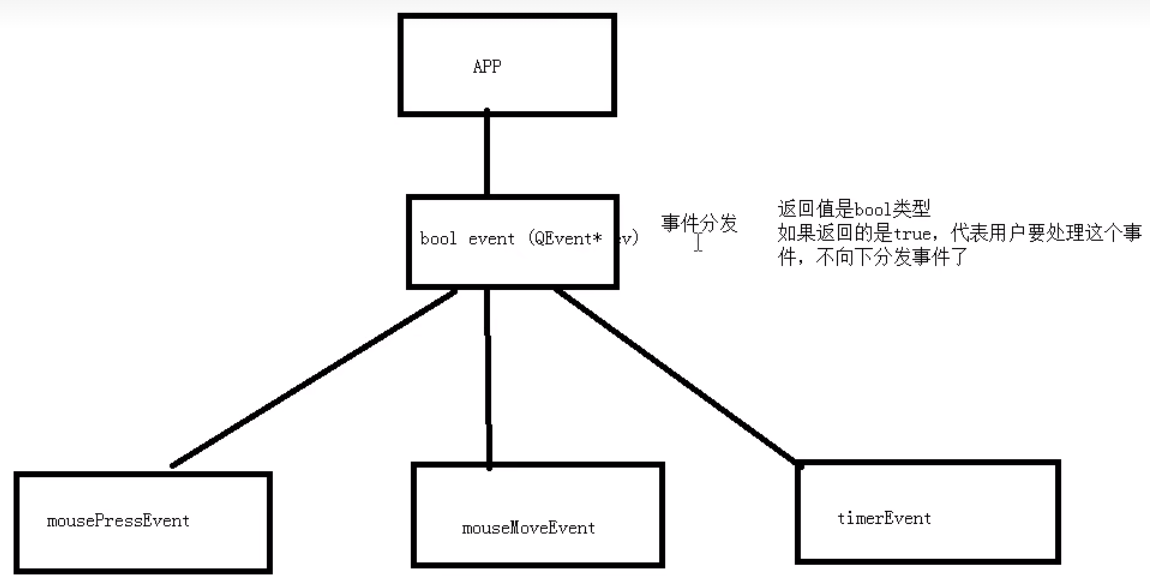
文章目录一、C指针函数驼峰命名法、下划线命名法编程报错二、C三、Qt语法Qt历史、Qt应用Qt特色快捷键Qt类的族谱QWidgetQPushButtonQDebug对象树Qt窗口坐标信号和槽Qt自带的信号的槽自定义的信号和槽Qt4版本 vs Qt5版本 的connect写法函数指针解决重载问题拓展类型转换QString …...
洛谷——P1091 合唱队形
【题目描述】 n 位同学站成一排,音乐老师要请其中的 n−k 位同学出列,使得剩下的 k 位同学排成合唱队形。 合唱队形是指这样的一种队形:设 kk 位同学从左到右依次编号为 1,2, … ,k,他们的身高分别为,, … ,,则…...
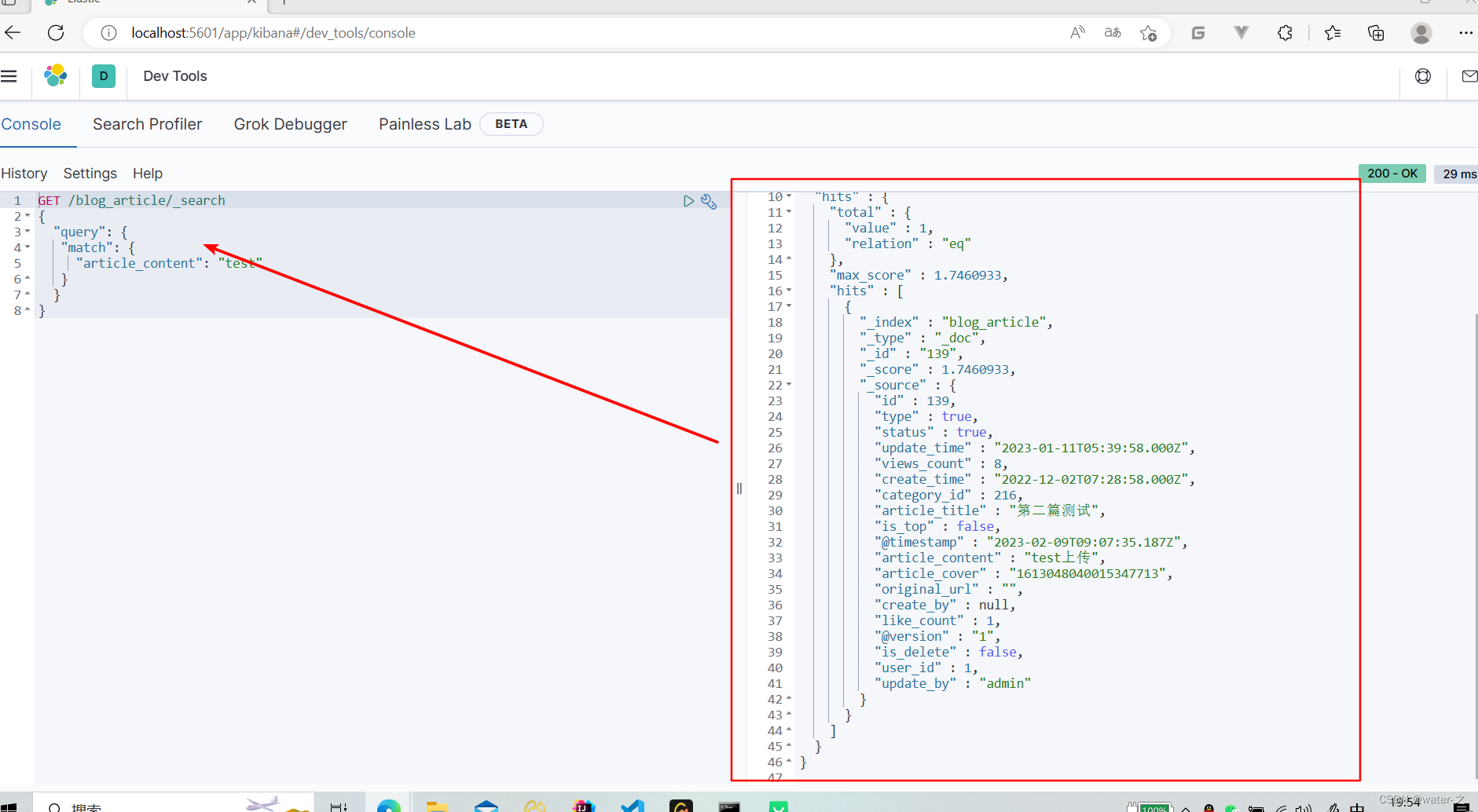
使用logstash把mysql同步到es,Kibana可视化查看
1:首先需要电脑本地有es环境,并且要牢记版本后,后续安装的logstash和Kibana一定要版本对应 查看es版本:http://localhost:9200/ 2:安装对应版本的logstash:找到自己对应ES版本,然后解压 Logst…...

Vue3.0 setup的使用及作用
目录开篇:1.什么是setup2.setup怎么使用3.setup中包含的生命周期函数3.setup相关参数4.setup特性总结总结开篇: 从vue2升级 vue3,vue3是可以兼容vue2。所以v3可以采用v2的选项式api,但是v2不能使用v3的组合式api,由于…...

Ubuntu18.04安装Vertica
目录下载安装包安装(Ubuntu18.04)配置 I/O Scheduler配置 TZSupport Tools配置 swapinessDisk ReadaheadEnabling chrony or ntpd自启动项错误处理后重装下载安装包 官网11.0版本或者10.0(deb)安装包可私信提供百度网盘链接; 安装(Ubuntu18.04) testvertica:~$ s…...
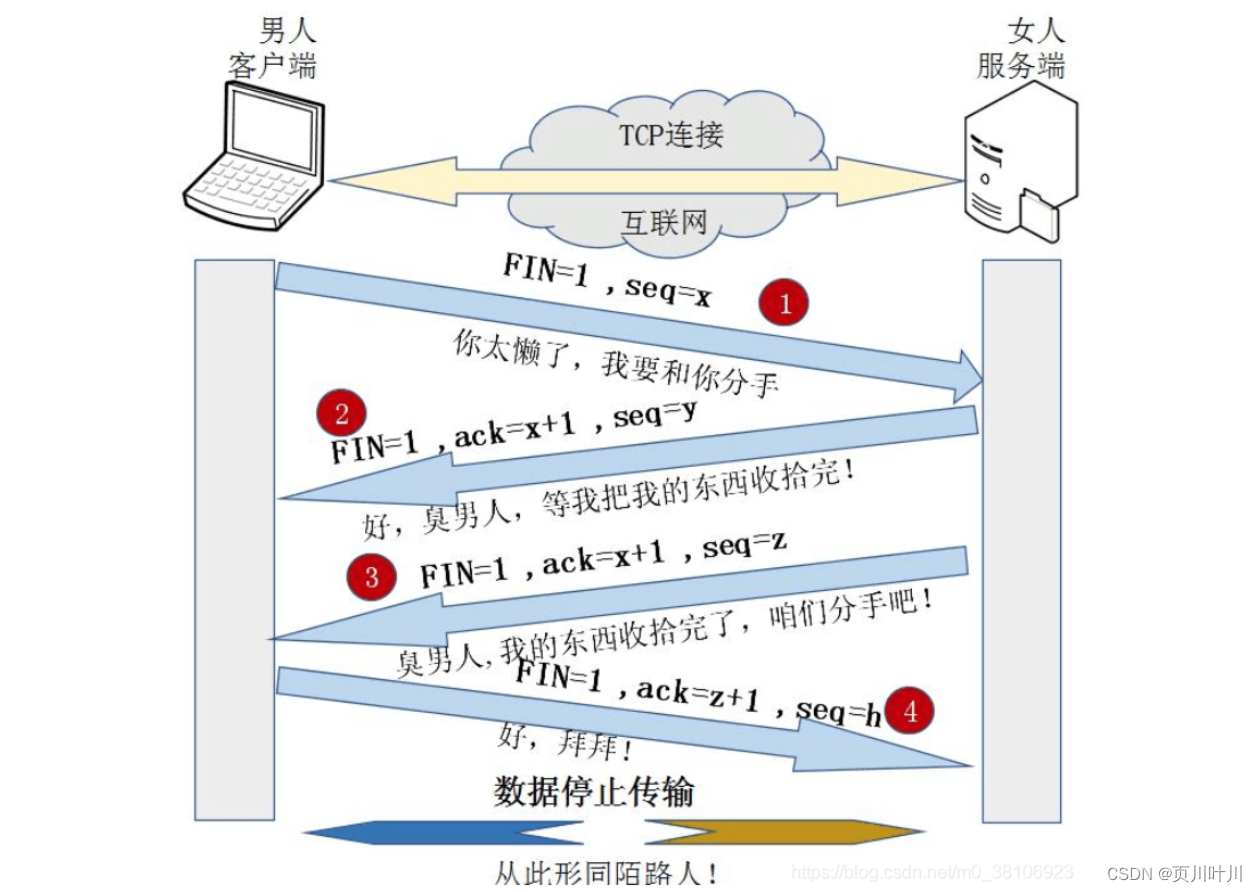
2.计算机基础-计算机网络面试题—基础知识、容器、面向对象、并发编程
本文目录如下:计算机基础-计算机网络 面试题一、基础知识简述 TCP 和 UDP 的区别?http与https的区别?Session 和 Cookie 有什么区别?URL是什么?由哪些部分组成?OSI 的 五层模型 都有哪些?get 和 post 请求…...
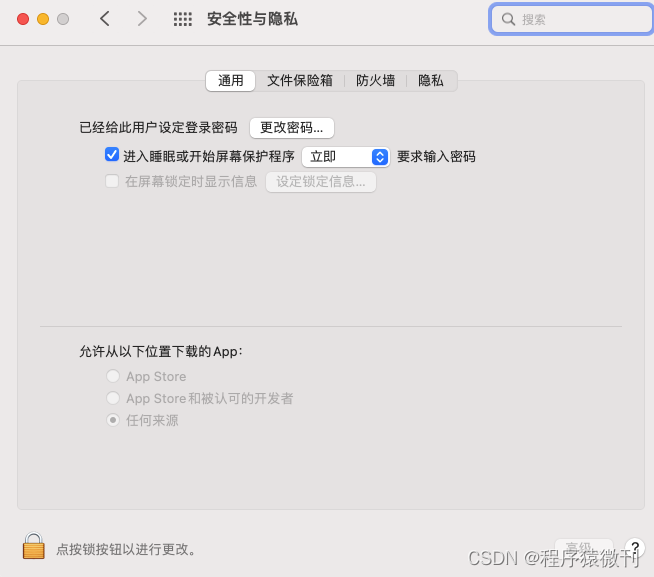
解决Mac 安装应用提示:xx已损坏,无法打开。 您应该将它移到废纸篓问题
许多新手mac 用户安装应用得时候会出现 “已损坏,无法打开。您应该将它移到废纸娄” 导致无法正常安装,其实应用软件b并没有损坏,只是系统安全设置,我们改如何解决呢? 1、开启允许任何来源 苹果已经取消了允许“任何…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

eNSP-Cloud(实现本地电脑与eNSP内设备之间通信)
说明: 想象一下,你正在用eNSP搭建一个虚拟的网络世界,里面有虚拟的路由器、交换机、电脑(PC)等等。这些设备都在你的电脑里面“运行”,它们之间可以互相通信,就像一个封闭的小王国。 但是&#…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

CocosCreator 之 JavaScript/TypeScript和Java的相互交互
引擎版本: 3.8.1 语言: JavaScript/TypeScript、C、Java 环境:Window 参考:Java原生反射机制 您好,我是鹤九日! 回顾 在上篇文章中:CocosCreator Android项目接入UnityAds 广告SDK。 我们简单讲…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

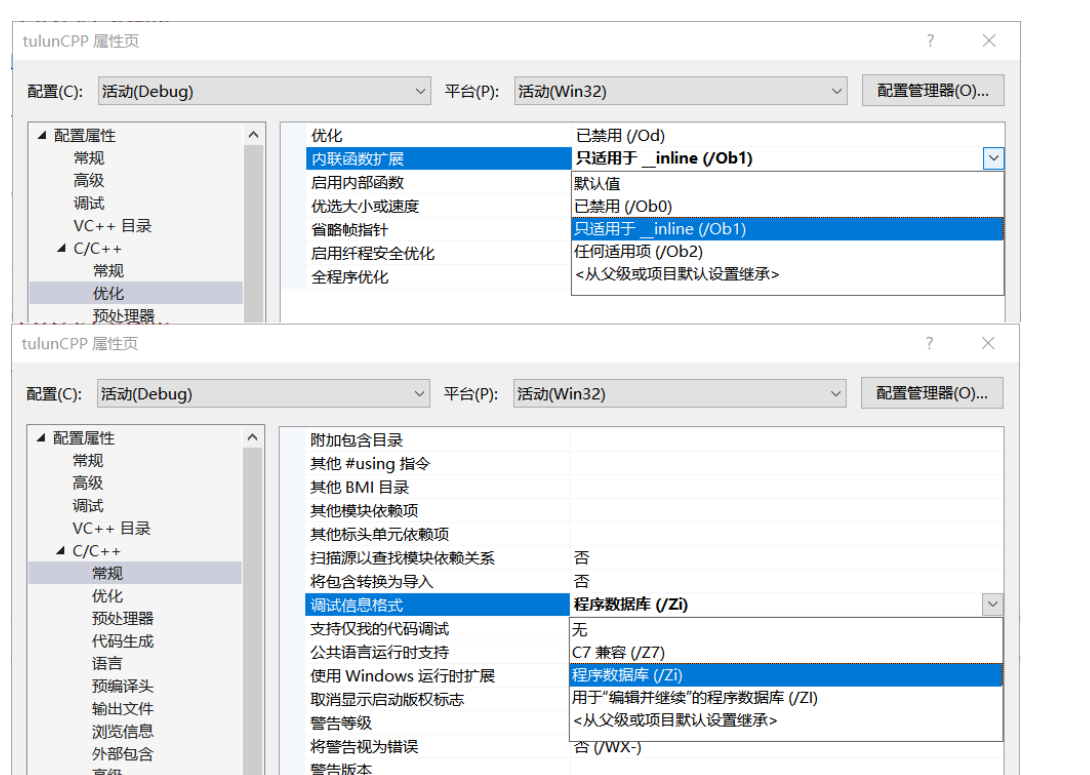
CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

实战三:开发网页端界面完成黑白视频转为彩色视频
一、需求描述 设计一个简单的视频上色应用,用户可以通过网页界面上传黑白视频,系统会自动将其转换为彩色视频。整个过程对用户来说非常简单直观,不需要了解技术细节。 效果图 二、实现思路 总体思路: 用户通过Gradio界面上…...
