【刷题】-- 基础 -- 二分查找
精于结构、敏于心智、熟于代码
方式:对于会的代码:学会以最快的速度构建,并以最快的速度书写;对于不会的代码:学会(以最短的路径下)看懂别人的代码。学会使用参考文档、熟悉每一个容器。
刷题位置:「算法」 - 学习计划 - 力扣(LeetCode)全球极客挚爱的技术成长平台
对于二分查找问题的基础解决思路:(特点:遍历都可以进行解决 -> 问题:时间复杂度相较于过大)
- 查找的过程,本质就是排除的过程。(一次排除一批)
- 抓紧题目所给的关键特点。(排列方式,查询特点)
- 以while循环查找 -> 找到了 / 确定查找范围的边界。(循环结束的条件)
704. 二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9输出: 4
解释: 9 出现在nums中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2输出: -1
解释: 2 不存在 nums 中因此返回 -1
针对于本题:
关键点:我们需要在一个升序的数组中找到一个值是否存在。
核心:
- 可以通过左小右大进行,中间位置的log2的缩小范围。
- left的范围跟新为 mid + 1,right的范围跟新为 mid + 1。
- 整个范围找完即 left > right 此时无该值。
特殊点:
- 只有一个值的时候 / right 更新 (mid - 1) == left,恰好值是left位置,对left同理 -> while循环增加一个left = right是至关重要的。
- 防止数组大小为空(此题说了size >= 1,此处就没事)。
- 最好别写为mid = (right + left) / 2,因为有 (right + left) 会导致数据过大。
class Solution {
public:int search(vector<int>& nums, int target) {// 保证比较的位置是有效数据段中的中间位置int left = 0, right = nums.size() - 1;int mid = right / 2;//if(nums.empty())// return -1;// 左的下标大于右,即有效数据段比完了:left < right// 防止出现只有一个数据、如right = mid + 1 == left -> nums[left] == target的时候。while(left <= right){// 移动左右下标到有效区域if(nums[mid] < target)left = mid + 1;else if(nums[mid] > target)right = mid - 1;elsereturn mid;mid = left + (right - left) / 2;}return -1;}
};复杂度分析
-
时间复杂度:O(logn),其中 n 是数组的长度。
-
空间复杂度:O(1)。
类似题
374.猜数字大小
猜数字游戏的规则如下:
每轮游戏,我都会从 1 到 n 随机选择一个数字。 请你猜选出的是哪个数字。如果你猜错了,我会告诉你,你猜测的数字比我选出的数字是大了还是小了。你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果,返回值一共有 3 种可能的情况(-1,1 或 0):
-1:我选出的数字比你猜的数字小 pick < num。
1:我选出的数字比你猜的数字大 pick > num。0:我选出的数字和你猜的数字一样。恭喜!你猜对了!pick == num。
返回我选出的数字。
/** * Forward declaration of guess API.* @param num your guess* @return -1 if num is higher than the picked number* 1 if num is lower than the picked number* otherwise return 0* int guess(int num);*/class Solution {
public:int guessNumber(int n) {int left = 1, right = n;int mid = left + (right - left) / 2;while(left <= right){if(guess(mid) == 0)return mid;else if(guess(mid) == 1)left = mid + 1;elseright = mid - 1;mid = left + (right - left) / 2;}return -1;}
};278.第一个错误的版本
你是产品经理,目前正在带领一个团队开发新的产品。不幸的是,你的产品的最新版本没有通过质量检测。由于每个版本都是基于之前的版本开发的,所以错误的版本之后的所有版本都是错的。
假设你有 n 个版本 [1, 2, ..., n],你想找出导致之后所有版本出错的第一个错误的版本。
你可以通过调用 bool isBadVersion(version) 接口来判断版本号 version 是否在单元测试中出错。实现一个函数来查找第一个错误的版本。你应该尽量减少对调用 API 的次数。
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);class Solution {
public:int firstBadVersion(int n) {uint64_t left = 1, right = n;uint64_t mid = (right + left) / 2;while(left <= right){if(!isBadVersion(mid) && !isBadVersion(mid + 1)){left = mid + 1;else if(isBadVersion(mid) && isBadVersion(mid - 1))right = mid - 1;elseif(isBadVersion(mid))return mid;elsereturn mid + 1;mid = left + (right - left) / 2;}return -1;}
};按照常见二分查找的书写,上面的题肯定是可以对的,但是有点过于的臃肿,效率是够的,但是对于程序员是不友好的,所以我们可以进行优化一下。
特殊点:
此处由于我们需要第一个 bool isBadVersion(version) 为对的, 所以对与right我们可以right = mid,因为我们无法确定它是不是第一个,所以我们不能排除掉它。对于left的 bool isBadVersion(version) 为错,不需要,即:left = mid + 1。
一个right = mid,另一个left = mid + 1,则left == right时就找到了。
// The API isBadVersion is defined for you.
// bool isBadVersion(int version);class Solution {
public:int firstBadVersion(int n) {int left = 1, right = n;while(left < right){int mid = left + (right - left) / 2;if(isBadVersion(mid))right = mid;elseleft = mid + 1;}// 此时left == rightreturn left;}
};针对上述的类似写法我们还可以解决一个题。
35.搜索插入的位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
class Solution {
public:int searchInsert(vector<int>& nums, int target) {int left = 0, right = nums.size();while(left < right){int mid = left + (right - left) / 2;if(target < nums[mid])right = mid;elseleft = mid + 1;}// left == rightif(left && nums[left - 1] == target)return left - 1;return left;}
};相关文章:

【刷题】-- 基础 -- 二分查找
精于结构、敏于心智、熟于代码 方式:对于会的代码:学会以最快的速度构建,并以最快的速度书写;对于不会的代码:学会(以最短的路径下)看懂别人的代码。学会使用参考文档、熟悉每一个容器。 刷题位…...

Spark MLlib 特征工程
Spark MLlib 特征工程预处理特征选择归一化离散化Embedding向量计算特征工程制约了模型效果 : 决定了模型效果的上限 , 而模型调优只是在不停地逼近上限好的特征工程才能有好的模型 特征处理函数分类 : 预处理 : 将模型无法直接消费的数据,转为可消费的数据形式特…...

CentOS7 完全卸载 php
在 CentOS 7 使用 yum install 简单安装 php 后,发现 php 版本 5.4 ,太低了! 然后,使用 yum remove 简单卸载后,发现 php 还在,不干净! 只好 rpm 慢慢卸载 rpm -qa |grep php php-gd-5.4.16-4…...

关于OCS认证里必须知晓的内容
【关于OCS认证里必须知晓的内容】美国非营利组织Textile Exchange推出的有机认证标准——有机含量标准(The Organic Content Standard),简称OCS。该标准通过跟踪有机原材料的种植从而监管整个有机产业链。OCS将应用于各种有机种植原料的验证,而不只限于有…...

创业做电商难不难?新人做电商怎么才能挣钱?
这几年经济不景气,创业做电商的人越来越多,但是,对于多数人来说,一开始做电商,都是试错成本,没有系统学习或者是跟着半吊子二把刀学的,结果赔钱就算了,新人创业做电商到底难不难&…...
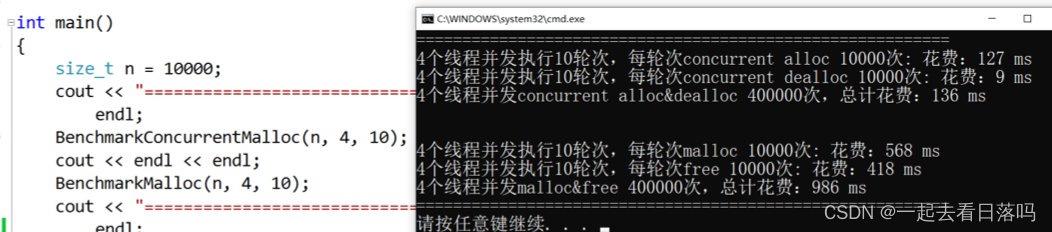
【项目设计】高并发内存池(七)[性能测试和提升]
🎇C学习历程:入门 博客主页:一起去看日落吗持续分享博主的C学习历程博主的能力有限,出现错误希望大家不吝赐教分享给大家一句我很喜欢的话: 也许你现在做的事情,暂时看不到成果,但不要忘记&…...

PHP:Laravel cast array json数据存数据库时unicode 编码问题和update更新不触发数据转换
目录问题描述问题解决方式一:自定义属性方式二:继承覆写方式三:trait复用方式四:定义Cast子类update不生效参考文章问题描述 Model示例 class UserModel extends Model {protected $table tb_user;protected $casts [alias …...
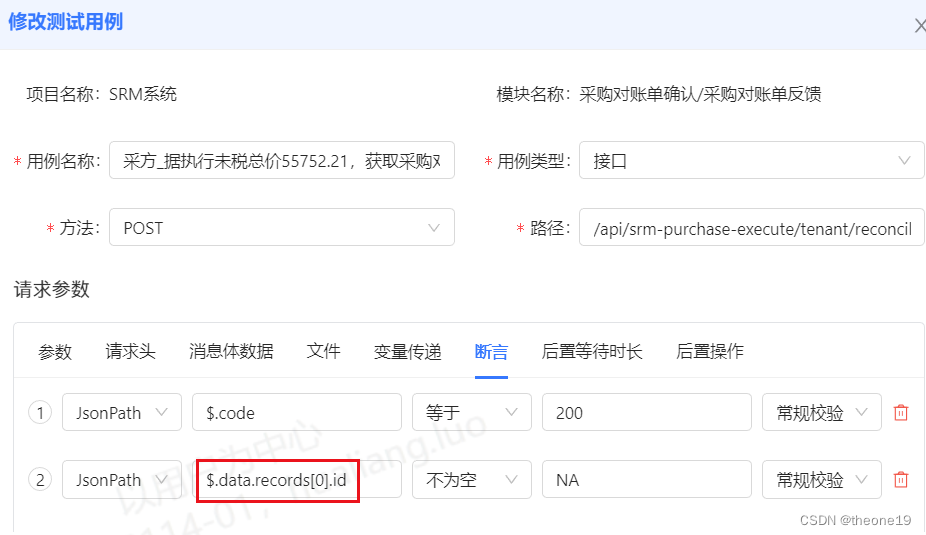
自动化测试总结--断言
采购对账测试业务流程中,其中一个测试步骤总是失败,原因是用例中参数写错及断言不明确 一、问题现象: 采购对账主流程中,其中一个步骤失败了,会导致这个套件一直失败 图(1)测试报告视图中&…...

传输线的物理基础(三):传输线的瞬时阻抗
每个信号都有一个上升时间 RT,通常是从 10% 到 90% 的电压电平测量的。当信号沿传输线向下移动时,前沿在传输线上展开并具有空间范围。如果我们可以冻结时间并观察电压分布向外移动时的大小,我们会发现类似下图的东西。传输线上上升时间的长度…...

第六章:多线程
第六章:多线程 6.1:程序、进程、线程基本概念 程序 程序program是为了完成特定任务、用某种语言编写的一组指令的集合。即指一段静态的代码,静态对象。 进程 进程process是程序的一次执行过程,或是正在运行的一个程序。是一个…...
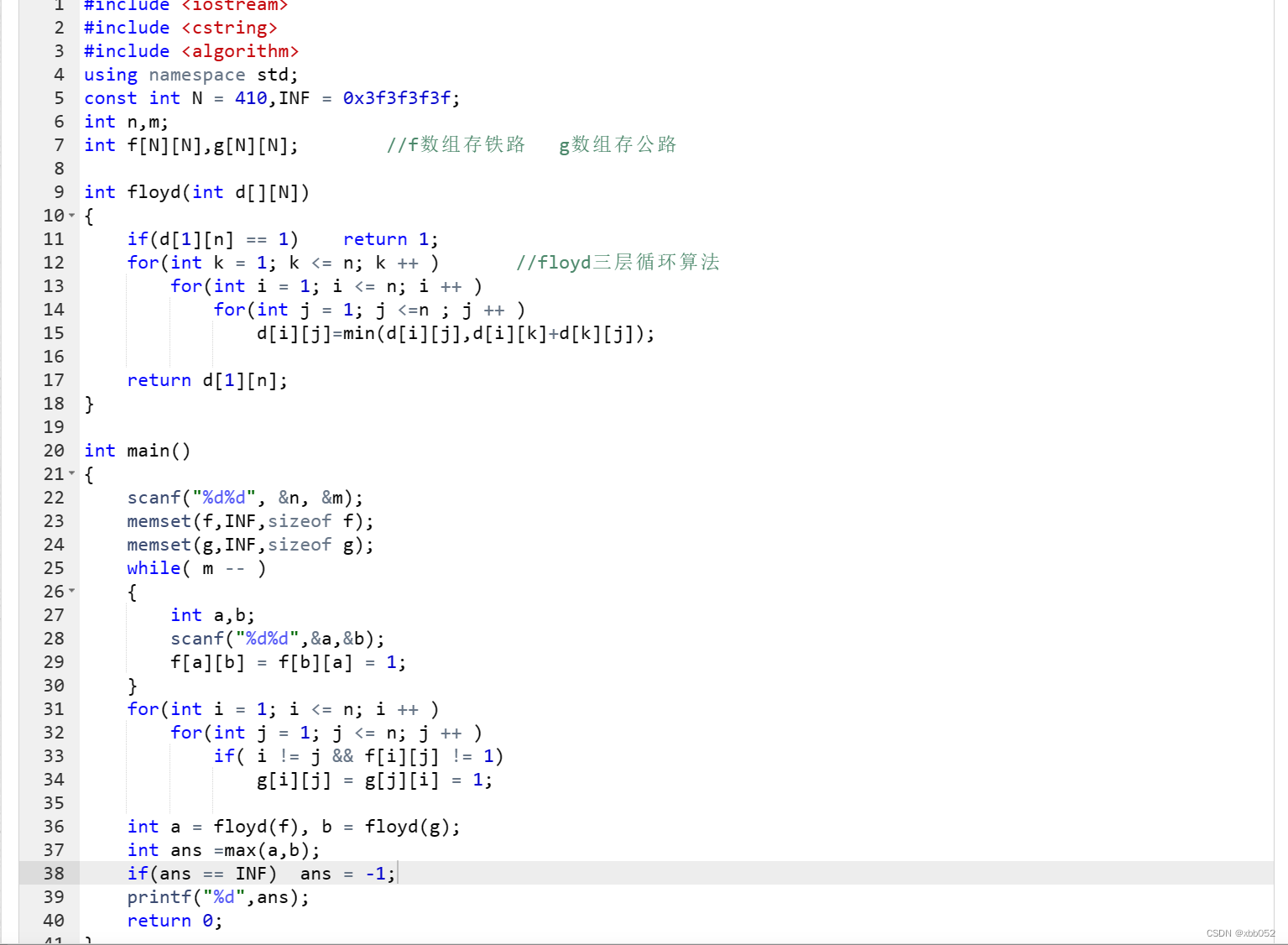
铁路与公路
蓝桥杯集训每日一题acwing4074 某国家有 n 个城市(编号 1∼n)和 m 条双向铁路。 每条铁路连接两个不同的城市,没有两条铁路连接同一对城市。 除了铁路以外,该国家还有公路。 对于每对不同的城市 x,y,当且仅当它们之…...

GitHub Copilot 全新升级,工作效率提升 55%
2021年 6 月,GitHub 和 OpenAI 推出了 GitHub Copilot 预览版,可根据命名或者正在编辑的代码上下文为开发者提供代码建议,被称为“你的 AI 结对程序员”。 近日,GitHub 宣布,经过去年 12 月以来的短暂测试后ÿ…...

【IoT】《天道》中音响案例的SWOT分析
在20世纪80年代初,SWOT最初是由美国知名管理学教授海因茨韦里克提出的。 之后这个工具就经常被用于企业的战略分析、竞争对手分析等场景。 在每年例行的公司产品规划过程中,我个人也经常使用这个工具。 由于涉及一些公司商业上的信息,下面会用…...
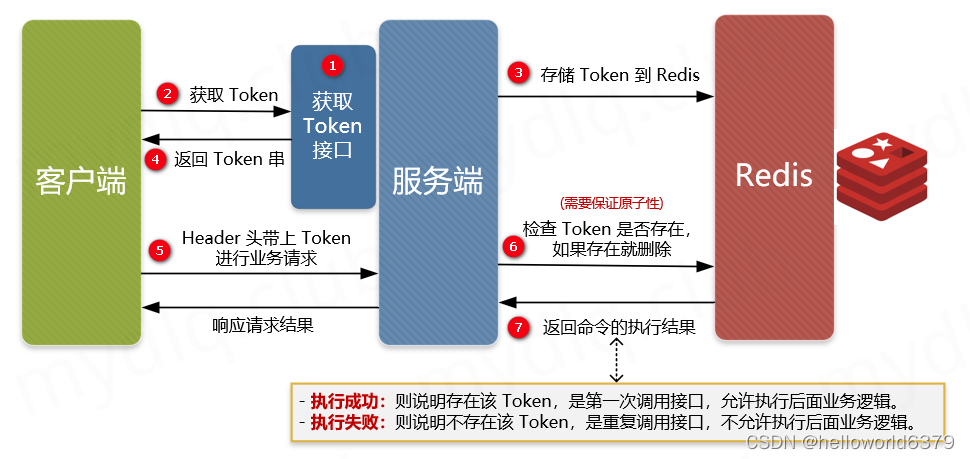
如何实现接口幂等性
1 什么是幂等 幂等操作的特点是一次或者任意多次执行所产生的影响均与一次执行的影响相同,不会因为多次的请求而产生不一样的结果。换句话说,就是我使用相同的请求参数,去请求同一个接口,不管请求多少次获取到的响应数据应该是一…...

相恨见晚的office办公神器(不坑盒子/打工人Excel插件2023年最新版)
不坑盒子 这是一个非常好用的插件工具,专门应用在Word文档和wps,支持Office 2010以上的版本,操作也简单且实用。 不坑盒子下载及使用说明 一键排版功能 像是下面的自动排版功能,可以在配置里面先设定好需要的格式,…...
matlab基础到实战(1)
目录概述sin函数例子四则运算实数复数逻辑运算复数运算模幅角共轭向量二维向量定义序列生成向量向量索引方式加减乘除向量间运算加减乘法除法概述 MATLAB是美国MathWorks公司出品的商业数学软件,用于数据分析、无线通信、深度学习、图像处理与计算机视觉、信号处理…...

谷歌发布编写分布式应用的框架Service Weaver
一个新的框架,在本地以模块化单体的形式运行,一旦部署,则为分布式微服务架构 转载请注明来源:https://janrs.com/2023/03/%e8%b0%b7%e6%ad%8c%e5%8f%91%e5%b8%83%e7%bc%96%e5%86%99%e5%88%86%e5%b8%83%e5%bc%8f%e5%ba%94%e7%94%a8…...
详解FPGA:人工智能时代的驱动引擎观后感
详解FPGA:人工智能时代的驱动引擎观后感 本书大目录 第一章 延续摩尔定律 第二章 拥抱大数据的洪流 第三章 FPGA在人工智能时代的独特优势 第四章 更简单也更复杂——FPGA开发的新方法 第五章 站在巨人肩上——FPGA发展新趋势 文章目录详解FPGA:人工智能…...

Rest/Restful接口
Rest Rest的全称是Representational State Transfer 。Rest是一种架构风格。Rest有很多原则和限制: 客户端-服务端架构模式无状态可缓存统一接口分层系统按需缓存 Rest对我们开发人员来说基本上就是资源,我们一般通过URI表示我们请求的一个资源。例如:…...
【vue init】三.项目引入axios、申明全局变量、设置跨域
教程目录 一:《【vue init】使用vue init搭建vue项目》 二:《【vue init】项目使用vue-router,引入ant-design-vue的UI框架,引入less》 三:《【vue init】项目引入axios、申明全局变量、设置跨域》 根据前文《【vue init】项目使…...

Ubuntu系统下交叉编译openssl
一、参考资料 OpenSSL&&libcurl库的交叉编译 - hesetone - 博客园 二、准备工作 1. 编译环境 宿主机:Ubuntu 20.04.6 LTSHost:ARM32位交叉编译器:arm-linux-gnueabihf-gcc-11.1.0 2. 设置交叉编译工具链 在交叉编译之前&#x…...

C++_核心编程_多态案例二-制作饮品
#include <iostream> #include <string> using namespace std;/*制作饮品的大致流程为:煮水 - 冲泡 - 倒入杯中 - 加入辅料 利用多态技术实现本案例,提供抽象制作饮品基类,提供子类制作咖啡和茶叶*//*基类*/ class AbstractDr…...

《Qt C++ 与 OpenCV:解锁视频播放程序设计的奥秘》
引言:探索视频播放程序设计之旅 在当今数字化时代,多媒体应用已渗透到我们生活的方方面面,从日常的视频娱乐到专业的视频监控、视频会议系统,视频播放程序作为多媒体应用的核心组成部分,扮演着至关重要的角色。无论是在个人电脑、移动设备还是智能电视等平台上,用户都期望…...

从深圳崛起的“机器之眼”:赴港乐动机器人的万亿赛道赶考路
进入2025年以来,尽管围绕人形机器人、具身智能等机器人赛道的质疑声不断,但全球市场热度依然高涨,入局者持续增加。 以国内市场为例,天眼查专业版数据显示,截至5月底,我国现存在业、存续状态的机器人相关企…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Java多线程实现之Callable接口深度解析
Java多线程实现之Callable接口深度解析 一、Callable接口概述1.1 接口定义1.2 与Runnable接口的对比1.3 Future接口与FutureTask类 二、Callable接口的基本使用方法2.1 传统方式实现Callable接口2.2 使用Lambda表达式简化Callable实现2.3 使用FutureTask类执行Callable任务 三、…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...
