如何处理ubuntu22.04LTS安装过程中出现“Daemons using outdated libraries”提示
Ubuntu 22.04 LTS 中使用命令行升级软件或安装任何新软件时,您可能收到“Daemons using outdated libraries”,“Which services should be restarted?”的提示,提示下面列出备选的重启服务,如下。
使用以下命令,能够修复此类问题。
(1)安装 needrestart
默认情况下,needrestart 已经安装在 Ubuntu 中。如果没有,您可以使用以下命令安装。
sudo apt install needrestart
(2)显示所有应重新启动的服务
使用以下命令行显示应重新启动哪些服务。
sudo needrestart -b
(3)检查并重新启动
现在检查并重新启动服务应使用下面编写的命令重新启动。
sudo needrestart -u NeedRestart::UI::stdio -r l
sudo needrestart -u NeedRestart::UI::stdio -r a(4)重启服务器
reboot
(5)确认
重启服务器后,确认重新启动的服务的变化。
sudo needrestart -b
再次确认一下needrestart的状态。
sudo needrestart -u NeedRestart::UI::stdio -r l
如下,即正常。

(6)总结
下表总结了上述使用的命令。
| 命令 | 描述 |
| sudo apt install needrestart | 在 ubuntu 中安装 needrestart 服务 |
| sudo needrestart -b | 以机器可读格式显示需要重新启动的服务内容 |
| sudo needrestart -u NeedRestart::UI::stdio -r l | 以人类可读格式显示需要重新启动的服务内容 |
| sudo needrestart -u NeedRestart::UI::stdio -r a | 重启服务器 |
| reboot | 重启服务器 |
相关文章:

如何处理ubuntu22.04LTS安装过程中出现“Daemons using outdated libraries”提示
Ubuntu 22.04 LTS 中使用命令行升级软件或安装任何新软件时,您可能收到“Daemons using outdated libraries”,“Which services should be restarted?”的提示,提示下面列出备选的重启服务,如下。 使用以下命令,能够…...
跟TED演讲学英文:The inside story of ChatGPT‘s astonishing potential by Greg Brockman
The inside story of ChatGPT’s astonishing potential Link: https://www.ted.com/talks/greg_brockman_the_inside_story_of_chatgpt_s_astonishing_potential Speaker: Greg Brockman Date:April 2023 文章目录 The inside story of ChatGPTs astonishing potentialIntro…...

mybatis05:复杂查询:(多对一,一对多)
mybatis05:复杂查询:(多对一,一对多) 文章目录 mybatis05:复杂查询:(多对一,一对多)前言:多对一 : 关联 : 使用associatio…...

微电网优化:基于肝癌算法(Liver Cancer algorithm, LCA)的微电网优化(提供MATLAB代码)
一、微电网优化模型 微电网是一个相对独立的本地化电力单元,用户现场的分布式发电可以支持用电需求。为此,您的微电网将接入、监控、预测和控制您本地的分布式能源系统,同时强化供电系统的弹性,保障您的用电更经济。您可以在连接…...

VUE_H5页面跳转第三方地图导航,兼容微信浏览器
当前项目是uniapp项目,若不是需要替换uni.showActionSheet选择api onMap(address , organName , longitude 0, latitude 0){var ua navigator.userAgent.toLowerCase();var isWeixin ua.indexOf(micromessenger) ! -1;if(isWeixin) {const mapUrl_tx "…...

智慧安全运营:智能化运维,确保服务无忧
智慧安全运营:智能化运维,确保服务无忧 中国联通新一代全球智云数据中心采用先进的智能化运维管理系统,实现对数据中心设施、IT设备、能源消耗、环境参数等全方位、实时监控。通过物联网技术、人工智能算法以及大数据分析,运维团…...

R-tree总结
引言: 在处理空间数据和地理信息系统(GIS)中,高效的空间索引机制对于提升查询性能至关重要。R-tree是一种流行的平衡树数据结构,专门用于索引多维信息,如二维的地理坐标或三维的物体位置。它以其灵活性、高…...

Python 与机器学习,在服务器使用过程中,常用的 Linux 命令包括哪些?
🍉 CSDN 叶庭云:https://yetingyun.blog.csdn.net/ 本博客旨在分享在实际开发过程中,开发者需要了解并熟练运用的 Linux 操作系统常用命令。Linux 作为一种操作系统,与 Windows 或 MacOS 并驾齐驱,尤其在服务器和开发环…...

js通过Object.defineProperty实现数据响应式
目录 数据响应式属性描述符propertyResponsive 依赖收集依赖队列寻找依赖 观察器 派发更新Observer完整代码关于数据响应式关于Object.defineProperty的限制 数据响应式 假设我们现在有这么一个页面 <!DOCTYPE html> <html lang"en"><head><m…...
docker最简单教程(使用dockerfile构建环境)
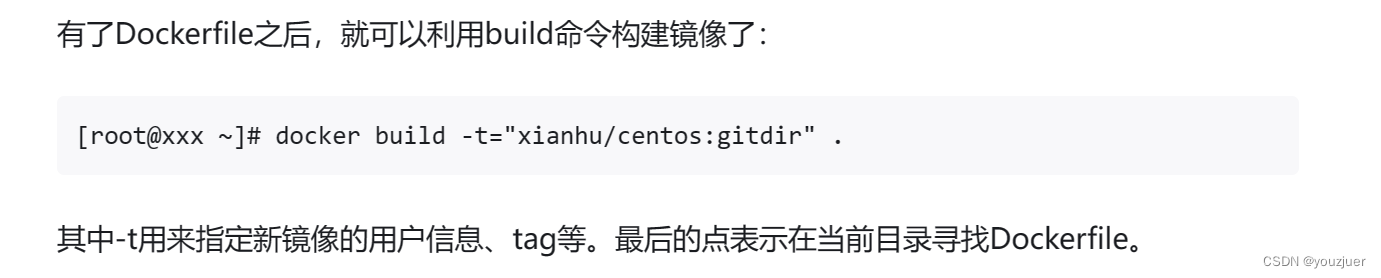
一 手里有的东西 安装好的docker+dockerfile 二 操作 只需要在你的dockerfile文件下执行命令 docker build -t="xianhu/centos:gitdir" . 将用户名、操作系统和tag进行修改就可以了,这就相当于在你本地安装了一个docker环境,然后执行 docker run -it xianhu/ce…...

Vue2 —— 学习(三)
目录 一、绑定 class 样式 (一)字符串写法 1.流程介绍 2.代码实现 (二)数组写法 1.流程介绍 2.代码实现 (三)对象写法 1.流程介绍 2.代码实现 二、绑定 style 样式(了解ÿ…...
Qt Creator 12.0.2 debug 无法查看变量的值 Expression too Complex
鼠标放在局部变量上提示“expression too complex”。 在调试窗口也看不到局部变量的值。 这应该是qt的一个bug,https://bugreports.qt.io/browse/QTCREATORBUG-24180 暂时解决方法: 如下图,需要右键项目然后执行"Clean"和&quo…...
LeetCode-Java:303、304区域检索(前缀和)
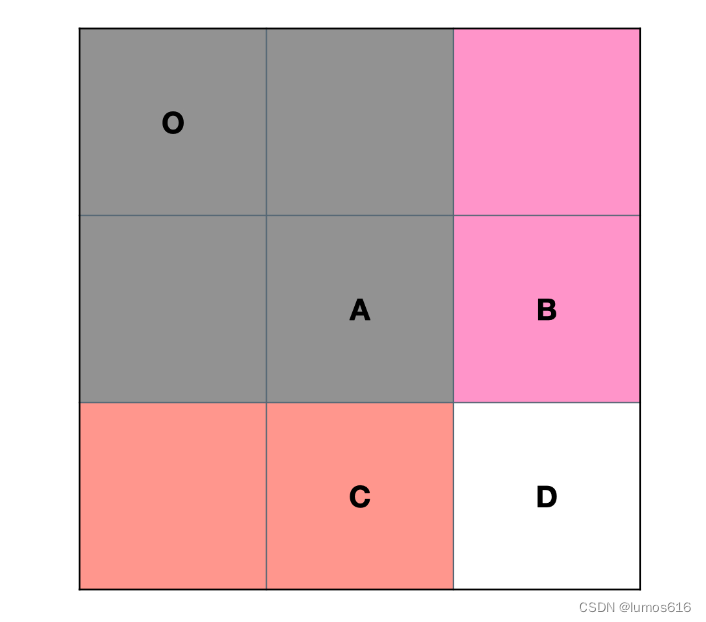
文章目录 题目303、区域和检索(数组不可变)304、二维区域和检索(矩阵不可变) 解①303,一维前缀和②304,二维前缀和 算法前缀和一维前缀和二维前缀和 题目 303、区域和检索(数组不可变ÿ…...

出海业务的网络安全挑战
出海业务的扩展带来了巨大的市场机遇,同时也带来了不少网络安全挑战: 数据泄露与隐私保护:跨境数据传输增加了数据被截获和泄露的风险。地理位置限制和审查:某些地区的网络审查和地理位置限制可能阻碍企业正常开展业务。网络攻击…...

蓝桥杯考前准备— — c/c++
蓝桥杯考前准备— — c/c 对于输入输出函数 如果题目中有要求规定输入数据的格式与输出数据的格式,最好使用scanf()和prinrf()函数。 例如:输入的数据是 2020-02-18,则使用scanf("%d-%d-%d",&year,&mouth,&day)即可…...
【MATLAB源码-第4期】基于MATLAB的1024QAM误码率曲线,以及星座图展示。
1、算法描述 正交幅度调制(QAM,Quadrature Amplitude Modulation)是一种在两个正交载波上进行幅度调制的调制方式。这两个载波通常是相位差为90度(π/2)的正弦波,因此被称作正交载波。这种调制方式因此而得…...
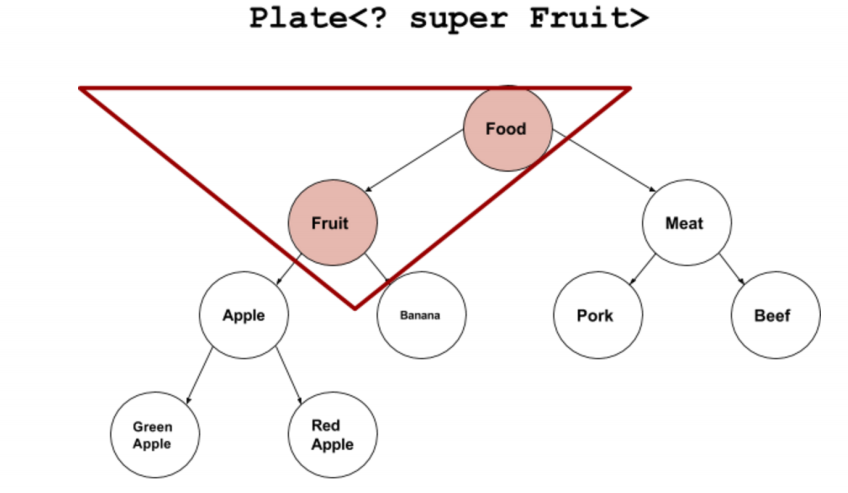
数据结构-----枚举、泛型进阶(通配符?)
文章目录 枚举1 背景及定义2 使用3 枚举优点缺点4 枚举和反射4.1 枚举是否可以通过反射,拿到实例对象呢? 5 总结 泛型进阶1 通配符 ?1.1 通配符解决什么问题1.2 通配符上界1.3 通配符下界 枚举 1 背景及定义 枚举是在JDK1.5以后引入的。主要用途是&am…...

线上问题监控 Sentry 接入全过程
背景: 线上偶发问题出现后 ,测试人员仅通过接口信息无法复现错误场景;并且线上环境的监控,对于提高系统的稳定性 (降低脱发率) 至关重要;现在线上监控工具这个多,为什么选择Sentry?…...
基础】以MySQL为例的数据库基础)
【数据库(MySQL)基础】以MySQL为例的数据库基础
文章目录 0. 本文用到的emp表,dept表,salgrade表1. MySQL入门2. 简单查询3. 字段计算4. 条件查询4.1 and4.2 null4.3 or4.4 and和or的优先级4.4 in 和 not in4.5 模糊查询 5. 排序5.1 简单排序5.2 两个字段排序5.3 综合排序 6. 一些常用函数6.1 大小写转换6.2 substr子字符串6.…...
权限修饰符,代码块,抽象类,接口.Java
1,权限修饰符 权限修饰符:用来控制一个成员能够被访问的范围可以修饰成员变量,方法,构造方法,内部类 👻👗👑权限修饰符的分类 🧣四种作用范围由小到大(private<空着…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

聊聊 Pulsar:Producer 源码解析
一、前言 Apache Pulsar 是一个企业级的开源分布式消息传递平台,以其高性能、可扩展性和存储计算分离架构在消息队列和流处理领域独树一帜。在 Pulsar 的核心架构中,Producer(生产者) 是连接客户端应用与消息队列的第一步。生产者…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

P3 QT项目----记事本(3.8)
3.8 记事本项目总结 项目源码 1.main.cpp #include "widget.h" #include <QApplication> int main(int argc, char *argv[]) {QApplication a(argc, argv);Widget w;w.show();return a.exec(); } 2.widget.cpp #include "widget.h" #include &q…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

MySQL 知识小结(一)
一、my.cnf配置详解 我们知道安装MySQL有两种方式来安装咱们的MySQL数据库,分别是二进制安装编译数据库或者使用三方yum来进行安装,第三方yum的安装相对于二进制压缩包的安装更快捷,但是文件存放起来数据比较冗余,用二进制能够更好管理咱们M…...

Selenium常用函数介绍
目录 一,元素定位 1.1 cssSeector 1.2 xpath 二,操作测试对象 三,窗口 3.1 案例 3.2 窗口切换 3.3 窗口大小 3.4 屏幕截图 3.5 关闭窗口 四,弹窗 五,等待 六,导航 七,文件上传 …...

如何应对敏捷转型中的团队阻力
应对敏捷转型中的团队阻力需要明确沟通敏捷转型目的、提升团队参与感、提供充分的培训与支持、逐步推进敏捷实践、建立清晰的奖励和反馈机制。其中,明确沟通敏捷转型目的尤为关键,团队成员只有清晰理解转型背后的原因和利益,才能降低对变化的…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
