计算机网络—HTTPS协议详解:工作原理、安全性及应用实践

🎬慕斯主页:修仙—别有洞天
♈️今日夜电波:ヒューマノイド—ずっと真夜中でいいのに。
1:03━━━━━━️💟──────── 5:06
🔄 ◀️ ⏸ ▶️ ☰
💗关注👍点赞🙌收藏您的每一次鼓励都是对我莫大的支持😍
目录
什么是HTTPS?
加密
加密和解密的概念
常见的加密方式
HTTPS的工作过程的探究
只使用对称加密
只使用非对称加密
双方都使用非对称加密
非对称加密+对称加密
中间人攻击问题
引⼊证书
CA认证
理解数据签名
非对称加密+对称加密+证书认正
中间⼈有没有可能篡改该证书?
中间⼈整个掉包证书?
什么是HTTPS?
HTTP协议内容都是按照文本形式进行明文传输的,这样就会导致在传输过程中出现一些篡改的情况。而HTTPS(Hypertext Transfer Protocol Secure)是一种透过计算机网络进行安全通信的传输协议,他则是在HTTP的基础上加上了一层加密层,通常在应用层和传输层之间加一层软件层(一般称为 SSL /TLS)。HTTPS因此也通常称为HTTP over TLS或HTTP over SSL。这种协议在HTTP的基础上,利用SSL/TLS来加密数据包,从而提供对网站服务器的身份认证,保护交换数据的隐私与完整性。大致的图解如下:
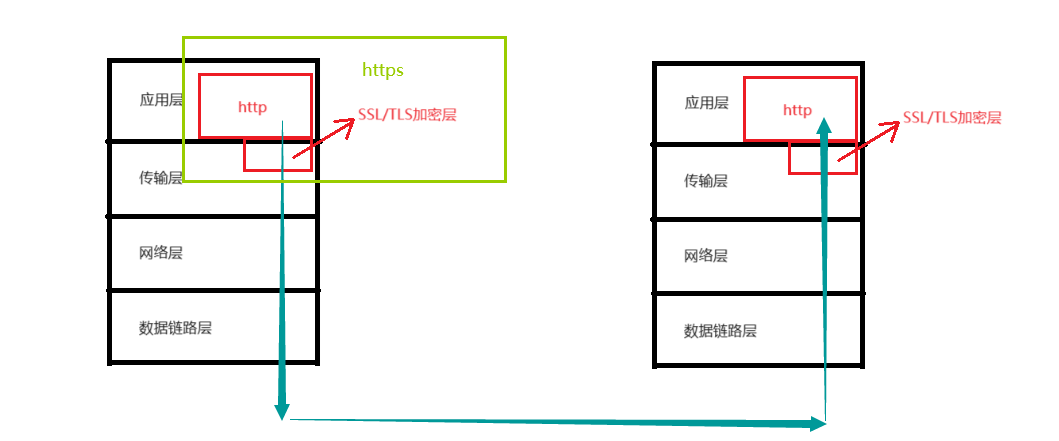
加密
加密和解密的概念
加密就是把明文信息经过一系列的转换从而生成密文。例如:我们可以可以在客户端传输给服务端的过程中用5^明文,那么这就称为密文。
解密就是把密文信息再进行经过一系列的装换从而变回明文。例如:上面我们提到的密文例子,我们可以再使用5^密文,就变回了原来的明文。
常见的加密方式
在HTTPS中,常见的加密方式包括:
- 对称加密算法:对称加密使用相同的密钥进行加密和解密。常见的对称加密算法包括AES(高级加密标准)和DES(数据加密标准)。
- 特点:算法公开、计算量小、加密速度快、加密效率高
- 非对称加密算法:非对称加密使用一对密钥,分为公钥和私钥。公钥用于加密,私钥用于解密。常见的非对称加密算法包括RSA、DSA和ECC(椭圆曲线加密)。
- 特点:算法强度复杂、安全性依赖于算法与密钥但是由于其算法复杂,而使得加密解密速度没有对称加密解密的速度快。
- 当然我们可以使用公钥加密,只能用私钥解密,使用私钥加密只能用公钥解密。
- 由于公钥是公开的,因此我们所有人都可以使用公钥进行加密和解密。
- 如果我们使用私钥加密,那么只要拥有公钥的人都可以解密。但是,如果我们使用公钥加密,那么只有拥有私钥的人才能解密。
- 消息认证码(MAC):MAC用于验证消息的完整性和真实性。常见的MAC算法包括HMAC(基于散列的消息认证码)。
- 数字签名:数字签名用于验证消息的发送者和完整性。常见的数字签名算法包括RSA和DSA。
在HTTPS连接中,通常会结合使用这些加密方式,以确保通信的机密性、完整性和认证性。
HTTPS的工作过程的探究
只使用对称加密
使用只有对称加密的HTTPS连接存在一个关键问题:密钥交换和管理。
在对称加密中,加密和解密使用相同的密钥。这意味着服务器和客户端需要共享同一个密钥来加密和解密通信。然而,在一个开放的网络环境中,安全地共享密钥是非常困难的。如果密钥在传输过程中被截获或泄露,那么整个通信链路就会被暴露,安全性受到威胁。
例如:如果通讯算法各持有同一个密匙,并且除了双方没人知道。这样双方的通信安全当热可以保证。但是真的这么简单吗?我们该如何保证客户端和服务器双方使用的是同一个密匙?如果是内置的,内置在浏览器亦或者操作系统中,无论是哪一个都有办法被黑客所获取。如果不是内置的,那么我们在将密匙传输的过程中也是会有安全隐患的。
只使用非对称加密
只使用非对称加密的HTTPS连接也存在一些问题,主要包括:
- 性能问题:非对称加密算法通常比对称加密算法更复杂,因此加密和解密的计算成本更高。这可能会导致HTTPS连接的性能下降,特别是对于高流量的网站或服务而言。
- 密钥长度问题:为了提高安全性,通常需要较长的密钥长度。较长的密钥长度会增加加密和解密的计算复杂度,进一步影响性能。
- 密钥交换问题:虽然非对称加密可以解决密钥交换和管理的问题,但仍然存在一些挑战。密钥交换需要在通信的开始阶段进行,并且涉及到公钥的传输。如果攻击者能够截获或篡改公钥的传输,就可能导致安全性问题。例如:我们服务器持有私钥,而服务器先把公钥以明文方式传输给浏览器,之后浏览器向服务器传数据前都先用这个公钥加密好再传。但是在传输的时候浏览器公钥被黑客截取了,这个时候,黑客就可以在这个传输过程中获得来着服务器的信息了。
- 中间人攻击:在只使用非对称加密的情况下,仍然存在中间人攻击的风险。攻击者可能会伪装成合法的服务器或客户端,并与另一方建立加密连接,从而截获或篡改通信内容。
双方都使用非对称加密
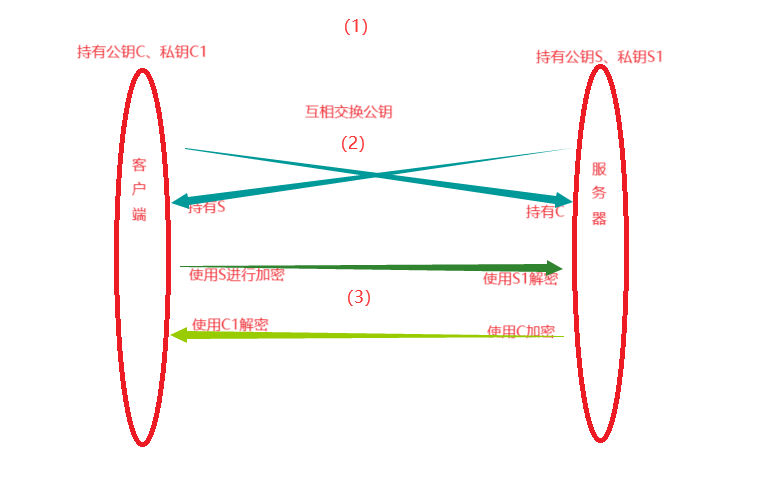
我们让服务器和客户端都都持有各自独特的公钥和私钥,即:每个通信实体都有一对公钥和私钥。通常的流程如下:
(1)服务器持有公钥S、私钥S1,客户端持有公钥C、私钥C1。
(2)客户端与服务器通信前,互相交换自己所持有的公钥。
(3)若客户端给服务器发消息就使用公钥S加密,后续只能服务器使用秘钥S1解密,若服务器给客户端发消息则使用公钥C加密,只能由客户端用秘钥C1解密。
大致的图示如下:
这种做法看似是安全的,但是双方使用非对称加密可能会导致通信的性能下降,特别是对于大量通信或需要实时性的应用而言。并且仍然存在安全的问题(后面详讲):虽然双方都使用非对称加密,但仍然存在中间人攻击的风险。攻击者可能会伪装成合法的通信实体,并与另一方建立加密连接,从而截获或篡改通信内容。使用非对称加密的安全性依赖于公钥的安全性。如果公钥被截获或篡改,通信的安全性将受到威胁。
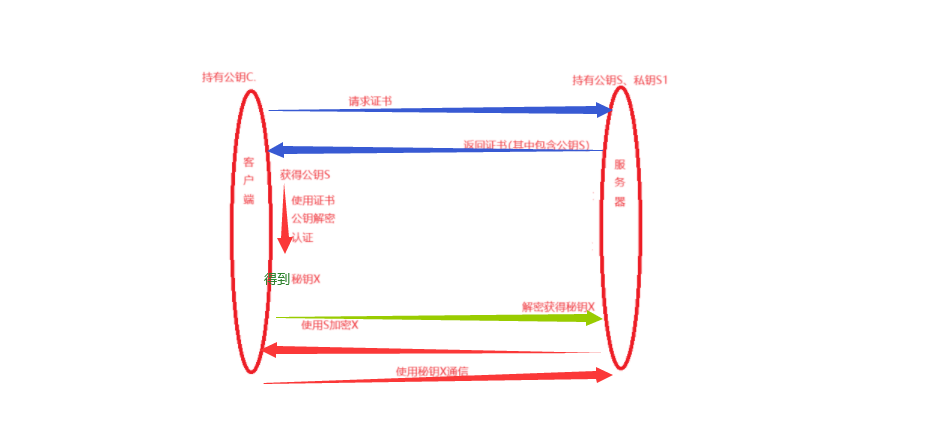
非对称加密+对称加密
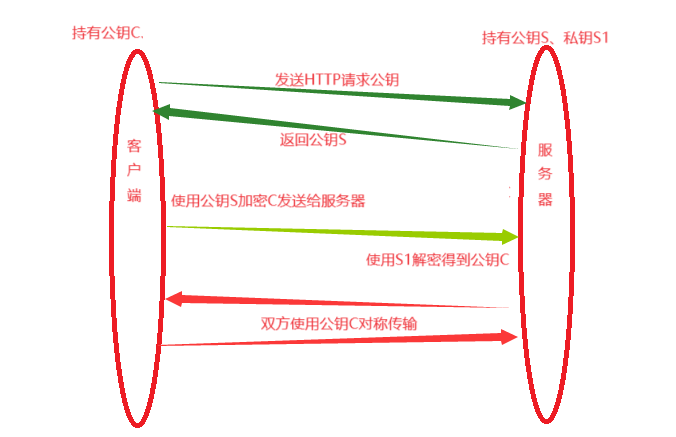
结合非对称加密和对称加密是一种常见且有效的做法,通常被用于保障通信的安全性和效率。这种组合利用了两种加密方式的优点,解决了各自的缺点。通常的流程如下:
(1)服务器持有公钥S、私钥S1,客户端持有公钥C。
(2)客户端向服务器发送请求,服务器响应返回公钥S。
(3)客户端获取S,并使用公钥C加密,然后发送给服务器。
(4)服务器使用私钥S1解密得到公钥C,双方使用公钥C进行对称加密传输。
大致图示如下:
然而这样依旧存在问题,这里存在着中间人攻击的问题(MITM):
- 尽管使用了非对称加密进行密钥交换,但仍然存在中间人攻击的风险。攻击者可能伪装成合法的通信实体,与双方建立加密连接,并对通信内容进行篡改或监视。
中间人攻击问题
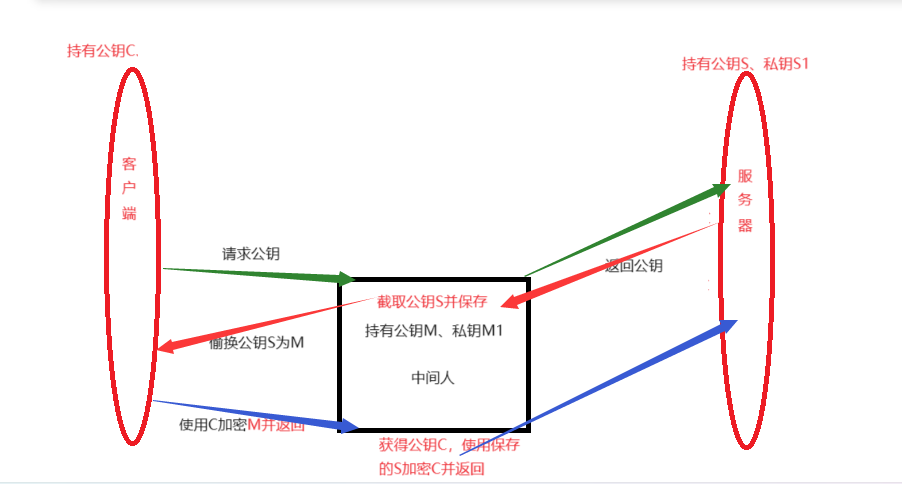
我们首先明确以下开始的条件:
服务器拥有非对称加密的公钥S、S1,客户端拥有对称加密的公钥C、中间人拥有非对称加密的公钥M、M1。
接下来开始正式的操作:
(这个中间人可能是处于浏览器中也可能处于非法的软件中等等等等,这里认为在浏览器中)客户端经过浏览器向服务器请求公钥,服务器因此经过浏览器向客户端返回公钥S,但是这个时候中间人将S从报文中拿出来保存好并且把自己的公钥M填入报文中并且返回了客户端(然而客户端并不知道报文已经被替换过了)。客户端得到公钥M,使用M加密公钥C经过浏览器返回给服务器。然而在这个过程中中间人就可以通过自己的秘钥M1提取公钥C。再公钥C和曾经保存的公钥S进行加密后填入报文推送给服务器。在完成这个操作够,双方开始通信,这个时候之间人既能同时掌握双方的信息,可以对这些数据进行监听甚至直接进行修改植入自己的程序!!!
大致的图示如下:
上面的攻击方案,同样适用于仅使用非对称加密和双方都使用非对称加密。
那么中间人可以攻击的核心原因是什么呢?这是因为客户端无法验证公钥的合法性!!!
引⼊证书
CA认证
服务端在使⽤HTTPS前,需要向CA机构申领⼀份数字证书,数字证书⾥含有证书申请者信息(犯法直接线下真实)、公钥信息等。服务器把证书传输给浏览器,浏览器从证书⾥获取公钥就⾏了,证书就如⾝份证,证明服务端公钥的权威性。这份数组证书就是为了解决上述的问题。他的本质实际上就是数据!
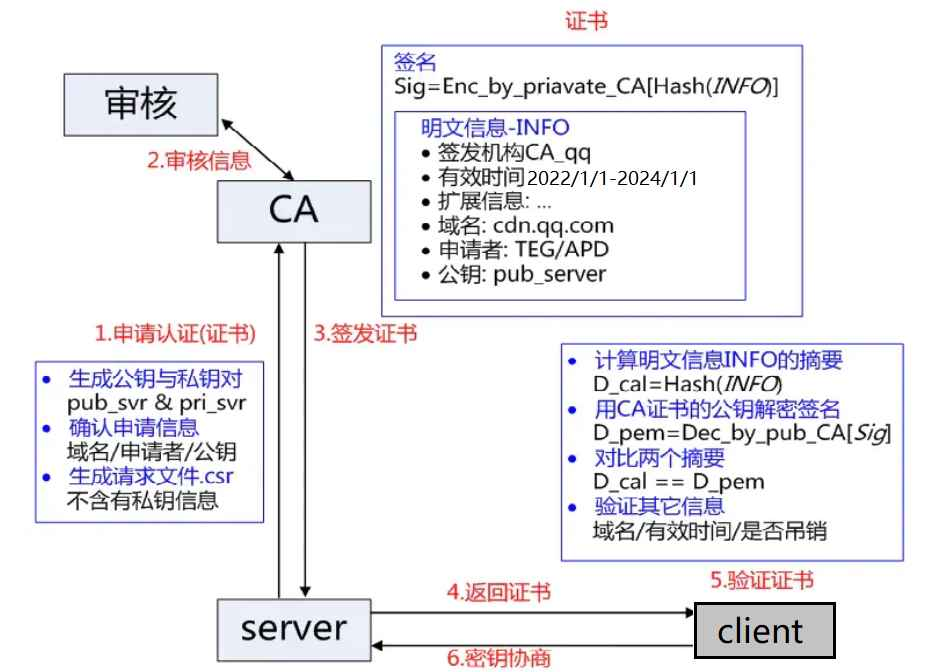
这个证书可以理解成是⼀个结构化的字符串,⾥⾯包含了以下信息:
• 证书发布机构
• 证书有效期
• 公钥
• 证书所有者
• 签名
• ......
需要注意的是:申请证书的时候,需要在特定平台⽣成查,会同时⽣成⼀对⼉密钥对⼉,即公钥和私钥。这对密钥对⼉就是⽤来在⽹络通信中进⾏明⽂加密以及数字签名的。其中公钥会随着CSR⽂件,⼀起发给CA进⾏权威认证,私钥服务端⾃⼰保留,⽤来后续进⾏通信(其实主要就是⽤来交换对称秘钥)。
理解数据签名
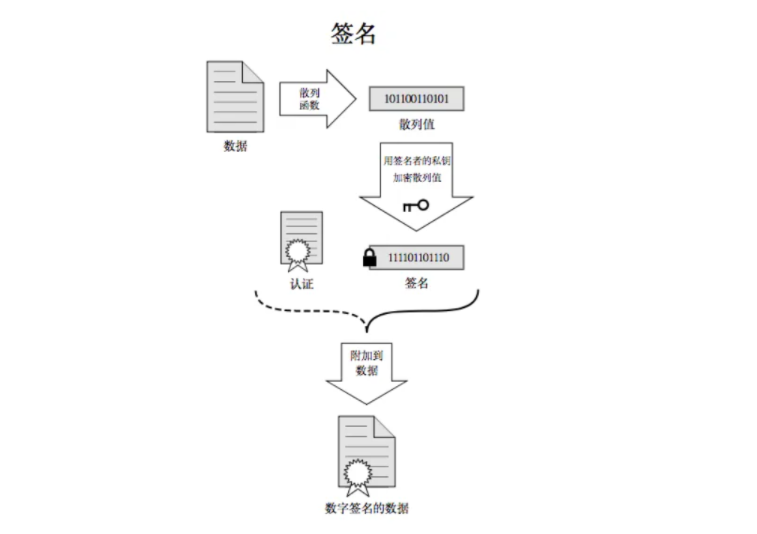
签名的形成是基于⾮对称加密算法的,注意,⽬前暂时和https没有关系,不要和https中的公钥私钥搞混,大致的过程是对于大文本进行摘要,再对摘要的信息进行加密。
这个加密的过程大致如下:将提交上来的数据经过哈希散列数据摘要(数据包含了原始数据的抽象表示。哈希函数将原始数据转换为一个固定长度的二进制字符串,这个字符串就是数据摘要,也称为哈希值或消息摘要),形成对应的散列值,然后CA机构会使用自己的私钥进行加密,加密后则被称为签名,再将原始的文本和签名结合,形成签名的数据,这个过程成为颁发证书。
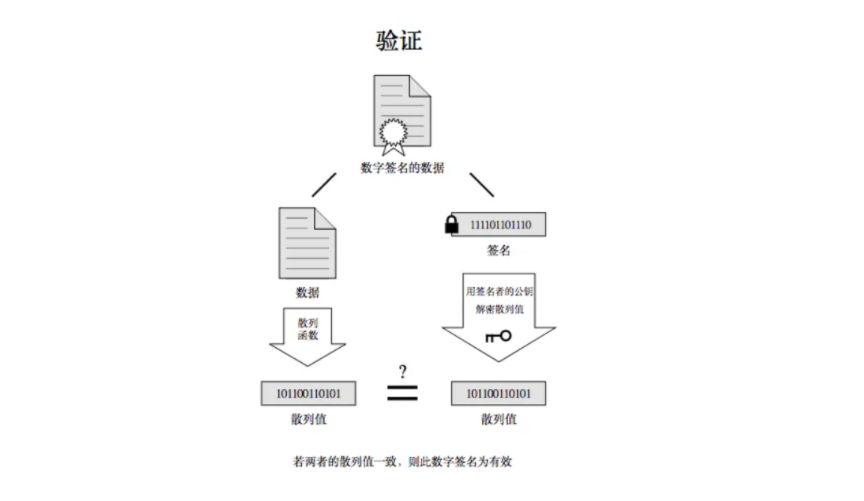
后续再将这个证书给服务端,再由服务端把证书给客户端。但是,服务端向客户端返回证书的时候,也可以被中间人篡改啊!那么如何保证客户端的证书是没有被篡改过的呢?客户端会将证书拆分开来分为明文部分和签名,明文部分进行散列函数md5形成数据摘要,由于签名是经过数据摘要和 CA机构 的私钥 加密过的,因此再由CA机构的公钥(这个公钥通常会内置客户端中)进行解密,后续比对这两部分的散列值即可,图示如下:
当服务端申请CA证书的时候,CA机构会对该服务端进⾏审核,并专⻔为该⽹站形成数字签名,过程如下:
- CA机构拥有⾮对称加密的私钥A和公钥A
- CA机构对服务端申请的证书明⽂数据进⾏hash,形成数据摘要
- 然后对数据摘要⽤CA私钥A'加密,得到数字签名S
服务端申请的证书明⽂和数字签名S共同组成了数字证书,这样⼀份数字证书就可以颁发给服务端了
非对称加密+对称加密+证书认正
客户端进行请求,服务器返回证书。客户端认证证书的合法性,并且得到服务端公钥S,并且客户端形成对称秘钥X与公钥S进行加密推送回服务器,然后服务器使用S1进行解密得到秘钥X,最后双方使用秘钥X进行通信。
大致图示如下:
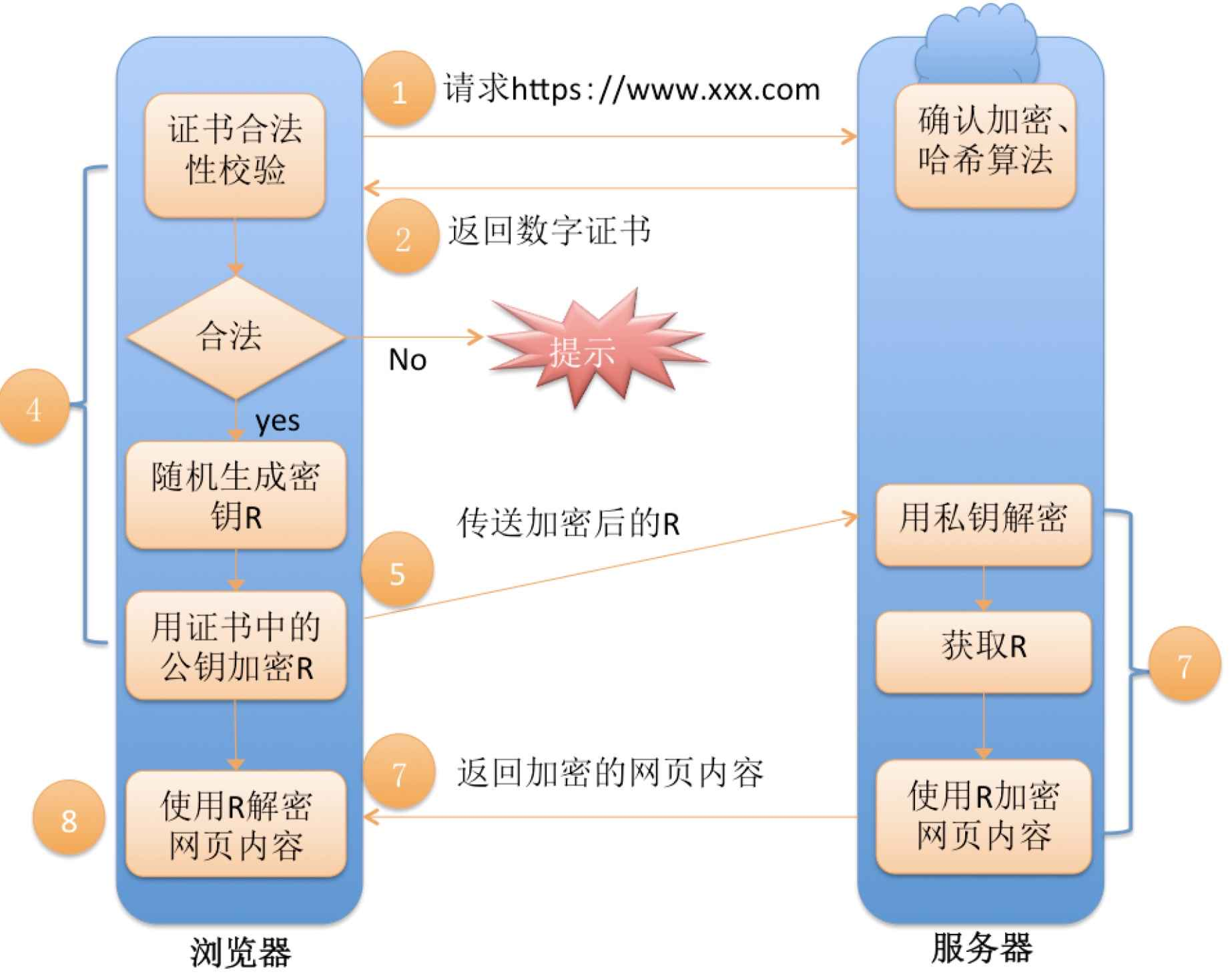
一些问题:
中间⼈有没有可能篡改该证书?
• 中间⼈篡改了证书的明⽂
• 由于他没有CA机构的私钥,所以⽆法hash之后⽤私钥加密形成签名,那么也就没法办法对篡改后的证书形成匹配的签名
• 如果强⾏篡改,客⼾端收到该证书后会发现明⽂和签名解密后的值不⼀致,则说明证书已被篡改,证书不可信,从⽽终⽌向服务器传输信息,防⽌信息泄露给中间⼈
中间⼈整个掉包证书?
• 因为中间⼈没有CA私钥,所以⽆法制作假的证书(为什么?)因为只有CA机构才掌握私钥。中间人没有CA的私钥,他们无法生成有效的数字签名来伪造证书。
• 所以中间⼈只能向CA申请真证书,然后⽤⾃⼰申请的证书进⾏掉包
• 这个确实能做到证书的整体掉包,但是别忘记,证书明⽂中包含了域名等服务端认证信息,如果整体掉包,客⼾端依旧能够识别出来。
• 永远记住:中间⼈没有CA私钥,所以对任何证书都⽆法进⾏合法修改,包括⾃⼰的
感谢你耐心的看到这里ღ( ´・ᴗ・` )比心,如有哪里有错误请踢一脚作者o(╥﹏╥)o!

给个三连再走嘛~
相关文章:

计算机网络—HTTPS协议详解:工作原理、安全性及应用实践
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:ヒューマノイド—ずっと真夜中でいいのに。 1:03━━━━━━️💟──────── 5:06 🔄 ◀️ ⏸…...

卫星遥感影像在农业方面的应用及评价
一、引言 随着科技的进步,卫星遥感技术在农业领域的应用越来越广泛。卫星遥感技术以其宏观、快速、准确的特点,为农业生产和管理提供了有力的技术支撑。本文将对卫星遥感在农业方面的应用进行详细介绍,并通过具体案例进行说明。 二、…...
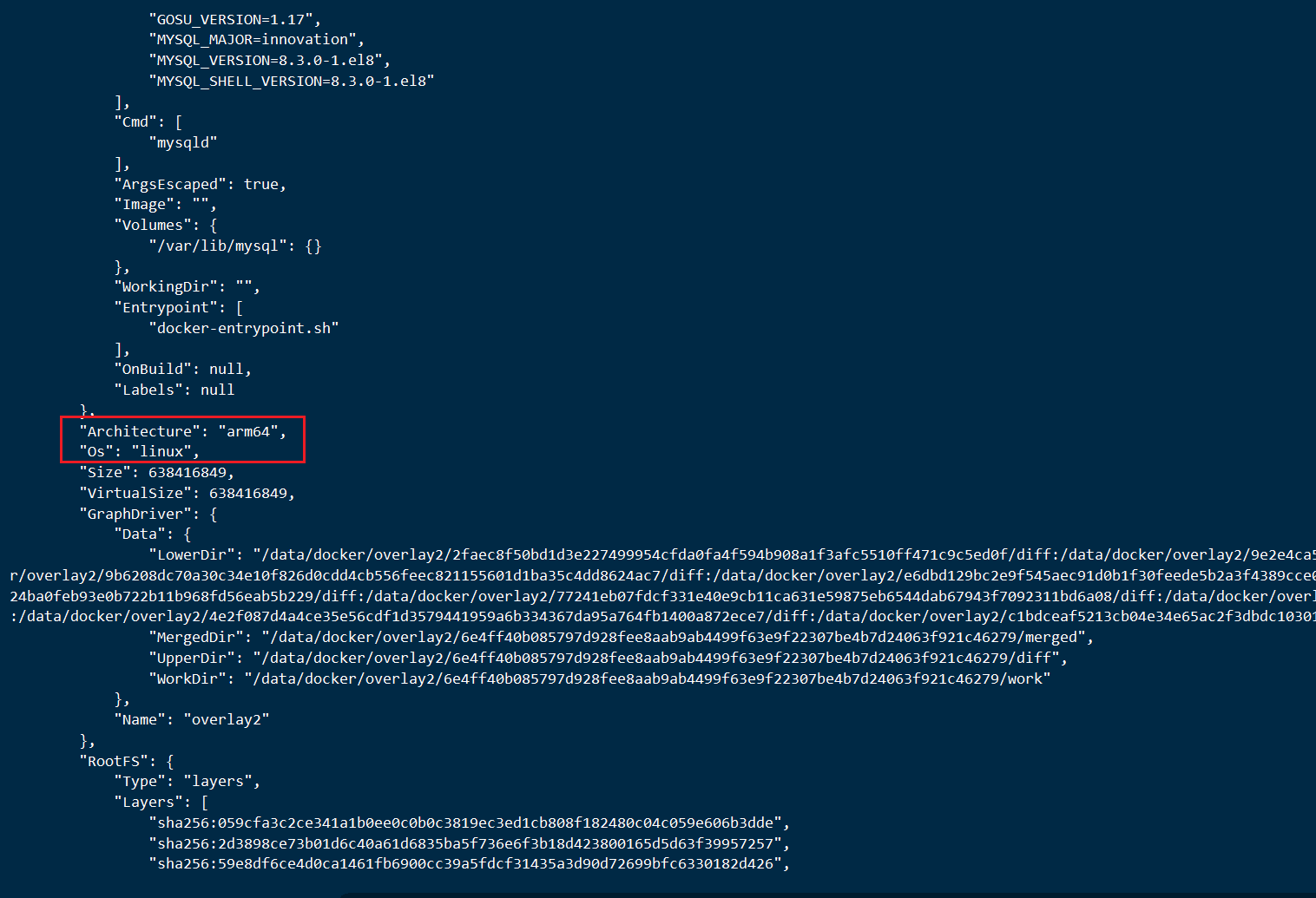
docker pull镜像的时候指定arm平台
指定arm平台 x86平台下载arm平台的镜像包 以mysql镜像为例 docker pull --platform linux/arm64 mysqldocker images查看镜像信息 要查看Docker镜像的信息,可以使用docker inspect命令。这个命令会返回镜像的详细信息,包括其元数据和配置。 docker i…...

如何通过OceanBase V4.2 动态采样优化查询性能
OceanBase v4.2 推出了优化器动态采样的功能,在SQL运行过程中,该功能会收集需要的统计信息,协助优化器制定出更好的执行计划,进一步提升了查询性能。 影响查询性能的因素是什么?为何你的优化器效果不佳? …...
Vue3---基础1(认识,创建)
变化 相对于Vue2,Vue3的变化: 性能的提升 打包大小减少 41% 初次渲染快 55%,更新渲染快133% 内存减少54% 源码的升级 使用 proxy 代替 defineProperty 实现响应式 重写虚拟 DOM 的实现和 Tree-shaking TypeScript Vue3就可以更好的支持TypeSc…...

JAVA集合ArrayList
目录 ArrayList概述 add(element) 用法 add(index, element)用法 remove(element)用法 remove(index)用法 get(index)用法 set(index,element) 练习 test1 定义一个集合,添加字符串,并进行遍历&…...

Bitmap OOM
老机器Bitmap预读仍然OOM,无奈增加一段,终于不崩溃了。 if (Build.VERSION.SDK_INT < 21)size 2; 完整代码: Bitmap bitmap; try {//Log.e(Thread.currentThread().getStackTrace()[2] "", surl);URL url new URL(surl);…...

基于深度学习的人脸表情识别系统(PyQT+代码+训练数据集)
基于深度学习的人脸表情识别系统(PyQT代码训练数据集) 前言一、数据集1.1 数据集介绍1.2 数据预处理 二、模型搭建三、训练与测试3.1 模型训练3.2 模型测试 四、PyQt界面实现 前言 本项目是基于mini_Xception深度学习网络模型的人脸表情识别系统&#x…...

Qt 中的项目文件解析和命名规范
🐌博主主页:🐌倔强的大蜗牛🐌 📚专栏分类:QT❤️感谢大家点赞👍收藏⭐评论✍️ 目录 一、Qt项目文件解析 1、.pro 文件解析 2、widget.h 文件解析 3、main.cpp 文件解析 4、widget.cpp…...

【chatGPT】我:在Cadence Genus软件中,出现如下问题:......【4】
我 在Cadence Genus中,tcl代码为:foreach clk $clk_list{ set clkName [lindex $clk_list 0] set targetFreq [lindex $clk_list 1] set uncSynth [lindex $clk_list 4] set clkPeriod [lindex “%.3f” [expr 1 / $targetFreq]] … } 以上代码出现如下…...
在JAVA中的应用)
单例模式(Singleton Pattern)在JAVA中的应用
在软件开发中,设计模式是解决特定问题的一种模板或者指南。它们是在多年的软件开发实践中总结出的有效方法。JAVA设计模式广泛应用于各种编程场景中,以提高代码的可读性、可维护性和扩展性。本文将介绍单例模式,这是一种常用的创建型设计模式…...

手把手教你创建新的OpenHarmony 三方库
创建新的三方库 创建 OpenHarmony 三方库,建议使用 Deveco Studio,并添加 ohpm 工具的环境变量到 PATH 环境变量。 创建方法 1:IDE 界面创建 在现有应用工程中,新创建 Module,选择"Static Library"模板&a…...

从零开始,如何成功进入IT行业?
0基础如何进入IT行业? 简介:对于没有任何相关背景知识的人来说,如何才能成功进入IT行业?是否有一些特定的方法或技巧可以帮助他们实现这一目标? 在当今数字化时代,IT行业无疑是一个充满活力和机遇的领域。…...
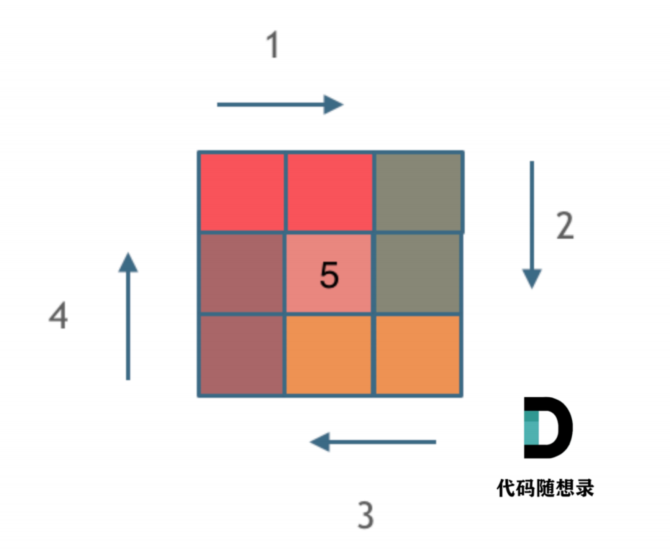
【数组】5螺旋矩阵
这里写自定义目录标题 一、题目二、解题精髓-循环不变量三、代码 一、题目 给定⼀个正整数 n,⽣成⼀个包含 1 到 n^2 所有元素,且元素按顺时针顺序螺旋排列的正⽅形矩阵。 示例: 输⼊: 3 输出: [ [ 1, 2, 3 ], [ 8, 9, 4 ], [ 7, 6, 5 ] ] 二、解题精髓…...

Sora视频生成模型:开启视频创作新纪元
随着人工智能技术的飞速发展,视频生成领域也迎来了前所未有的变革。Sora视频生成模型作为这一领域的佼佼者,凭借其卓越的性能和创新的应用场景,受到了广泛的关注与好评。本文将对Sora视频生成模型进行详细介绍,带您领略其魅力所在…...
OpenAI现已普遍提供带有视觉应用程序接口的GPT-4 Turbo
OpenAI宣布,其功能强大的GPT-4 Turbo with Vision模型现已通过公司的API全面推出,为企业和开发人员将高级语言和视觉功能集成到其应用程序中开辟了新的机会。 PS:使用Wildcard享受不受网络限制的API调用,详情查看教程 继去年 9 月…...

Swift中的元组属性
在Swift中,元组属性指的是一个元组作为结构体、类或枚举的属性。可以将一个元组作为属性来存储和访问多个值。 例如,考虑以下的Person类: class Person {var name: Stringvar age: Intvar address: (String, Int)init(name: String, age: I…...

【go从入门到精通】作用域,包详解
作者简介: 高科,先后在 IBM PlatformComputing从事网格计算,淘米网,网易从事游戏服务器开发,拥有丰富的C,go等语言开发经验,mysql,mongo,redis等数据库,设计模…...
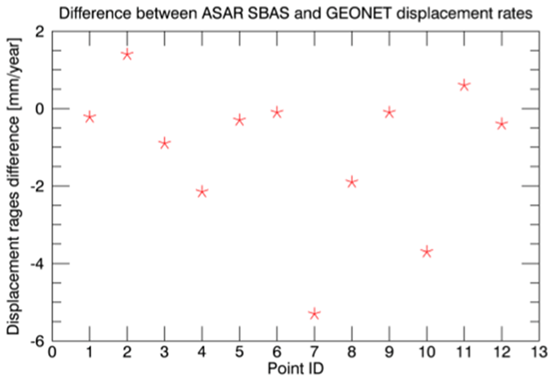
利用SARscape对日本填海造陆和天然气开采进行地表形变监测
日本千叶市,是日本南部重要的工业港市。位于西部的浦安市是一个典型的"填海造田"城市,东南部的东金区有一片天然气开采区域,本文利用SARscape,用干涉叠加的方法,即PS和SBAS,对这两个区域进行地表…...

“Python爬虫实战:高效获取网上公开美图“
如何通过Python创建一个简单的网络爬虫,以爬取网上的公开图片。网络爬虫是一种自动化工具,能够浏览互联网、下载内容并进行处理。请注意,爬取内容时应遵守相关网站的使用条款,尊重版权和隐私权。 ### 网络爬虫简介 网络爬虫&…...

Qt Http Server模块功能及架构
Qt Http Server 是 Qt 6.0 中引入的一个新模块,它提供了一个轻量级的 HTTP 服务器实现,主要用于构建基于 HTTP 的应用程序和服务。 功能介绍: 主要功能 HTTP服务器功能: 支持 HTTP/1.1 协议 简单的请求/响应处理模型 支持 GET…...

反射获取方法和属性
Java反射获取方法 在Java中,反射(Reflection)是一种强大的机制,允许程序在运行时访问和操作类的内部属性和方法。通过反射,可以动态地创建对象、调用方法、改变属性值,这在很多Java框架中如Spring和Hiberna…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

return this;返回的是谁
一个审批系统的示例来演示责任链模式的实现。假设公司需要处理不同金额的采购申请,不同级别的经理有不同的审批权限: // 抽象处理者:审批者 abstract class Approver {protected Approver successor; // 下一个处理者// 设置下一个处理者pub…...

人机融合智能 | “人智交互”跨学科新领域
本文系统地提出基于“以人为中心AI(HCAI)”理念的人-人工智能交互(人智交互)这一跨学科新领域及框架,定义人智交互领域的理念、基本理论和关键问题、方法、开发流程和参与团队等,阐述提出人智交互新领域的意义。然后,提出人智交互研究的三种新范式取向以及它们的意义。最后,总结…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

android13 app的触摸问题定位分析流程
一、知识点 一般来说,触摸问题都是app层面出问题,我们可以在ViewRootImpl.java添加log的方式定位;如果是touchableRegion的计算问题,就会相对比较麻烦了,需要通过adb shell dumpsys input > input.log指令,且通过打印堆栈的方式,逐步定位问题,并找到修改方案。 问题…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...
