[蓝桥杯 2018 省 A] 付账问题
【蓝桥杯】付账问题
[蓝桥杯 2018 省 A] 付账问题
题目描述
几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。
现在有 n n n 个人出去吃饭,他们总共消费了 S S S 元。其中第 i i i 个人带了 a i a_i ai 元。幸运的是,所有人带的钱的总数是足够付账的,但现在问题来了:每个人分别要出多少钱呢?
为了公平起见,我们希望在总付钱量恰好为 S S S 的前提下,最后每个人付的钱的标准差最小。这里我们约定,每个人支付的钱数可以是任意非负实数,即可以不是 1 1 1 分钱的整数倍。你需要输出最小的标准差是多少。
标准差的介绍:标准差是多个数与它们平均数差值的平方平均数,一般用于刻画这些数之间的“偏差有多大”。形式化地说,设第 i i i 个人付的钱为 b i b_i bi 元,那么标准差为 s = 1 n ∑ i = 1 n ( b i − 1 n ∑ i = 1 n b i ) s=\sqrt{\frac{1}{n}\sum_{i=1}^n(b_i-\frac{1}{n}\sum_{i=1}^n b_i)} s=n1∑i=1n(bi−n1∑i=1nbi)
输入格式
第一行包含两个整数 n n n、 S S S;
第二行包含 n n n 个非负整数 a 1 , ⋯ , a n a_1,\cdots,a_n a1,⋯,an。
输出格式
输出到标准输出。
输出最小的标准差,四舍五入保留 4 4 4 位小数。
保证正确答案在加上或减去 1 0 − 9 10^{-9} 10−9 后不会导致四舍五入的结果发生变化。
样例 #1
样例输入 #1
5 2333
666 666 666 666 666
样例输出 #1
0.0000
样例 #2
样例输入 #2
10 30
2 1 4 7 4 8 3 6 4 7
样例输出 #2
0.7928
提示
【样例解释】
- 每个人都出 2333/5 元,标准差为 0。
【数据约定】
对于 10 % 10\% 10% 的数据,所有 a i a_i ai 相等;
对于 30 % 30\% 30% 的数据,所有非 0 0 0 的 a i a_i ai 相等;
对于 60 % 60\% 60% 的数据, n ≤ 1000 n \le 1000 n≤1000;
对于 80 % 80\% 80% 的数据, n ≤ 1 0 5 n \le 10^5 n≤105;
对于所有数据, n ≤ 5 × 1 0 5 , 0 ≤ a i ≤ 1 0 9 n \le 5 \times 10^5,0 \le a_i \le 10^9 n≤5×105,0≤ai≤109。
标签:贪心
思路:
标准差,即数据的分散程度,分散度高标准差大,反之则越小。
我们使标准差小,则尽可能让数据集中在平均数附近
$ a_i<avg(平均数) , 则 ,则 ,则b_i=a_i$ a v g − a i avg-a_i avg−ai为不够的钱,由钱多的均摊
有5个人带的钱为 a 1 , a 2 , a 3 , a 4 , a 5 a_1,a_2,a_3,a_4,a_5 a1,a2,a3,a4,a5,avg为每个人付款的平均数,总付款sum
a 1 a1 a1小于 a v g avg avg,因此他只能付 a 1 a1 a1,多的钱 a v g − a 1 avg-a1 avg−a1由 a 2 到 a 5 a_2到a_5 a2到a5来均摊,
即付款c = s u m − a 1 / ( n − 1 ) =sum-a1/(n-1) =sum−a1/(n−1),如果 c > a 2 c>a2 c>a2,同样 a 2 a2 a2拿出所有的钱,剩下的由后面的均摊,以此类推
#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=5e5+5;
long double money[N];
signed main()
{int n; long double s=0.0;//注意这里,虽然将int定义为long long但输入的是long long 类型时,输入格式一定还是%lld,否则会出错scanf("%lld %Lf",&n,&s);//long double输入输出格式为%Lflong double ave=s/n;//平均数for(int i=0;i<n;i++)scanf("%Lf",&money[i]);sort(money,money+n);long double sum=0,t=0;for(int i=0;i<n;i++)//想让我们的标准差小,每个数尽量集中在平均数附近,先排序,遍历一遍这些数//如果这个数小于平均数,就要拿出全部的值,不够的钱a由钱多于平均数的人去均摊,使后面的人的付钱平均数提高//可能出现因为平均数提高后面的人也拿不出来这么多钱,那我们就让他拿出全部钱,剩下的钱仍由更后面的人去分摊{t=min(s/(n-i),money[i]);//注意min里的参数中数据类型要一致,即int对应int,long double和long double对应sum+=(t-ave)*(t-ave);s-=t;}printf("%.4Lf",sqrt(sum/n));return 0;
}
相关文章:

[蓝桥杯 2018 省 A] 付账问题
【蓝桥杯】付账问题 [蓝桥杯 2018 省 A] 付账问题 题目描述 几个人一起出去吃饭是常有的事。但在结帐的时候,常常会出现一些争执。 现在有 n n n 个人出去吃饭,他们总共消费了 S S S 元。其中第 i i i 个人带了 a i a_i ai 元。幸运的是&#…...
)
设计模式|装饰器模式(Decorator Pattern)
文章目录 结构优缺点优点缺点适用场景示例装饰器模式(Decorator Pattern)是一种结构型设计模式,它允许在不改变原始对象的基础上,动态地给对象添加新的功能或责任。这种模式是通过创建一个包装对象,也就是装饰器,来包裹真实的对象,然后在装饰器中添加新的行为或功能。这…...

发作性睡病有性别差异吗?
发作性睡病是一种特殊的睡眠障碍,以不可控制的嗜睡、猝倒发作、睡眠瘫痪、入睡前幻觉以及夜间睡眠紊乱为主要临床特点。关于发作性睡病是否存在性别差异,不同的研究和报道给出了不同的结论。 一方面,从生理角度来看,男性和女性在…...

ppt从零基础到高手【办公】
第一章:文字排版篇01演示文稿内容基密02文字操作规范03文字排版处理04复习&作业解析第二章:图形图片图表篇05图形化表达06图片艺术化07轻松玩转图表08高效工具&母版统一管理09复习&作业解析10轻松一刻-文字图形小技巧速学第三章:…...

文件上传下载
文章目录 文件上传下载文件上传文件下载 文件上传下载 HTTP请求会包含一个请求头,其中"Content-Type"字段告诉服务器正在发送什么类型的数据。根据发送的数据类型,浏览器和服务器会采取适应的处理方式。 "multipart/form-data"是一…...

C++11 新特性:新增算法
C11 在标准库中引入了一系列新的算法,这些新增的算法使我们的代码写起来更简洁方便。 下面是 C11 中新增加的一些重要算法的简要描述和使用方法: 1、非修改序列操作 std::all_of:检查范围内的所有元素是否都满足指定的谓词。std::any_of&a…...
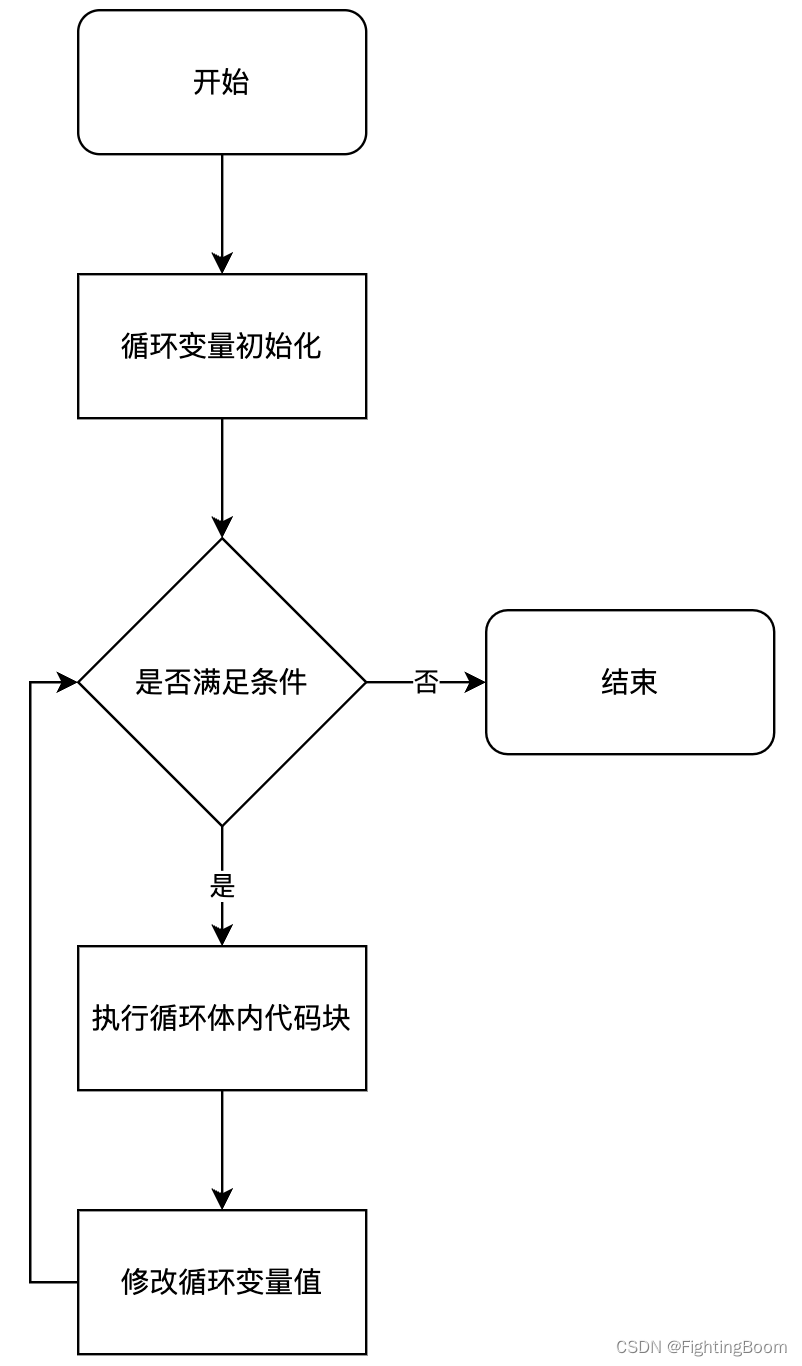
c/c++普通for循环学习
学习一下 for 循环的几种不同方式,了解一下原理及差异 完整的测试代码参考 GitHub :for 循环测试代码 1 常用形态 对于 for 循环来说,最常用的形态如下 for (表达式1; 表达式2; 表达式3) {// code }流程图如下: 编写测试代码…...
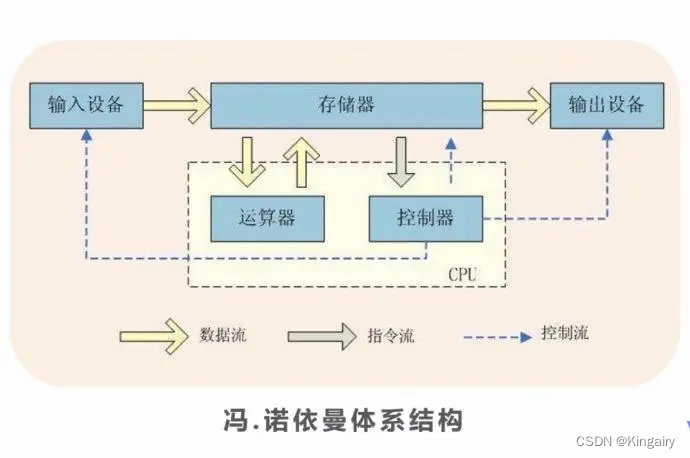
操作系统组成部分
从1946年诞生第一台电子计算机。 冯诺依曼结构 冯诺依曼是:数字计算机的数制采用二进制;计算机应该按照程序顺序执行。 常见的操作系统有三种类型 单用户单任务操作系统:只支持一个用户和一个任务的执行,如DOS;单用…...

深入理解DES算法:原理、实现与应用
title: 深入理解DES算法:原理、实现与应用 date: 2024/4/14 21:30:21 updated: 2024/4/14 21:30:21 tags: DES加密对称加密分组密码密钥管理S盒P盒安全性分析替代算法 DES算法简介 历史 DES(Data Encryption Standard)算法是由IBM研发&…...

# 达梦sql查询 Sql 优化
达梦sql查询 Sql 优化 文章目录 达梦sql查询 Sql 优化注意点测试数据单表查询 Sort 语句优化优化过程 多表关联SORT 优化函数索引的使用 注意点 关于优化过程中工具的选用,推荐使用自带的DM Manage,其它工具在查看执行计划等时候不明确在执行计划中命中…...

Linux下SPI驱动:SPI设备驱动简介
一. 简介 Linux下的SPI 驱动框架和 I2C 很类似,都分为主机控制器驱动和设备驱动,主机控制器也就是 SOC的 SPI 控制器接口,SPI设备驱动也就是所操作的SPI设备的驱动。 本文来学习一下Linux下SPI设备驱动。 二. Linux下SPI驱动:SP…...

【简明图文教程】Node.js的下载、安装、环境配置及测试
文章目录 前言下载Node.js安装Node.js配置Node.js配置环境变量测试后言 前言 本教程适用于小白第一次从零开始进行Node.js的下载、安装、环境配置及测试。 如果你之前已经安装过了Node.js或删除掉了Node.js想重新安装,需要先参考以下博客进行处理后,再根…...

共模电感饱和与哪些参数有关?这些参数是如何影响共模电感的?
在做一个变频器项目,遇到一个问题,在30Hz重载超过一定1小时,CE测试结果超出限制,查找原因最终发现EMI filter内的共模电感加热,fail现象可以复现。最终增大Y电容把问题解决了。由此问题引申出一个问题,到底…...
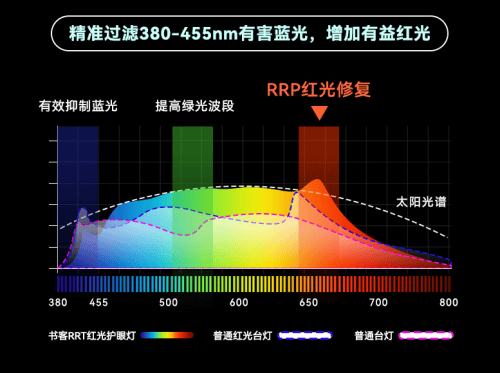
儿童护眼台灯怎么选?五款必选的高口碑护眼台灯推荐
儿童台灯,想必大家都不会陌生了,是一种学生频繁使用的小灯具,一般指放在桌面用的有底座的电灯。随着近年来儿童青少年的视力急速下滑,很多家长都会选择给孩子选择一款合适的护眼台灯,以便孩子夜晚学习能有个好的照明环…...

前端小技巧之轮播图
文章目录 功能htmlcssjavaScript图片 设置了一点小难度,不理解的话,是不能套用的哦!!! (下方的圆圈与图片数量不统一,而且宽度是固定的) 下次写一些直接套用的,不整这些麻…...
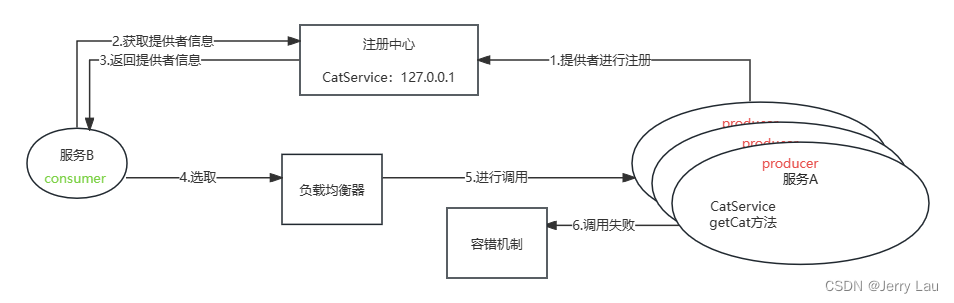
手动实现简易版RPC(上)
手动实现简易版RPC(上) 前言 什么是RPC?它的原理是什么?它有什么特点?如果让你实现一个RPC框架,你会如何是实现?带着这些问题,开始今天的学习。 本文主要介绍RPC概述以及一些关于RPC的知识,为…...
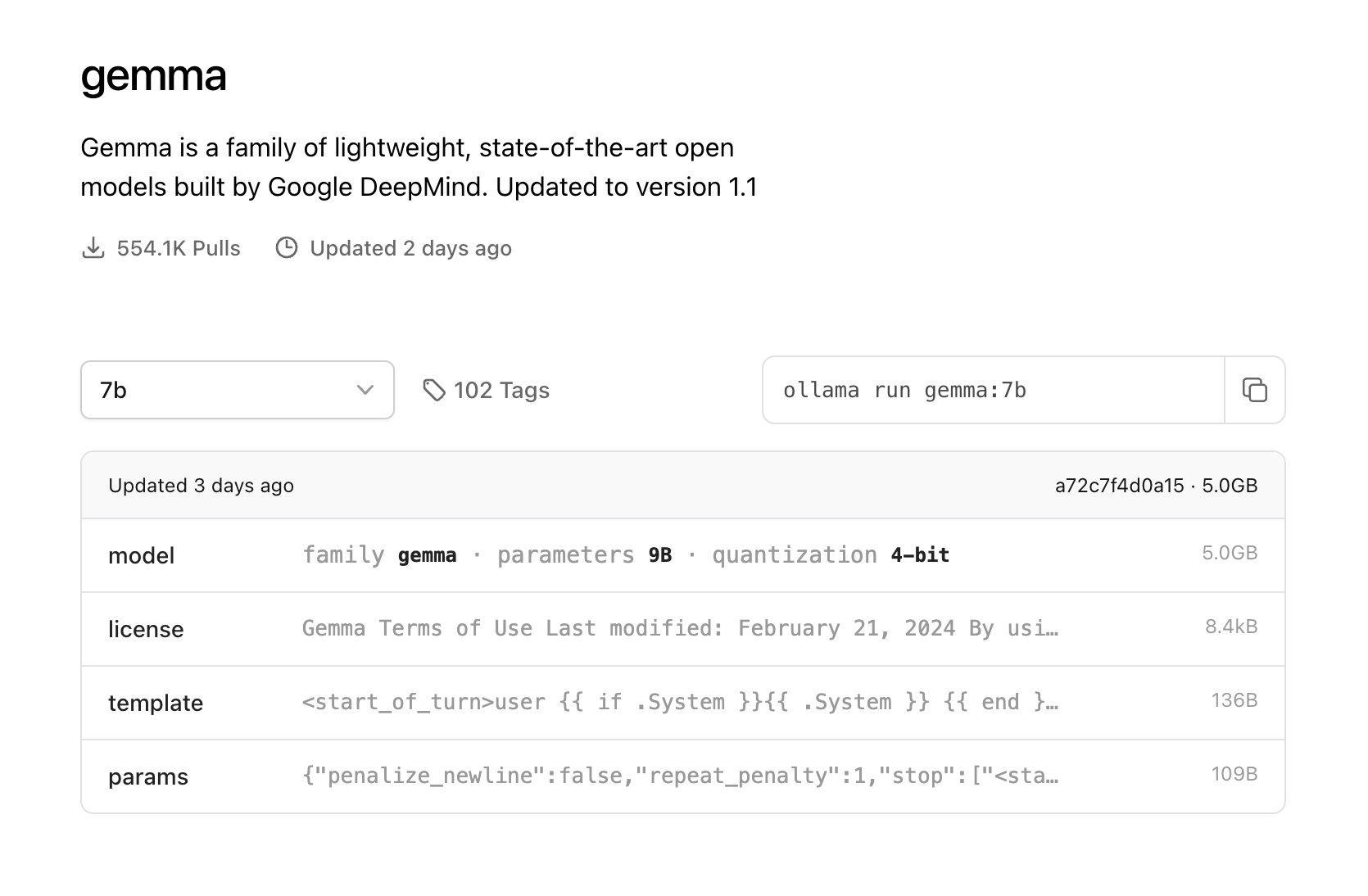
大语言模型总结整理(不定期更新)
《【快捷部署】016_Ollama(CPU only版)》 介绍了如何一键快捷部署Ollama,今天就来看一下受欢迎的模型。 模型简介gemmaGemma是由谷歌及其DeepMind团队开发的一个新的开放模型。参数:2B(1.6GB)、7Bÿ…...
)
关于npm和yarn的使用(自己的问题记录)
目录 一 npm 和 yarn 的区别 二 npm 和 yarn 常用命令对比 1. 初始化项目 2. 安装所有依赖包 3. 安装某个依赖包 4.安装某个版本的依赖包 5. 更新依赖包 5. 移除依赖包 三 package.json中 devDependencies 和 dependencies 的区别。 四 npm安装包时,…...
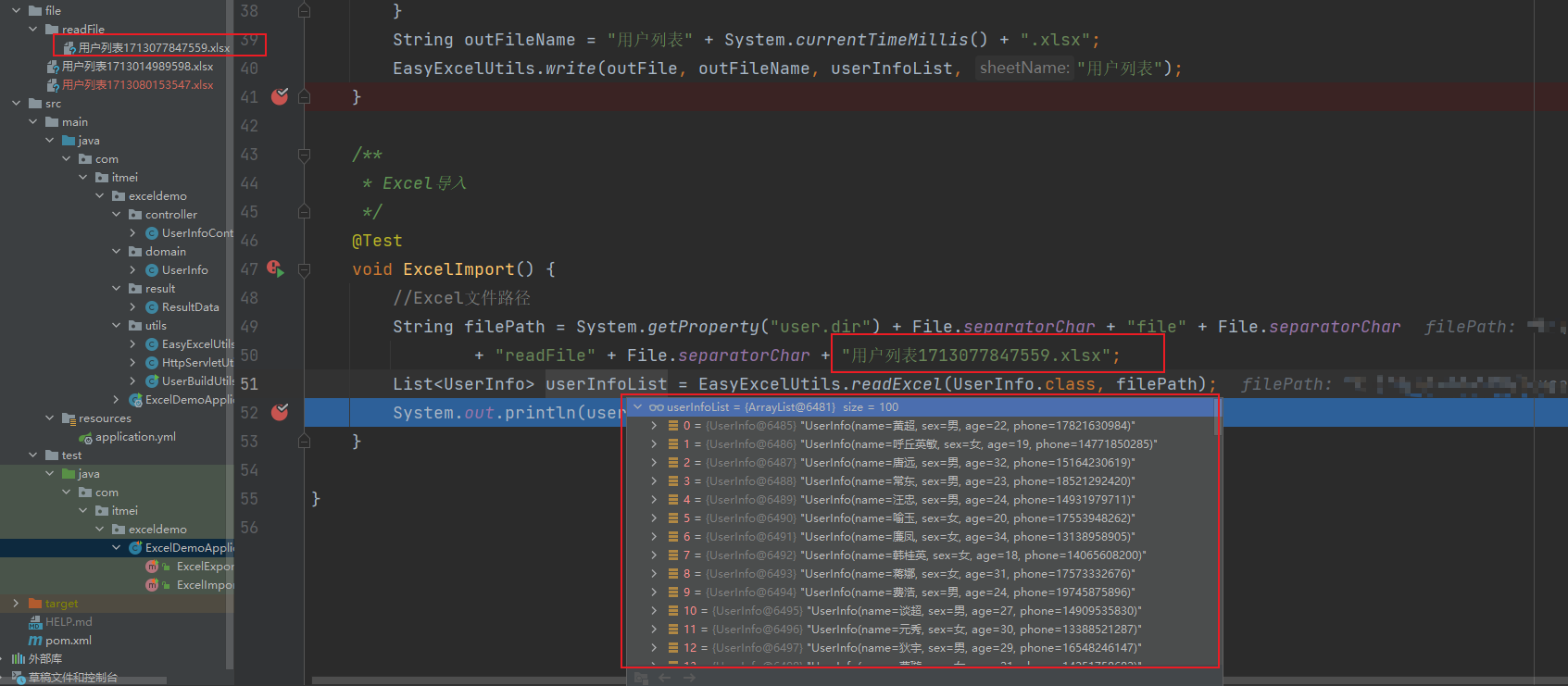
Web端Excel的导入导出Demo
📚目录 📚简介:✨代码的构建:💭Web端接口Excel操作🚀下载接口🚀导入读取数据接口 🏡本地Excel文件操作⚡导出数据🌈导入读取数据 📚简介: 使用阿里巴巴开源组件Easy Exce…...
Java日期正则表达式(附Demo)
目录 前言1. 基本知识2. Demo 前言 对于正则匹配,在项目实战中运用比较广泛 原先写过一版Python相关的:ip和端口号的正则表达式 1. 基本知识 对于日期的正则相对比较简单 以下是一些常见的日期格式及其对应的正则表达式示例: 年-月-日&a…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...

c# 局部函数 定义、功能与示例
C# 局部函数:定义、功能与示例 1. 定义与功能 局部函数(Local Function)是嵌套在另一个方法内部的私有方法,仅在包含它的方法内可见。 • 作用:封装仅用于当前方法的逻辑,避免污染类作用域,提升…...

Xela矩阵三轴触觉传感器的工作原理解析与应用场景
Xela矩阵三轴触觉传感器通过先进技术模拟人类触觉感知,帮助设备实现精确的力测量与位移监测。其核心功能基于磁性三维力测量与空间位移测量,能够捕捉多维触觉信息。该传感器的设计不仅提升了触觉感知的精度,还为机器人、医疗设备和制造业的智…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

企业大模型服务合规指南:深度解析备案与登记制度
伴随AI技术的爆炸式发展,尤其是大模型(LLM)在各行各业的深度应用和整合,企业利用AI技术提升效率、创新服务的步伐不断加快。无论是像DeepSeek这样的前沿技术提供者,还是积极拥抱AI转型的传统企业,在面向公众…...

GAN模式奔溃的探讨论文综述(一)
简介 简介:今天带来一篇关于GAN的,对于模式奔溃的一个探讨的一个问题,帮助大家更好的解决训练中遇到的一个难题。 论文题目:An in-depth review and analysis of mode collapse in GAN 期刊:Machine Learning 链接:...

SQL注入篇-sqlmap的配置和使用
在之前的皮卡丘靶场第五期SQL注入的内容中我们谈到了sqlmap,但是由于很多朋友看不了解命令行格式,所以是纯手动获取数据库信息的 接下来我们就用sqlmap来进行皮卡丘靶场的sql注入学习,链接:https://wwhc.lanzoue.com/ifJY32ybh6vc…...
