LoRA微调
论文:LoRA: Low-Rank Adaptation of Large Language Models
实现:microsoft/LoRA: Code for loralib, an implementation of “LoRA: Low-Rank Adaptation of Large Language Models” (github.com)
摘要
自然语言处理的一个重要的开发范式包括:
- 对通用领域数据进行大规模的预训练;
- 对特定任务或领域的适应。
问题:当预训练的模型越来越大,全参数的微调(full fine-tuning)变得比较困难了。
解决方法:Low-Rank Adaptation,简称LoRA,其冻结了预训练的模型权重,并将可训练的秩分解矩阵注入Transformer架构的每一层,大大减少了下游任务的可训练参数的数量。
简介
[1804.08838] Measuring the Intrinsic Dimension of Objective Landscapes
上述文章表明,学习到的过度参数化模型权重实际上存在于一个较低的内在维度空间上。我们假设模型适应过程中权重的变化也具有较低的“内在秩”(也就是只在内在的低维空间中变化),从而提出了低秩适应(LoRA)方法。LoRA允许我们通过优化适应过程中密集层变化的秩分解矩阵,间接地训练神经网络中的一些密集层,同时冻结预训练权重:

LoRA有几个关键的优势:
- 一个预训练模型可以被共享,并用于为不同的任务构建许多小型的LoRA模块。我们可以通过替换低秩适应示意图中的矩阵A和矩阵B来冻结共享模型并有效地切换任务,从而显著地减少了存储需求和任务切换开销。
- 当使用自适应优化器时,LoRA使训练更高效,并将硬件准入门槛降低了3倍,因为我们不需要为大多数的参数计算梯度或维护其优化器状态。相反,我们只需要优化注入的、小得多的低秩矩阵。
- 我们简单的线性设计允许我们在部署时通过构造将可训练矩阵与冻结权重合并,与完全微调的模型相比,不会引入推理延迟。
- LoRA与许多先前的方法互不影响,并且可以与其中的许多方法结合起来,比如前缀调优(prefix-tuning)。
问题陈述
LoRA并不特定于某个具体的训练目标,这里以语言建模(language modeling)问题为用例进行问题描述。
给定一个以 Φ \Phi Φ为参数的预训练自回归语言模型 P Φ ( y ∣ x ) P_\Phi(y|x) PΦ(y∣x)。比如, P Φ ( y ∣ x ) P_\Phi(y|x) PΦ(y∣x)可以是一个像GPT一样的基于Transformer的通用多任务学习器。考虑将这个预训练模型适应于下游的条件文本生成任务,如摘要、机器阅读理解(MRC)和自然语言转SQL(NL2SQL)。每个下游任务都由一个上下文-目标对训练数据集表示: Z = { ( x i , y i ) } i = 1 , . . . , N \mathcal{Z}=\{(x_i,y_i)\}_{i=1,...,N} Z={(xi,yi)}i=1,...,N,其中 x i x_i xi和 y i y_i yi是token序列。例如,在NL2SQL中, x i x_i xi是一个自然语言查询, y i y_i yi是它对应的SQL命令;对于摘要, x i x_i xi是一篇文章的内容, y i y_i yi是它的摘要。
在全微调过程中,模型被初始化为预训练权重 Φ 0 \Phi_0 Φ0,并通过不断累积梯度最终更新为 Φ 0 + Δ Φ \Phi_0 + \Delta\Phi Φ0+ΔΦ,以最大化条件语言建模目标函数:
max Φ ∑ ( x , y ) ∈ Z ∑ t = 1 ∣ y ∣ log ( P Φ ( y t ∣ x , y < t ) ) \max _{\Phi} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log \left(P_{\Phi}\left(y_{t} \mid x, y_{<t}\right)\right) Φmax(x,y)∈Z∑t=1∑∣y∣log(PΦ(yt∣x,y<t))
全微调的一个主要缺点是,对于每个下游任务,都需要学习了一组不同的参数 Δ Φ \Delta\Phi ΔΦ,其维数 ∣ Δ Φ ∣ |\Delta\Phi| ∣ΔΦ∣等于 ∣ Φ 0 ∣ |\Phi_0| ∣Φ0∣。因此,如果预训练模型很大(比如175B的GPT-3),那么存储和部署许多独立的微调模型实例各方面的开销和压力会比较大。
本文采用了一种更加参数高效(parameter-efficient)的方法,将任务特定的参数增量 Δ Φ = Δ Φ ( Θ ) \Delta\Phi=\Delta\Phi\left(\Theta\right) ΔΦ=ΔΦ(Θ)进一步用小得多的参数集 Θ \Theta Θ进行编码,其中 ∣ Θ ∣ ≪ ∣ Φ 0 ∣ |\Theta| \ll |\Phi_0| ∣Θ∣≪∣Φ0∣。所以,寻找 Δ Φ \Delta\Phi ΔΦ的任务变成了对 Θ \Theta Θ的优化:
max Θ ∑ ( x , y ) ∈ Z ∑ t = 1 ∣ y ∣ log ( P Φ 0 + Δ Φ ( Θ ) ( y t ∣ x , y < t ) ) \max _{\Theta} \sum_{(x, y) \in \mathcal{Z}} \sum_{t=1}^{|y|} \log \left(P_{\Phi_0 + \Delta\Phi(\Theta)}\left(y_{t} \mid x, y_{<t}\right)\right) Θmax(x,y)∈Z∑t=1∑∣y∣log(PΦ0+ΔΦ(Θ)(yt∣x,y<t))
现有方法存在的问题
两种高效适应下游任务的策略:
- 添加适配器层
- 对输入层做某种形式的优化
存在的问题:
- 适配器层引入了推理延迟
- 直接优化提示是困难的
本文的方法
虽然本文中只关注Transformer语言模型中的某些权重作为用例,但该方法适用于深度学习模型中的任何密集层。
低秩参数化更新矩阵(LOW-RANK-PARAMETRIZED UPDATE MATRICES)
当适应一个特定的任务时,论文Intrinsic Dimensionality Explains the Effectiveness of Language Model Fine-Tuning表明了预训练语言模型具有较低的“内在维度”,尽管随机投影到更小的子空间,但仍然可以有效地学习。受此启发,做出假设:在适应下游任务的过程中,权重的更新也有一个较低的“内在秩”。对于预训练的权重矩阵 W 0 ∈ R d × k W_0 \in \mathbb{R}^{d \times k} W0∈Rd×k,使用低秩分解 W 0 + Δ W = W 0 + B A W_0+\Delta W = W_0+BA W0+ΔW=W0+BA表示后者来约束其更新,其中 B ∈ R d × r B \in \mathbb{R}^{d \times r} B∈Rd×r, A ∈ R r × k A \in \mathbb{R}^{r \times k} A∈Rr×k和秩 r ≪ min ( d , k ) r \ll \min(d,k) r≪min(d,k)。
在微调过程中, W 0 W_0 W0被冻结,不接收梯度更新,而 A A A和 B B B包含可训练的参数。 W 0 W_0 W0和 Δ W = B A \Delta W = BA ΔW=BA都与相同的输入相乘,它们各自的输出向量按坐标求和。
对于 h = W 0 x h = W_0x h=W0x,修改后的正向传播为:
h = W 0 x + Δ W x = W 0 x + B A x h = W_0x + \Delta Wx = W_0x + BAx h=W0x+ΔWx=W0x+BAx
可训练参数的初始化:
- A A A:随机高斯
- B B B:0
所以 Δ W = B A \Delta W = BA ΔW=BA在训练开始时为零。
We then scale Δ W x \Delta Wx ΔWx by α r \frac{\alpha}{r} rα, where α \alpha α is a constant in r r r. When optimizing with Adam, tuning α \alpha α is roughly the same as tuning the learning rate if we scale the initialization appropriately. As a result, we simply set α \alpha α to the first r r r we try and do not tune it. This scaling helps to reduce the need to retune hyperparameters when we vary r r r.
-
A Generalization of Full Fine-tuning
一种更一般的微调形式允许训练预训练参数的一个子集。LoRA更进一步,不需要权重矩阵的累积梯度更新在适应过程中具有全秩。这意味着,当将LoRA应用于所有权重矩阵并训练所有偏置项时,通过将LoRA的秩 r r r设置为预训练权重矩阵的秩,可以大致恢复完全微调的表达性。换句话说,当增加可训练参数的数量时,训练LoRA将大致收敛为训练原始模型,而基于适配器的方法和基于前缀的方法则分别收敛到一个MLP和一个不能接受长输入序列的模型。
-
No Additional Inference Latency
当在生产环境中部署时,可以显式地计算和存储任务特定的权重 W = W 0 + B A W = W_0 + BA W=W0+BA,然后将该权重加载进模型并像往常一样执行推理。注意 W 0 W_0 W0和 B A BA BA都在 R d × k \mathbb{R}^{d \times k} Rd×k中。当需要切换到另一个下游任务时,可以通过减去 B A BA BA来恢复 W 0 W_0 W0,然后加上一个不同的 B ′ A ′ B^{\prime}A^{\prime} B′A′,这是一个快速的内存开销很少的操作。重要的是,这确保了与通过构造进行微调的模型相比,这种方式在推理过程中没有引入任何额外的延迟。
在Transformer上应用LoRA
原则上,LoRA可以应用于神经网络中的权重矩阵的任何子集,以减少可训练参数的数量。在Transformer架构中,自注意模块中有四个权重矩阵( W q W_q Wq、 W k W_k Wk、 W v W_v Wv、 W o W_o Wo),在MLP模块中有两个。我们将 W q W_q Wq(或 W k W_k Wk, W v W_v Wv)视为一个形状为 d m o d e l × d m o d e l d_{model} \times d_{model} dmodel×dmodel的单一矩阵,即使输出维通常被切分成注意力头。

实际的获益和局限性
获益
- 最显著的好处来自于内存和存储使用量的减少。对于使用Adam训练的大型Transformer网络,如果 r ≪ d m o d e l r \ll d_{model} r≪dmodel,则VRAM使用量减少 2 / 3 2/3 2/3,因为不需要存储冻结参数的优化器状态。在GPT-3 175B上,训练期间的VRAM消耗从1.2TB减少到350GB。当 r = 4 r = 4 r=4和只对Query和Value投影矩阵进行调整时,检查点的大小减少了大约10000倍(从350GB减少到35MB)。这让我们可以使用少得多的gpu进行训练,并极大地避免I/O瓶颈。
- 另一个好处是,通过只切换LoRA的权重,而不是所有的参数,可以在部署后以低得多的开销在不同任务间切换。
- 我们还观察到,与完全微调相比,在GPT-3 175B上的训练速度提高了25%,因为不需要计算绝大多数参数的梯度。
局限性
例如,如果选择将 A A A和 B B B吸收到 W W W中以消除额外的推理延迟,那么在单次正向传递中批量处理具有不同 A A A和 B B B的不同任务的输入是很难的。尽管在延迟不是很重要的情况下,可以不合并权重并动态选择用于批处理中的样本的LoRA模块。
理解低秩更新
作者进行了一系列的实证研究来回答以下问题:
- 给定一个参数预算约束,在预训练的Transformer网络中应该适应权重矩阵的哪个子集以最大化下游性能?
- “最优”的适应矩阵 Δ W \Delta W ΔW真的是秩亏的吗?如果是这样,在实践中使用什么秩比较好?
- Δ W \Delta W ΔW和 W W W之间有什么关系? Δ W \Delta W ΔW与 W W W高度相关吗?与 W W W相比, Δ W \Delta W ΔW有多大?
我们应该将LORA应用到Transformer中的哪些权重矩阵?
给定有限的参数预算,应该使用LoRA调整哪些类型的权重才能在下游任务上获得最佳性能?这里只考虑自注意力模块中的权重矩阵。在GPT-3 175B上设置了18M的参数预算(如果以FP16存储,大约为35MB),对于所有96层,如果适应一种类型的注意力权重,则对应于 r = 8 r = 8 r=8;如果适应两种类型,则对应于 r = 4 r = 4 r=4。以下是实验结果:

可以看到,将所有参数放入 Δ W q \Delta W_q ΔWq或 Δ W k \Delta W_k ΔWk会导致性能显著降低,而同时调整 W q W_q Wq和 W v W_v Wv会产生最佳结果。这表明,即使是值为4的秩也能捕获 Δ W \Delta W ΔW中足够的信息,因此适应更多的权重矩阵比使用更大的秩适应单一类型的权重更好。
对于LoRA最优的秩 r r r是什么

可以看出,使用一个非常小的 r r r就足以让LoRA表现得很好了,这表明更新矩阵 Δ W \Delta W ΔW可能有一个非常小的“内在秩”。但是不能指望一个小的 r r r适用于每个任务或数据集。假设下游任务使用的语言与预训练所使用的语言不同,则重新训练整个模型(类似于 r = d m o d e l r = d_{model} r=dmodel的LoRA)肯定会优于 r r r较小的LoRA。为了进一步支持这一发现,作者检查了使用不同的 r r r和不同随机种子学习到的子空间的重叠情况,得出结论:增加 r r r不覆盖一个更有意义的子空间,这表明一个低秩适应矩阵是足够的。
适应矩阵 Δ W \Delta W ΔW与 W W W相比如何?
通过计算 U T W V T U^{\mathsf{T}}WV^{\mathsf{T}} UTWVT将 W W W投影到 Δ W \Delta W ΔW的 r r r维子空间上,其中 U U U/ V V V是 Δ W \Delta W ΔW的左/右奇异向量矩阵,然后计算相应的Frobenius norm。作为比较,我们还将 U U U、 V V V替换为 W W W或一个随机矩阵的前 r r r个奇异向量后计算 ∥ U T W V T ∥ F \parallel U^{\mathsf{T}}WV^{\mathsf{T}}\parallel_F ∥UTWVT∥F的值。结果如下:

从上表可以得出几个结论:
- 与随机矩阵相比, Δ W \Delta W ΔW与 W W W有更强的相关性,这表明 Δ W \Delta W ΔW放大了 W W W中已经存在的一些特征。
- Δ W \Delta W ΔW没有重复 W W W靠前的奇异向量方向,而是只放大了 W W W中没有强调的方向。
- 放大系数相当大:当 r = 4 r=4 r=4时,为 21.5 ≈ 6.91 / 0.32 21.5 \approx 6.91/0.32 21.5≈6.91/0.32
这表明,低秩适应矩阵潜在地放大了特定下游任务的重要特征,这些特征是通用预训练模型学习到但并未注重的。
相关文章:

LoRA微调
论文:LoRA: Low-Rank Adaptation of Large Language Models 实现:microsoft/LoRA: Code for loralib, an implementation of “LoRA: Low-Rank Adaptation of Large Language Models” (github.com) 摘要 自然语言处理的一个重要的开发范式包括&#…...
45.基于SpringBoot + Vue实现的前后端分离-驾校预约学习系统(项目 + 论文)
项目介绍 本站是一个B/S模式系统,采用SpringBoot Vue框架,MYSQL数据库设计开发,充分保证系统的稳定性。系统具有界面清晰、操作简单,功能齐全的特点,使得基于SpringBoot Vue技术的驾校预约学习系统设计与实现管理工作…...

系统思考—时间滞延
“没有足够的时间是所有管理问题的一部分。”——彼得德鲁克 鱼和熊掌可以兼得,但并不能同时获得。在提出系统解决方案时,我们必须认识到并考虑到解决方案的实施通常会有必要的时间滞延。这种延迟有时比我们预想的要长得多,特别是当方案涉及…...

SSM项目转Springboot项目
SSM项目转Springboot项目 由于几年前写的一个ssm项目想转成springboot项目,所以今天倒腾了一下。 最近有人需要毕业设计转换一下,所以我有时间的话可以有偿帮忙转换,需要的私信我或+v:Arousala_ 首先创建一个新的spr…...

VUE3.0对比VUE2.0
vue3.0 与 vue2.0的不同之处有以下几点: 数据响应式原理 3.0基于Proxy的代理实现监测,vue2.0是基于Object.defineProperty实现监测。 vue2.0 通过Object.defineProperty,每个数据属性被定义成可观察的,具有getter和setter方法&…...
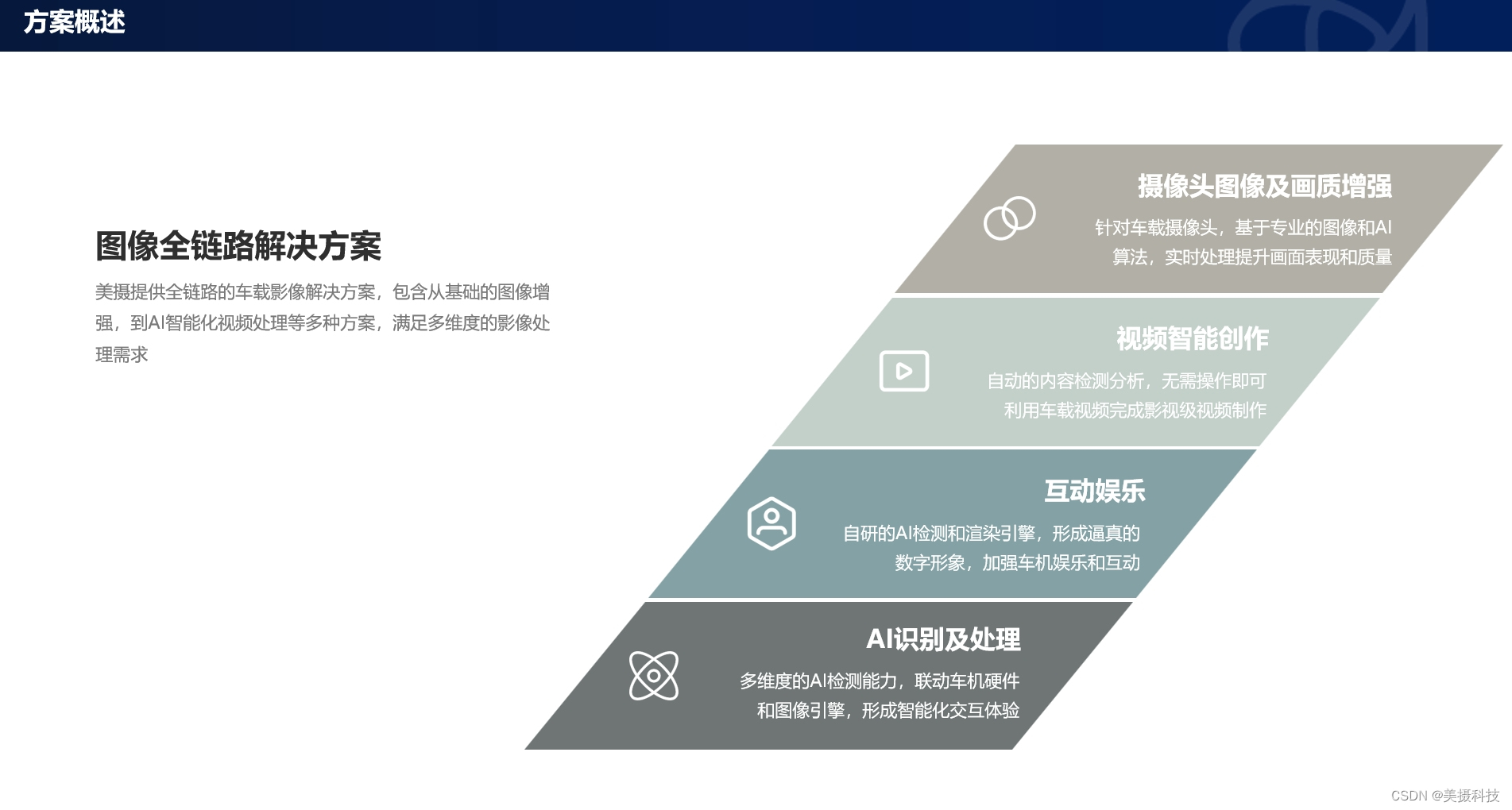
车内AR互动娱乐解决方案,打造沉浸式智能座舱体验
美摄科技凭借其卓越的创新能力,为企业带来了革命性的车内AR互动娱乐解决方案。该方案凭借自研的AI检测和渲染引擎,打造出逼真的数字形象,不仅丰富了车机娱乐内容,更提升了乘客与车辆的互动体验,让每一次出行都成为一场…...

OR36 链表的回文结构
描述 对于一个链表,请设计一个时间复杂度为O(n),额外空间复杂度为O(1)的算法,判断其是否为回文结构。 给定一个链表的头指针A,请返回一个bool值,代表其是否为回文结构。保证链表长度小于等于900。 测试样例: 1->…...

【译】微调与人工引导: 语言模型调整中的 SFT 和 RLHF
原文地址:Fine-Tuning vs. Human Guidance: SFT and RLHF in Language Model Tuning 本文主要对监督微调(SFT, Supervised Fine Tuning )和人类反馈强化学习(RLHF, Reinforcement Learning from Human Feedback)进行简…...
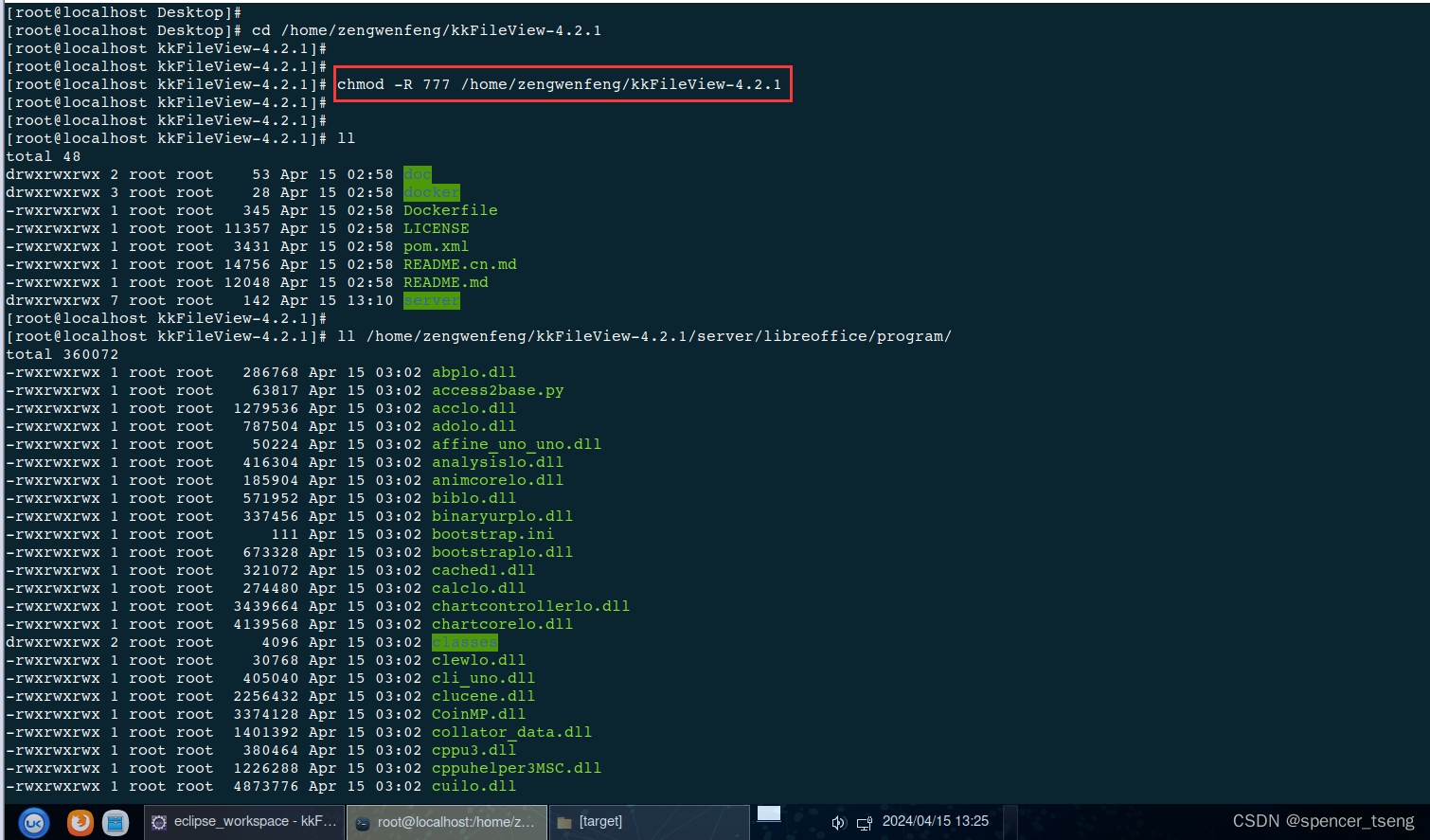
kylin java.io.IOException: error=13, Permission denied
linux centos7.8 error13, Permission denied_linux open error13-CSDN博客 chmod -R 777 /home/zengwenfeng/kkFileView-4.2.1 2024-04-15 13:15:17.416 WARN 3400 --- [er-offprocmng-1] o.j.l.office.LocalOfficeProcessManager : An I/O error prevents us to determine…...

前端面试01总结
1.Js 中!x为true 时,x可能为哪些值 答: 1.false:布尔值false 2.0或-0:数字零 3.""或’或 (空字符串):长度为0的字符串 4.null:表示没有任何值的特殊值 5.undefined:变量未定义时的默认…...

算法--目录
algorithm: 十种排序算法 二分法-各种应用 algorithm: 拓扑排序 算法中的背包问题 最长子序列问题 前缀和-解题集合 差分数组-解题...
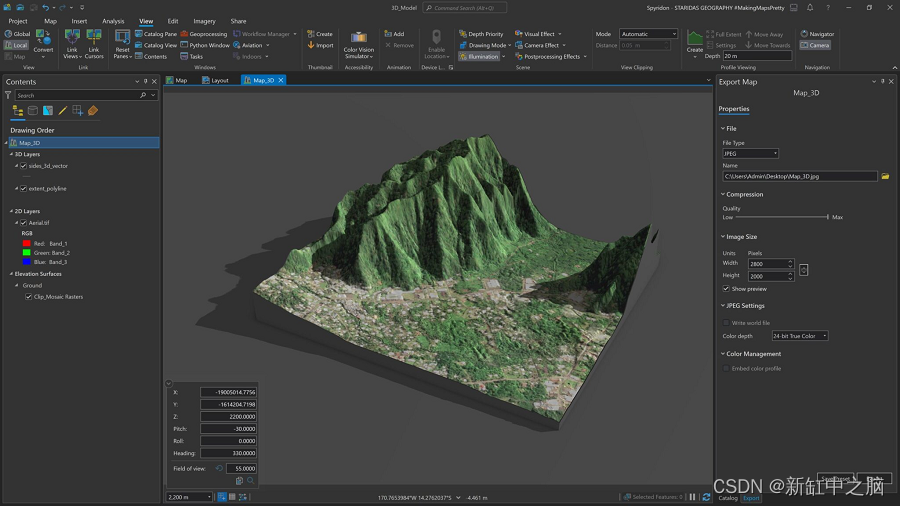
ArcGIS Pro 3D建模简明教程
在本文中,我讲述了我最近一直在探索的在 ArcGIS Pro 中设计 3D 模型的过程。 我的目标是尽可能避免与其他软件交互(即使是专门用于 3D 建模的软件),并利用 Pro 可以提供的可能性。 这个短暂的旅程分为三个不同的阶段:…...

24届数字IC设计/验证秋招总结贴——先看这个
文章目录 前言一、经验篇二、知识学习篇三、笔试篇3.1 各大公司笔试真题3.2 华为机试——数字芯片笔试题汇总 四、面试篇4.1 时间节点4.2 提前批4.3 正式批 前言 为方便快速进行查找该专栏的内容,将所有内容链接均放在此篇博客中 整理不易,欢迎订阅~~ …...
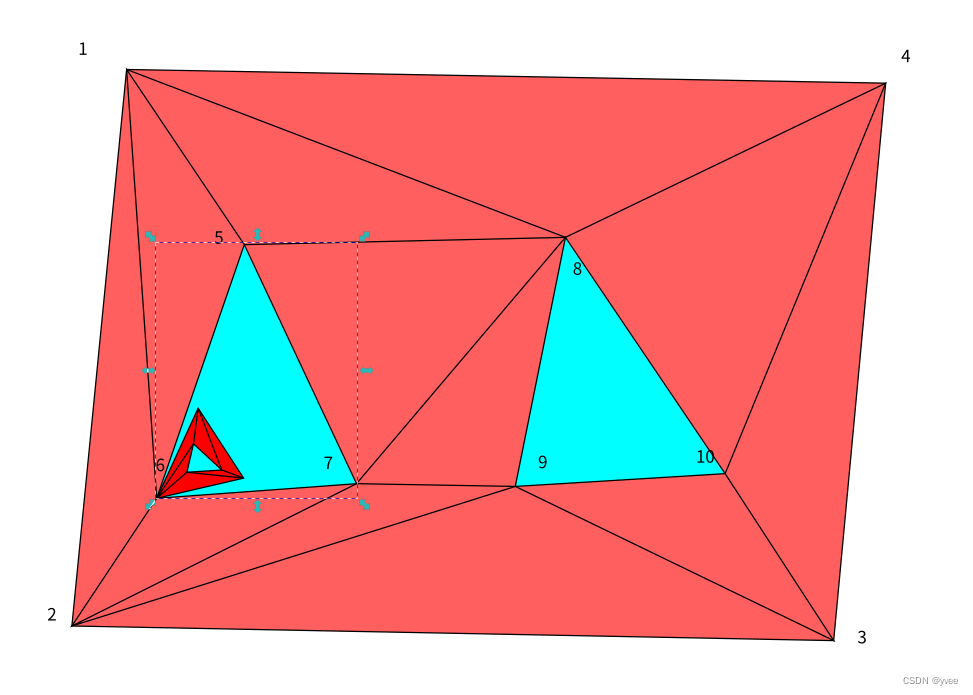
带洞平面三角分割结果的逆向算法
先标不重复点,按最近逐个插入。 只说原理。 不带洞的 1 2 4 2 3 4 两个三角形 结果 1 2 3 4 无重复 无洞 1 2 6 1 2 3 6 1 2 3 7 6 1 2 3 4 7 6 1 2 3 4 5 7 6 1 2 3 4 1 5 7 6 1 2 3 4 1 6 5 7 6 最终结果 1 2 3 4 1 6 5 7 6 按重复分割 1 2 3…...

MGRE-OSPF接口网络类型实验
OSPF接口网络类型实验 一,实验拓扑 初始拓扑: 最终拓扑: 二,实验要求及分析 要求: 1,R6为ISP只能配置IP地址,R1-R5的环回为私有网段 2,R1/R4/R5为全连的MGRE结构,R…...

ChatGPT科研利器详解:写作论文轻松如玩游戏
ChatGPT无限次数:点击直达 ChatGPT科研利器详解:写作论文轻松如玩游戏 引言 在当今科技日新月异的时代,人工智能技术的应用越来越广泛,其中自然语言处理领域的发展尤为迅猛。ChatGPT作为一款先进的文本生成模型,为科研工作者提供…...

vue3从精通到入门23:定义全局变量
在vue2中,我们知道vue2.x是使用Vue.prototype.$xxxxxxx来定义全局变量, 比如定义一个全局的工具函数。 // 定义 ... Vue.prototype.$utilsutils;// 使用 this.$utils() ... 在vue3中我们无法使用this,提供了globalProperties; …...
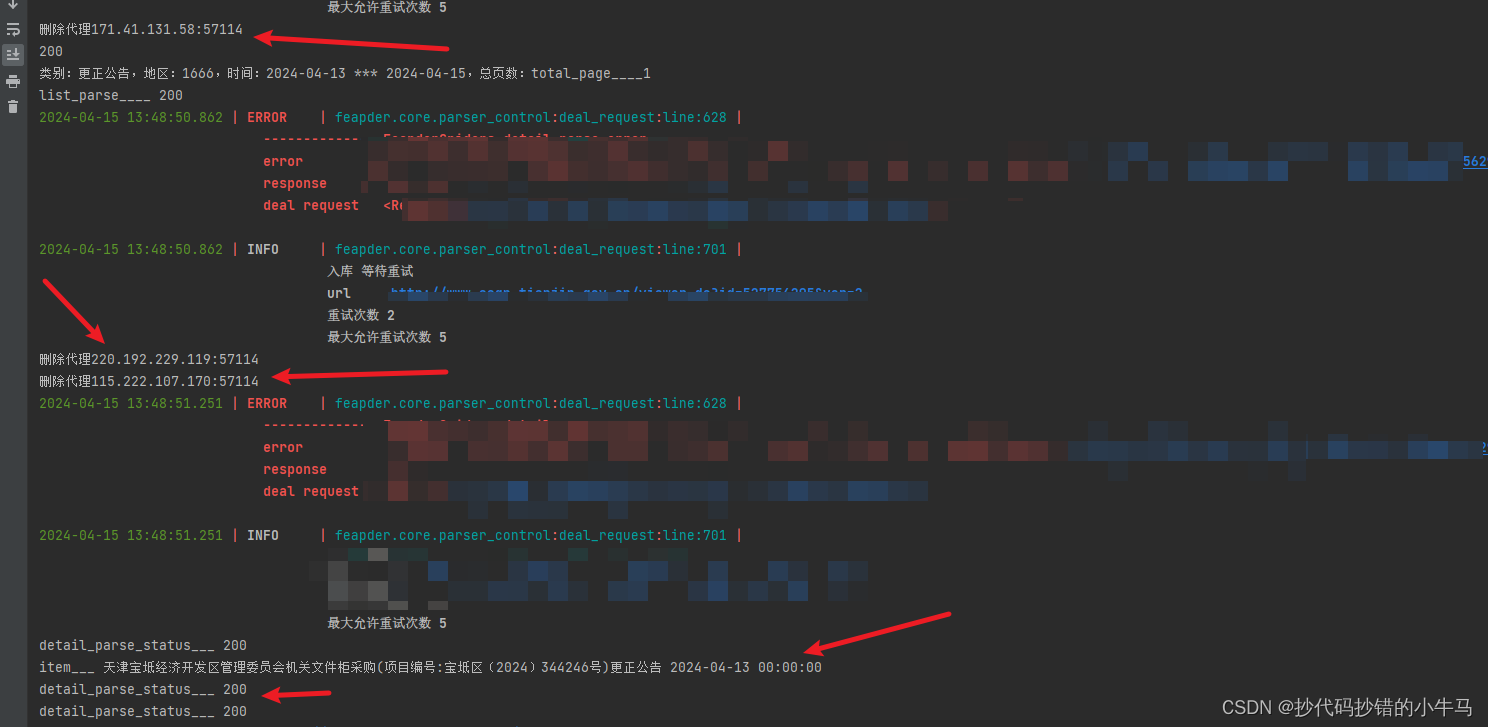
反爬虫之代理IP封禁-协采云IP池
反爬虫之代理IP封禁-协采云IP池 1、目标网址2、IP封禁4033、协采云IP池 1、目标网址 aHR0cDovL3d3dy5jY2dwLXRpYW5qaW4uZ292LmNuLw 2、IP封禁403 这个网站对IP的要求很高,短时间请求十几次就会遭关进小黑屋。如下图: 明显是网站进行了反爬处理&…...
ELK-Kibana 部署
目录 一、在 node1 节点上操作 1.1.安装 Kibana 1.2.设置 Kibana 的主配置文件 1.3.启动 Kibana 服务 1.4.验证 Kibana 1.5.将 Apache 服务器的日志(访问的、错误的)添加到 ES 并通过 Kibana 显示 1.6. 浏览器访问 二、部署FilebeatELK&…...
——在jupyter中执行bt的samples)
Backtrader 量化回测实践(7)——在jupyter中执行bt的samples
Backtrader 量化回测实践(7)——在jupyter中执行bt的samples Backtrader提供了大量的测试用例,在samples目录下,测试程序主要都是用argparse解析参数,但是不能在jupyter中直接执行。 找到一个解决方法,可…...
)
浏览器访问 AWS ECS 上部署的 Docker 容器(监听 80 端口)
✅ 一、ECS 服务配置 Dockerfile 确保监听 80 端口 EXPOSE 80 CMD ["nginx", "-g", "daemon off;"]或 EXPOSE 80 CMD ["python3", "-m", "http.server", "80"]任务定义(Task Definition&…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

基础测试工具使用经验
背景 vtune,perf, nsight system等基础测试工具,都是用过的,但是没有记录,都逐渐忘了。所以写这篇博客总结记录一下,只要以后发现新的用法,就记得来编辑补充一下 perf 比较基础的用法: 先改这…...

华为OD机试-食堂供餐-二分法
import java.util.Arrays; import java.util.Scanner;public class DemoTest3 {public static void main(String[] args) {Scanner in new Scanner(System.in);// 注意 hasNext 和 hasNextLine 的区别while (in.hasNextLine()) { // 注意 while 处理多个 caseint a in.nextIn…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

【7色560页】职场可视化逻辑图高级数据分析PPT模版
7种色调职场工作汇报PPT,橙蓝、黑红、红蓝、蓝橙灰、浅蓝、浅绿、深蓝七种色调模版 【7色560页】职场可视化逻辑图高级数据分析PPT模版:职场可视化逻辑图分析PPT模版https://pan.quark.cn/s/78aeabbd92d1...

SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候,发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升,且低水位伴随在整个慢 SQL,一直是 buferIO 的等待事件,此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ,但…...
