OpenCV轻松入门(八)——图片卷积
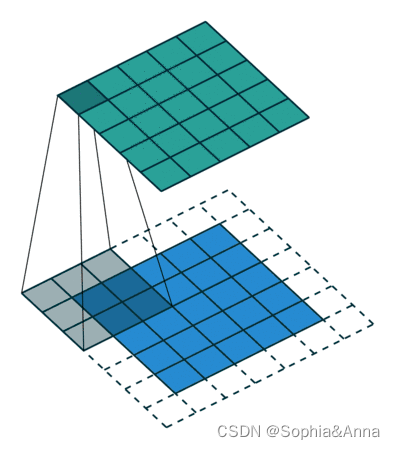
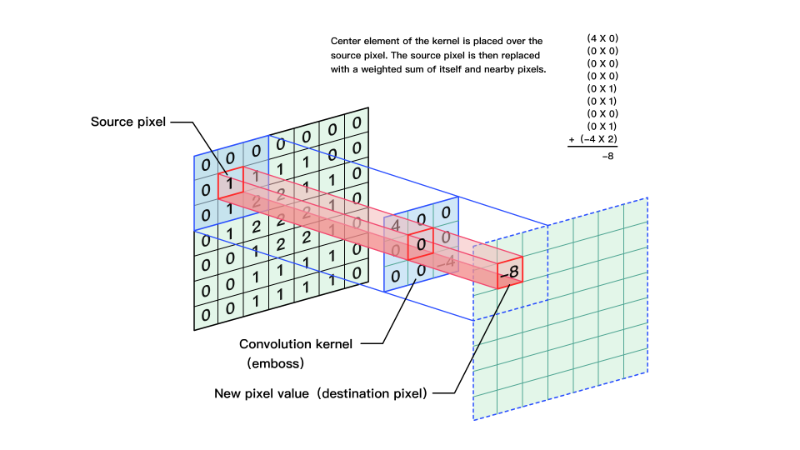
对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置,这个操作就叫卷积。
卷积需要4个嵌套循环,所以它并不快,除非我们使用很小的卷积核。这里一般使用3x3或者5x5
图像滤波
图像滤波是尽量保留图像细节特征的条件下对目标图像的噪声进行抑制,是图像预处理中不可缺少的操作,其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。
线性滤波是图像处理最基本的方法,它允许我们对图像进行处理,产生很多不同的效果。首先,我们需要一个二维的滤波器矩阵(卷积核)和一个要处理的二维图像。然后,对于图像的每一个像素点,计算它的邻域像素和滤波器矩阵的对应元素的乘积,然后加起来,作为该像素位置的值。这样就完成了滤波过程。
对于滤波器/卷积核,也有一定的规则要求:
- 滤波器的大小应该是奇数,这样它才有一个中心,例如3x3,5x5或者7x7。有中心了,也有了半径的称呼,例如5x5大小的核的半径就是2
- 滤波器矩阵所有的元素之和应该要等于1,这是为了保证滤波前后图像的亮度保持不变。当然了,这不是硬性要求了。
- 如果滤波器矩阵所有元素之和大于1,那么滤波后的图像就会比原图像更亮,反之,如果小于1,那么得到的图像就会变暗。如果和为0,图像不会变黑,但也会非常暗。
- 对于滤波后的结构,可能会出现负数或者大于255的数值。对这种情况,我们将他们直接截断到0和255之间即可。对于负数,也可以取绝对值。
均值滤波
将卷积核内的所有灰度值加起来,然后计算出平均值,用这个平均值填充卷积核正中间的值,这样做可以降低图像的噪声,同时也会导致图像变得模糊。
代码实现
import cv2
import numpy as np
import matplotlib.pyplot as plt# 写代码时用的jupyter,cv2.imshow总是卡死,所以用的plt方便显示图像
def imgshow(img):img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)plt.imshow(img)plt.show()dog_img = cv2.imread('/Users/guojun/Desktop/444.png',cv2.IMREAD_COLOR)
# 均值滤波: cv2.blur(img,knelsize) img-图片,卷积核大小
dst = cv2.blur(dog_img,(10,10))
imgshow(dst)高斯模糊
采用均值滤波降噪会导致图像模糊的非常厉害,有没有一种方式既能保留像素点真实值又能降低图片噪声呢?那就是加权平均的方式. 离中心点越近权值越高,越远权值越低.
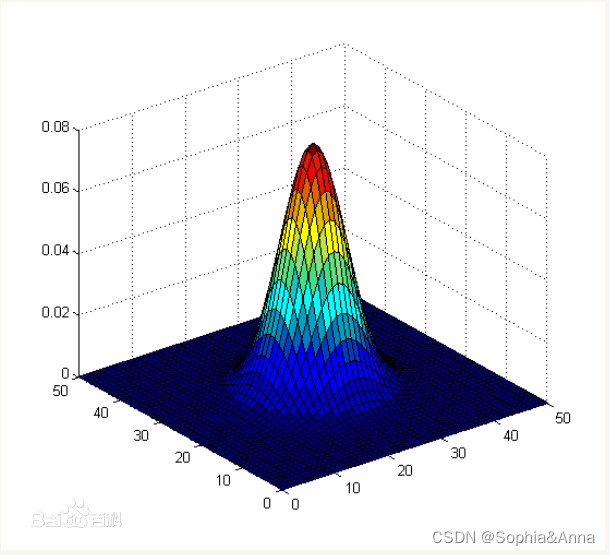
但是权重的大小设置非常麻烦,那么有没有一种方式能够自动生成呢? 这个就是需要用到高斯函数
高斯函数呈现出的特征就是中间高,两边低的钟形
高斯模糊通常被用来减少图像噪声以及降低细节层次。
代码实现
import cv2
import numpy as np
import matplotlib.pyplot as plt# 写代码时用的jupyter,cv2.imshow总是卡死,所以用的plt方便显示图像
def imgshow(img):img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)plt.imshow(img)plt.show()dog_img = cv2.imread('/Users/guojun/Desktop/444.png',cv2.IMREAD_COLOR)
# 高斯模糊 参数1:图像 参数2:卷积核大小, 参数3:标准差越大,去除高斯噪声能力越强,图像越模糊
dog_gaussianblur = cv2.GaussianBlur(dog_img,(15,15),50)
imgshow(dog_gaussianblur)中值滤波
对邻近的像素点进行灰度排序,然后取中间值,它能有效去除图像中的椒盐噪声
操作原理:
- 卷积域内的像素值从小到大排序
- 取中间值作为卷积输出
代码实现
import cv2
import numpy as np
import matplotlib.pyplot as plt# 写代码时用的jupyter,cv2.imshow总是卡死,所以用的plt方便显示图像
def imgshow(img):img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)plt.imshow(img)plt.show()img = cv2.imread('/Users/guojun/Desktop/444.png',cv2.IMREAD_COLOR)
# 中值滤波 参数1:图像 参数2:卷积核大小,卷积核必须为单数
dst = cv2.medianBlur(img,11)
imgshow(dst)Sobel算子
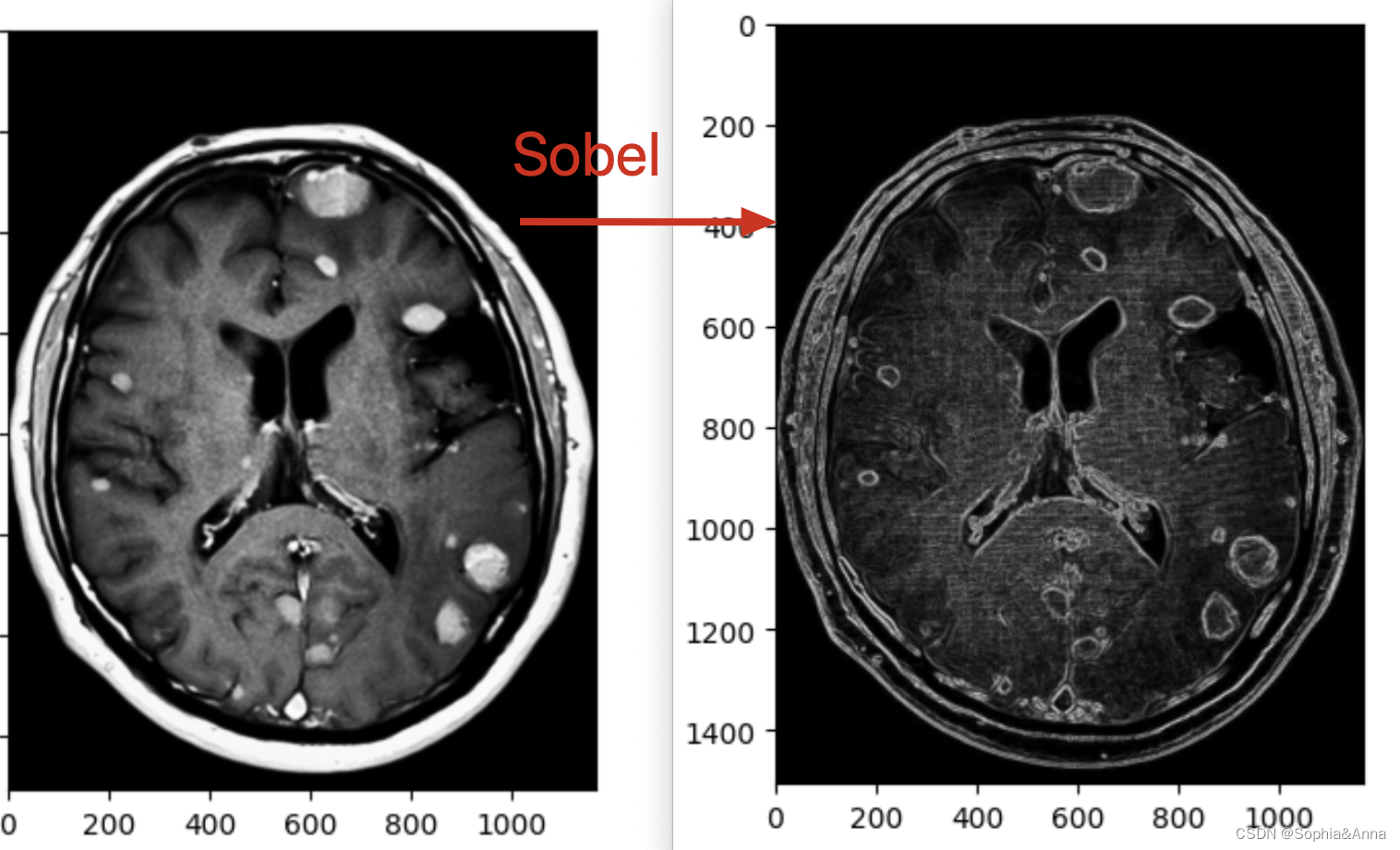
Sobel算子是像素图像边缘检测中最重要的算子之一,在机器学习、数字媒体、计算机视觉等信息科技领域起着举足轻重的作用。在技术上,它是一个离散的一阶差分算子,用来计算图像亮度函数的一阶梯度之近似值。在图像的任何一点使用此算子,将会产生该点对应的梯度矢量。
使用方式:
- 原图---> x 方向sobel
- 原图----> y 方向sobel
- xy合在一起
水平梯度:
垂直梯度:
合成:
备注:为了提高计算机效率我们通常会使用: G = |Gx|+|Gy|
代码实现
import cv2
import numpy as np
import matplotlib.pyplot as plt# 写代码时用的jupyter,cv2.imshow总是卡死,所以用的plt方便显示图像
def imgshow(img):img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)plt.imshow(img)plt.show()# Sobel算子
img = cv2.imread('/Users/guojun/Desktop/mri.jpg',cv2.IMREAD_GRAYSCALE)# Sobel算子:x方向求导
# 参数1:图像,参数2:图像的深度,-1表示和原图相同,参数3:x方向求导的阶数 参数4:y方向求导的阶数
x_sobel = cv2.Sobel(img,cv2.cv2.CV_32F,1,0)
# 将图像转为8位int
x_sobel = cv2.convertScaleAbs(x_sobel)
# imgshow(x_sobel)# Sobel算子:y方向求导
y_sobel = cv2.Sobel(img,cv2.cv2.CV_32F,0,1)
# 将图像转为8位int
y_sobel = cv2.convertScaleAbs(y_sobel)
# imgshow(y_sobel)# 将x,y方向的内容叠加起来
dst = x_sobel + y_sobel
imgshow(dst)Scharr算子
由于使用Sobel算子计算的时候有一些偏差, 所以opencv提供了sobel的升级版Scharr函数,计算比sobel更加精细.

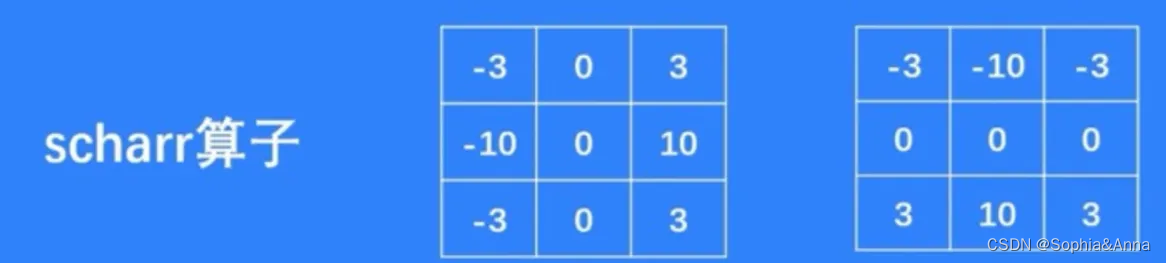
代码实现
import cv2
import numpy as np
import matplotlib.pyplot as plt# 写代码时用的jupyter,cv2.imshow总是卡死,所以用的plt方便显示图像
def imgshow(img):img = cv2.cvtColor(img,cv2.COLOR_BGR2RGB)plt.imshow(img)plt.show()# Scharr算子
img = cv2.imread('/Users/guojun/Desktop/mri.jpg',cv2.IMREAD_GRAYSCALE)# Scharr算子:x方向求导
# 参数1:图像,参数2:图像的深度,-1表示和原图相同,参数3:x方向求导的阶数 参数4:y方向求导的阶数
x_Scharr = cv2.Scharr(img,cv2.cv2.CV_32F,1,0)
# 将图像转为8位int
x_Scharr = cv2.convertScaleAbs(x_sobel)
# imgshow(x_sobel)# Scharr算子:y方向求导
y_Scharr = cv2.Sobel(img,cv2.cv2.CV_16S,0,1)
# 将图像转为8位int
y_Scharr = cv2.convertScaleAbs(y_sobel)
# imgshow(y_sobel)# 将x,y方向的内容叠加起来
dst = x_Scharr + y_Scharr
imgshow(dst)拉普拉斯算子
通过拉普拉斯变换后增强了图像中灰度突变处的对比度,使图像中小的细节部分得到增强,使图像的细节比原始图像更加清晰。
相关文章:

OpenCV轻松入门(八)——图片卷积
对图像和滤波矩阵进行逐个元素相乘再求和的操作就相当于将一个二维的函数移动到另一个二维函数的所有位置,这个操作就叫卷积。 卷积需要4个嵌套循环,所以它并不快,除非我们使用很小的卷积核。这里一般使用3x3或者5x5 图像滤波 图像滤波是尽…...

鸿蒙HarmonyOS开发规范-完善中
代码规范 所有文件,包括自动生成的编译文件package.json都要格式化(IDE快捷键CtrlAltL);函数命名,C大驼峰,TS、JS小驼峰,函数命名注意动宾结构;静态常量需使用全大写,文…...
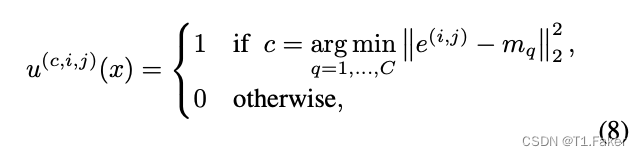
神经网络压缩图像
简介 典型的压缩管道由四个组件组成: 编码:输入图像 x x x通过编码器函数 ε \varepsilon ε,将其转换为潜在表示 z z z。 量化:截断 z z z以丢弃一些不重要的信息 熵编码:使用某种形式的熵编码(例如&…...
)
Catagory(rt)
继承(IMP融合):支持super命令码;继承推荐重写 分类(IMP替换):不支持super命令码;分类推荐组合 //替换(原来没了/破坏掉原来IMP/分类(替换特性)) 情况1: 自封装(组件化)开源库>分类推荐组合 情况2:逆向分析> 有意替换>分类IMP替换 #import "CatagoryViewContro…...
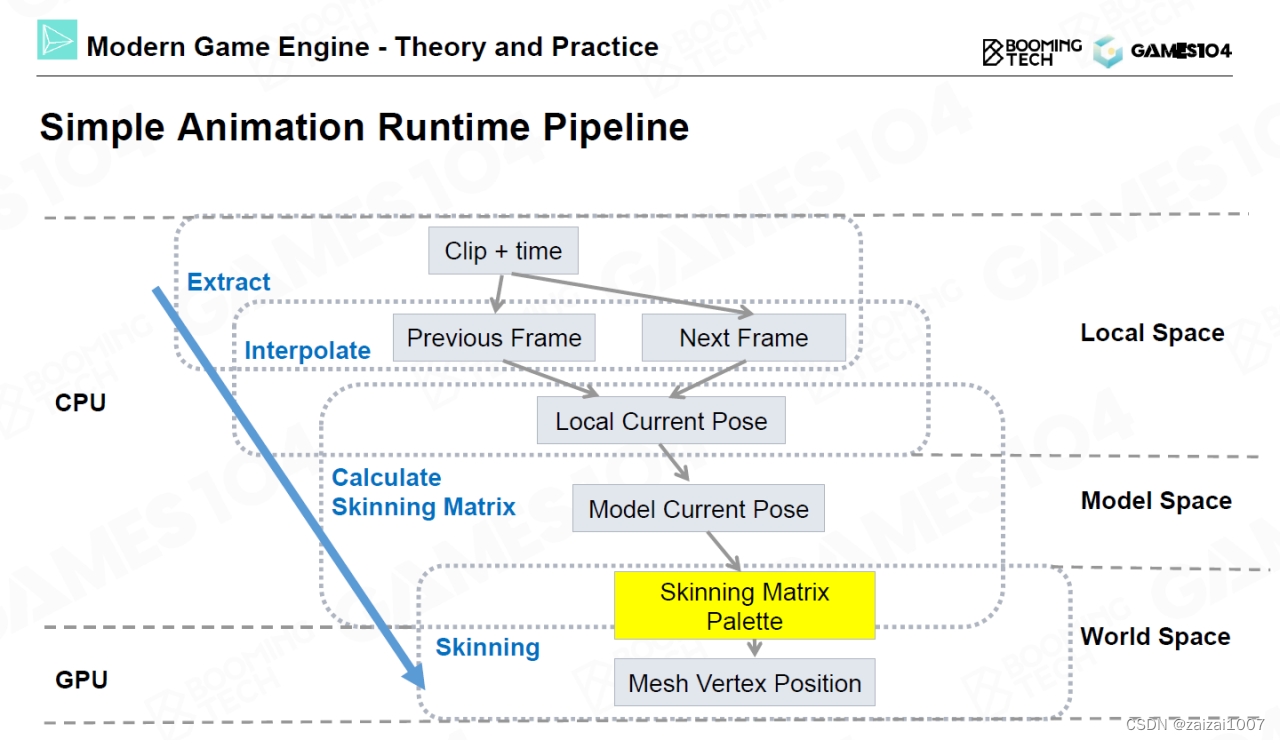
Games104 现代游戏引擎3
Sprite Animation 序列帧动画 自由度(degrees of freedom,DoF)对于刚体而言描述它的运动需要3个位移3个旋转,一共6个自由度 顶点动画(per-vertex animation)利用网格的顶点来控制运动。此时网格上的每个顶…...

【云计算】混合云分类
《混合云》系列,共包含以下 3 篇文章: 【云计算】混合云概述【云计算】混合云分类【云计算】混合云组成、应用场景、风险挑战 😊 如果您觉得这篇文章有用 ✔️ 的话,请给博主一个一键三连 🚀🚀Ὠ…...
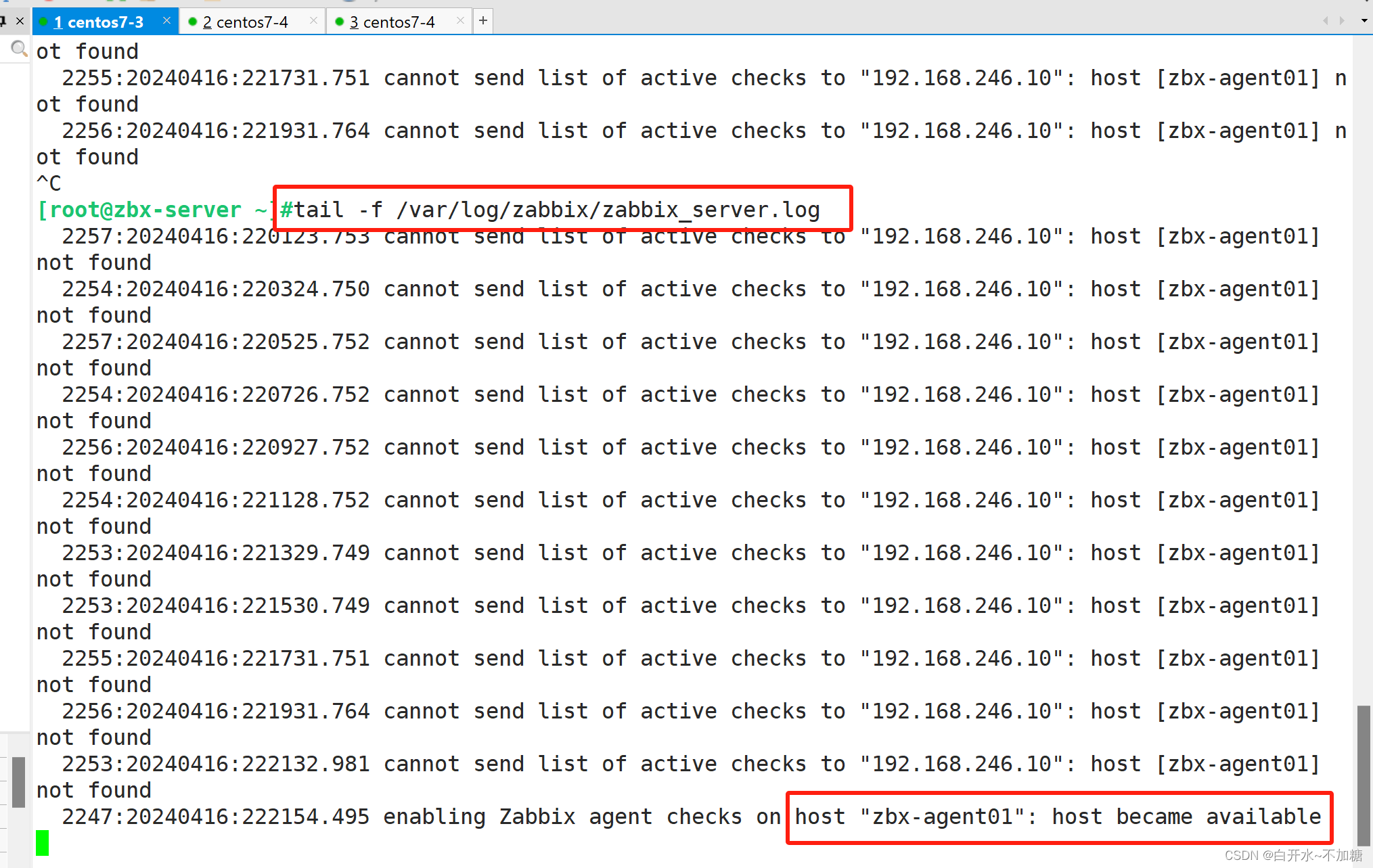
探索分布式系统监控zabbix------------自动发现与自动注册
目录 一、部署 zabbix 服务端 二、部署 zabbix 客户端 2.1环境准备 2.2服务端和客户端都配置时间同步 (ntp) 2.2.1服务端zbx-server 2.2.2服务端zabbix-agent01客户端 2.3客户端配置时区,与服务器保持一致 2.4设置 zabbix 的下载源&…...
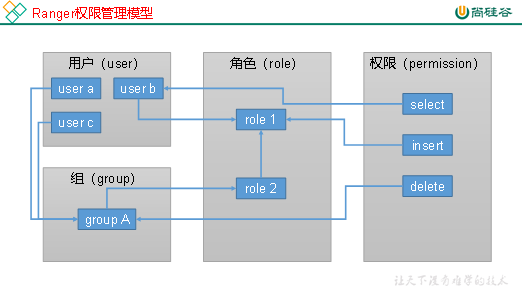
权限管理Ranger详解
文章目录 一、Ranger概述与安装1、Ranger概述1.1 Ranger介绍1.2 Ranger的目标1.3 Ranger支持的框架1.4 Ranger的架构1.5 Ranger的工作原理 2、Ranger安装2.1 创建系统用户和Kerberos主体2.2 数据库环境准备2.3 安装RangerAdmin2.4 启动RangerAdmin 二、Ranger简单使用1、安装 R…...
WPF Extended.Wpf.Toolkit 加载界面
1、NuGet 中安装 Extended.Wpf.Toolkit 。 2、在MainWindow.xaml中添加xmlns:tk"http://schemas.xceed.com/wpf/xaml/toolkit" 。 MainWindow.xaml 代码如下。 <Window x:Class"WPF_Extended_Wpf_Toolkit_Loading.MainWindow" xmlns"ht…...
【切换网络连接后】VMware虚拟机网络配置【局域网通信】
初次安装Linux虚拟机以及切换网络都需要配置虚拟机网络, 从而使得win主机内通过远程连接工具能够连接该虚拟机, 而不是在虚拟机内操作。 本片文章你将了解到网络切换后如何配置虚拟机网络的一些基础操作,以及局域网通信的一些基础知识。 …...

革新鞋服零售:数据驱动的智能商品管理 解锁库存优化与高效增长
国内鞋服零售企业经过多年的发展,已经形成诸多家喻户晓的品牌,但近年来一些企业的库存问题也时常显现,高库存不仅困扰着品牌商,也使一些多年合作良好的经销商深受其害,当下的订货会制度在初期帮助企业解决了盲目生产的…...
word文件的创建时间和修改时间可以更改吗?答案是肯定的 文件属性修改的方法
一,引言 在日常生活和工作中,我们经常需要处理各种Word文件。有时,由于某些原因,我们可能需要更改Word文件的创建时间和修改时间。虽然这听起来可能有些复杂,但实际上,通过一些简单的方法和工具࿰…...

redisson -- 延迟队列RDelayedQueue
1.maven配置 <!-- 用于管理起步工程的依赖管理 --><parent><groupId>org.springframework.boot</groupId><artifactId>spring-boot-starter-parent</artifactId><version>2.6.11</version><relativePath/> </parent…...

Flex弹性盒子布局案例(认识弹性布局)
一、导航菜单 此示例创建了一个水平导航菜单,其中链接在 Flex 容器中等距分布。 HTML结构: <nav class"nav-menu"><a href"#">Home</a><a href"#">About</a><a href"#">…...

【ros2】ros1和ros2可以同时在一台机器上运行吗
可以,ROS 1 和 ROS 2 是两个不同版本的 Robot Operating System (ROS),它们分别有着各自的架构、消息传递机制以及配套工具集。尽管存在这些差异,ROS 1 和 ROS 2 可以在同一台 Ubuntu 系统上共存并独立运行。以下是一些关键点来说明如何实现这…...

PMSM MATLAB
// s-function搭建变参数PMSM模型 ///...
笔记本电脑上的聊天机器人: 在英特尔 Meteor Lake 上运行 Phi-2
对应于其强大的能力,大语言模型 (LLM) 需要强大的算力支撑,而个人计算机上很难满足这一需求。因此,我们别无选择,只能将它们部署至由本地或云端托管的性能强大的定制 AI 服务器上。 为何需要将 LLM 推理本地化 如果我们可以在典配…...
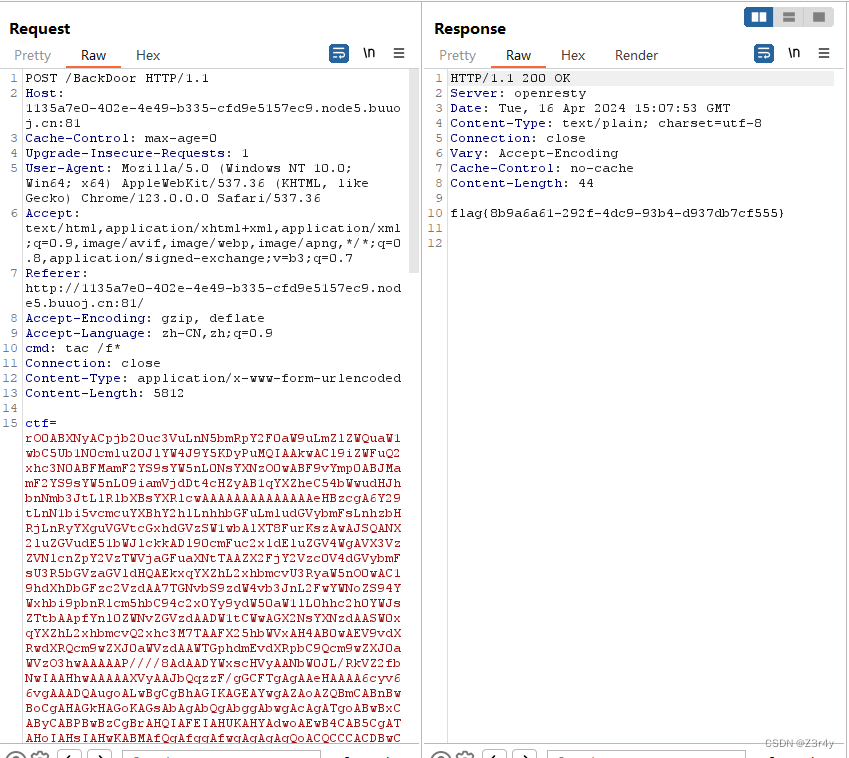
【Web】陇原战“疫“2021网络安全大赛 题解
目录 CheckIN eaaasyphp EasyJaba CheckIN 拿到附件,贴出关键代码 func getController(c *gin.Context) {cmd : exec.Command("/bin/wget", c.QueryArray("argv")[1:]...)err : cmd.Run()if err ! nil {fmt.Println("error: ", …...
010Node.js自定义模块通过exports的使用,两种暴露的方法及区别(二)
module/request.js var obj{get:function(){console.log(从服务器获取数据);},post:function(){console.log(提交数据);} }exports.xxxxobj;//方法一 { xxxx: { get: [Function: get], post: [Function: post] } }//module.exportsobj;//方法二 //{ get: [Function: g…...
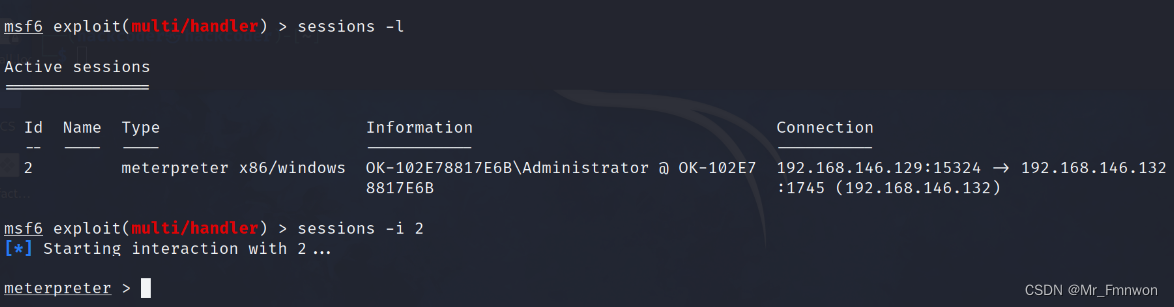
【CVE-2010-2883】进行钓鱼攻击的研究
最近作业中研究APT攻击,了解到2011年前后披露的LURID-APT,其中敌手利用了各种版本的文件查看器的漏洞实现攻击。CVE-2010-2883就是其中被利用的一个adobe reader的漏洞。特此复现,更好的研究和防范APT攻击。 本文仅仅是对相关漏洞利用的学习…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

ardupilot 开发环境eclipse 中import 缺少C++
目录 文章目录 目录摘要1.修复过程摘要 本节主要解决ardupilot 开发环境eclipse 中import 缺少C++,无法导入ardupilot代码,会引起查看不方便的问题。如下图所示 1.修复过程 0.安装ubuntu 软件中自带的eclipse 1.打开eclipse—Help—install new software 2.在 Work with中…...

【Go语言基础【12】】指针:声明、取地址、解引用
文章目录 零、概述:指针 vs. 引用(类比其他语言)一、指针基础概念二、指针声明与初始化三、指针操作符1. &:取地址(拿到内存地址)2. *:解引用(拿到值) 四、空指针&am…...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...

android RelativeLayout布局
<?xml version"1.0" encoding"utf-8"?> <RelativeLayout xmlns:android"http://schemas.android.com/apk/res/android"android:layout_width"match_parent"android:layout_height"match_parent"android:gravity&…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...
