课题学习(二十一)----姿态更新的四元数算法推导
声明:本人水平有限,博客可能存在部分错误的地方,请广大读者谅解并向本人反馈错误。
最近需要使用AEKF对姿态进行结算,所以又对四元数进了深入的学习,本篇博客仅对四元数进行推导,后续会对基于四元数的AEKF算法进行实现。
一、 坐标变化
1.1 基本概念
首先,我对参考坐标系进行了定义,即选择“东-北-天”(或者叫做“右-前-上”),如下图:

并且记:
- p(pitch):俯仰角(绕X轴旋转);
- r(roll):横滚角(绕Y轴旋转);
- y(yaw):航向角(绕Z轴旋转);
并且设角度逆时针旋转为正。
1.2 绕X轴旋转

由上图可以得出由X-Y-Z–>X’-Y’-Z’的变换矩阵:
[ 1 0 0 0 c o s p s i n p 0 − s i n p c o s p ] \begin{bmatrix} 1&0&0 \\ 0&cosp&sinp\\0&-sinp&cosp \end{bmatrix} 1000cosp−sinp0sinpcosp
1.3 绕Y轴旋转

变换矩阵:
[ c o s r 0 − s i n r 0 1 0 s i n r 0 c o s r ] \begin{bmatrix} cosr&0&-sinr \\ 0&1&0\\sinr&0&cosr \end{bmatrix} cosr0sinr010−sinr0cosr
1.4 绕Z轴旋转

变换矩阵:
[ c o s y s i n y 0 − s i n y c o s y 0 0 0 1 ] \begin{bmatrix} cosy&siny&0\\ -siny&cosy&0\\0&0&1 \end{bmatrix} cosy−siny0sinycosy0001
1.5 坐标变换矩阵
在此假设旋转的顺序为:Z–>X–>Y,那么最后的坐标变换矩阵为(注意:一定要把矩阵相乘的顺序搞对):
C n b = C 2 b ( 绕 Y 轴旋转矩阵 ) ∗ C 1 2 ( 绕 X 轴旋转矩阵 ) ∗ C n 1 ( 绕 Z 轴旋转矩阵 ) C_n^b=C_2^b(绕Y轴旋转矩阵)*C_1^2(绕X轴旋转矩阵)*C_n^1(绕Z轴旋转矩阵) Cnb=C2b(绕Y轴旋转矩阵)∗C12(绕X轴旋转矩阵)∗Cn1(绕Z轴旋转矩阵)
= [ c o s r 0 − s i n r 0 1 0 s i n r 0 c o s r ] ∗ [ 1 0 0 0 c o s p s i n p 0 − s i n p c o s p ] ∗ [ c o s y s i n y 0 − s i n y c o s y 0 0 0 1 ] =\begin{bmatrix} cosr&0&-sinr \\ 0&1&0\\sinr&0&cosr \end{bmatrix}*\begin{bmatrix} 1&0&0 \\ 0&cosp&sinp\\0&-sinp&cosp \end{bmatrix}*\begin{bmatrix} cosy&siny&0\\ -siny&cosy&0\\0&0&1 \end{bmatrix} = cosr0sinr010−sinr0cosr ∗ 1000cosp−sinp0sinpcosp ∗ cosy−siny0sinycosy0001
= [ c o s r ∗ c o s y − s i n p ∗ s i n r ∗ s i n y c o s y ∗ s i n y + s i n p ∗ s i n r ∗ c o s y − c o s p ∗ s i n r − c o s p ∗ s i n y c o s p ∗ c o s y s i n p s i n r ∗ c o s y + s i n p ∗ c o s r ∗ s i n y s i n y ∗ s i n r − s i n p ∗ c o s r ∗ c o s y c o s r c o s p ] =\begin{bmatrix} cosr*cosy-sinp*sinr*siny&cosy*siny+sinp*sinr*cosy&-cosp*sinr \\ -cosp*siny&cosp*cosy&sinp\\ sinr*cosy+sinp*cosr*siny&siny*sinr-sinp*cosr*cosy&cosrcosp \end{bmatrix} = cosr∗cosy−sinp∗sinr∗siny−cosp∗sinysinr∗cosy+sinp∗cosr∗sinycosy∗siny+sinp∗sinr∗cosycosp∗cosysiny∗sinr−sinp∗cosr∗cosy−cosp∗sinrsinpcosrcosp
注意: C n b C_n^b Cnb是n系到b系的坐标变换矩阵,而在求解时,是将b系的姿态变换到n系上求解,所以最后要对 C n b C_n^b Cnb转置变为 C b n C_b^n Cbn 。
C b n = ( C n b ) T C_b^n = (C_n^b)^T Cbn=(Cnb)T
= [ c o s r ∗ c o s y − s i n p ∗ s i n r ∗ s i n y − c o s p ∗ s i n y s i n r ∗ c o s y + s i n p ∗ c o s r ∗ s i n y c o s y ∗ s i n y + s i n p ∗ s i n r ∗ c o s y c o s p ∗ c o s y s i n y ∗ s i n r − s i n p ∗ c o s r ∗ c o s y − c o s p ∗ s i n r s i n p c o s r ∗ c o s p ] =\begin{bmatrix} cosr*cosy-sinp*sinr*siny&-cosp*siny&sinr*cosy+sinp*cosr*siny \\ cosy*siny+sinp*sinr*cosy&cosp*cosy&siny*sinr-sinp*cosr*cosy\\ -cosp*sinr&sinp&cosr*cosp \end{bmatrix} = cosr∗cosy−sinp∗sinr∗sinycosy∗siny+sinp∗sinr∗cosy−cosp∗sinr−cosp∗sinycosp∗cosysinpsinr∗cosy+sinp∗cosr∗sinysiny∗sinr−sinp∗cosr∗cosycosr∗cosp
= [ T 11 T 12 T 13 T 21 T 22 T 23 T 31 T 32 T 33 ] =\begin{bmatrix} T_{11}&T_{12}&T_{13}\\ T_{21}&T_{22}&T_{23}\\ T_{31}&T_{32}&T_{33} \end{bmatrix} = T11T21T31T12T22T32T13T23T33
二、 四元数
2.1 基础概念回忆
在课题学习(十七)----姿态更新的四元数算法总结博客中,已经对四元数进行了比较详细的讲解,在这里只对四元数的物理意义重述一次:

其中, u → R = [ l , m , n ] \overrightarrow{u}^R=[l,m,n] uR=[l,m,n],且四元数定义为:
{ q 0 = c o s θ 2 q 1 = l s i n θ 2 q 2 = m s i n θ 2 q 3 = n s i n θ 2 \begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases} ⎩ ⎨ ⎧q0=cos2θq1=lsin2θq2=msin2θq3=nsin2θ
2.2 绕X轴旋转

把 u → R = [ l , m , n ] = [ 1 , 0 , 0 ] \overrightarrow{u}^R=[l,m,n]=[1,0,0] uR=[l,m,n]=[1,0,0]代入 { q 0 = c o s θ 2 q 1 = l s i n θ 2 q 2 = m s i n θ 2 q 3 = n s i n θ 2 \begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases} ⎩ ⎨ ⎧q0=cos2θq1=lsin2θq2=msin2θq3=nsin2θ,那么就可以得到绕X轴的四元数 q x = [ c o s p 2 , s i n p 2 , 0 , 0 ] q_x=[cos\frac{p}{2},sin\frac{p}{2},0,0] qx=[cos2p,sin2p,0,0]
2.3 绕Y、Z轴旋转

绕Y轴旋转:把 u → R = [ l , m , n ] = [ 0 , 1 , 0 ] \overrightarrow{u}^R=[l,m,n]=[0,1,0] uR=[l,m,n]=[0,1,0]代入 { q 0 = c o s θ 2 q 1 = l s i n θ 2 q 2 = m s i n θ 2 q 3 = n s i n θ 2 \begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases} ⎩ ⎨ ⎧q0=cos2θq1=lsin2θq2=msin2θq3=nsin2θ,那么就可以得到绕Y轴的四元数 q y = [ c o s r 2 , 0 , s i n r 2 , 0 ] q_y=[cos\frac{r}{2},0,sin\frac{r}{2},0] qy=[cos2r,0,sin2r,0]
绕Y轴旋转:把 u → R = [ l , m , n ] = [ 0 , 0 , 1 ] \overrightarrow{u}^R=[l,m,n]=[0,0,1] uR=[l,m,n]=[0,0,1]代入 { q 0 = c o s θ 2 q 1 = l s i n θ 2 q 2 = m s i n θ 2 q 3 = n s i n θ 2 \begin{cases}q_0=cos\frac{\theta}{2}\\q_1=lsin\frac{\theta}{2}\\q_2=msin\frac{\theta}{2}\\q_3=nsin\frac{\theta}{2}\end{cases} ⎩ ⎨ ⎧q0=cos2θq1=lsin2θq2=msin2θq3=nsin2θ,那么就可以得到绕Z轴的四元数 q z = [ c o s y 2 , 0 , 0 , s i n y 2 ] q_z=[cos\frac{y}{2},0,0,sin\frac{y}{2}] qz=[cos2y,0,0,sin2y]
2.4 用四元数表示旋转矩阵(坐标变换矩阵)
在第一节中,我们规定了旋转顺序为:Z–>X–>Y,那么最后四元数的旋转矩阵为(参考博客:《欧拉角和四元数之间转换公式推导》): q = q z ⨂ q x ⨂ q y q = q_z \bigotimes q_x\bigotimes q_y q=qz⨂qx⨂qy
" ⨂ \bigotimes ⨂"运算在《课题学习(十七)----姿态更新的四元数算法总结 》博客中也有介绍,大家可以参考:

在这部分,我有一点未搞清楚,就是四元数的乘法不满足交换律,即“ P ⨂ Q ≠ Q ⨂ P \bold P \bigotimes \bold Q \neq \bold Q \bigotimes \bold P P⨂Q=Q⨂P” ,那么公式 q = q z ⨂ q x ⨂ q y q = q_z \bigotimes q_x\bigotimes q_y q=qz⨂qx⨂qy不能更换相乘的顺序,所以…我搞不懂这个顺序是否正确。
反正最后按照 q = q z ⨂ q x ⨂ q y q = q_z \bigotimes q_x\bigotimes q_y q=qz⨂qx⨂qy得到的四元数为:

三、四元数与坐标变换矩阵的关系
在秦永元老师的《惯性导航(第二版)》9.2.2节(P248-P253)中对四元数与坐标变换矩阵的关系进行了推导,大家可以参考学习。
最后得到的四元数表示的坐标变换矩阵为:
C b n = [ q 0 2 + q 1 2 − q 2 2 − q 3 2 2 ( q 1 q 2 − q 3 q 0 ) 2 ( q 1 q 3 + q 2 q 0 ) 2 ( q 1 q 2 + q 3 q 0 ) q 0 2 − q 1 2 + q 2 2 − q 3 2 2 ( q 2 q 3 − q 1 q 0 ) 2 ( q 1 q 3 − q 2 q 0 ) 2 ( q 2 q 3 + q 1 q 0 ) q 0 2 − q 1 2 − q 2 2 + q 3 2 ] C_b^n=\begin{bmatrix} q^2_{0}+q^2_{1}-q^2_{2}-q^2_{3} &2(q_{1}q_{2}-q_{3}q_{0})&2(q_{1}q_{3}+q_{2}q_{0})\\ 2(q_{1}q_{2}+q_{3}q_{0}) &q^2_{0}-q^2_{1}+q^2_{2}-q^2_{3}&2(q_{2}q_{3}-q_{1}q_{0})\\ 2(q_{1}q_{3}-q_{2}q_{0})&2(q_{2}q_{3}+q_{1}q_{0})&q^2_{0}-q^2_{1}-q^2_{2}+q^2_{3} \end{bmatrix} Cbn= q02+q12−q22−q322(q1q2+q3q0)2(q1q3−q2q0)2(q1q2−q3q0)q02−q12+q22−q322(q2q3+q1q0)2(q1q3+q2q0)2(q2q3−q1q0)q02−q12−q22+q32
同时,大家可以对本博客2.4节推导出来的四元数进行反推,比如我计算了 2 ( q 2 q 3 + q 1 q 0 ) 2(q_{2}q_{3}+q_{1}q_{0}) 2(q2q3+q1q0),最后得到的结果就是 s i n p sinp sinp:

四、往期回顾
课题学习(一)----静态测量
课题学习(二)----倾角和方位角的动态测量方法(基于磁场的测量系统)
课题学习(三)----倾角和方位角的动态测量方法(基于陀螺仪的测量系统)
课题学习(四)----四元数解法
课题学习(五)----阅读论文《抗差自适应滤波的导向钻具动态姿态测量方法》
课题学习(六)----安装误差校准、实验方法
课题学习(七)----粘滑运动的动态算法
课题学习(八)----卡尔曼滤波动态求解倾角、方位角
课题学习(九)----阅读《导向钻井工具姿态动态测量的自适应滤波方法》论文笔记
课题学习(十)----阅读《基于数据融合的近钻头井眼轨迹参数动态测量方法》论文笔记
课题学习(十一)----阅读《Attitude Determination with Magnetometers and Accelerometers to Use in Satellite》
课题学习(十二)----阅读《Extension of a Two-Step Calibration Methodology to Include Nonorthogonal Sensor Axes》
课题学习(十三)----阅读《Calibration of Strapdown Magnetometers in Magnetic Field Domain》论文笔记
课题学习(十四)----三轴加速度计+三轴陀螺仪传感器-ICM20602
课题学习(十五)----阅读《测斜仪旋转姿态测量信号处理方法》论文
课题学习(十六)----阅读《Continuous Wellbore Surveying While Drilling Utilizing MEMS Gyroscopes Based…》论文
课题学习(十七)----姿态更新的四元数算法总结
课题学习(十八)----捷联测试电路设计与代码实现(基于MPU6050和QMC5883L)
课题学习(十九)----Allan方差:陀螺仪噪声分析
课题学习(二十)----阅读《近钻头井斜动态测量重力加速度信号提取方法研究》论文
相关文章:

课题学习(二十一)----姿态更新的四元数算法推导
声明:本人水平有限,博客可能存在部分错误的地方,请广大读者谅解并向本人反馈错误。 最近需要使用AEKF对姿态进行结算,所以又对四元数进了深入的学习,本篇博客仅对四元数进行推导,后续会对基于四元数的…...

NL2SQL进阶系列(5):论文解读业界前沿方案(DIN-SQL、C3-SQL、DAIL-SQL、SQL-PaLM)、新一代数据集BIRD-SQL解读
NL2SQL进阶系列(5):论文解读业界前沿方案(DIN-SQL、C3-SQL、DAIL-SQL)、新一代数据集BIRD-SQL解读 NL2SQL基础系列(1):业界顶尖排行榜、权威测评数据集及LLM大模型(Spider vs BIRD)全面对比优劣分析[Text2…...

双指针运用:删除重复元素、移除元素
26.删除重复元素 题目描述 给你一个 非严格递增排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元…...

什么是三高架构
三高架构是指在软件系统设计与开发中,注重解决高并发性、高可用性和高性能的架构设计模式。 高并发性:指系统能够处理大量并发请求的能力。在高并发场景下,系统需要具备有效的并发处理机制,以保证系统能够快速、准确地响应大量并…...

Unity 对APK签名
关键代码 PS D:\UnityProject\YueJie> jarsigner -verbose -keystore D:\UnityProject\YueJie\user.keystore -signedjar D:\UnityProject\YueJie\meizuemptyapk-release-signed.apk D:\UnityProject\YueJie\MeizuEmpty-release-unsigned.apk 1 示例 # jarsigner的命令格…...

合成孔径雷达干涉测量InSAR数据处理、地形三维重建、形变信息提取、监测等应用
合成孔径雷达干涉测量(Interferometric Synthetic Aperture Radar, InSAR)技术作为一种新兴的主动式微波遥感技术,凭借其可以穿过大气层,全天时、全天候获取监测目标的形变信息等特性,已在地表形变监测、DEM生成、滑坡…...
)
QT进阶------------------QPushButton(快速添加按钮与使用)
1、解决如何快速的添加按钮 在qt中,通常我们喜欢一个按钮添加一个信号与槽,但是这样写太过浪费时间。要是多个按钮那不是要写30个信号与槽,说实话,我不太喜欢这样。 在ui中,只要拖动按钮,会自动生成按钮的名…...
Vue项目管理器创建项目
黑马程序员JavaWeb开发教程 文章目录 1、创建新项目2、详情3、预设4、功能5、配置6、是否保存为预设模板7、正在创建项目8、创建完成 1、创建新项目 2、详情 3、预设 选择手动,点击下一步 4、功能 只需要额外选择一项–Router 即可,其余的保持默认&a…...
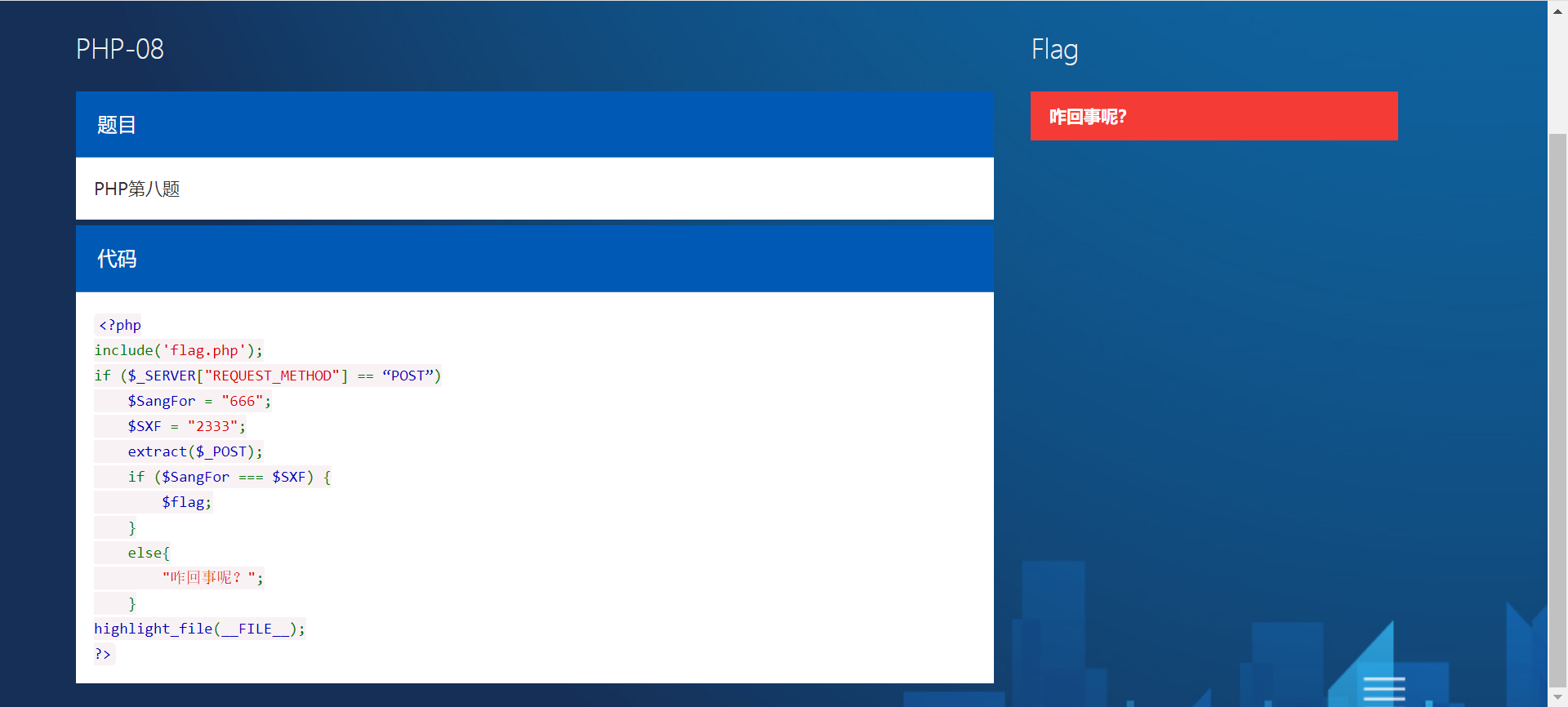
PHP-extract变量覆盖
[题目信息]: 题目名称题目难度PHP-extract变量覆盖1 [题目考点]: 变量覆盖指的是用我们自定义的参数值替换程序原有的变量值,一般变量覆盖漏洞需要结合程序的其它功能来实现完整的攻击。 经常导致变量覆盖漏洞场景有:$$&#x…...

研究表明,全球互联网流量竟有一半来自机器人
据Cyber News消息,Thales Imperva Bad Bot近期做了一份报告,显示在2023年有49.6%的互联网流量竟来自机器人,比上一年增长 2%,达到自2013年以来观察到的最高水平。 报告称,这一趋势正对企业组织产生负面影响,…...

橡胶衬板的更换与安装
橡胶衬板的更换与安装 橡胶衬板作为一种重要的工业材料,广泛应用于各种设备和机器中,以提供减震、防滑、耐磨等功能。然而,随着时间的推移和使用频率的增加,橡胶衬板可能会磨损或老化,需要及时更换和安装。本文将介绍…...

Compose 简单组件
文章目录 Compose 简单组件TextText属性使用AnnotatedStringSpanStyleParagraphStyle SelectionContainer 和 DisableSelectionClickableText TextFieldTextField属性使用OutlinedTextFieldBasicTextFieldKeyboardOptions 键盘属性KeyboardActions IME动作 ButtonButton属性使用…...

第十一届蓝桥杯省赛真题(C/C++大学B组)
目录 试题A :门牌制作 试题B :既约分数 试题C :蛇形填数 试题D :跑步训练 试题E :七段码 试题F :成绩统计 试题G :回文日期 试题H :字串分值 试题I :平面切分&a…...
Qt 实战(2)搭建开发环境 | 2.1、Windows下安装QT
一、Windows下安装QT 1、QT官网 QT官网:https://download.qt.io/,打开官网地址,如下: 目录结构介绍 目录说明snapshots预览版,最新的开发测试中的 Qt 库和开发工具onlineQt 在线安装源official_releases正式发布版&am…...
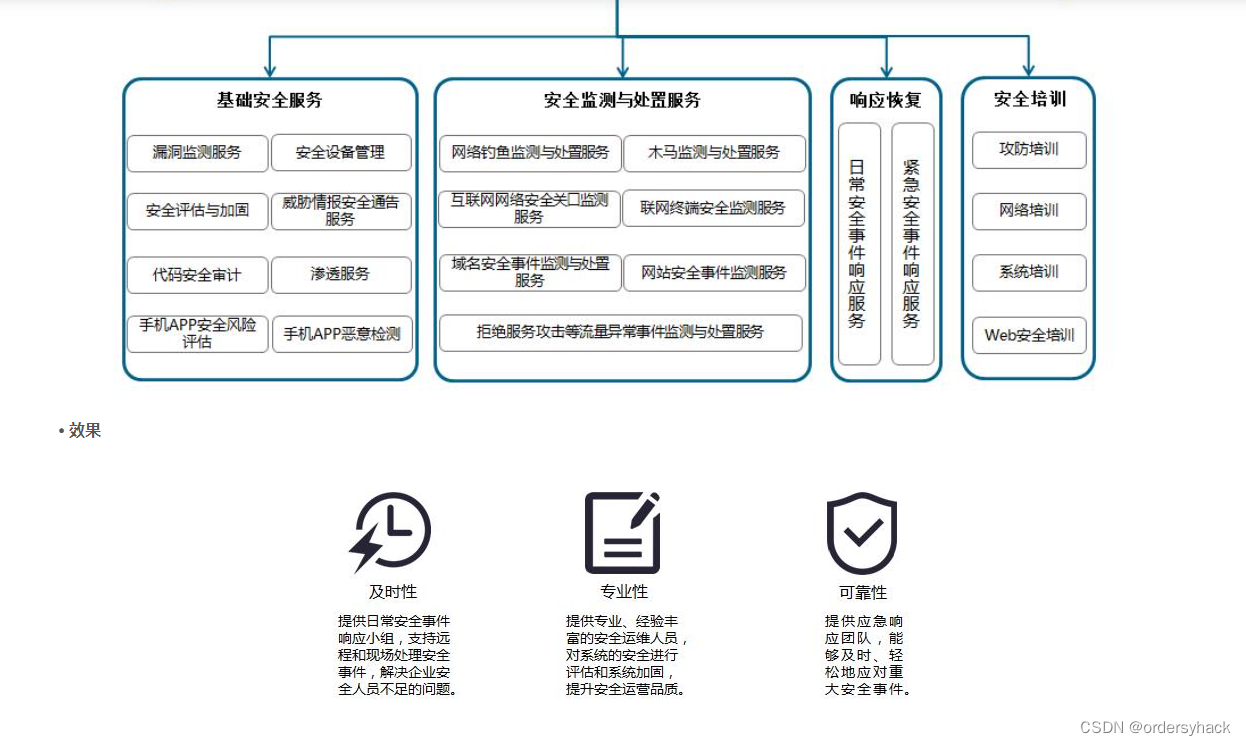
校园通用型发生网络安全事件解决方案
已知校园多教学楼、多教学机房、非标网络机房缺乏防护设备、检测设备、安全保护软件(杀软) 切断所有外网,断网理!!!!!!!!!!!…...

数通HCIE考试分享:考前心态很重要,心情放松好过一次练习
誉天数通HCIE晚班火热预约中!真机实验考前辅导备考资料,名师保驾护航,助你稳定通关!识别二维码,即可获取免费试听名额! 备考阶段 我是去年10月底完成了笔试考试,在笔试之前就将PY的课程过了一遍…...
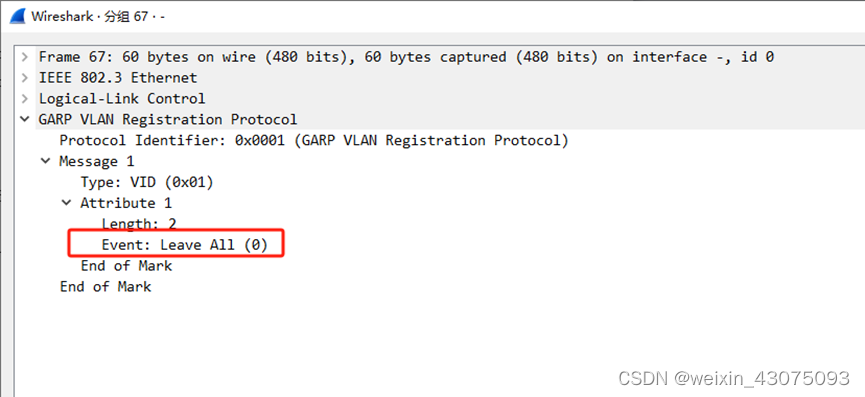
GVRP协议与动态、静态vlan
一、GVRP协议使用场景 1、当实际组网复杂到网络管理员无法短时间内了解网络的拓扑结构,或者是整个网络的VLAN太多时,工作量会非常大,而且非常容易配置错误。在这种情况下,用户可以通过GVRP的VLAN自动注册功能完成VLAN的配置。 2、…...

shell脚本启动jar包
1、启动脚本的命令start.sh # 设置jar包名称 JAR_NAME"ruoyi-admin.jar" # 使用pgrep查找jar包名称的进程,如果存在,返回0(表示找到了进程) if pgrep -f "$JAR_NAME" >/dev/null thenecho "Jar进程已…...

qt 元对象系统及属性系统
Qt元对象系统(QMetaObject) Qt 的元对象系统叫 Meta-Object-System,提供了对象之间通信的信号与槽机制、运行时类型信息和动态属性系统。即使编译器不支持RTTI(RTTI的实现耗费了很大的时间和存储空间,这就会降低程序的性能)&…...

2024年MathorCup数学建模A题移动通信网络中PCI规划问题解题文档与程序
2024年第十四届MathorCup高校数学建模挑战赛 A题 移动通信网络中PCI规划问题 原题再现: 物理小区识别码(PCI)规划是移动通信网络中下行链路层上,对各覆盖小区编号进行合理配置,以避免 PCI 冲突、PCI 混淆以及 PCI 模3 千扰等现象。PCI 规划…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

跨链模式:多链互操作架构与性能扩展方案
跨链模式:多链互操作架构与性能扩展方案 ——构建下一代区块链互联网的技术基石 一、跨链架构的核心范式演进 1. 分层协议栈:模块化解耦设计 现代跨链系统采用分层协议栈实现灵活扩展(H2Cross架构): 适配层…...

Robots.txt 文件
什么是robots.txt? robots.txt 是一个位于网站根目录下的文本文件(如:https://example.com/robots.txt),它用于指导网络爬虫(如搜索引擎的蜘蛛程序)如何抓取该网站的内容。这个文件遵循 Robots…...

04-初识css
一、css样式引入 1.1.内部样式 <div style"width: 100px;"></div>1.2.外部样式 1.2.1.外部样式1 <style>.aa {width: 100px;} </style> <div class"aa"></div>1.2.2.外部样式2 <!-- rel内表面引入的是style样…...

代理篇12|深入理解 Vite中的Proxy接口代理配置
在前端开发中,常常会遇到 跨域请求接口 的情况。为了解决这个问题,Vite 和 Webpack 都提供了 proxy 代理功能,用于将本地开发请求转发到后端服务器。 什么是代理(proxy)? 代理是在开发过程中,前端项目通过开发服务器,将指定的请求“转发”到真实的后端服务器,从而绕…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

前端调试HTTP状态码
1xx(信息类状态码) 这类状态码表示临时响应,需要客户端继续处理请求。 100 Continue 服务器已收到请求的初始部分,客户端应继续发送剩余部分。 2xx(成功类状态码) 表示请求已成功被服务器接收、理解并处…...
