2021牛客OI赛前集训营-提高组(第四场) T3快速访问
2021牛客OI赛前集训营-提高组(第四场)
题目大意
有一棵n+1n+1n+1个节点的树,根节点为0。给你一个kkk,定义集合Si={j∈Z∣max(1,i−k)≤j<i}∪{0}S_i=\{j\in Z|\max(1,i-k)\leq j<i\}\cup\{0\}Si={j∈Z∣max(1,i−k)≤j<i}∪{0}。
Ai=∑j∈Sidis(i,j)2A_i=\sum\limits_{j\in S_i}dis(i,j)^2Ai=j∈Si∑dis(i,j)2,dis(i,j)dis(i,j)dis(i,j)指iii到jjj在树上的距离。求A1,A2,…,AnA_1,A_2,\dots,A_nA1,A2,…,An分别是多少。
题解
令aia_iai表示iii在树上的深度,注意根节点的深度为1。
那么dis(i,j)2=(ai+aj−2alca)2=ai2+aj2+2aiaj−4alcaai−4alcaaj+4alca2dis(i,j)^2=(a_i+a_j-2a_{lca})^2=a_i^2+a_j^2+2a_ia_j-4a_{lca}a_i-4a_{lca}a_j+4a_{lca}^2dis(i,j)2=(ai+aj−2alca)2=ai2+aj2+2aiaj−4alcaai−4alcaaj+4alca2
我们可以枚举iii,用树链剖分来维护jjj的值。
对于ai2a_i^2ai2,可以直接得出。
对于aj2a_j^2aj2,将所有在SiS_iSi中的jjj求前缀和即可。
对于2aiaj2a_ia_j2aiaj,对aja_jaj求前缀和,再乘上2ai2a_i2ai。
对于4alcaai4a_{lca}a_i4alcaai,对每个SiS_iSi中的jjj,都将jjj到根节点的路径上的点加1,然后查询iii到根节点的路径上的对应值的和,再乘上4ai4a_i4ai即可。
对于4alcaaj4a_{lca}a_j4alcaaj,对每个SiS_iSi中的jjj,都将jjj到根节点的路径上的点加aja_jaj,然后查询iii到根节点的路径上的对应值的和,再乘上444即可。
对于4alca24a_{lca}^24alca2,对每个SiS_iSi中的jjj,都将jjj到根节点的路径上的点加ak∗2−1a_k*2-1ak∗2−1(kkk表示当前节点),然后查询iii到根节点的路径上的对应值的和,因为x2=1+3+5+⋯+(x∗2−1)x^2=1+3+5+\cdots+(x*2-1)x2=1+3+5+⋯+(x∗2−1),所以这样求出的就是alca2a_{lca}^2alca2,然后乘444即可。
对于jjj进入集合或离开集合,在jjj到根节点的路径上进行区间修改即可。
为什么根节点的深度为1而不为0呢?因为只有根节点的深度为1,那么每个点到根节点的路径的长度才能等于这个点的深度,这样才能更好地实现。
时间复杂度为O(nlog2n)O(n\log^2 n)O(nlog2n)。
code
#include<bits/stdc++.h>
#define lc k<<1
#define rc k<<1|1
using namespace std;
int n,k,x,y,tot=0,d[500005],l[500005],r[500005],dep[500005],fa[500005],siz[500005],son[500005];
int tp[200005],s[200005],re[200005];
long long ans,hv1[800005],hv2[800005],mx1[800005],mx2[800005],mx3[800005],ly1[800005],ly2[800005],ly3[800005];
void add(int xx,int yy){l[++tot]=r[xx];d[tot]=yy;r[xx]=tot;
}
void dfs1(int u,int f){fa[u]=f;dep[u]=dep[f]+1;siz[u]=1;for(int i=r[u];i;i=l[i]){if(d[i]==f) continue;dfs1(d[i],u);siz[u]+=siz[d[i]];if(siz[d[i]]>siz[son[u]]) son[u]=d[i];}
}
void dfs2(int u,int f){if(son[u]){tp[son[u]]=tp[u];s[son[u]]=++s[0];re[s[0]]=son[u];dfs2(son[u],u);}for(int i=r[u];i;i=l[i]){if(d[i]==f||d[i]==son[u]) continue;tp[d[i]]=d[i];s[d[i]]=++s[0];re[s[0]]=d[i];dfs2(d[i],u);}
}
void build(int k,int l,int r){if(l==r){hv1[k]=2ll*dep[re[l]]-1;hv2[k]=1ll;return;}int mid=l+r>>1;build(lc,l,mid);build(rc,mid+1,r);hv1[k]=hv1[lc]+hv1[rc];hv2[k]=hv2[lc]+hv2[rc];
}
void down(int k){mx1[lc]+=ly1[k]*hv1[lc];ly1[lc]+=ly1[k];mx2[lc]+=ly2[k]*hv2[lc];ly2[lc]+=ly2[k];mx3[lc]+=ly3[k]*hv2[lc];ly3[lc]+=ly3[k];mx1[rc]+=ly1[k]*hv1[rc];ly1[rc]+=ly1[k];mx2[rc]+=ly2[k]*hv2[rc];ly2[rc]+=ly2[k];mx3[rc]+=ly3[k]*hv2[rc];ly3[rc]+=ly3[k];ly1[k]=ly2[k]=ly3[k]=0;
}
void ch(int k,int l,int r,int x,int y,long long t,int u){if(l>=x&&r<=y){mx1[k]+=t*hv1[k];ly1[k]+=t;mx2[k]+=t*hv2[k];ly2[k]+=t;mx3[k]+=t*dep[u]*hv2[k];ly3[k]+=t*dep[u];return;}if(l>y||r<x) return;if(l==r) return;if(ly1[k]||ly2[k]||ly3[k]) down(k);int mid=l+r>>1;if(x<=mid) ch(lc,l,mid,x,y,t,u);if(y>mid) ch(rc,mid+1,r,x,y,t,u);mx1[k]=mx1[lc]+mx1[rc];mx2[k]=mx2[lc]+mx2[rc];mx3[k]=mx3[lc]+mx3[rc];
}
void find(int k,int l,int r,int x,int y,int u){if(l>=x&&r<=y){ans+=4ll*(mx1[k]-mx2[k]*dep[u]-mx3[k]);return;}if(l>y||r<x) return;if(l==r) return;if(ly1[k]||ly2[k]||ly3[k]) down(k);int mid=l+r>>1;if(x<=mid) find(lc,l,mid,x,y,u);if(y>mid) find(rc,mid+1,r,x,y,u);
}
void ask(int i){int t=i;while(i>=1){find(1,1,s[0],s[tp[i]],s[i],t);i=fa[tp[i]];}
}
void ins(int i){int t=i;while(i>=1){ch(1,1,s[0],s[tp[i]],s[i],1,t);i=fa[tp[i]];}
}
void del(int i){int t=i;while(i>=1){ch(1,1,s[0],s[tp[i]],s[i],-1,t);i=fa[tp[i]];}
}
int main()
{scanf("%d%d",&n,&k);++n;for(int i=1;i<n;i++){scanf("%d%d",&x,&y);++x;++y;add(x,y);add(y,x);}dfs1(1,0);s[1]=++s[0];re[s[0]]=1;tp[1]=1;dfs2(1,0);build(1,1,s[0]);long long sum1=0,sum2=0;for(int i=2,vt,vk=2;i<=n;i++){vt=max(2,i-k);while(vk<vt){sum1-=1ll*dep[vk]*dep[vk];sum2-=1ll*dep[vk];del(vk);++vk;}ans=1ll*(dep[i]-1)*(dep[i]-1)+1ll*(i-vt)*dep[i]*dep[i]+sum1+2ll*dep[i]*sum2;ask(i);printf("%lld\n",ans);sum1+=1ll*dep[i]*dep[i];sum2+=1ll*dep[i];ins(i);}return 0;
}
相关文章:
 T3快速访问)
2021牛客OI赛前集训营-提高组(第四场) T3快速访问
2021牛客OI赛前集训营-提高组(第四场) 题目大意 有一棵n1n1n1个节点的树,根节点为0。给你一个kkk,定义集合Si{j∈Z∣max(1,i−k)≤j<i}∪{0}S_i\{j\in Z|\max(1,i-k)\leq j<i\}\cup\{0\}Si{j∈Z∣max(1,i−k)≤j<i…...
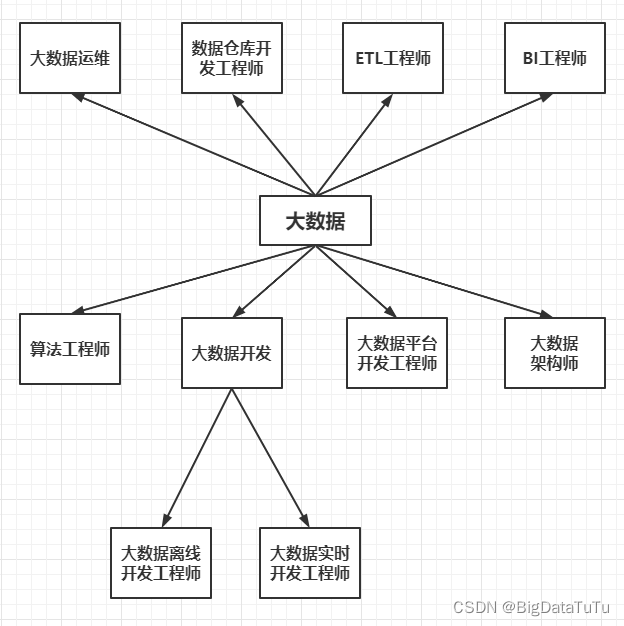
【大数据是什么】
大数据是什么大数据是做什么的?大数据主要有哪些职位 ?大数据运维工程师数据仓库开发工程师ETL工程师大数据开发工程师BI工程师算法工程师大数据平台开发工程师大数据架构师讲述一下自己的大数据学习之路大数据是做什么的? 2014年,…...
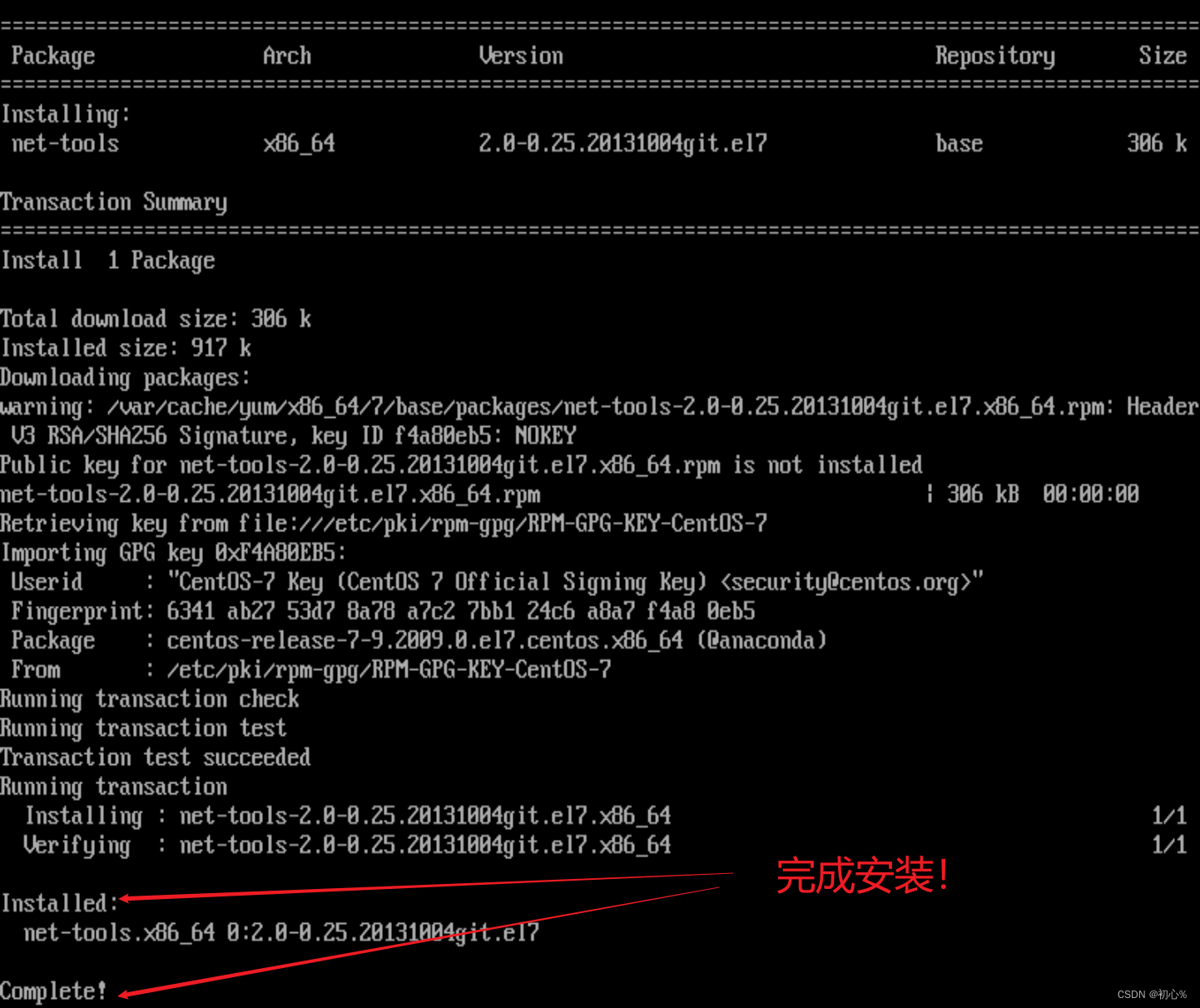
大数据 | centos7图形界面无法执行yum命令
大家好,今天是三八女神节了! 你知道吗?世界上第一位电脑程序设计师是名女性,Ada Lovelace (1815-1852)。 她是一位英国数学家兼作家,第一位主张计算机不只可以用来算数的人,也发表了第一段分析机用的演算…...

三维人脸实践:基于Face3D的渲染、生成与重构 <一>
face3d: Python tools for processing 3D face git code: https://github.com/yfeng95/face3d paper list: PaperWithCode 该方法广泛用于基于三维人脸关键点的人脸生成、属性检测(如位姿、深度、PNCC等),能够快速实现人脸建模与渲染。推荐…...

Javascript 设计模式
设计模式的五大设计原则(SOLID)单一职责:一个程序只需要做好一件事。如果功能过于复杂就拆分开,保证每个部分的独立开放封闭原则:对扩展开放,对修改封闭。增加需求时,扩展新代码,而不是修改源代码。这是软件设计的终极…...
JAVA-文档工具screw-gui
前言 为什么萌生了写文档工具得想法,因为在项目开发得过程中,经常需要补充一些文档,比如数据库文档、详细设计文档等等,文档与项目相绑定,在项目需求新增或变更时,文档也需要反反复复得修改。 1. 数据库…...
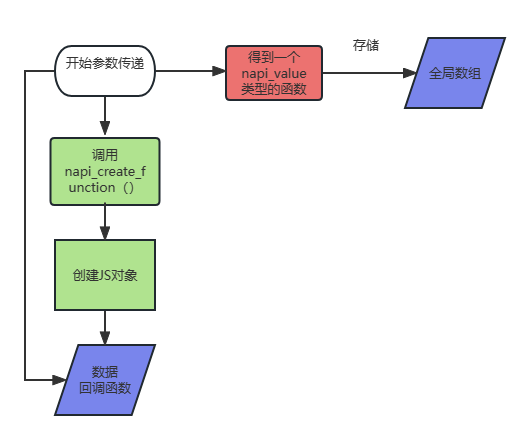
开源鸿蒙南向嵌入学习笔记——NAPI框架学习(一)
开源鸿蒙南向嵌入学习笔记——NAPI框架学习(一) 前言——系列介绍 本系列文章主要是记录笔者在鸿蒙南向的学习与工作中的知识点笔记记录,其中不止会针对鸿蒙中的学习问题进行思考与记录,也会对涉及到的一些嵌入式等其他领域知识&…...
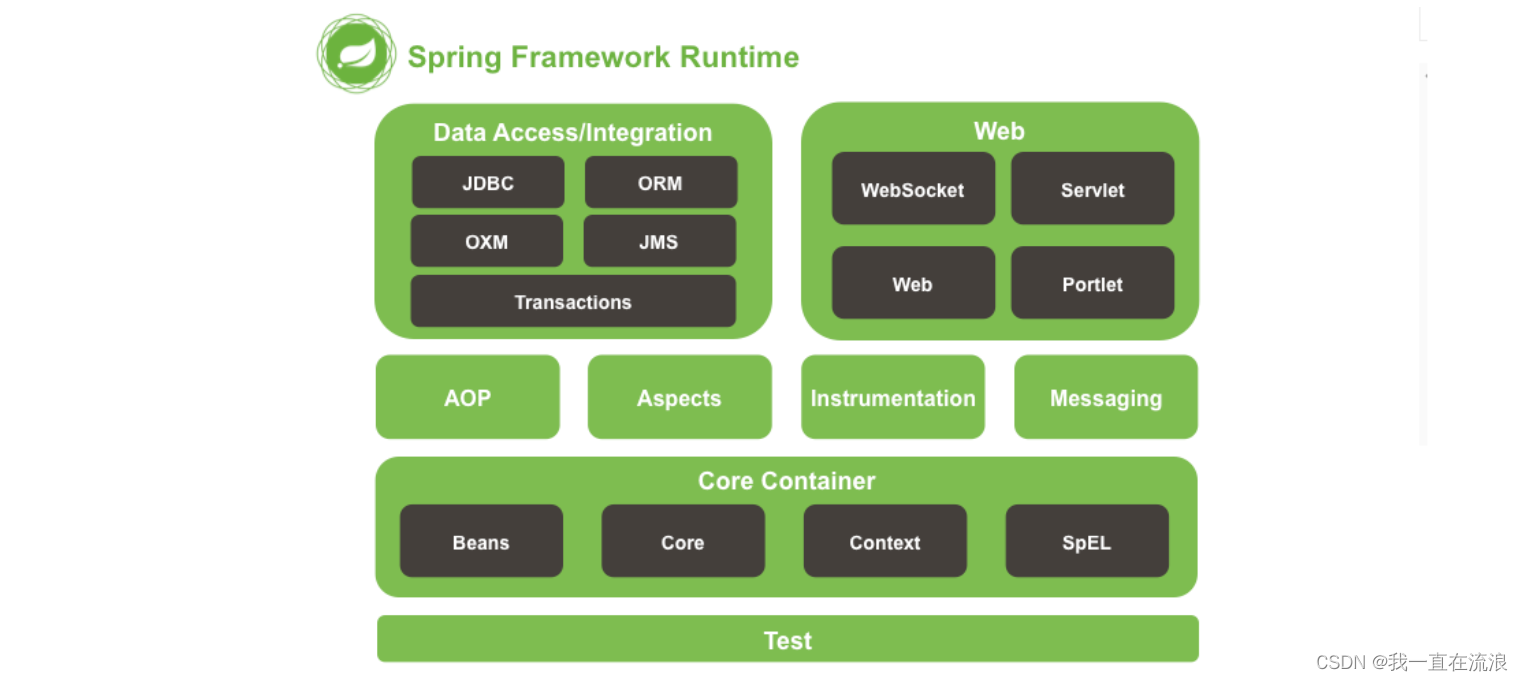
Spring - Spring框架概述面试题总结
文章目录01. 什么是Spring?02. Spring框架的设计目标,设计理念,和核心是什么?03. Spring的优点是什么?04. Spring框架中都用到了哪些设计模式?05. Spring有哪些应用场景?06. Spring由哪些模块组成…...

学习python好就业么
Python的普及与数据挖掘、人工智能和数值计算等领域的蓬勃发展相关,但同时也与普遍编程需求的增加有关。 Python作为人工智能的头号语言,一方面会吸引大量计划从事人工智能的人来学习,另一方面自然也带动了网络上对这门“新语言”的关注和讨…...

瑞幸咖啡的最终目标并不是做国内市场大哥
出品 | 何玺 排版 | 叶媛 日前,瑞幸咖啡发布2022年第四季度及全年财报。数据显示,在刚刚过去的2022年,瑞幸咖啡首次实现了营收超百亿,门店规模也超越老对手星巴克,成为了国内第一连锁咖啡品牌。 那么,瑞幸…...

GPT 模型介绍 | GPT3 / GPT3.5 + Flask | Github源码链接
1. 模型介绍 Chatgpt 使用与 InstructGPT相同的方法,使用来自人类反馈的强化学习 (RLHF) 来训练该模型,但数据收集设置略有不同。我们使用监督微调训练了一个初始模型:人类 AI 训练员提供对话,他们在对话中扮演双方——用户和 AI…...
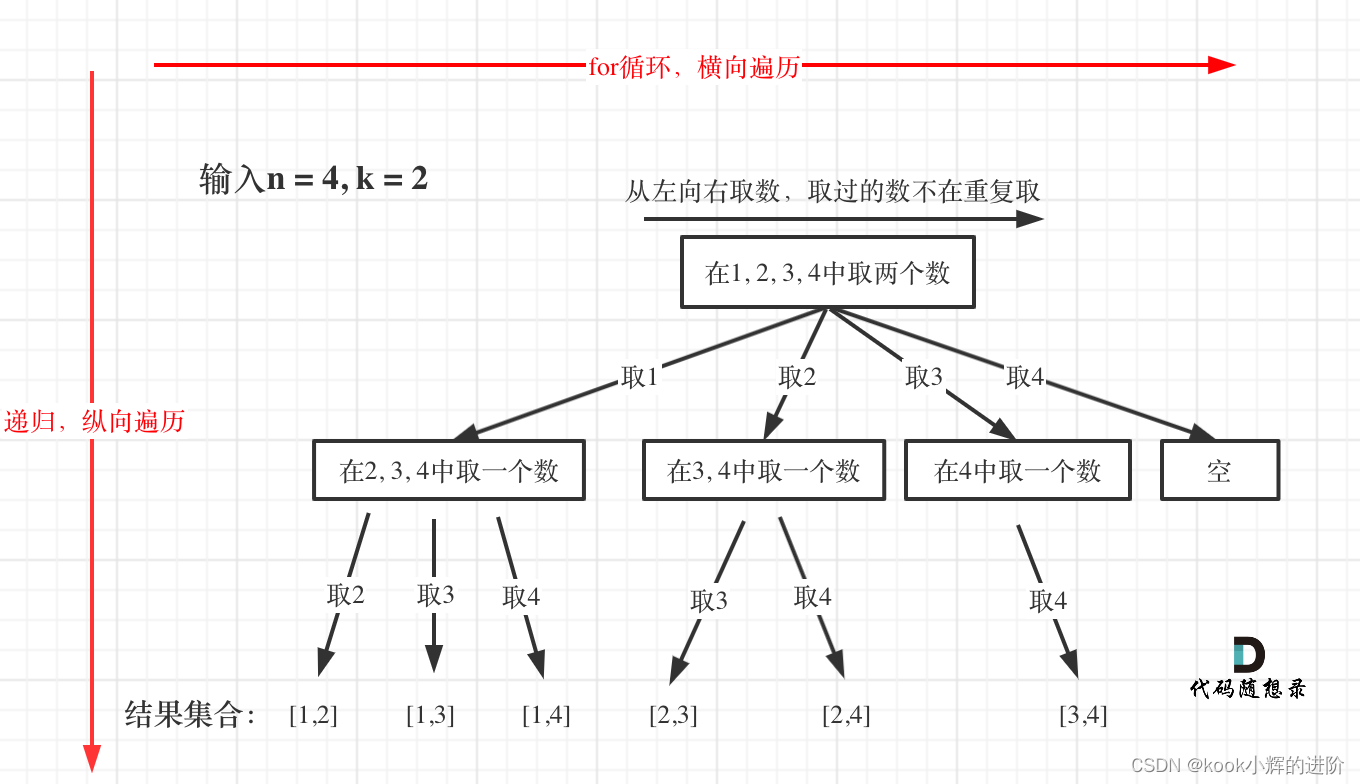
蓝桥杯入门即劝退(二十六)组合问题(回溯算法)
-----持续更新Spring入门系列文章----- 如果你也喜欢Java和算法,欢迎订阅专栏共同学习交流! 你的点赞、关注、评论、是我创作的动力! -------希望我的文章对你有所帮助-------- 专栏:蓝桥杯系列 一、题目描述 给定两个整数 n …...
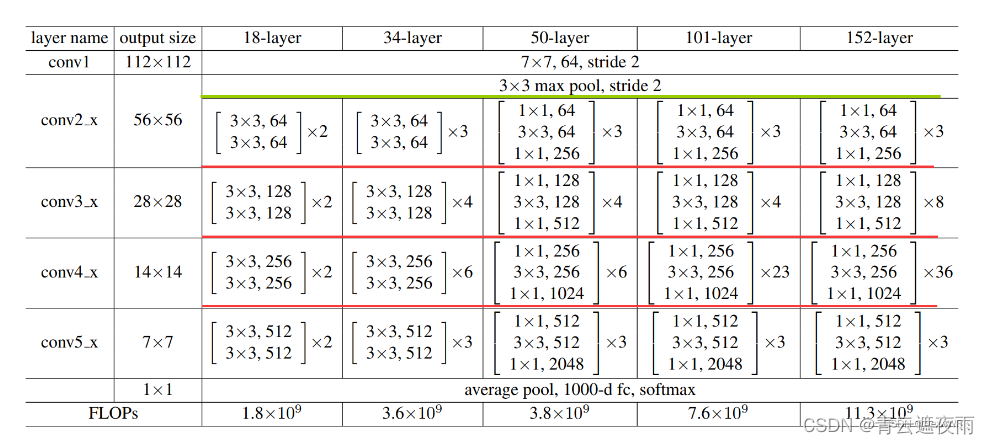
现代卷积神经网络(ResNet)
专栏:神经网络复现目录 本章介绍的是现代神经网络的结构和复现,包括深度卷积神经网络(AlexNet),VGG,NiN,GoogleNet,残差网络(ResNet),稠密连接网络…...
)
PTA:L1-019 谁先倒、L1-020 帅到没朋友、L1-021 重要的话说三遍(C++)
目录 L1-019 谁先倒 问题描述: L1-020 帅到没朋友 问题描述: 实现代码(只过了部分): L1-021 重要的话说三遍 问题描述: 实现代码: 无解析 L1-019 谁先倒 问题描述: 划拳是…...

STL常见容器之set/multiset、map/multimap
set/multiset—集合容器 特点 所有元素都会在插入时自动被排序 本质 set/multiset属于关联式容器,底层结构是二叉树实现 set和multiset区别 set不可以插入重复数据,而multiset可以set插入数据的同时会返回插入结果,表示插入是否成功multiset…...

ThreadLocal 实现原理
每个 Thread 中都存储着一个成员变量:ThreadLocalMap /** InheritableThreadLocal values pertaining to this thread. This map is* maintained by the InheritableThreadLocal class.*/ThreadLocal.ThreadLocalMap inheritableThreadLocals null; ThreadLocal 本…...

BUUCTF [羊城杯 2020]easyre 题解
一.查壳 64位无壳 二.主函数逻辑 可以得知flag长度为38,然后进行三次加密 第一次加密是base64加密,得到code1 第二次加密是将code1拆成四段赋给code2 第三次加密是将code2内的数字和字母移3位,其他字符不变 str2保存的是最终的加密字符 三.encode_one_base64 看到主函数…...

网络协议(十二):HTTPS(SSL/TLS、TLS1.2的连接)
网络协议系列文章 网络协议(一):基本概念、计算机之间的连接方式 网络协议(二):MAC地址、IP地址、子网掩码、子网和超网 网络协议(三):路由器原理及数据包传输过程 网络协议(四):网络分类、ISP、上网方式、公网私网、NAT 网络…...
)
九九乘法表--课后程序(Python程序开发案例教程-黑马程序员编著-第3章-课后作业)
实例9:九九乘法表 乘法口诀是中国古代筹算中进行乘法、除法、开方等运算的基本计算规则,沿用至今已有两千多年。古代的乘法口诀与现在使用的乘法口诀顺序相反,自上而下从“九九八十一”开始到“一一如一”为止,因此,古…...

在超算上安装文件树命令tree
超算平台使用的centos系统没有内置tree命令,需要通过源码安装。记录安装流程如下。 1. 下载源码包 下载链接如下: http://mama.indstate.edu/users/ice/tree/ 选择“Download the latest version” 如本文下载了源码包“tree-2.1.0.tgz”. 2. 源码包…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
)
python爬虫:Newspaper3k 的详细使用(好用的新闻网站文章抓取和解析的Python库)
更多内容请见: 爬虫和逆向教程-专栏介绍和目录 文章目录 一、Newspaper3k 概述1.1 Newspaper3k 介绍1.2 主要功能1.3 典型应用场景1.4 安装二、基本用法2.2 提取单篇文章的内容2.2 处理多篇文档三、高级选项3.1 自定义配置3.2 分析文章情感四、实战案例4.1 构建新闻摘要聚合器…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

RNN避坑指南:从数学推导到LSTM/GRU工业级部署实战流程
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文全面剖析RNN核心原理,深入讲解梯度消失/爆炸问题,并通过LSTM/GRU结构实现解决方案,提供时间序列预测和文本生成…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...

Bean 作用域有哪些?如何答出技术深度?
导语: Spring 面试绕不开 Bean 的作用域问题,这是面试官考察候选人对 Spring 框架理解深度的常见方式。本文将围绕“Spring 中的 Bean 作用域”展开,结合典型面试题及实战场景,帮你厘清重点,打破模板式回答,…...

ubuntu22.04 安装docker 和docker-compose
首先你要确保没有docker环境或者使用命令删掉docker sudo apt-get remove docker docker-engine docker.io containerd runc安装docker 更新软件环境 sudo apt update sudo apt upgrade下载docker依赖和GPG 密钥 # 依赖 apt-get install ca-certificates curl gnupg lsb-rel…...
