递归陷阱七例
目录
栈溢出
无限递归
大常数参数
递归深度过大
重复计算
函数调用开销
递归与迭代的选择
总结
递归是一种强大的编程技术,它允许函数调用自身。递归在很多情况下可以简化代码,使问题更容易理解和解决。然而,递归也容易导致一些常见的问题,这些问题被称为递归陷阱。本文将总结一些常见的递归陷阱,并提供示例代码来避免这些陷阱。
-
栈溢出
递归函数会在每次调用自身时创建一个新的栈帧。如果递归深度过大,可能会导致栈溢出。为了避免栈溢出,我们可以限制递归深度,或者使用尾递归优化。
示例代码:计算斐波那契数列
#include <stdio.h>int fibonacci(int n) {if (n <= 1) {return n;}return fibonacci(n - 1) + fibonacci(n - 2);
}int main() {int n = 10;printf("Fibonacci %d = %d\n", n, fibonacci(n));return 0;
}
在上面的代码中,我们使用递归计算斐波那契数列。然而,这个递归函数的效率很低,因为它会重复计算很多子问题。为了避免栈溢出,我们可以使用动态规划或缓存技术来优化递归函数。
-
无限递归
递归函数必须有终止条件,否则它会无限递归下去。在编写递归函数时,一定要确保有正确的终止条件。
示例代码:计算阶乘
#include <stdio.h>int factorial(int n) {if (n == 0) {return 1;}return n * factorial(n - 1);
}int main() {int n = 5;printf("Factorial %d = %d\n", n, factorial(n));return 0;
}
在上面的代码中,我们使用递归计算阶乘。这个递归函数有一个明确的终止条件:当n等于0时,返回1。这样,递归函数就可以正确地计算出阶乘。
-
大常数参数
递归函数的参数应该尽量小,以减少栈空间的使用。如果递归函数的参数过大,可能会导致栈溢出。
示例代码:计算幂
#include <stdio.h>double power(double x, int n) {if (n == 0) {return 1;}return x * power(x, n - 1);
}int main() {double x = 2.0;int n = 10;printf("%.2f^%d = %.2f\n", x, n, power(x, n));return 0;
}
在上面的代码中,我们使用递归计算幂。然而,这个递归函数的参数n是一个整数,如果n非常大,可能会导致栈溢出。为了避免这个问题,我们可以使用迭代而不是递归。
-
递归深度过大
有些问题本身就需要很深的递归深度才能解决。在这种情况下,我们可以尝试使用非递归算法,或者使用分治法将问题分解成更小的子问题。
示例代码:汉诺塔
#include <stdio.h>void hanoi(int n, char from, char to, char aux) {if (n == 1) {printf("Move disk 1 from %c to %c\n", from, to);return;}hanoi(n - 1, from, aux, to);printf("Move disk %d from %c to %c\n", n, from, to);hanoi(n - 1, aux, to, from);
}int main() {int n = 3;hanoi(n, 'A', 'C', 'B');return 0;
}
在上面的代码中,我们使用递归解决汉诺塔问题。这个问题需要很深的递归深度才能解决。为了避免栈溢出,我们可以限制递归深度,或者使用非递归算法。
-
重复计算
在递归函数中,可能会重复计算相同的子问题多次。为了避免重复计算,我们可以使用记忆化递归(也称为递归+缓存)。
示例代码:计算斐波那契数列(记忆化递归)
#include <stdio.h>
#include <stdlib.h>int *fibCache;int fibonacci(int n) {if (n <= 1) {return n;}if (fibCache[n] != -1) {return fibCache[n];}fibCache[n] = fibonacci(n - 1) + fibonacci(n - 2);return fibCache[n];
}int main() {int n = 10;fibCache = (int *) calloc(n + 1, sizeof(int));for (int i = 0; i <= n; i++) {fibCache[i] = -1;}printf("Fibonacci %d = %d\n", n, fibonacci(n));free(fibCache);return 0;
}
在上面的代码中,我们使用记忆化递归计算斐波那契数列。我们创建了一个缓存数组fibCache来存储已经计算过的斐波那契数。在递归函数中,我们首先检查fibCache[n]是否已经计算过,如果已经计算过,就直接返回结果,否则计算fibCache[n],并将结果存储在fibCache[n]中。
-
函数调用开销
递归函数的每次调用都会有一定的开销,包括参数传递、栈帧创建和销毁等。在递归深度较大时,这些开销可能会累积起来,影响程序的性能。为了避免这个问题,我们可以尝试减少递归深度,或者使用非递归算法。
示例代码:计算幂(迭代)
#include <stdio.h>double power(double x, int n) {double result = 1.0;while (n > 0) {if (n % 2 == 1) {result *= x;}x *= x;n /= 2;}return result;
}int main() {double x = 2.0;int n = 10;printf("%.2f^%d = %.2f\n", x, n, power(x, n));return 0;
}
在上面的代码中,我们使用迭代而不是递归计算幂。这个迭代算法的时间复杂度是O(log n),与递归算法相当,但它避免了递归调用的开销。
-
递归与迭代的选择
在解决某些问题时,递归和迭代都是可行的选择。一般来说,递归更容易理解和实现,但可能会导致性能问题。而迭代可能更难理解和实现,但通常更高效。在选择递归还是迭代时,我们应该根据问题的性质和性能要求来决定。
示例代码:计算斐波那契数列(迭代)
#include <stdio.h>int fibonacci(int n) {int a = 0, b = 1, temp;while (n > 0) {temp = a + b;a = b;b = temp;n--;}return a;
}int main() {int n = 10;printf("Fibonacci %d = %d\n", n, fibonacci(n));return 0;
}
在上面的代码中,我们使用迭代计算斐波那契数列。这个迭代算法的时间复杂度是O(n),与递归算法相当,但它避免了递归调用的开销。
-
总结
递归是一种强大的编程技术,但容易导致一些常见的问题。为了避免递归陷阱,我们应该限制递归深度,使用尾递归优化,确保有正确的终止条件,尽量使用小常数参数,或者使用非递归算法。在编写递归函数时,我们应该仔细考虑这些问题,并选择合适的方法来解决它们。
在本文中,我们讨论了一些常见的递归陷阱,并提供了相应的示例代码。通过理解和避免这些陷阱,我们可以更有效地使用递归来解决各种问题。
相关文章:

递归陷阱七例
目录 栈溢出 无限递归 大常数参数 递归深度过大 重复计算 函数调用开销 递归与迭代的选择 总结 递归是一种强大的编程技术,它允许函数调用自身。递归在很多情况下可以简化代码,使问题更容易理解和解决。然而,递归也容易导致一些常见的…...
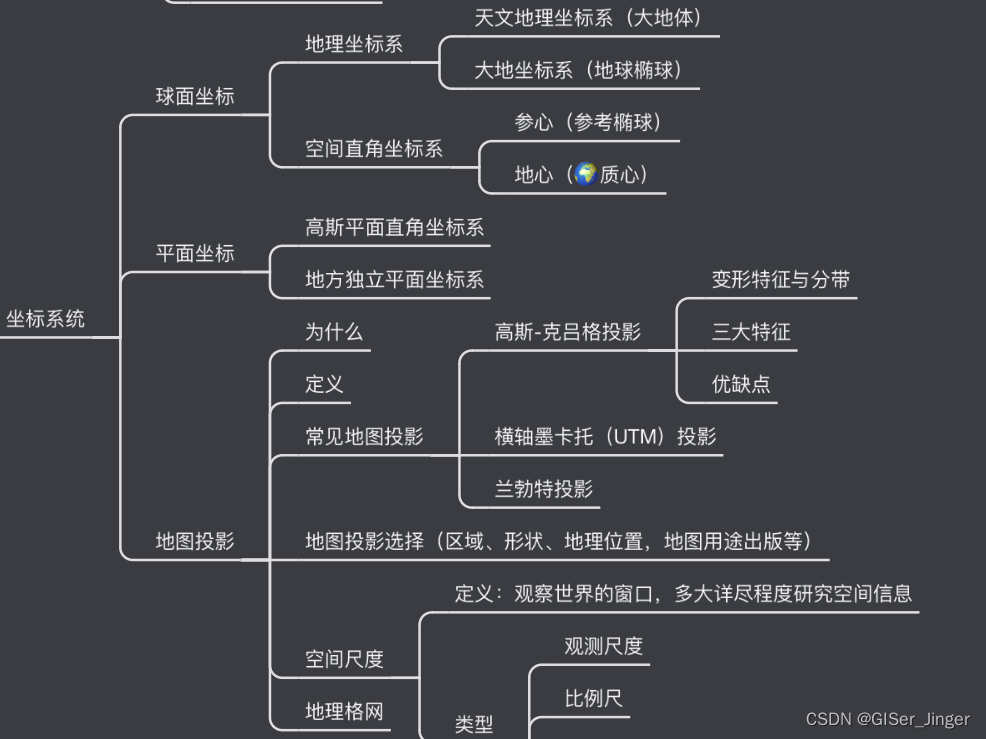
【3D基础】坐标转换——地理坐标投影到平面
汤国安版GIS原理第二章重点 1.常见投影方式 https://download.csdn.net/blog/column/9283203/83387473 Web Mercator投影(Web Mercator Projection): 优点: 在 Web 地图中广泛使用,易于显示并与在线地图服务集成。在…...

颈椎锻炼方式
1. 颈部伸展运动:坐直,慢慢将头向前伸展,直到感到轻微的拉伸,保持数秒钟,然后缓慢放松。重复10次。 2. 颈部旋转运动:坐直,慢慢将头向一侧转动,直到感到轻微的拉伸,保持…...
测试环境搭建:JDK+Tomcat+Mysql+Redis
基础的测试环境搭建: LAMPLinux(CentOS、ubuntu、redhat)ApacheMysqlPHP LTMJLinux(CentOS、ubuntu、redhat)TomcatMysql(Oracle)RedisJava 真实的测试环境搭建:(企业真实的运维) 基于SpringBoot(SpringCloud分布式微…...
 Object Pascal 学习笔记---第11章第1节(混合引用中的错误))
(delphi11最新学习资料) Object Pascal 学习笔记---第11章第1节(混合引用中的错误)
11.1.3 混合引用中的错误 在使用对象时,你通常应该只使用对象变量或接口变量来访问它们。混合使用这两种方法会破坏对象 Pascal 所提供的引用计数机制,并可能导致极难跟踪的内存错误。在实践中,如果你决定使用接口,你可能应该…...
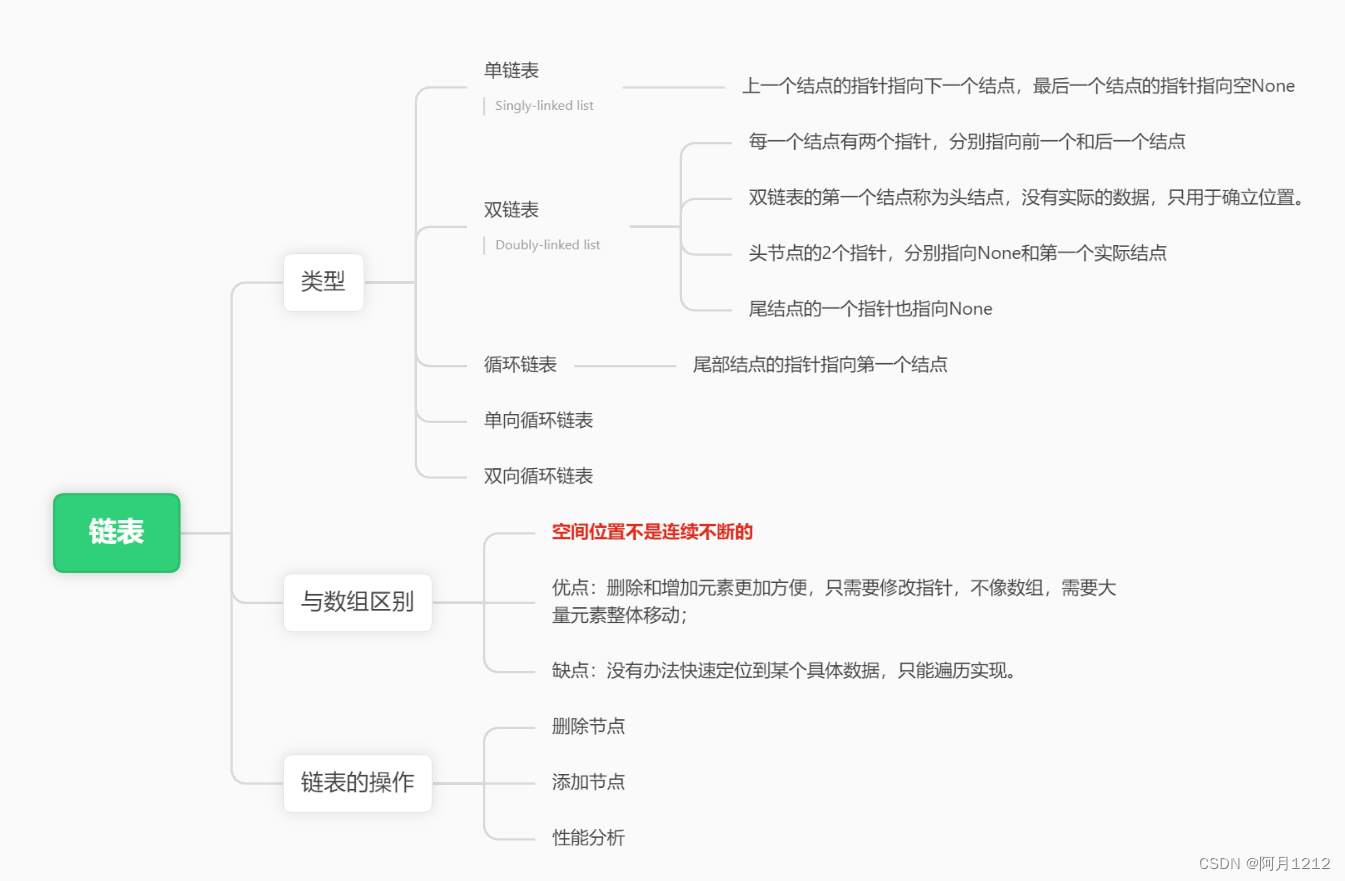
代码随想录算法训练营第三天 | 链表理论基础,203.移除链表元素,707.设计链表,206.反转链表
对于链表完全陌生,但是看题目又觉得和数组一样的 链表理论基础 Q:什么是链表? A:链表是由一系列结点组成的。每一个结点由两部分组成:数据和指针。 203.移除链表元素 题目: 给你一个链表的头节点 head 和…...

如何利用仪表构造InfiniBand流量在数据中心测试中的应用
一、什么是Infiniband? 在当今数据爆炸的时代,数据中心作为信息处理的中心枢纽,面临着前所未有的挑战。传统的通信方式已经难以满足日益增长的数据传输需求,而InfiniBand技术的出现,为数据中心带来了全新的通信解决方…...

Kubernetes 文档 / 概念 / Kubernetes 架构 / 节点
Kubernetes 文档 / 概念 / Kubernetes 架构 / 节点 此文档从 Kubernetes 官网摘录 中文地址 英文地址 节点上的组件包括 kubelet、 容器运行时以及 kube-proxy。 管理 向 API 服务器添加节点的方式主要有两种: 节点上的 kubelet 向控制面执行自注册;…...

ICode国际青少年编程竞赛- Python-1级训练场-for循环练习
ICode国际青少年编程竞赛- Python-1级训练场-for循环练习 1、 for i in range(3):Dev.step(4)Dev.turnLeft()2、 for i in range(3):Dev.step(2)Dev.turnRight()Dev.step(2)Dev.turnLeft()3、 for i in range(3):Dev.step(2)Dev.turnRight()Dev.step(2)Dev.turnLeft()4、 for…...
Flutter分模块开发、模块可单独启动、包含Provider
前言 当前案例 Flutter SDK版本:3.13.2 目前Flutter都是在一个项目中,创建不同目录进行模块开发,我进行Android原生开发时,发现原生端,是可以将每个模块独立运行起来的,灵感来自这; 折腾了几…...

Element-UI快速入门:构建优雅的Vue.js应用界面
Element-UI是一套基于Vue.js的组件库,提供了丰富的UI组件和交互效果,帮助开发者快速构建出美观、功能丰富的Web应用界面。本文将介绍如何快速入门Element-UI,并搭建一个简单的示例界面。 步骤一:安装Element-UI 首先,…...

Flutter 中的 @immutable:深入解析与最佳实践
在 Flutter 开发中,immutable 注释扮演着至关重要的角色,用于标记不可变类。不可变类顾名思义,其状态一旦创建便不可更改,这与可变类截然不同。后者允许在创建后对实例进行修改。 immutable 的利好 引入不可变类可以带来诸多优势…...
Pandas数据可视化 - Matplotlib、Seaborn、Pandas Plot、Plotly
可视化工具介绍 让我们一起探讨Matplotlib、Seaborn、Pandas Plot和Plotly这四个数据可视化库的优缺点以及各自的适用场景。这有助于你根据不同的需求选择合适的工具。 1. Matplotlib 优点: 功能强大:几乎可以用于绘制任何静态、动画和交互式图表。高度可定制&a…...
人工智能的发展将如何重塑网络安全
微信搜索关注公众号网络研究观,获取更多信息。 人们很容易认为人工智能 (AI) 真正出现是在 2019 年,当时 OpenAI 推出了 ChatGPT 的前身 GPT-2。 但现实却有些不同。人工智能的基础可以追溯到 1950 年,当时数学家艾伦图灵发表了题为“计算机…...

Prometheus+Grafana多方位监控
PrometheusGrafana多方位监控 契机 ⚙ 最近发现火山引擎有托管的Prometheus,可是当前是邀测阶段。并且发现火山云的ECS是自带开机自启的exporter的。刚好需要搭建一套服务器监控,所以研究了一套Prometheus监控,包含linux主机监控nginx监控es监控rabbitM…...
使用Docker安装Redis
大家好,今天给大家分享一下如何使用docker安装Redis,关于docker的安装和常用命令,大家可以参考下面两篇文章,本文中不做过多描述。 Docker在Windows与CentOS上的安装 Docker常用命令 关于Redis的介绍与常用操作可以参考&#x…...
(八))
React 之 Effect与事件(event)(八)
Effect(useEffect Hook) 在React中,Effect(或者更具体地说,useEffect Hook)是一个特殊的函数,它允许你在函数组件中执行副作用操作。这些副作用操作可能包括数据获取、手动更改DOM、订阅或取消订…...

网卡的了解
什么是网卡_csdn网卡是什么-CSDN博客 MAC地址:48位串行号(独一无二) 2^48281 474 976 710 656 10位:10亿 5位:1万 15位:10万亿 网卡就是网络适配器 设置--->网络和Internet--->高级网络设置--->硬…...

SSM框架目录
ssm 知识相关目录主要参考尚硅谷 赵伟风老师的视屏,参考链接为 SSM视频_ SSM技术视频_SSM视频教程_尚硅谷 【注意】有些图片为了简便,所以就直接使用了视屏分析。 1、SSM框架相关知识 SpringFramework 基本概念 链接:SpringFramework 基本…...
MATLAB实现杜拉德公式和凯夫公式的计算固液混合料浆临界流速
MATLAB实现杜拉德公式和凯夫公式的计算固液混合料浆临界流速: 杜拉德公式是用来计算非均质固液混合料浆在输送管中的临界速度的公式,具体形式为: uL FL (2gD / (ρ0 - ρ1))^(1/2) 其中: uL:表示料浆的临界速度,…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...

HTML 列表、表格、表单
1 列表标签 作用:布局内容排列整齐的区域 列表分类:无序列表、有序列表、定义列表。 例如: 1.1 无序列表 标签:ul 嵌套 li,ul是无序列表,li是列表条目。 注意事项: ul 标签里面只能包裹 li…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...
基础光照(Basic Lighting))
C++.OpenGL (10/64)基础光照(Basic Lighting)
基础光照(Basic Lighting) 冯氏光照模型(Phong Lighting Model) #mermaid-svg-GLdskXwWINxNGHso {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-GLdskXwWINxNGHso .error-icon{fill:#552222;}#mermaid-svg-GLd…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

ubuntu系统文件误删(/lib/x86_64-linux-gnu/libc.so.6)修复方案 [成功解决]
报错信息:libc.so.6: cannot open shared object file: No such file or directory: #ls, ln, sudo...命令都不能用 error while loading shared libraries: libc.so.6: cannot open shared object file: No such file or directory重启后报错信息&…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...
