【NOI-题解】1586. 扫地机器人1430 - 迷宫出口1434. 数池塘(四方向)1435. 数池塘(八方向)
文章目录
- 一、前言
- 二、问题
- 问题:1586 - 扫地机器人
- 问题:1430 - 迷宫出口
- 问题:1434. 数池塘(四方向)
- 问题:1435. 数池塘(八方向)
- 三、感谢
一、前言
本章节主要对深搜基础题目进行讲解,包括《1586. 扫地机器人》《1430 - 迷宫出口》《1434. 数池塘(四方向)》《1435. 数池塘(八方向)》题目。
二、问题
问题:1586 - 扫地机器人
类型:深度优先搜索
题目描述:
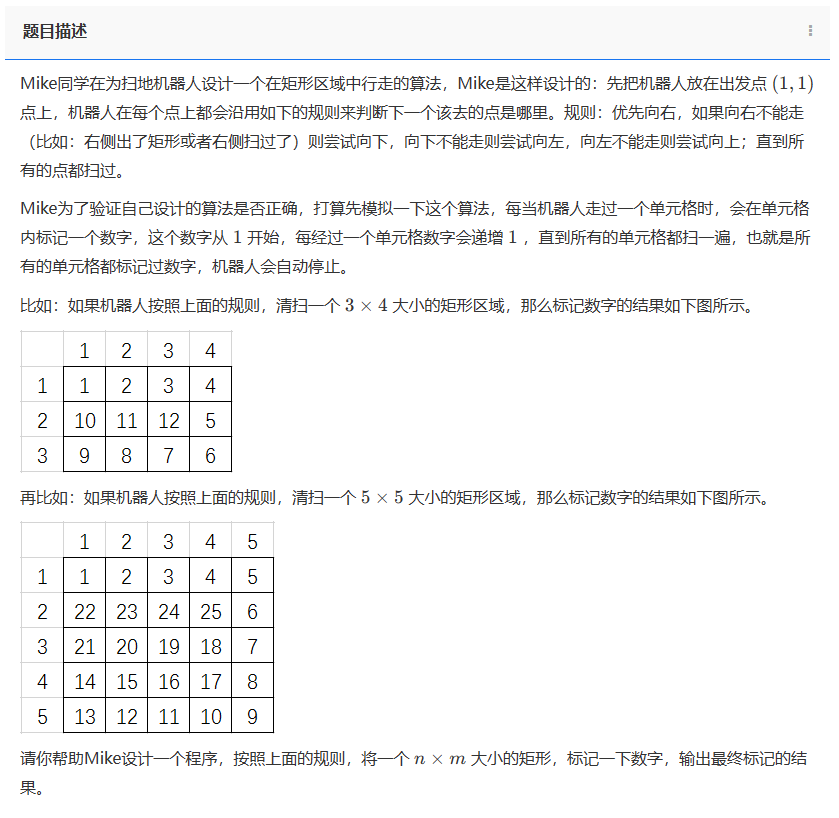
Mike同学在为扫地机器人设计一个在矩形区域中行走的算法,Mike是这样设计的:先把机器人放在出发点
(1,1) 点上,机器人在每个点上都会沿用如下的规则来判断下一个该去的点是哪里。规则:优先向右,如果向右不能走(比如:右侧出了矩形或者右侧扫过了)则尝试向下,向下不能走则尝试向左,向左不能走则尝试向上;直到所有的点都扫过。
Mike为了验证自己设计的算法是否正确,打算先模拟一下这个算法,每当机器人走过一个单元格时,会在单元格内标记一个数字,这个数字从 1 开始,每经过一个单元格数字会递增 1 ,直到所有的单元格都扫一遍,也就是所有的单元格都标记过数字,机器人会自动停止。
输入:
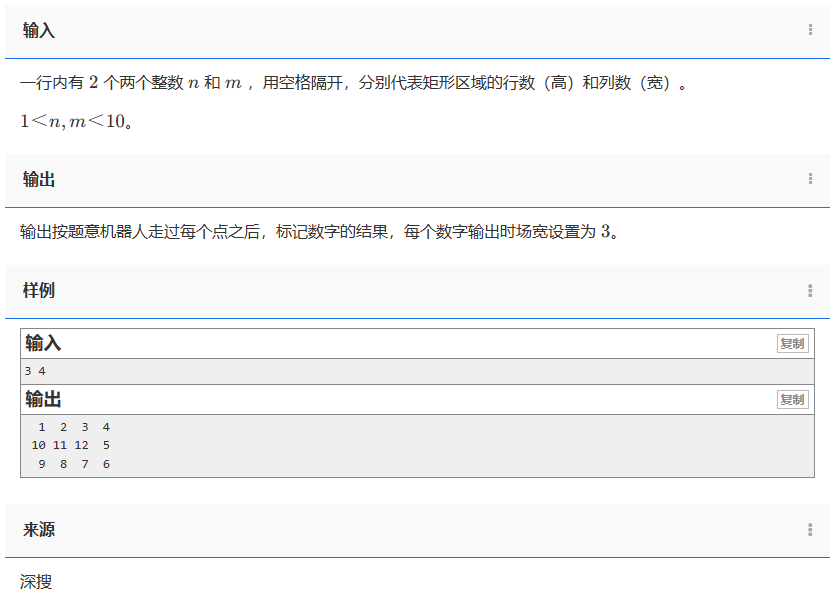
一行内有 2 个两个整数 n 和 m ,用空格隔开,分别代表矩形区域的行数(高)和列数(宽)。
1<n,m<10。
输出:
输出按题意机器人走过每个点之后,标记数字的结果,每个数字输出时场宽设置为 3。
样例:
输入:
3 4
输出:
1 2 3 410 11 12 59 8 7 6
解题思路:
老规矩,首先读题,找出可用条件,过滤无用信息。
可能很多人看到这么长的题目,就不想做了。这也太难了。
看起来本题题目很长,实际上讲了一堆废话。
简单整理一下:

接下来一个一个解决问题。
- 首先n*m的矩形区域。1<n,m<10。
因此直接使用二维数组表示这个地图。
int n,m;
int a[20][20];
- 初始化:先把机器人放在出发点 (1,1) 点上,会在单元格内标记一个数字,这个数字从 1 开始。
那我们需要定义一个递归函数,这个函数的参数除了需要有x,y坐标,还有标记值k。
然后将初始值出发点 (1,1) ,标记值1,传递给递归函数即可。
void dfs(int x,int y,int k){a[x][y]=k;//赋值
}dfs(1,1,1);
- 右、下、左、上的顺序行走。
当选择了一个新的未访问节点后,对该节点进行标记,并递归地调用DFS函数,以该节点作为新的起始点继续探索。这一步是DFS算法递归性的体现,它确保了我们能够深入迷宫的每一个可到达角落。
//右if(y+1<=m && a[x][y+1]==0){dfs(x,y+1,k+1);}//下if(x+1<=n && a[x+1][y]==0){dfs(x+1,y,k+1);} //左if(y-1>=1 && a[x][y-1]==0){dfs(x,y-1,k+1);} //上if(x-1>=1 && a[x-1][y]==0){dfs(x-1,y,k+1);}
那关于这个题目的难点问题就解决完成了。
1.分析问题
- 已知:将一个 n×m 大小的矩形,标记一下数字。
- 未知:输出最终标记的结果。
- 关系:优先向右,如果向右不能走(比如:右侧出了矩形或者右侧扫过了)则尝试向下,向下不能走则尝试向左,向左不能走则尝试向上;直到所有的点都扫过。
2.定义变量
- n 代表二维数组的行数,m 代表列数
- 初始化一个20x20的二维数组,用于存储遍历过程中的标记值
// 全局变量定义
int n, m;
int a[20][20];
3.输入数据
- 输入二维数组的尺寸,即行数n和列数m。
cin >> n >> m;
4.数据计算
- 从二维数组的左上角(1,1)开始进行深度优先搜索,初始标记值为1。
dfs(1, 1, 1);
- 深度优先搜索函数。
void dfs(int x, int y, int k) {// 在当前位置(x, y)标记为ka[x][y] = k;// 检查右方的格子是否在范围内且未被访问过,如果是,则继续深入探索if(y + 1 <= m && a[x][y+1] == 0) {dfs(x, y+1, k+1);}// 检查下方的格子if(x + 1 <= n && a[x+1][y] == 0) {dfs(x+1, y, k+1);} // 检查左方的格子if(y - 1 >= 1 && a[x][y-1] == 0) {dfs(x, y-1, k+1);} // 检查上方的格子if(x - 1 >= 1 && a[x-1][y] == 0) {dfs(x-1, y, k+1);}
}
5.输出结果
- 输出遍历后的二维数组,展示每个格子被访问的顺序。
for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {// 使用setw(3)设置输出宽度,保持输出对齐美观cout << setw(3) << a[i][j];}// 每行输出结束后换行cout << endl;}
完整代码如下:
#include<bits/stdc++.h> // 引入标准库中的所有常用头文件,简化编程时的头文件包含
using namespace std; // 使用std命名空间,可以直接调用std中的函数和对象,无需前缀// 全局变量定义
int n, m; // n 代表二维数组的行数,m 代表列数
int a[20][20]; // 初始化一个20x20的二维数组,用于存储遍历过程中的标记值// 深度优先搜索函数
void dfs(int x, int y, int k) {// 在当前位置(x, y)标记为ka[x][y] = k;// 检查右方的格子是否在范围内且未被访问过,如果是,则继续深入探索if(y + 1 <= m && a[x][y+1] == 0) {dfs(x, y+1, k+1);}// 检查下方的格子if(x + 1 <= n && a[x+1][y] == 0) {dfs(x+1, y, k+1);} // 检查左方的格子if(y - 1 >= 1 && a[x][y-1] == 0) {dfs(x, y-1, k+1);} // 检查上方的格子if(x - 1 >= 1 && a[x-1][y] == 0) {dfs(x-1, y, k+1);}
}int main() {// 主函数开始// 用户输入二维数组的尺寸,即行数n和列数mcin >> n >> m;// 从二维数组的左上角(1,1)开始进行深度优先搜索,初始标记值为1dfs(1, 1, 1);// 输出遍历后的二维数组,展示每个格子被访问的顺序for(int i = 1; i <= n; i++) {for(int j = 1; j <= m; j++) {// 使用setw(3)设置输出宽度,保持输出对齐美观cout << setw(3) << a[i][j];}// 每行输出结束后换行cout << endl;}// 程序结束,返回0表示成功执行return 0;
}
解法二
解题思路:使用方向数组
在解决迷宫问题时,方向数组用于指导搜索算法(如深度优先搜索、广度优先搜索)探索相邻的可通行格子。例如,从当前格子出发,按照方向数组中指定的偏移量,检查上下左右(或更多方向)的格子是否可通行,并决定下一步的移动方向。
通常情况下,迷宫问题中采用的坐标系与数学上的笛卡尔坐标系有所不同,通常约定:
- y 表示横向(列),从左到右递增。
- 表示纵向(行),从上到下递增。
按照这样的约定,迷宫中四个基本方向的坐标增量应为:
右(0, 1)
下(1, 0)
左(0, -1)
上(-1, 0)
示例:
以下是一个二维空间中表示四个基本方向(上、下、左、右)的方向数组:
int directions[4][2] = {{-1, 0}, // 上:向负x方向移动,y坐标不变{1, 0}, // 下:向正x方向移动,y坐标不变{0, -1}, // 左:向负y方向移动,x坐标不变{0, 1} // 右:向正y方向移动,x坐标不变
};
当然也可以使用一维数组表示:
右(0, 1)、下(1, 0)、左(0, -1)、上(-1, 0)。
int fx[5]={0,0,1,0,-1};
int fy[5]={0,1,0,-1,0};
完整代码如下:
#include <bits/stdc++.h>
using namespace std;// 定义全局变量
int n, m; // 矩形网格的行数(n)和列数(m)
int a[20][20]; // 用于存储每个格子的标记值的二维数组,大小为 n × m// 定义方向数组,存储x和y坐标变化的值
int fx[5] = {0, 0, 1, 0, -1}; // 右(0, 1)、下(1, 0)、左(0, -1)、上(-1, 0)
int fy[5] = {0, 1, 0, -1, 0};// 深度优先搜索(DFS)函数
// 参数:当前格子的坐标 x, y,当前标记值 k
void dfs(int x, int y, int k) {// 将当前格子 (x, y) 的标记值更新为 ka[x][y] = k;// 遍历四个方向(右、下、左、上),按照索引 i(1~4)for (int i = 1; i <= 4; i++) {// 计算下一个待访问格子的坐标 tx 和 tyint tx = x + fx[i];int ty = y + fy[i];// 递归之前先判断,确保要访问的点的有效性// (1)坐标在矩形范围内:1 <= tx <= n 且 1 <= ty <= m// (2)该格子尚未被访问过:a[tx][ty] == 0if (tx >= 1 && tx <= n && ty >= 1 && ty <= m && a[tx][ty] == 0) {// 若满足条件,递归调用 dfs 函数,继续标记下一个格子dfs(tx, ty, k + 1);}}
}int main() {// 一、分析问题// 已知:将一个 n×m 大小的矩形,标记一下数字。// 未知:输出最终标记的结果。// 关系:优先向右,如果向右不能走(比如:右侧出了矩形或者右侧扫过了)则尝试向下,// 向下不能走则尝试向左,向左不能走则尝试向上;直到所有的点都扫过。// 二、数据定义// 已在全局变量中定义// 三、数据输入cin >> n >> m;// 四、数据计算// 为(1,1)点赋值为1dfs(1, 1, 1);// 五、输出结果for (int i = 1; i <= n; i++) {for (int j = 1; j <= m; j++) {// 输出每个格子的标记值,格式化输出宽度为3cout << setw(3) << a[i][j];}// 每行输出结束后换行cout << endl;}return 0;
}
问题:1430 - 迷宫出口
类型:深搜 递归 广搜
题目描述:
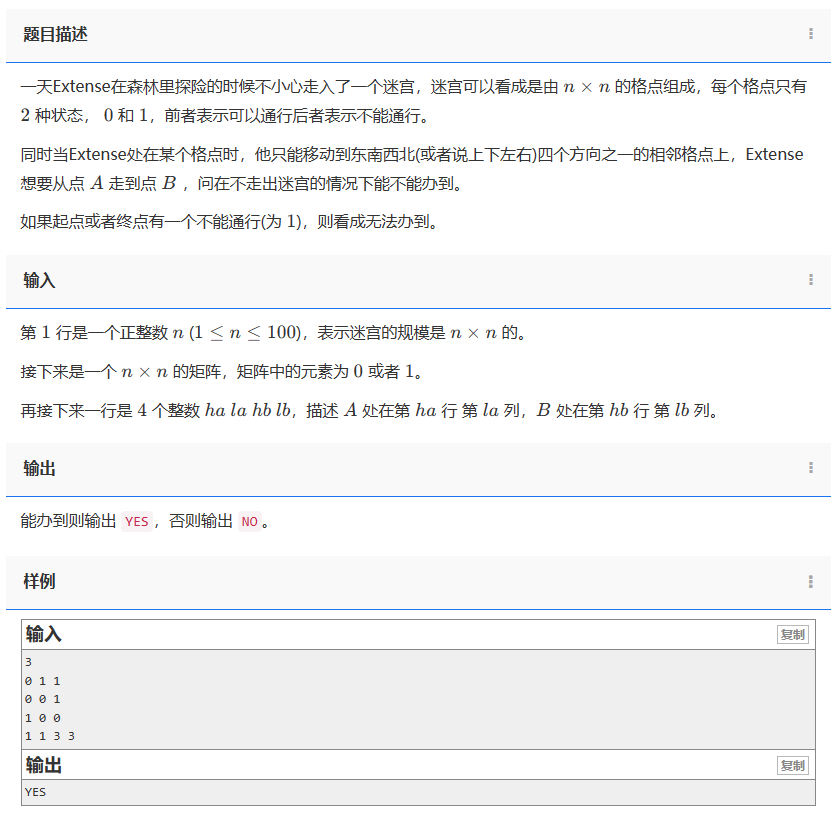
一天Extense在森林里探险的时候不小心走入了一个迷宫,迷宫可以看成是由 n×n 的格点组成,每个格点只有 2 种状态, 0 和 1,前者表示可以通行后者表示不能通行。
同时当Extense处在某个格点时,他只能移动到东南西北(或者说上下左右)四个方向之一的相邻格点上,Extense想要从点 A 走到点 B ,问在不走出迷宫的情况下能不能办到。
如果起点或者终点有一个不能通行(为 1),则看成无法办到。
输入:
第 1 行是一个正整数 n (1≤n≤100),表示迷宫的规模是 n×n 的。
接下来是一个n×n 的矩阵,矩阵中的元素为 0 或者 1。
再接下来一行是 4 个整数 ha la hb lb,描述 A 处在第 ha 行 第 la 列,B 处在第 hb 行 第lb 列。
输出:
能办到则输出 YES,否则输出 NO。
样例:
输入:
3
0 1 1
0 0 1
1 0 0
1 1 3 3
输出:
YES
解题思路:
本题是问有一个n*n的迷宫,从点 A 走到点 B ,问在不走出迷宫的情况下能不能办到。
那如何判断是否存在这一条路径是解题的关键。
其实可以像上一题一样,让点A移动,如果点A的坐标和点B的坐标重合,那就意味着存在这么一条路径。
并且本题只是问了是否存在点A到点B的路径,因此只要找到1条就可以了。
1.分析问题
- 已知:n*n的迷宫 ,每个格点只有 2 种状态, 0 和 1,前者表示可以通行后者表示不能通行。
- 未知:从点 A 走到点 B ,问在不走出迷宫的情况下能不能办到。
- 关系:如果起点或者终点有一个不能通行(为 1),则看成无法办到。
2.定义变量
- 整型变量 n 存储迷宫的边长(假设为正方形迷宫)。
- 整型变量 ha、la、hb、lb 分别存储起点和终点的行、列坐标。
- 定义一个 n × n 的二维整型数组 mg,用于存储迷宫的格子状态,其中0表示可通行,1表示不可通行。
- 布尔变量 pathFound 用于记录是否找到了从起点到终点的路径。
- 定义两个一维整型数组 fx 和 fy,分别存储在遍历时x轴和y轴方向的变化值。这里定义了四个基本方向。
//二、数据定义
int n;
int ha,la,hb,lb;
int mg[110][110];
bool pathFound =false;int fx[5]={0,0,1,0,-1};
int fy[5]={0,1,0,-1,0};
3.输入数据
- 输入迷宫的边长 n 和迷宫数据。
- 输入起点和终点坐标。
//三、数据输入 cin>>n;for(int i=1;i<=n;i++){for(int j=1;j<=n;j++){cin>>mg[i][j];}} cin>>ha>>la>>hb>>lb;
4.数据计算
- 检查起点或终点是否不可通行(值为1)。若任意一个不可通行,输出 “NO”,表示无法从起点走到终点。
- 若起点和终点均可通行,调用 dfs(ha, la) 进行深度优先搜索。
- 根据 pathFound 的值输出结果:
若 pathFound 为 true,输出 “YES”,表示找到了从起点到终点的路径。
若 pathFound 仍为 false,输出 “NO”,表示未能找到从起点到终点的路径。
//四、数据计算 //如果起点或者终点有一个不能通行(为 1),则看成无法办到if(mg[ha][la]==1 || mg[hb][lb]==1){//五、输出结果cout<<"NO";}else{dfs(ha,la); if(pathFound){//五、输出结果cout<<"YES";}else{//五、输出结果cout<<"NO";}
- 函数 dfs(x, y) 接收当前格子的坐标 x 和 y。
- 首先将当前格子 mg[x][y] 标记为已访问(值为1)。
- 使用两个变量 tx 和 ty 存储下一个待探索格子的坐标。
- 循环遍历方向数组 fx 和 fy,依次尝试向右、下、左、上移动。
- 计算下一个待探索格子的坐标 tx 和 ty。
- 检查新坐标是否有效(即位于迷宫范围内且未被访问过):
如果有效且到达终点 (tx == hb 且 ty == lb),将 pathFound 设为 true 并结束搜索。
如果有效且未到达终点,递归调用 dfs(tx, ty) 继续探索下一个格子。 - 递归结束后,若 pathFound 仍为 false,说明从当前格子出发无法到达终点。
void dfs(int x,int y){mg[x][y]=1;//走过的路进行标记int tx,ty;//表示要探索的点for(int i=1;i<=4;i++){tx=x+fx[i];ty=y+fy[i];if(tx>=1&&tx<=n&&ty>=1&&ty<=n&&mg[tx][ty]==0){if(tx==hb&&ty==lb){pathFound=true;}else{dfs(tx,ty);}}}
}
完整代码如下:
#include <iostream>
using namespace std;// 二、数据定义
int n; // 迷宫的边长(假设为正方形迷宫)
int ha, la, hb, lb; // 起点和终点的行、列坐标
int mg[110][110]; // 用于存储迷宫的格子状态,0表示可通行,1表示不可通行
bool pathFound = false; // 记录是否找到了从起点到终点的路径// 方向数组,存储x和y坐标变化的值,符合迷宫问题中约定的坐标系
int fx[5] = {0, 0, 1, 0, -1}; // 右(0, 1)、下(1, 0)、左(0, -1)、上(-1, 0)
int fy[5] = {0, 1, 0, -1, 0};// 深度优先搜索(DFS)函数
// 参数:当前格子的坐标 x, y
void dfs(int x, int y) {mg[x][y] = 1; // 将当前格子标记为已访问(值为1)int tx, ty; // 表示要探索的点// 遍历四个方向(右、下、左、上),按照索引 i(1~4)for (int i = 1; i <= 4; i++) {tx = x + fx[i];ty = y + fy[i];// 检查新坐标是否有效(即位于迷宫范围内且未被访问过)if (tx >= 1 && tx <= n && ty >= 1 && ty <= n && mg[tx][ty] == 0) {// 若有效且到达终点,将 pathFound 设为 true 并结束搜索if (tx == hb && ty == lb) {pathFound = true;break;}// 若有效且未到达终点,递归调用 dfs 继续探索下一个格子else {dfs(tx, ty);}}}
}int main() {// 一、分析问题// 已知:n × n 的迷宫,每个格点只有 2 种状态,0 和 1,前者表示可以通行,后者表示不能通行。// 未知:从点 A 走到点 B,问在不走出迷宫的情况下能不能办到。// 关系:如果起点或者终点有一个不能通行(为 1),则看成无法办到。// 二、数据定义// 已在全局变量中定义// 三、数据输入cin >> n;for (int i = 1; i <= n; i++) {for (int j = 1; j <= n; j++) {cin >> mg[i][j];}}cin >> ha >> la >> hb >> lb;// 四、数据计算// 如果起点或者终点有一个不能通行(为 1),则看成无法办到if (mg[ha][la] == 1 || mg[hb][lb] == 1) {// 五、输出结果cout << "NO";} else {dfs(ha, la); // 执行深度优先搜索if (pathFound) {// 五、输出结果cout << "YES";} else {// 五、输出结果cout << "NO";}}return 0;
}
问题:1434. 数池塘(四方向)
类型:深搜
题目描述:
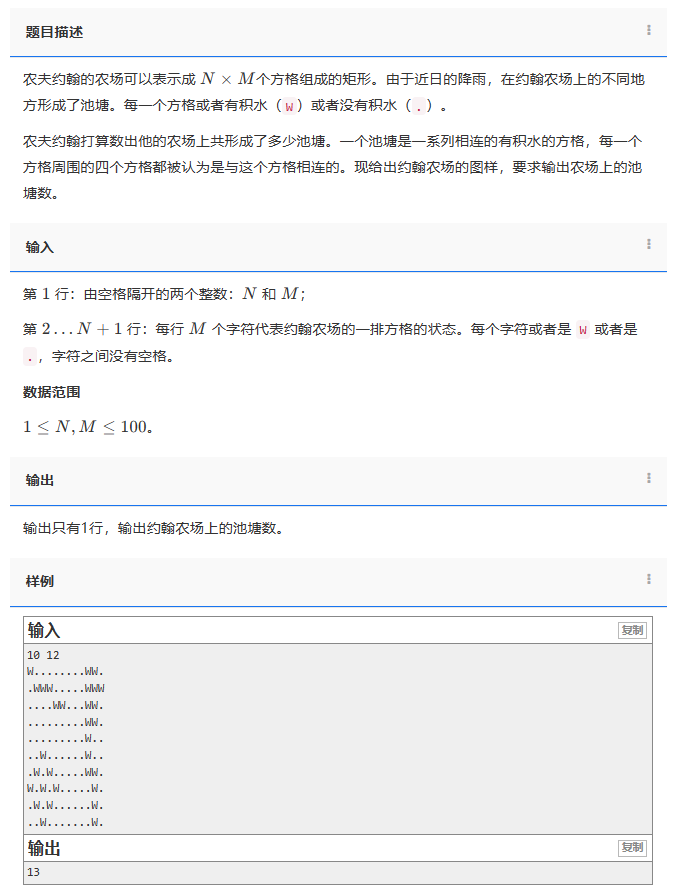
农夫约翰的农场可以表示成 N×M个方格组成的矩形。由于近日的降雨,在约翰农场上的不同地方形成了池塘。每一个方格或者有积水(W)或者没有积水(.)。
农夫约翰打算数出他的农场上共形成了多少池塘。一个池塘是一系列相连的有积水的方格,每一个方格周围的四个方格都被认为是与这个方格相连的。现给出约翰农场的图样,要求输出农场上的池塘数。
输入:
第 1 行:由空格隔开的两个整数:N 和 M;
第 2…N+1 行:每行 M 个字符代表约翰农场的一排方格的状态。每个字符或者是 W 或者是 .,字符之间没有空格。
数据范围1≤N,M≤100。
输出:
输出只有1行,输出约翰农场上的池塘数。
样例:
输入:
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
输出:
13
解题思路:
本题是给定一个n*m的二维网格地图,每个格子要么是积水(标记为字符’W’),要么是无水区域(标记为字符’.')。要求计算出地图上的池塘(由相邻的积水格子组成)总数。
那我们可以遍历这个n*m的方格,来判断这个方格是积水还是无水。
如果当前脚下的格子是积水,那么采用深度优先搜索(DFS)遍历每个积水格子,并将其标记为已访问(避免重复计数),同时递归地访问其上下左右的相邻积水格子。每当开始一个新的DFS过程,就说明发现了一个新的池塘,池塘计数加一。
FOR 每一行 i 从 1 到 n(包括n)FOR 每一列 j 从 1 到 m(包括m)IF 当前格子 farm[i][j] 是积水 ('W')调用深度优先搜索函数 dfs(i, j),从当前位置开始探索相连的积水区域池塘计数器 c 加一,表示发现一个新的池塘END IFEND FOR
END FOR
关于dfs函数在上面已经介绍,选用其中一种方法即可。
1.分析问题
- 已知:n*m的矩形 ,农场的方格的状态有积水(W)或者没有积水(.) 。
- 未知:池塘数量c。
- 关系:深搜
2.定义变量
- 全局变量定义,方便函数调用。
- n, m 分别代表二维网格的行数和列数。
- farm[110][110] 用来存储地图状态,‘W’ 表示积水,‘.’ 表示无水。
int n,m, farm[110][110];
- c 用来记录池塘的数量。
//二、定义变量(已知、未知、关系)int c=0;
3.输入数据
- 首先读取地图的尺寸n和m。
- 接着,通过两层循环读取每个格子的状态,并存储到farm数组中。
//三、输入已知cin>>n>>m;for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){char a;cin>>a;farm[i][j]=a;}}
4.数据计算
- 一个两层循环遍历地图的每个格子。
- 如果当前格子为积水,调用dfs函数,并增加池塘计数c。
//四、根据关系计算for(int i=1;i<=n;i++){for(int j=1;j<=m;j++){if(farm[i][j]=='W'){dfs(i,j);++c;}}}
- dfs函数实现了深度优先搜索,当遇到边界或非积水格子时返回,否则继续深入探索四周的格子,并将访问过的积水格子标记为.。
void dfs(int x,int y){if(x<1||x>n||y<1||y>m||farm[x][y]!='W'){return;}farm[x][y]='.';dfs(x,y+1);dfs(x+1,y);dfs(x,y-1);dfs(x-1,y);}
5.输出结果
- 最后,输出池塘的总数量c。
//五、输出未知 cout<<c;return 0;
完整代码如下:
#include<bits/stdc++.h> // 包含大量常用头文件的预处理指令
using namespace std; // 使用std命名空间,简化标准库的使用// 全局变量定义
int n, m; // n为行数,m为列数
int farm[110][110]; // 用于存储农场地图状态的二维数组// 深度优先搜索函数,用于遍历并标记相连的积水区域
void dfs(int x, int y){// 判断当前位置是否越界或非积水区域,若是则返回if(x < 1 || x > n || y < 1 || y > m || farm[x][y] != 'W'){return;}// 将当前积水区域标记为已访问(即无水区域)farm[x][y] = '.';// 递归地访问当前位置的上、下、左、右四个相邻格子dfs(x, y+1); // 右dfs(x+1, y); // 下dfs(x, y-1); // 左dfs(x-1, y); // 上
}int main(){// 初始化池塘计数器int c = 0; // 输入农场的尺寸cin >> n >> m;// 根据输入构建农场地图for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){char a; // 临时变量存储输入字符cin >> a; // 读取当前位置的状态farm[i][j] = a; // 将状态存储到二维数组中}}// 遍历地图,使用DFS寻找并标记所有池塘for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){// 若当前位置为积水,则启动DFS,同时池塘计数加一if(farm[i][j] == 'W'){dfs(i, j);++c;}}}// 输出最终的池塘数量cout << c;return 0; // 主函数正常结束
}
问题:1435. 数池塘(八方向)
类型:深搜
题目描述:
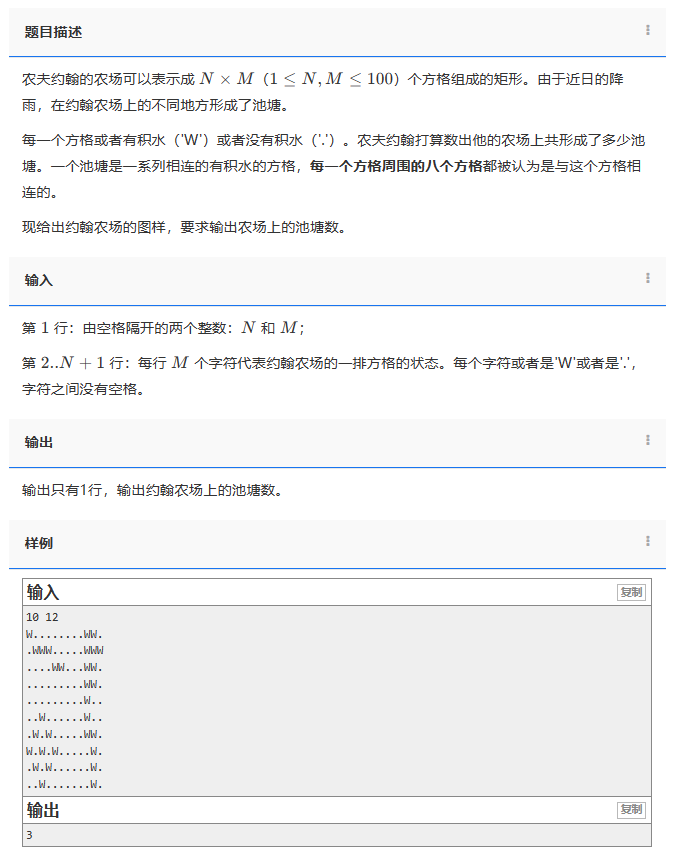
农夫约翰的农场可以表示成 N×M(1≤N,M≤100)个方格组成的矩形。由于近日的降雨,在约翰农场上的不同地方形成了池塘。
每一个方格或者有积水(‘W’)或者没有积水(‘.’)。农夫约翰打算数出他的农场上共形成了多少池塘。一个池塘是一系列相连的有积水的方格,每一个方格周围的八个方格都被认为是与这个方格相连的。
现给出约翰农场的图样,要求输出农场上的池塘数。
输入:
第 1 行:由空格隔开的两个整数:N 和 M;
第 2…N+1 行:每行 M 个字符代表约翰农场的一排方格的状态。每个字符或者是 W 或者是 .,字符之间没有空格。
数据范围1≤N,M≤100。
输出:
输出只有1行,输出约翰农场上的池塘数。
样例:
输入:
10 12
W........WW.
.WWW.....WWW
....WW...WW.
.........WW.
.........W..
..W......W..
.W.W.....WW.
W.W.W.....W.
.W.W......W.
..W.......W.
输出:
3
解题思路
作为上一题的延申,进一步验证对角线上的方格即可。
完整代码如下:
#include <bits/stdc++.h> // 包含常用的STL库和一些优化的头文件
using namespace std; // 使用std命名空间,简化代码中的库函数调用// 全局变量声明
int n, m; // 分别表示农场的行数和列数
int farm[110][110]; // 二维数组用于存储农场的状态,'W'表示积水,'.'表示无积水// 深度优先搜索函数,用于遍历相连的积水区域
void dfs(int x, int y){// 检查坐标是否越界或当前位置是否为非积水区域,若是则直接返回if(x < 1 || x > n || y < 1 || y > m || farm[x][y] != 'W'){return;}// 将当前积水位置标记为已访问(无积水状态)farm[x][y] = '.';// 递归地探索当前点上下左右及对角线方向的相邻点dfs(x, y+1); // 右dfs(x+1, y); // 下dfs(x, y-1); // 左dfs(x-1, y); // 上dfs(x+1, y+1); // 右下dfs(x-1, y+1); // 左下dfs(x+1, y-1); // 右上dfs(x-1, y-1); // 左上
}int main(){// 问题分析、变量定义与输入处理// 未知数:池塘数量cint c = 0; // 输入农场的尺寸cin >> n >> m;// 输入农场的状态,存储到farm数组中for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){char a;cin >> a;farm[i][j] = a;}}// 计算过程:遍历农场,使用DFS发现并标记所有池塘for(int i = 1; i <= n; i++){for(int j = 1; j <= m; j++){if(farm[i][j] == 'W'){ // 如果当前位置是积水dfs(i, j); // 对该位置进行DFS遍历++c; // 每次DFS完成,表示发现一个新的池塘,计数器加一}}}// 输出结果:池塘的总数量cout << c;return 0; // 程序正常结束
}
三、感谢
如若本文对您的学习或工作有所启发和帮助,恳请您给予宝贵的支持——轻轻一点,为文章点赞;若觉得内容值得分享给更多朋友,欢迎转发扩散;若认为此篇内容具有长期参考价值,敬请收藏以便随时查阅。
每一次您的点赞、分享与收藏,都是对我持续创作和分享的热情鼓励,也是推动我不断提供更多高质量内容的动力源泉。期待我们在下一篇文章中再次相遇,共同攀登知识的高峰!

相关文章:

【NOI-题解】1586. 扫地机器人1430 - 迷宫出口1434. 数池塘(四方向)1435. 数池塘(八方向)
文章目录 一、前言二、问题问题:1586 - 扫地机器人问题:1430 - 迷宫出口问题:1434. 数池塘(四方向)问题:1435. 数池塘(八方向) 三、感谢 一、前言 本章节主要对深搜基础题目进行讲解…...

探究MySQL行格式:解析DYNAMIC与COMPACT的异同
在MySQL中,行格式对于数据存储和检索起着至关重要的作用。MySQL提供了多种行格式,其中DYNAMIC和COMPACT是两种常见的行格式。 本文将深入探讨MySQL行格式DYNAMIC和COMPACT的区别,帮助读者更好地理解它们的特点和适用场景。 1. MySQL行格式简…...
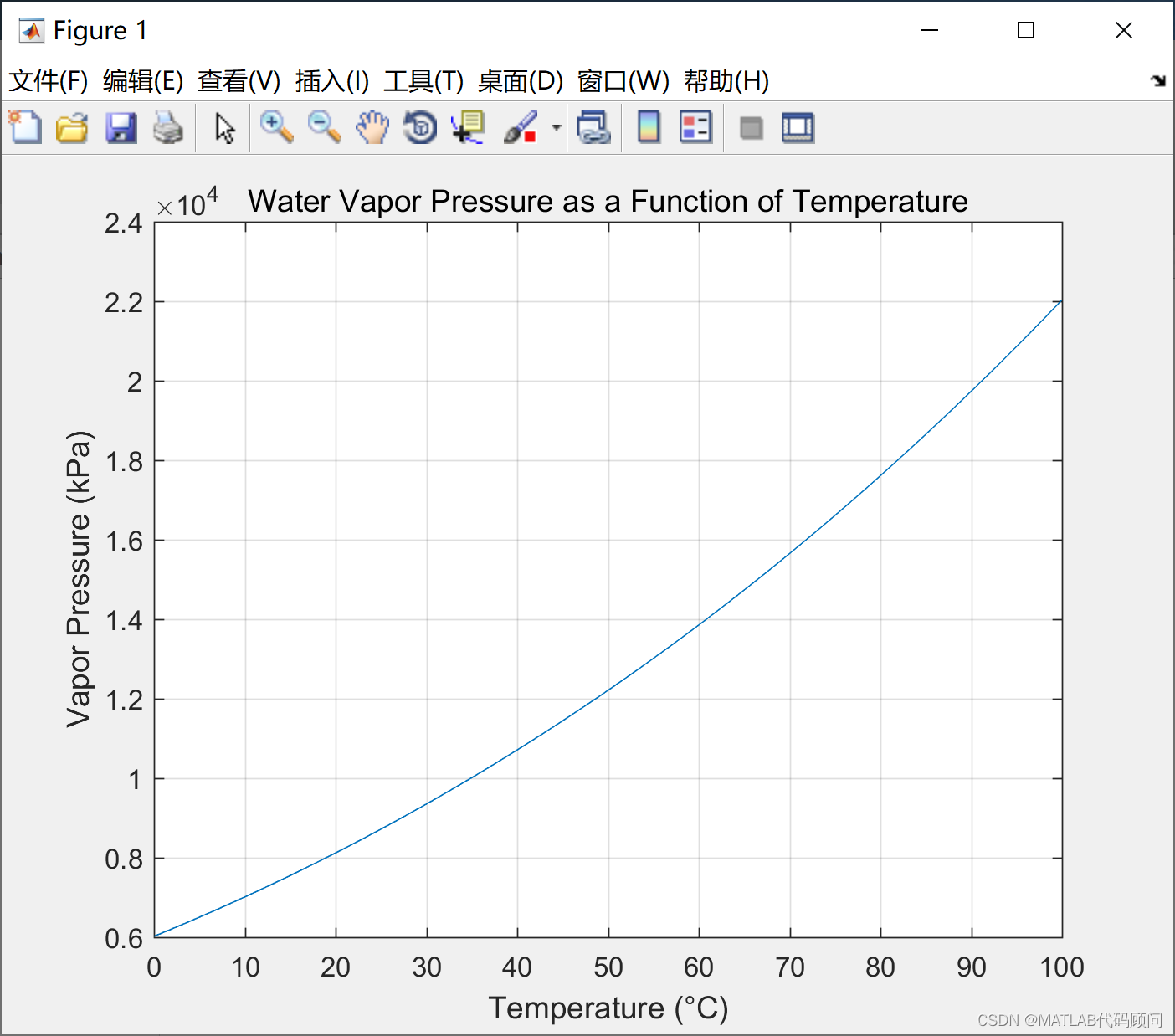
MATLAB绘制蒸汽压力和温度曲线
蒸汽压力与温度之间的具体关系公式一般采用安托因方程(Antoine Equation),用于描述纯物质的蒸汽压与温度之间的关系。安托因方程的一般形式如下: [\log_{10} P A - \frac{B}{C T}] 其中, (P) 是蒸汽压(…...
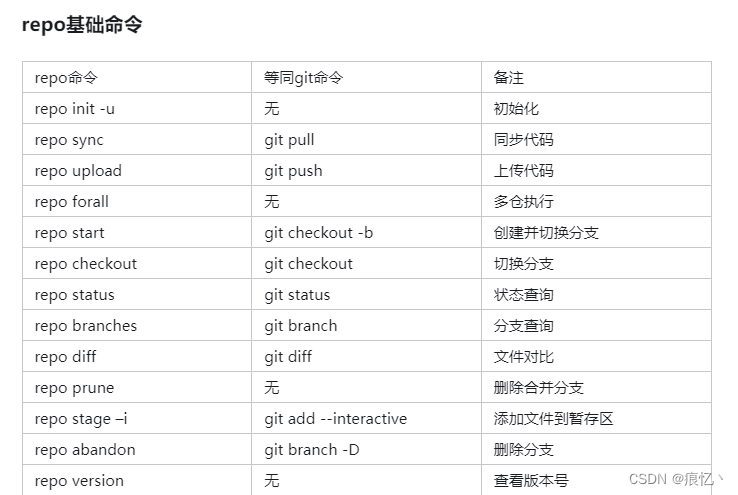
repo跟git的关系
关于repo 大都讲的太复杂了,大多是从定义角度跟命令角度去讲解,其实从现实项目使用角度而言repo很好理解. 我们都知道git是用来管理项目的,多人开发过程中git功能很好用.现在我们知道一个项目会用一个git仓库去管理,项目的开发过程中会使用git创建分支之类的来更好的维护项目代…...
Mysql 8.0 -- 最新版本安装(保姆级教程)
Mysql 8.0 -- 最新版本安装(保姆级教程) 一,下载Mysql数据库: 官网链接:https://www.mysql.com/downloads/ 二,安装Mysql: 三,找到Mysql安装目录: 找到mysql安装目录…...

sql优化思路
sql的优化经验 这里解释一下SQL语句的优化的原理 1.指明字段名称,可以尽量使用覆盖索引,避免回表查询,因此可以提高效率 2.字面意思,无需过多赘述。索引就是为了提高查询效率的。 3.图中两条sql直接可以使用union all 或者 uni…...

gin学习1-7
package mainimport ("github.com/gin-gonic/gin""net/http" )// 响应json还有其他响应差不多可以去学 func _string(c *gin.Context) {c.String(http.StatusOK, "lalal") } func _json(c *gin.Context) {//json响应结构体type UsetInfo struct …...
likeshop多商户单商户商城_likeshop跑腿源码_likeshop物品租赁系统开源版怎么配置小程序对接?
本人是商业用户所以能持续得到最新商业版,今天我说下likeshop里面怎么打包小程序,大家得到程序时候会发现它有admin目录 app目录 server目录 这三个目录分别是做什么呢? 1.admin目录 下面都是架构文件使用得是Node.js打包得,至于…...

(done) LSTM 详解 (包括它为什么能缓解梯度消失)
RNN 参考视频:https://www.bilibili.com/video/BV1e5411K7oW/?p2&spm_id_frompageDriver&vd_source7a1a0bc74158c6993c7355c5490fc600 LSTM 参考视频:https://www.bilibili.com/video/BV1qM4y1M7Nv?p5&vd_source7a1a0bc74158c6993c7355c5…...
springboot使用研究
map-underscore-to-camel-case: true 开启驼峰命名 GetMapping("/userInfo")public Result<Users> userInfo(RequestHeader(name "Authorization") String token,HttpServletResponse response) {Map<String, Object> map JwtUtil.parseT…...

老旧房屋用电线路故障引起的电气火灾预防对策
摘 要:在我国新农村建设方针指引下,农村地区的发展水平有了显著提高。在农村经济发展中,我们也要认识到其中存在的风险隐患问题,其中重要的就是火灾事故。火灾事故给农村发展带来的不利影响,不仅严重威胁到农村群众的生…...
OpenAI发布GPT-4.0使用指南
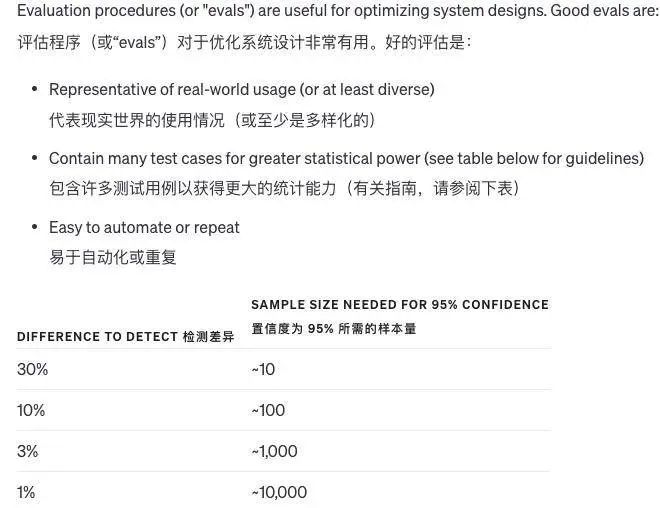
大家好,ChatGPT 自诞生以来,凭借划时代的创新,被无数人一举送上生成式 AI 的神坛。在使用时,总是期望它能准确理解我们的意图,却时常发现其回答或创作并非百分之百贴合期待。这种落差可能源于我们对于模型性能的过高期…...

【WEEK11】学习目标及总结【Spring Boot】【中文版】
学习目标: 学习SpringBoot 学习内容: 参考视频教程【狂神说Java】SpringBoot最新教程IDEA版通俗易懂员工管理系统 页面国际化登录功能展示员工列表增加员工修改员工信息删除及404处理 学习时间及产出: 第十一周MON~SAT 2024.5.6【WEEK11】…...
Unity 性能优化之图片优化(八)
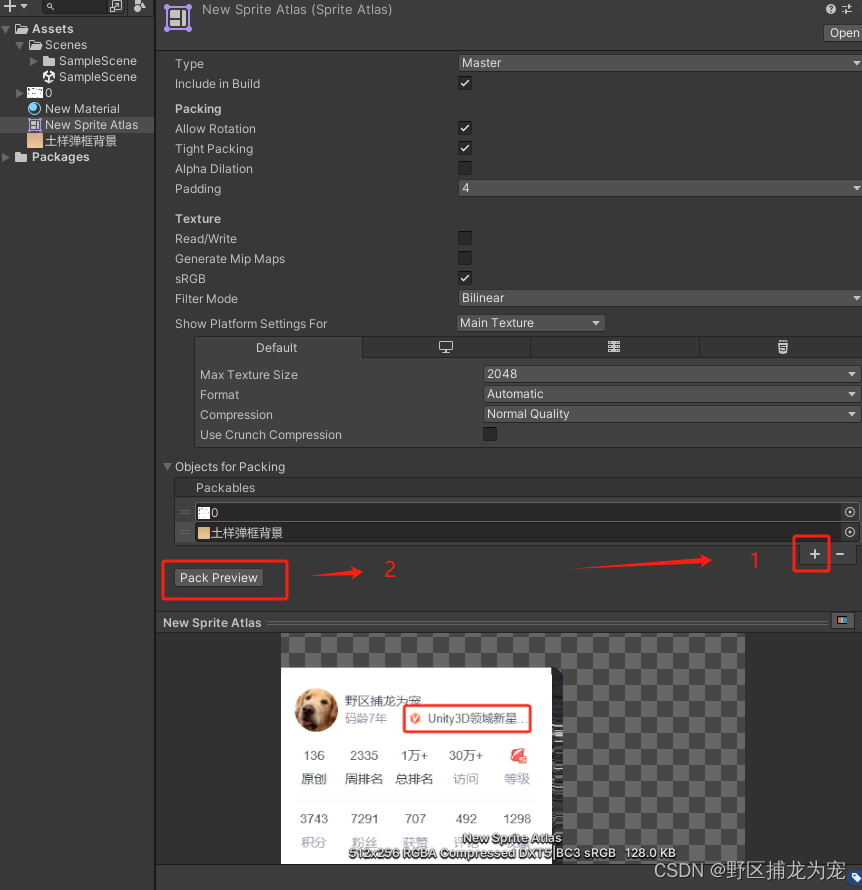
提示:仅供参考,有误之处,麻烦大佬指出,不胜感激! 文章目录 前言一、可以提前和美术商量的事1.避免内存浪费(UI图片,不是贴图)2.提升图片性能 二、图片优化1.图片Max Size修改&#x…...
C++类细节,面试题02
文章目录 2. 虚函数vs纯虚函数3. 重写vs重载vs隐藏3.1. 为什么C可以重载? 4. 类变量vs实例变量5. 类方法及其特点6. 空类vs空结构体6.1. 八个默认函数:6.2. 为什么空类占用1字节 7. const作用7.1 指针常量vs常量指针vs常量指针常量 8. 接口vs抽象类9. 浅…...

Stylus的引入
Stylus是一个CSS预处理器,它允许开发者使用更高级的语法来编写CSS,并提供了一些额外的功能来简化和增强CSS的编写过程。以下是关于Stylus的详解和引入方法的详细介绍: 一、Stylus的详解 特点和功能: 变量:允许你定义…...
前端框架-echarts
Echarts 项目中要使用到echarts框架,从零开始在csdn上记笔记。 这是一个基础的代码,小白入门看一下 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" co…...
【StarRocks系列】 Trino 方言支持
我们在之前的文章中,介绍了 Doris 官方提供的两种方言转换工具,分别是 sql convertor 和方言 plugin。StarRocks 目前同样也提供了类似的方言转换功能。本文我们就一起来看一下这个功能的实现与 Doris 相比有何不同。 一、Trino 方言验证 我们可以通过…...
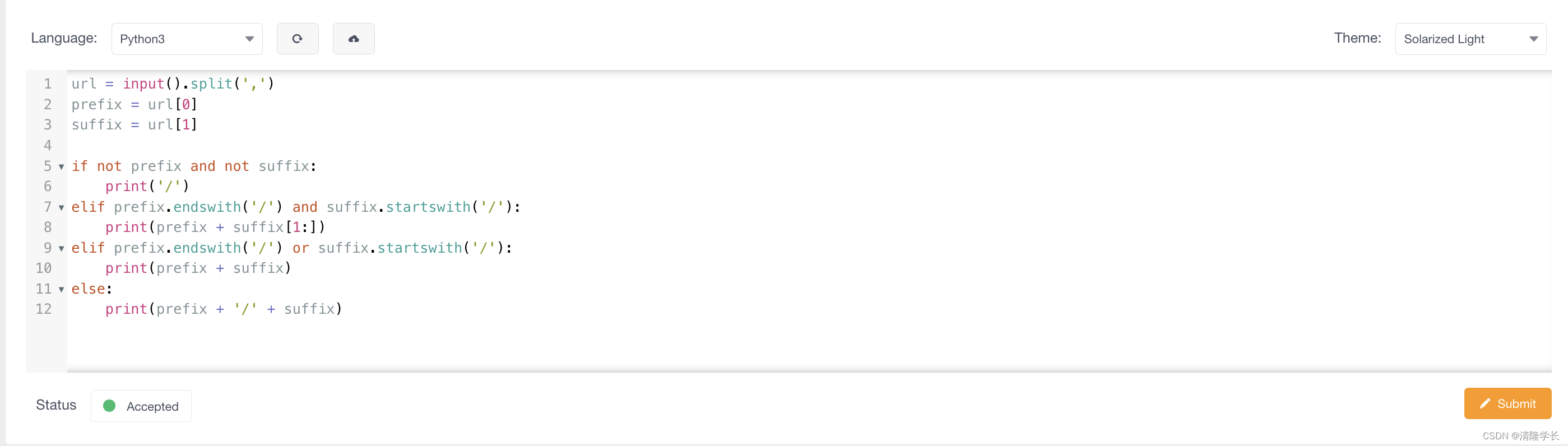
【2024最新华为OD-C卷试题汇总】URL拼接 (100分) - 三语言AC题解(Python/Java/Cpp)
🍭 大家好这里是清隆学长 ,一枚热爱算法的程序员 ✨ 本系列打算持续跟新华为OD-C卷的三语言AC题解 💻 ACM银牌🥈| 多次AK大厂笔试 | 编程一对一辅导 👏 感谢大家的订阅➕ 和 喜欢💗 文章目录 前…...

【ARM 嵌入式 C 字符串系列 23.7 -- C 实现函数 isdigit 和 isxdigit】
请阅读【嵌入式开发学习必备专栏 】 文章目录 isdigit 和 isxdigit C代码实现实现 isdigit实现 isxdigit使用示例 isdigit 和 isxdigit C代码实现 在C语言中,isdigit和isxdigit函数用于检查一个字符是否分别为十进制数字或十六进制数字。以下是这两个函数的简单实现…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

解决Ubuntu22.04 VMware失败的问题 ubuntu入门之二十八
现象1 打开VMware失败 Ubuntu升级之后打开VMware上报需要安装vmmon和vmnet,点击确认后如下提示 最终上报fail 解决方法 内核升级导致,需要在新内核下重新下载编译安装 查看版本 $ vmware -v VMware Workstation 17.5.1 build-23298084$ lsb_release…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

GitFlow 工作模式(详解)
今天再学项目的过程中遇到使用gitflow模式管理代码,因此进行学习并且发布关于gitflow的一些思考 Git与GitFlow模式 我们在写代码的时候通常会进行网上保存,无论是github还是gittee,都是一种基于git去保存代码的形式,这样保存代码…...
