【算法作业】均分卡牌,购买股票
问题描述
-
John 有两个孩子,在 John病逝后,留下了一组价值不一定相同的魔卡, 现在要求你设计一种策略,帮John的经管人将John的这些遗产分给他的两个孩子,使得他们获得的遗产差异最小(每张魔卡不能分拆)。
-
假设已知某股票连续若干天的股价,并且如何时候你手上只能由一支股票,即如果你要买入就得先将手上股票卖出,设计一个算法来计算你所能获取的最大利润。你最多可以完成 k笔交易。也就是说,你最多可以买k 次,卖 k 次。
输入:k = 2, prices = [3,2,7,5,1,4] 输出:87-2 + 4-1
解题思路
T1
这是一个经典的贪心算法问题:
- 将所有的魔卡按照价值从大到小排序。
- 从价值最高的魔卡开始,依次分配给两个孩子中当前遗产较少的那个孩子。
- 重复步骤2直到所有的魔卡都被分配完毕。
这种贪心分东西的思路非常常见,一眼望穿
类似的题目还有捡大小垃圾放两个垃圾袋呀等等。
T2
那么这道题到底是贪心还是动规呢?
我们知道动规有一道经典例题,就是非升子序列,不觉得这题有几分相似,都是必须从前往后求最优。其实要证明贪心算法不行只要举个反例就行了。
于是就根据经验按照动规的思路来思考。考虑使用二维数组dp[i][j],代表当前状态的最大利润,i代表当前是第i次买卖,j代表当前是第j天。
对于每个状态都有买和不买。为什么是买和不买呢,不是还有卖吗?其实是赚钱和不赚钱这两种选择,赚钱是卖与买之间的差值。所以这道题比一般的动态规划要更复杂些。
对于每一次买卖,必须有买才有卖,先用maxDiff包括因为买股票亏的钱,一开始由于没有股票,就等于-prices[1]。这个亏的钱也完全不是负数亏的钱,还要包括之前(上一次买卖)因为赚钱累计的成本,这个maxDiff就是代表本次买卖状态下的累计成本(比较难理解)。所以 m a x D i f f = m a x ( m a x D i f f , d p [ i − 1 ] [ j ] − p r i c e s [ j ] ) maxDiff = max(maxDiff, dp[i-1][j] - prices[j]) maxDiff=max(maxDiff,dp[i−1][j]−prices[j])
对于每一天,都有去赚钱和不赚钱。不赚钱利润等于昨天的利润,去赚钱的利润等于累计成本maxDiff加上prices[j],因此 d p [ i ] [ j ] = m a x ( d p [ i ] [ j − 1 ] , p r i c e s [ j ] + m a x D i f f ) dp[i][j] = max(dp[i][j-1], prices[j] + maxDiff) dp[i][j]=max(dp[i][j−1],prices[j]+maxDiff)
在样例下,dp运算结果如下所示。
| prices | 3 | 2 | 7 | 5 | 1 | 4 |
|---|---|---|---|---|---|---|
| dp[1][j] | 0 | 0 | 5 | 5 | 5 | 5 |
| dp[2][j] | 0 | 0 | 5 | 5 | 5 | 8 |
这个dp[k][n]就是answer。
完整代码
T1
#include <iostream>
#include <algorithm>using namespace std;// 分配遗产的函数
void distributeInheritance(int cards[], int n) {// 排序魔卡sort(cards, cards + n, greater<int>());// 初始化两个孩子的遗产值int child1_inheritance = 0;int child2_inheritance = 0;// 分配遗产for (int i = 0; i < n; ++i) {if (child1_inheritance <= child2_inheritance) {child1_inheritance += cards[i];} else {child2_inheritance += cards[i];}}// 输出两个孩子的遗产差异cout << "遗产差异最小为:" << abs(child1_inheritance - child2_inheritance) << endl;
}int main() {// 输入魔卡数量int n;cout << "请输入魔卡数量:";cin >> n;// 输入每张魔卡的价值int cards[n];cout << "请输入每张魔卡的价值:" << endl;for (int i = 0; i < n; ++i) {cin >> cards[i];}// 调用分配遗产函数distributeInheritance(cards, n);return 0;
}/* sample input
8
2 5 6 7 1 7 4 3
*/
输出结果
请输入魔卡数量:8
请输入每张魔卡的价值:
2 5 6 7 1 7 4 3
遗产差异最小为:1
T2
#include<bits/stdc++.h>
using namespace std;
int main(){int n,k,prices[100],dp[101][101]; // 动态规划数组大小修改为dp[101][101]cin>>n>>k;memset(dp,0,sizeof(dp));memset(prices,0,sizeof(prices));for(int i=1;i<=n;i++)cin>>prices[i];for(int i=1;i<=k;i++){int maxDiff = -prices[1]; // 数组prices的下标从1开始for(int j=1;j<=n;j++){ dp[i][j] = max(dp[i][j-1],prices[j] + maxDiff);maxDiff = max(maxDiff, dp[i-1][j] - prices[j]);}}cout<<dp[k][n]<<endl;// 打印dp数组cout<<"|dp|";for(int i=1;i<=n;i++)cout<<i<<"|";cout<<endl;cout<<"|";for(int i=1;i<=n+1;i++)cout<<"-|";cout<<endl;for(int i=1;i<=k;i++){cout<<"|"<<i<<"|";for(int j=1;j<=n;j++)cout<<dp[i][j]<<"|";cout<<"\n";}return 0;
}/* simple input
6 2
3 2 7 5 1 4
*/
输出结果
6 2
3 2 7 5 1 4
8
|dp|1|2|3|4|5|6|
|-|-|-|-|-|-|-|
|1|0|0|5|5|5|5|
|2|0|0|5|5|5|8|
相关文章:

【算法作业】均分卡牌,购买股票
问题描述 John 有两个孩子,在 John病逝后,留下了一组价值不一定相同的魔卡, 现在要求你设计一种策略,帮John的经管人将John的这些遗产分给他的两个孩子,使得他们获得的遗产差异最小(每张魔卡不能分拆&#…...
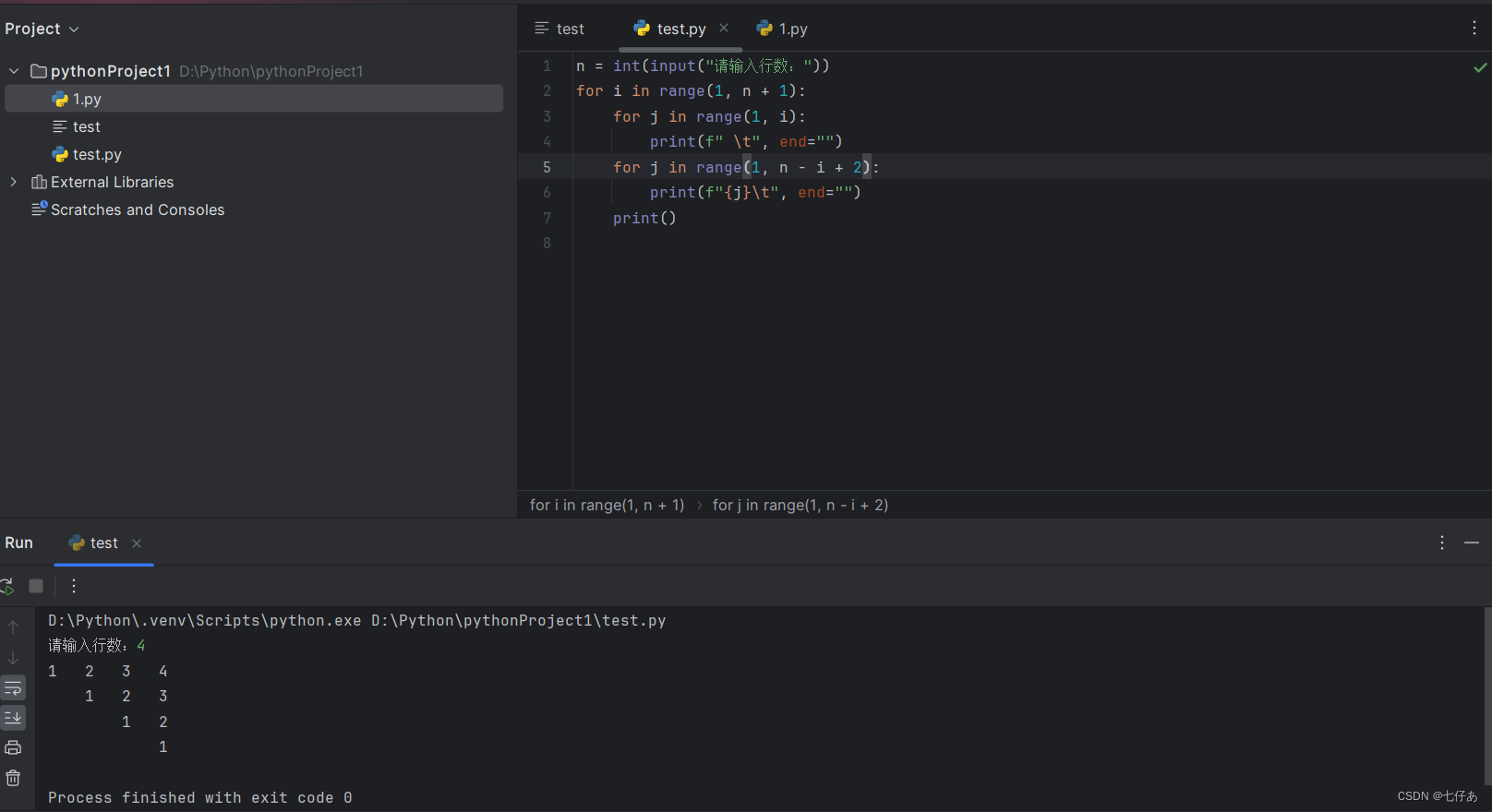
python作业
题目 分析 步骤: 判断先画空格还是数字 当有n层时,第i层有多少个空格第i层的起始数字是几,结尾是几,即数字取值范围当有n层时,第i层有多少个数字 代码 模式A n int(input("请输入行数:")) for i in range(…...

【Linux的文件篇章 - 管道文件】
Linux学习笔记---013 Linux的管道文件1、进程间通信1.1、进程为什么要通信?1.2、进程如何通信?1.3、进程通信的方式? 2、匿名管道2.1、理解一种现象2.2、基本概念和管道原理 3、管道的使用3.1、代码样例3.2、如何使用管道通信呢?3…...

C# 局部静态函数,封闭方法中的最佳选择
C# 局部静态函数,封闭方法中的最佳选择 简介特性 应用场景辅助计算递归与尾递归优化筛选与过滤操作查找与映射操作 生命周期静态局部函数 vs 普通局部函数性能封装性可读性 简介 C# 局部静态函数(Local Static Functions)是一种函数作用域内…...
安装)
【MySQL】MySQL 8.4.0 长期支持版(LTS)安装
就在2024年 “5.1” 节前,MySQL官方发布了8.4.0长期支持版(LTS - Long Term Support)。根据官方提供的文档,在本地虚拟机进行安装测试。 安装、配置和启动过程记录如下: 第一步,上传到安装包(my…...

nest中的ORM
在 Nest.js 中执行 SQL 查询通常涉及使用 TypeORM 或 Sequelize 这样的 ORM(对象-关系映射)库。这些库使得在 Nest.js 应用程序中连接和操作 SQL 数据库变得更加简单和直观。 以下是一个使用 TypeORM 在 Nest.js 中执行 SQL 查询的示例代码:…...
如何保证数据的完整性?)
TCP(Transmission Control Protocol,传输控制协议)如何保证数据的完整性?
TCP(Transmission Control Protocol,传输控制协议)通过一系列机制来保证数据传输的可靠性和无错性,这些机制主要包括: 校验和:TCP报文段包含一个校验和字段,用于检测数据在传输过程中是否出错。…...

Numpy库介绍
NumPy(Numerical Python的缩写)是Python中用于科学计算的一个强大的库。它提供了高性能的多维数组对象(即ndarray)、用于处理这些数组的工具以及用于数学函数操作的函数。让我为你介绍一下它的一些主要功能: 1. 多维数…...
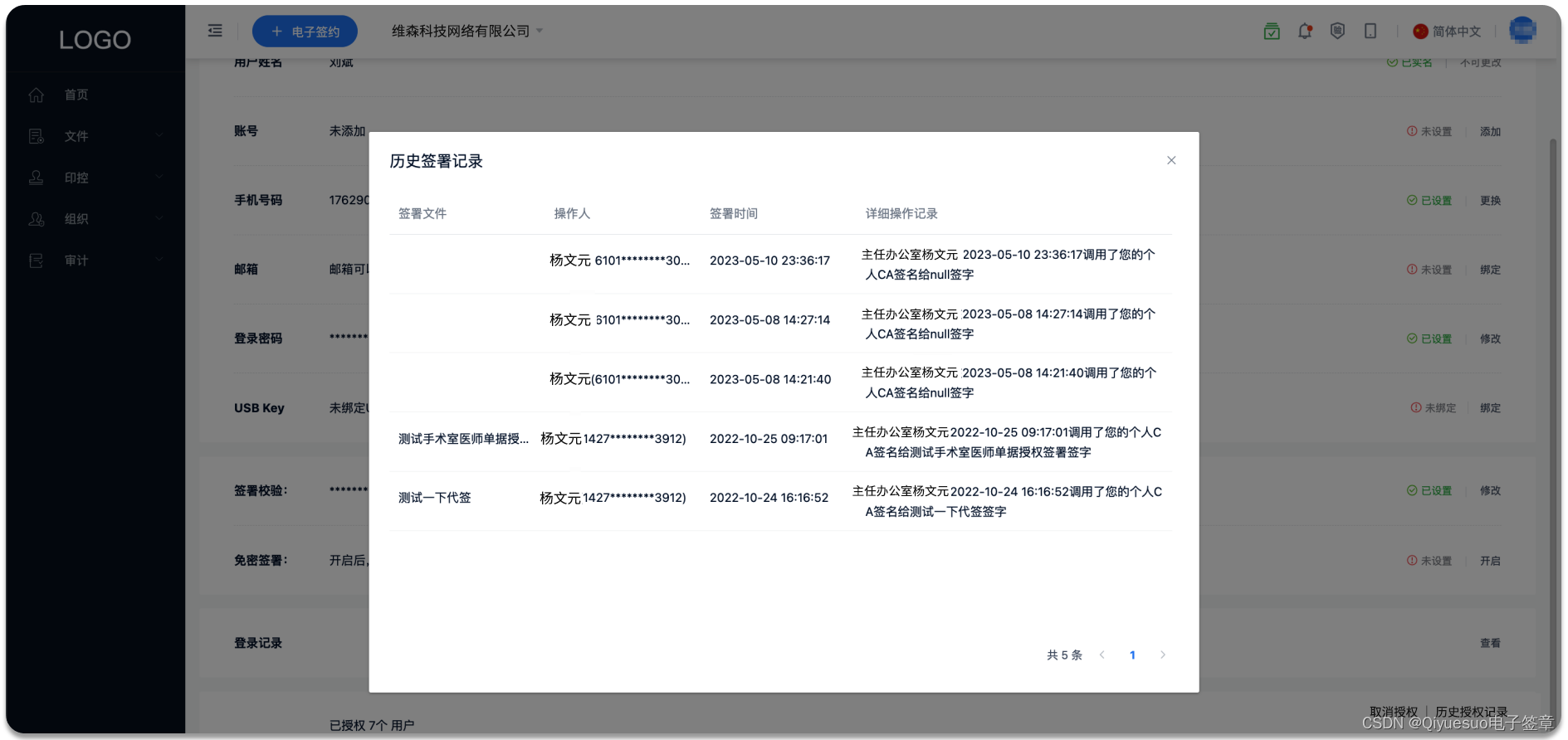
临时有事无法及时签字盖章?试试用契约锁设置“代理人”
遇到“领导休假中、在开重要会议、外出考察或者主任医生手术中等”一段时间内不方便或者无法及时签字盖章的情况怎么办?业务推进不了只能干等? 契约锁电子签及印控平台支持印章、签名“临时授权”、“代理签署”,实现指定人、指定时间段、指定…...

数据库权限管理
1.查看系统级权限(global level) Select * from mysql.user\G; 2.查看数据库中所有表的权限 Select * from mysql.db\G 3.远程连接数据库 第一步在有数据库服务上的主机上:授权 grant all on *.* to root192.168.40.83 identified by Zxy20234; 第…...

如何创建一个 Django 应用并连接到数据库
简介 Django 是一个用 Python 编写的免费开源的 Web 框架。这个工具支持可扩展性、可重用性和快速开发。 在本教程中,您将学习如何为一个博客网站建立与 MySQL 数据库的初始基础。这将涉及使用 django-admin 创建博客 Web 应用程序的骨架结构,创建 MyS…...

【算法刷题day44】Leetcode:518. 零钱兑换 II、377. 组合总和 Ⅳ
文章目录 Leetcode 518. 零钱兑换 II解题思路代码总结 Leetcode 377. 组合总和 Ⅳ解题思路代码总结 草稿图网站 java的Deque Leetcode 518. 零钱兑换 II 题目:518. 零钱兑换 II 解析:代码随想录解析 解题思路 先遍历物品,再遍历背包。 代码…...
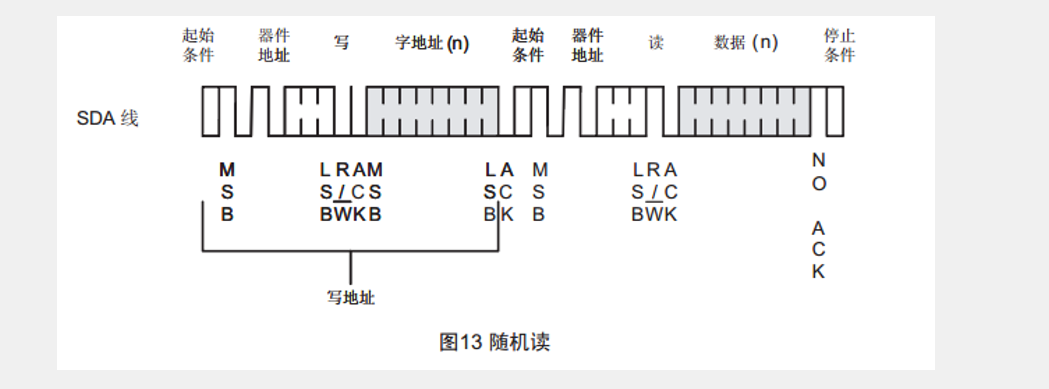
『51单片机』AT24C02[IIC总线]
存储器的介绍 ⒈ROM的功能⇢ROM的数据在程序运行的时候是不容改变的,除非你再次烧写程序,他就会改变,就像我们的书本,印上去就改不了了,除非再次印刷,这个就是ROM的原理。 注→在后面发展的ROM是可以可写可…...

Jenkins与Rancher的配合使用
Jenkins和Rancher是两个常用的DevOps工具,可以很好地配合使用来实现持续集成和持续部署。 Jenkins是一个开源的自动化构建工具,可以实现自动化的代码构建、测试和部署等一系列操作。可以通过Jenkins来触发构建任务,例如从代码仓库中拉取最新的…...

GIS入门,常用的多边形平滑曲线算法介绍和JavaScript的多边形平滑曲线算法库chaikin-smooth的实现原理和使用
前言 本章介绍一下常用的多边形平滑曲线算法及其使用案例。 多边形平滑算法通常用于图形处理或计算机图形学中,以使线条或曲线在连接处平滑过渡,而不出现明显的棱角或断裂。多边形平滑算法有多种实现方法,其中一些常见的有下面几种: 贝塞尔曲线插值(Bezier Curve Interpo…...

气膜体育馆内部的采光效果如何?—轻空间
气膜体育馆内部的采光效果如何?这是许多人对这种创新建筑的一个关键关注点。 首先,气膜体育馆的采光性非常好。阳光透过屋顶时以漫射光的方式进入室内,这种透射方式使得室内的光线柔和而均匀。从内部观察,整个屋顶就像一个连续的明…...
)
矩阵的对称正定性判决(复习)
文章目录 本科学的数学知识忘的太快了 如何判断一个实矩阵是否是对称正定 在线性代数中,一个实对称矩阵是否为正定可以通过以下方法判断: 对称性: 首先,确认矩阵是否对称,即矩阵的转置是否等于其本身。 特征值检查&…...
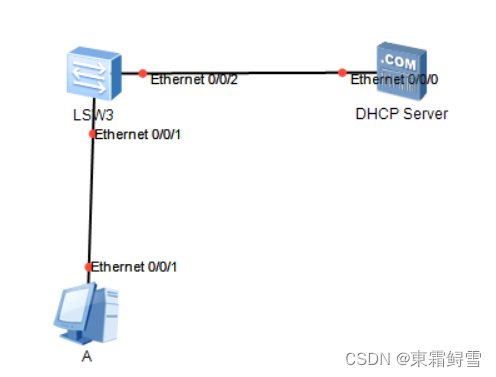
网络安全之DHCP详解
DHCP:Dynamic Host Configration Protocol 动态主机配置协议 某一协议的数据是基于UDP封装的,当它想确保自己的可靠性时,这个协议要么选确认重传机制,要么选周期性传输。 DHCP是确认重传,【UDP|DHCP】,当DHCP分配完地…...
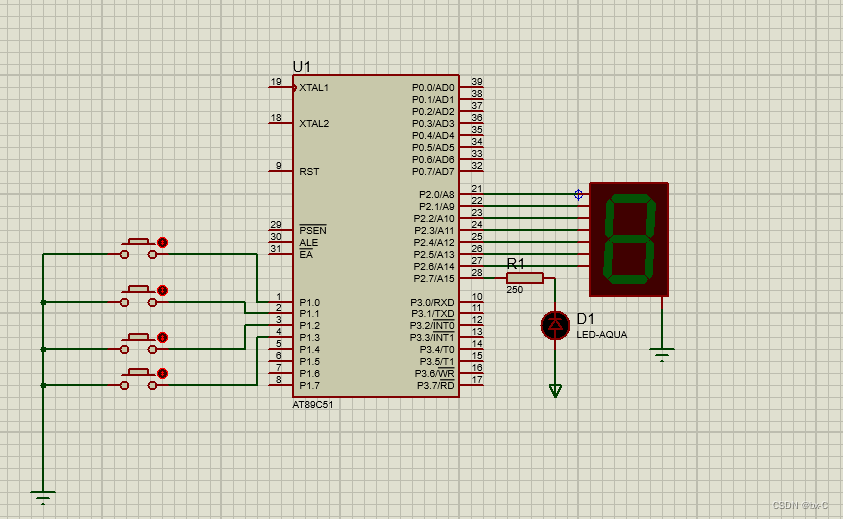
【Proteus】LED呼吸灯 直流电机调速
1.LED呼吸灯 #include <REGX51.H> sbit LEDP2^0; void delay(unsigned int t) {while(t--); } void main() {unsigned char time,i;while(1){for(time0;time<100;time){for(i0;i<20;i){LED0;delay(time);LED1;delay(100-time);}}for(time100;time>0;time--){fo…...
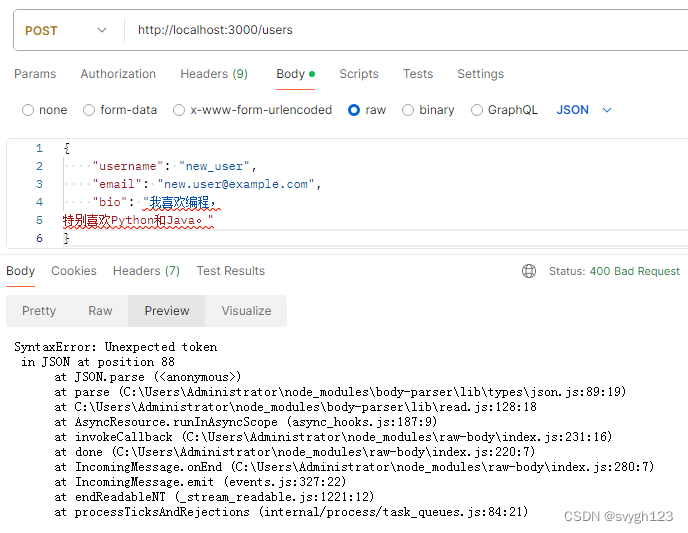
今天遇到一个GPT解决不了的问题
问题描述 你好,postman的一个post请求,编辑器里面放了一个很长的json数据,报Tokenization is skipped for long lines for performance reasons. This can be configured via editor.maxTokenizationLineLength.,但是同样的数据&a…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

python打卡day49
知识点回顾: 通道注意力模块复习空间注意力模块CBAM的定义 作业:尝试对今天的模型检查参数数目,并用tensorboard查看训练过程 import torch import torch.nn as nn# 定义通道注意力 class ChannelAttention(nn.Module):def __init__(self,…...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院挂号小程序
一、开发准备 环境搭建: 安装DevEco Studio 3.0或更高版本配置HarmonyOS SDK申请开发者账号 项目创建: File > New > Create Project > Application (选择"Empty Ability") 二、核心功能实现 1. 医院科室展示 /…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...
