2023 广东省大学生程序设计竞赛(部分题解)
目录
A - Programming Contest
B - Base Station Construction
C - Trading
D - New Houses
E - New but Nostalgic Problem
I - Path Planning
K - Peg Solitaire
A - Programming Contest
签到题:直接模拟
直接按照题目意思模拟即可,为了好去重,我们使用set即可
void solve(){int l,r; cin>>l>>n;set<int> s;while(n--){int x; cin>>x;s.insert(x);}cin>>r;int ans = 0;for(int i=l;i<=r;i++) ans += !s.count(i);cout << ans << endl;return ;
}
B - Base Station Construction
银牌题:优先队列优化dp
我们可以读懂题目也就是说对于一个区间[l,r]而言我们一定要选一个,可以知道r+1从l转移过来肯定是最优的,由此我们可以对于每一个点维护最优的前一个点的转移,同时注意到后缀一定是满足前缀的要求的所以pre[r+1]=max(pre[r+1],l)同时再用前缀最大值处理一下,我们定义在第i个点建立电站同时满足前面的每一个区间的同时的最优解为,转移方程为
,为前缀的点同时随着i的增大j一定是同时增大的变化,所以可以考虑使用优先队列维护dp即可,同时注意怎么判断最后答案是上面,我们可以++n这样满足答案就是
void solve(){cin>>n;vector<int> a(n+5),pre(n+5),q(n+5);vector<LL> dp(n+5);for(int i=1;i<=n;i++) cin>>a[i];n++;cin>>m;while(m--){int l,r; cin>>l>>r;pre[r+1]=max(pre[r+1],l);}for(int i=1;i<=n;i++) pre[i]=max(pre[i-1],pre[i]);int hh=0,tt=0;q[0]=0;for(int i=1;i<=n;i++){while(hh<=tt and q[hh]<pre[i]) hh++;dp[i] = dp[q[hh]] + a[i];while(hh<=tt and dp[q[tt]]>=dp[i]) tt--; q[++tt]=i;}cout << dp[n] << endl;return ;
}C - Trading
签到题:贪心
我们可以有个明显的结论就是从价格最便宜的买入,在贵的卖出就行了,进一步贪心我肯定是买最多的同时卖了最优,所以就是买一半卖一半即可
void solve(){cin>>n;LL sum = 0;for(int i=1;i<=n;i++){int a,b; cin>>a>>b;w[i]={a,b};sum += b;}sort(w+1,w+1+n);LL buy = 0,cnt = 0;for(int i=1;i<=n;i++){auto [a,b]=w[i];int now = min(sum/2-cnt,b);buy += (LL)a*now;cnt += now;}LL use = 0,num = 0;for(int i=n;i>=1;i--){auto [a,b]=w[i];int now = min(sum/2-num,b);use += (LL)a*now;num += now;}LL ans = use - buy;cout << ans << endl;return ;
}D - New Houses
签到题:贪心
设有邻居贡献为x,无为y
我们有个明显的结论就是如果你是有邻居优就让你有邻居,否则让你没邻居,我们一开始可以所有人挤在一起,放置在前i个位置,,(特判n==1)接着按照没有邻居贡献大的来排序,可以注意到多了几个位置就可以有多少人是可以没有邻居的同时贡献要大于有邻居的时候才考虑,贡献为y-x,同时注意到如果说后面排了n-1个人的时候前面最开始就没有邻居了,就需要特判到底是合在一起还是分开贡献最优即可
void solve(){cin>>n>>m;LL ans = 0;// 一开始所有人都挤在一起for(int i=1;i<=n;i++){int x,y; cin>>x>>y;a[i]={x,y};ans += x;}if(n==1){cout << a[1].second << endl;return ;}sort(a+1,a+1+n,[](PII a,PII b){return a.second-a.first>b.second-b.first;});int pos = 0;for(int i=1;i<=m-n and a[i].second-a[i].first>=0 and i<=n;i++){auto [x,y]=a[i];ans += y-x;pos = i;}if(pos==n-1){// 由于前面挤在一起的只有一个人 考虑合在一起或者是分开ans = max(ans+a[n-1].first-a[n-1].second,ans-a[n].first+a[n].second);}cout << ans << endl;return ;
}E - New but Nostalgic Problem
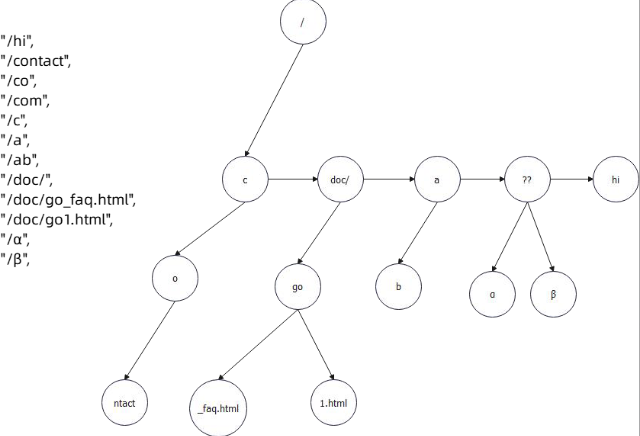
银牌-金牌题:trie树+dfs贪心
我们选出m个使得结果最小我们可以发现要维护的是最长公共前缀,那么我们考虑字符的存储可以考虑使用trie树,我们有一个贪心的想法,我一定是从aaa...abc....这样的结果来看是不是满足数量最优的,如果说对于当前已经选了“abc"下一个是选择d组合为abcd,那么满足是abcd的前缀起码要选择两个,同时前面的abc[a-c]肯定是都得加上因为如果这前面有更优解肯定跑到前面去了,同时对于[e-z]每一个分支最多选择一个,因为如果选择多了当前结果就不是abcd了,同时我们可以发现这样也就是遍历了每一个字符串而已,所以时间是符合要求,接下来就是用实现即可
int tr[N][26],sum[N],ed[N];
string s,ans;
bool ok;
void insert(){int p = 0;for(auto&v:s){int x=v-'a';if(!tr[p][x]) tr[p][x]=++idx;p = tr[p][x];sum[p]++;}ed[p]++;
}
void used(){for(int i=0;i<=idx;i++){for(int j=0;j<26;j++) tr[i][j]=0;sum[i]=ed[i]=0;}ok = false;idx = 0;ans.clear();
}
void dfs(int u,int last){if(ok) return ;int s = 0;//ab 之后 aba abb abc abd ...//得到的答案是abint now = last + ed[u];for(auto v : tr[u]) s += min(1,v); // 表示对于当前分支接着都取不一样if(now + s>=m){cout << (u ? ans : "EMPTY") << endl;ok = true;return ;}int pre = 0;for(int i=0;i<26;i++){if(!tr[u][i]) continue;// 表示需要加一个分支去走ans.push_back(i+'a');dfs(tr[u][i],now+pre+s-1); // 表示在s取过了ans.pop_back();pre += sum[tr[u][i]]-1; // 表示这个字母在s取过了}
}
void solve(){cin>>n>>m;for(int i=1;i<=n;i++){cin>>s;insert();}dfs(0,0);used();return ;
}
F - Traveling in Cells
金牌题:二分+动态开点线段树+树装数组
我们有个明显的想法就是对于操作3二分找到最远左右边界即可,但是对于左右边界如果判断是不是符合集合的值难以解决,我们可以注意到 颜色的数量过多,同时还得支持颜色的修改,我们考虑使用动态开点线段树来维护,对于每一个点开出的线段树的用到的节点数量只有(n+m)logn个,我们使用这个数据结构可以维护要求,同时对于查询左右区间的贡献已经修改值都可以通过树装数组来维护,核心还是考察了动态开点线段树
int t,n,m,k,idx;
struct code{int l,r;int val;
}tr[N*40];int c[N],v[N],s[M];
int rc[N];
LL vc[N];void update(int p){tr[p].val = tr[tr[p].l].val + tr[tr[p].r].val;
}void change(int &p,int l,int r,int x,int val){if(!p) p = ++ idx;if(l==r){tr[p].val+=val;return ;}int mid = l+r>>1;if(x<=mid) change(tr[p].l,l,mid,x,val);else change(tr[p].r,mid+1,r,x,val);update(p);
}int query(int p,int l,int r,int L,int R){if(!p) return 0;if(L <= l and r <= R) return tr[p].val;int mid = l+r>>1;int res = 0;if(L<=mid) res += query(tr[p].l,l,mid,L,R);if(R>mid) res += query(tr[p].r,mid+1,r,L,R);return res;
}
void add(int k,int x){for(int i=k;i<=n;i+=lowbit(i)) vc[i] += x;
}
LL ask(int k){LL res = 0;for(int i=k;i;i-=lowbit(i)) res += vc[i];return res;
}
bool check(int l,int r){int cnt = 0;for(int i=1;i<=k;i++)cnt += query(rc[s[i]],1,n,l,r);return cnt == r-l+1;
}
void clear(){for(int i=1;i<=n;i++) rc[i]=vc[i]=0;for(int i=1;i<=idx;i++) tr[i].l=tr[i].r=tr[i].val=0;idx = 0;
}
void solve(){clear();cin>>n>>m;for(int i=1;i<=n;i++){cin>>c[i];change(rc[c[i]],1,n,i,1);}for(int i=1;i<=n;i++){cin>>v[i];add(i,v[i]);}while(m--){int op,p,x;cin>>op;if(op==1){cin>>p>>x;change(rc[c[p]],1,n,p,-1);change(rc[x],1,n,p,1);c[p]=x;}else if(op==2){cin>>p>>x;add(p,x-v[p]);v[p]=x;}else{int pos;cin>>pos>>k;for(int i=1;i<=k;i++) cin>>s[i];LL ans = 0;int posl = pos,posr = pos;int l = 1, r = pos;while(l<r){int mid = l+r>>1;if(check(mid,pos)) r=mid;else l=mid+1; }posl = l;l = pos,r = n;while(l<r){int mid=l+r+1>>1;if(check(pos,mid)) l=mid;else r=mid-1;}posr = r;cout << ask(posr)-ask(posl-1) << endl;}}return ;
}
I - Path Planning
铜牌题:mex + 二分
我们可以注意到题目要求路径上的mex最大,如果x是可以的那么[1-x]一定是可以的,同时如果x不可以那么[x,..]一定是不可以的,所以具有二分性质,现在核心就是二分,我们可以发现路径一定是右下的走法,也就是满足要求的j一定不会比上面满足要求的j要小否则就是往回走了,由此我们可以得到二分的写法
void solve(){cin>>n>>m;vector<vector<int>> s(n+5,vector<int>(m+5));for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)cin>>s[i][j];auto check = [&](int x){int last = 0;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++)if(s[i][j]<x){if(j<last) return false;last = max(last,j);}return true;};int l=1,r=n*m;while(l<r){int mid=l+r+1>>1;if(check(mid)) l=mid;else r=mid-1;}cout << l << endl;return ;
}K - Peg Solitaire
签到-铜牌题:dfs暴力
可以注意到数据范围是很小的所以我们可以考虑直接暴力因为分支很少dfs的不会很多
按照题目意思模拟暴力即可
int ans;
int dx[]={-1,1,0,0},dy[]={0,0,1,-1};
void dfs(int cnt){ans = min(ans,cnt);if(ans==1) return ;for(int i=1;i<=n;i++)for(int j=1;j<=m;j++){if(s[i][j]){for(int u=0;u<4;u++){int a=i+dx[u],b=j+dy[u];int na=i+2*dx[u],nb=j+2*dy[u];if(1<=na and na<=n and 1<=nb and nb<=mand s[a][b] and !s[na][nb]){s[a][b]=s[i][j]=false;s[na][nb]=true;dfs(cnt-1);s[a][b]=s[i][j]=true;s[na][nb]=false;}}}}
}
void solve(){cin>>n>>m>>k;ans = k;memset(s,0,sizeof s);for(int i=1;i<=k;i++){int x,y; cin>>x>>y;s[x][y]=true;}dfs(k);cout << ans << endl;return ;
}相关文章:
2023 广东省大学生程序设计竞赛(部分题解)
目录 A - Programming Contest B - Base Station Construction C - Trading D - New Houses E - New but Nostalgic Problem I - Path Planning K - Peg Solitaire A - Programming Contest 签到题:直接模拟 直接按照题目意思模拟即可,为了好去…...
ROS2学习——Docker环境下安装于使用(1)
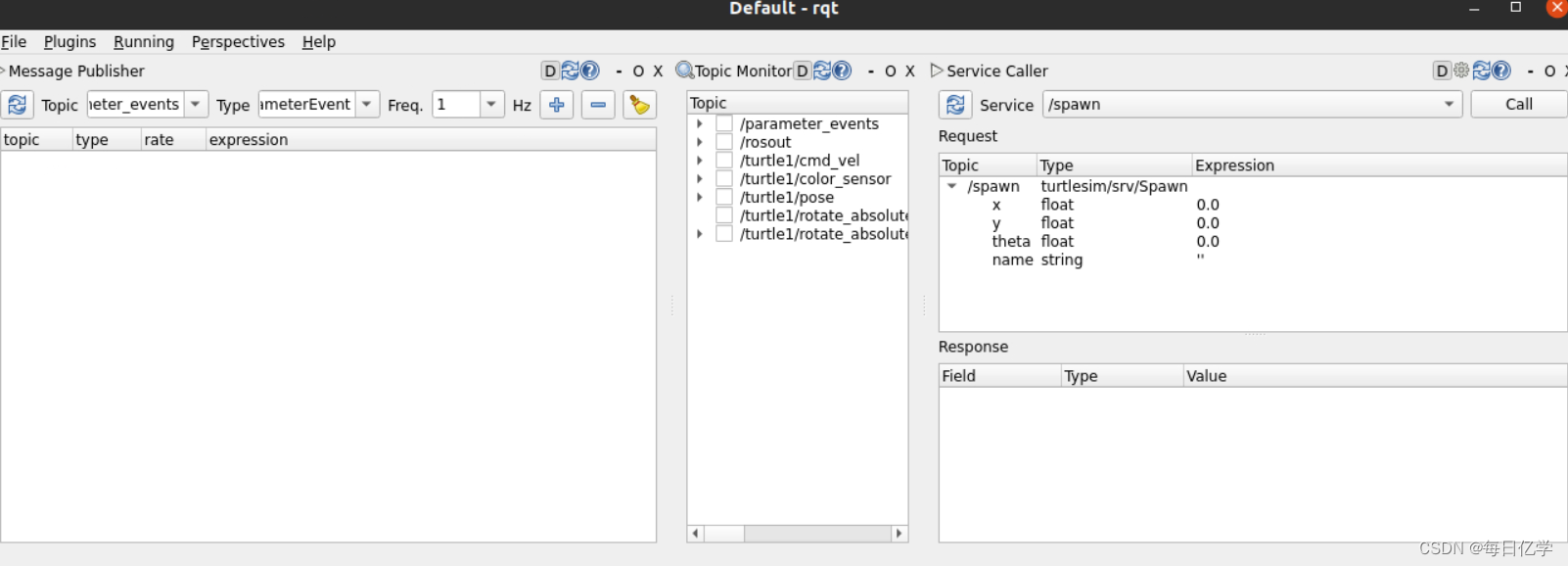
目录 一、简要 二、ROS2和ROS1区别 三、环境搭建与安装 (2)拉取ubuntu22.04镜像 (2)安装ROS2 1. 基本设置 2.设置源 3.安装ROS2功能包 4.测试 四、相关指令学习 1.小海龟测试 2.ros2 node等指令 3.rqt 一、简要 随着R…...

数据仓库之Hologres
官方文档 简介 Hologres是阿里云推出的一种云原生的实时分析型数据仓库。它是基于开源项目Apache Hudi(Hadoop Upserts Deletes and Incrementals)进行扩展和优化的。Hologres提供了高性Hologres是阿里云推出的一种云原生的实时分析型数据仓库。它是基…...
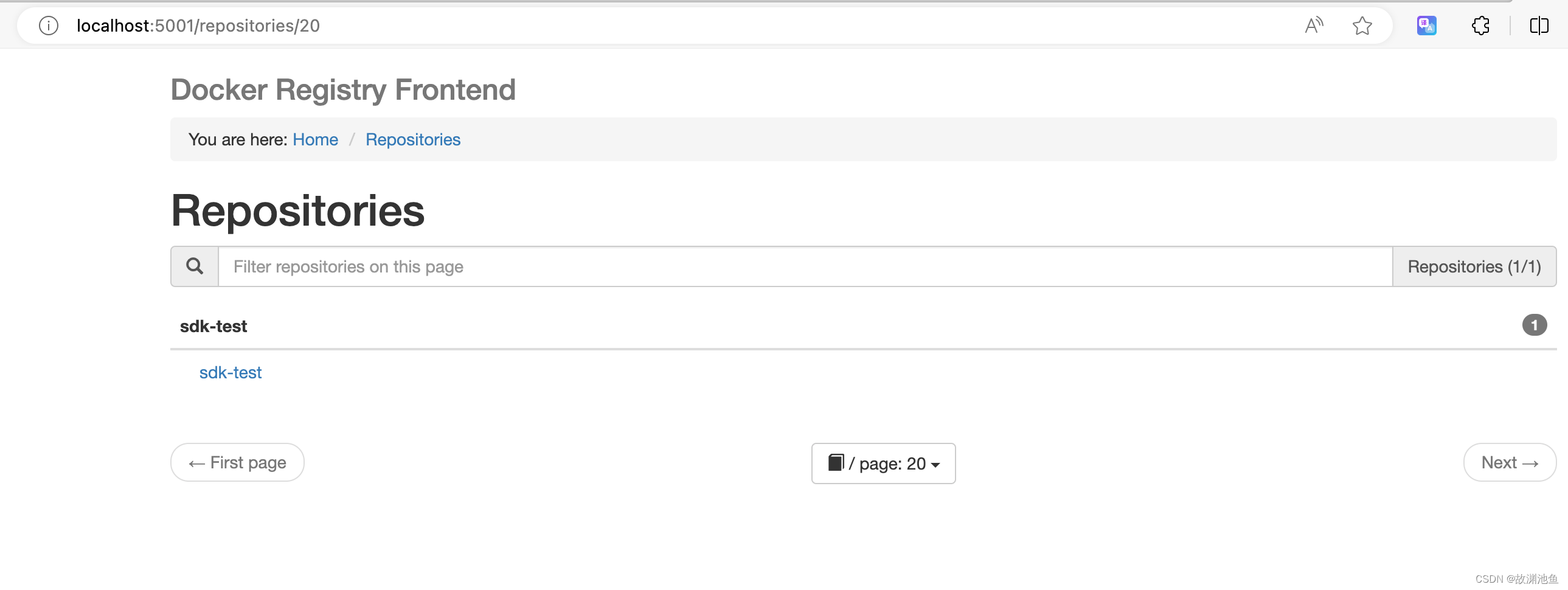
MacOS搭建docker本地私有镜像库
相关环境 macOS: bigsur 11.7.8 docker desktop: 4.22.0 docker engine: 24.0.5 准备工作 本机已经安装好docker desktop,未安装的自行参考其他教程。如果不能翻墙,可以修改本地的镜像地址,可在docker desktop 设置中的docker engine中修…...
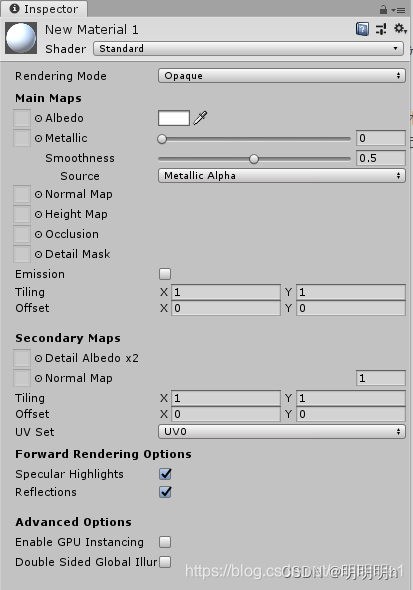
Unity Material(材质)、Texture(纹理)、Shader(着色器)简介
文章目录 一、概念二、Rendering Mode三、Main Maps三、参考文章 一、概念 Material(材质):物体的“色彩”、“纹理”、“光滑度”、“透明度”、“反射率”、“折射率”、“发光度”等,材质的本质是shader的实例(载体)Texture(贴图):附件到…...
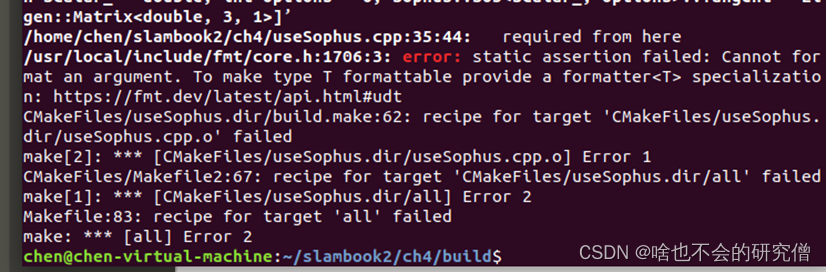
《视觉十四讲》例程运行记录(1)—— 课本源码下载和3rdparty文件夹是空的解决办法
提示:文章写完后,目录可以自动生成,如何生成可参考右边的帮助文档 文章目录 前言一、第二版十四讲课本源码下载1. 安装git工具 二、Pangolin下载和安装1. 源码下载2. Pangolin的安装(1) 安装依赖项(2) 源码编译安装(2) 测试是否安装成功 二、…...

VLM与基础分割模型的联合使用
最近做的项目里有涉及大模型,里面有一部分的功能是: 将图片输入VLM(视觉语言模型,我使用的是llava),询问图中最显著的物体,将其给出的答案作为基础分割模型(我使用的是Grounded-SAM)的text prom…...

JS数组去重的方法
目录 1、includes 2、indexOf 3、Set结合Array.from 4、filter 5、reduce 6、使用双重for循环 介绍一下数组常用的去重复方法 以以下数组为例子来介绍,一维的数字类型数组: const arr [1, 2, 2, 2, 3, 1, 6, 4, 4, 6, 5, 7] 1、includes funct…...
Go实战训练之Web Server 与路由树
Server & 路由树 Server Web 核心 对于一个 Web 框架,至少要提供三个抽象: Server:代表服务器的抽象Context:表示上下文的抽象路由树 Server 从特性上来说,至少要提供三部分功能: 生命周期控制&…...

C#中接口设计相关原则
在C#中,接口(Interface)是一种引用类型,它定义了一个契约,指定了一个类必须实现的成员(属性、方法、事件、索引器)。接口不提供这些成员的实现,只指定成员必须按照特定的方式被实现。…...
Pytorch学习笔记——卷积操作
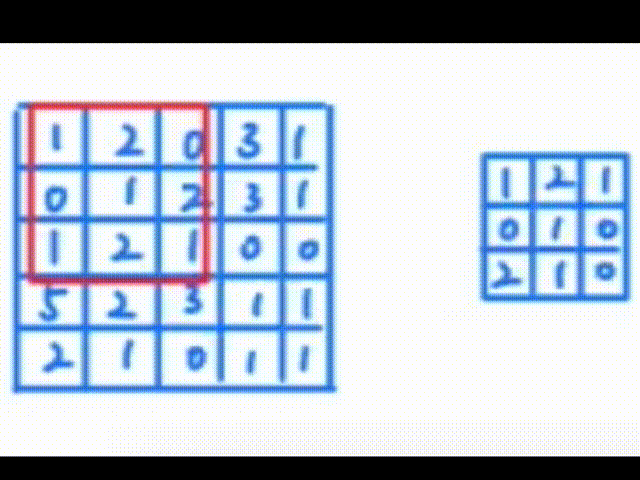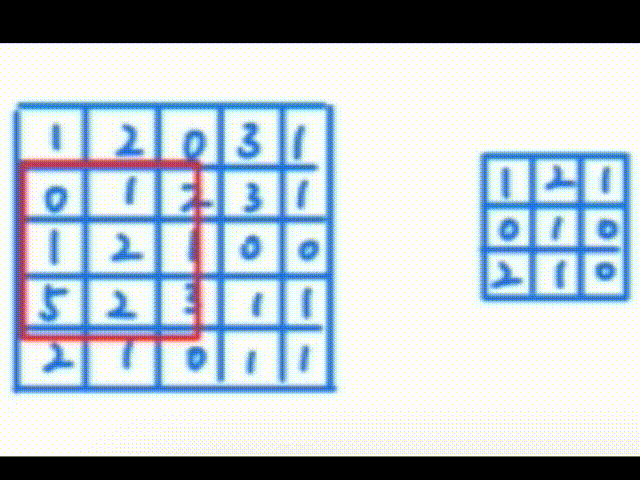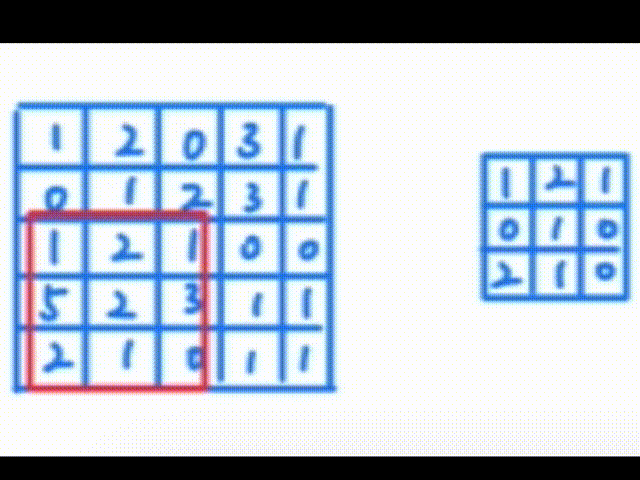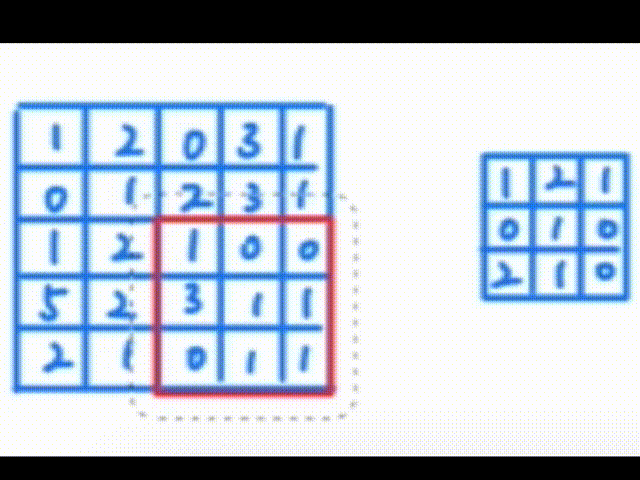
一、认识卷积操作 卷积操作是一种数学运算,它涉及两个函数:输入函数(通常是图像)和卷积核(也称为滤波器或特征检测器)。卷积核在输入函数上滑动,将核中的每个元素与其覆盖的输入函数区域中的对应…...

探索鸿蒙开发:鸿蒙系统如何引领嵌入式技术革新
嵌入式技术已经成为现代社会不可或缺的一部分。而在这个领域,华为凭借其自主研发的鸿蒙操作系统,正悄然引领着一场技术革新的浪潮。本文将探讨鸿蒙开发的特点、优势以及其对嵌入式技术发展的深远影响。 鸿蒙操作系统的特点 鸿蒙,作为华为推…...
chrome extension插件替换网络请求中的useragent
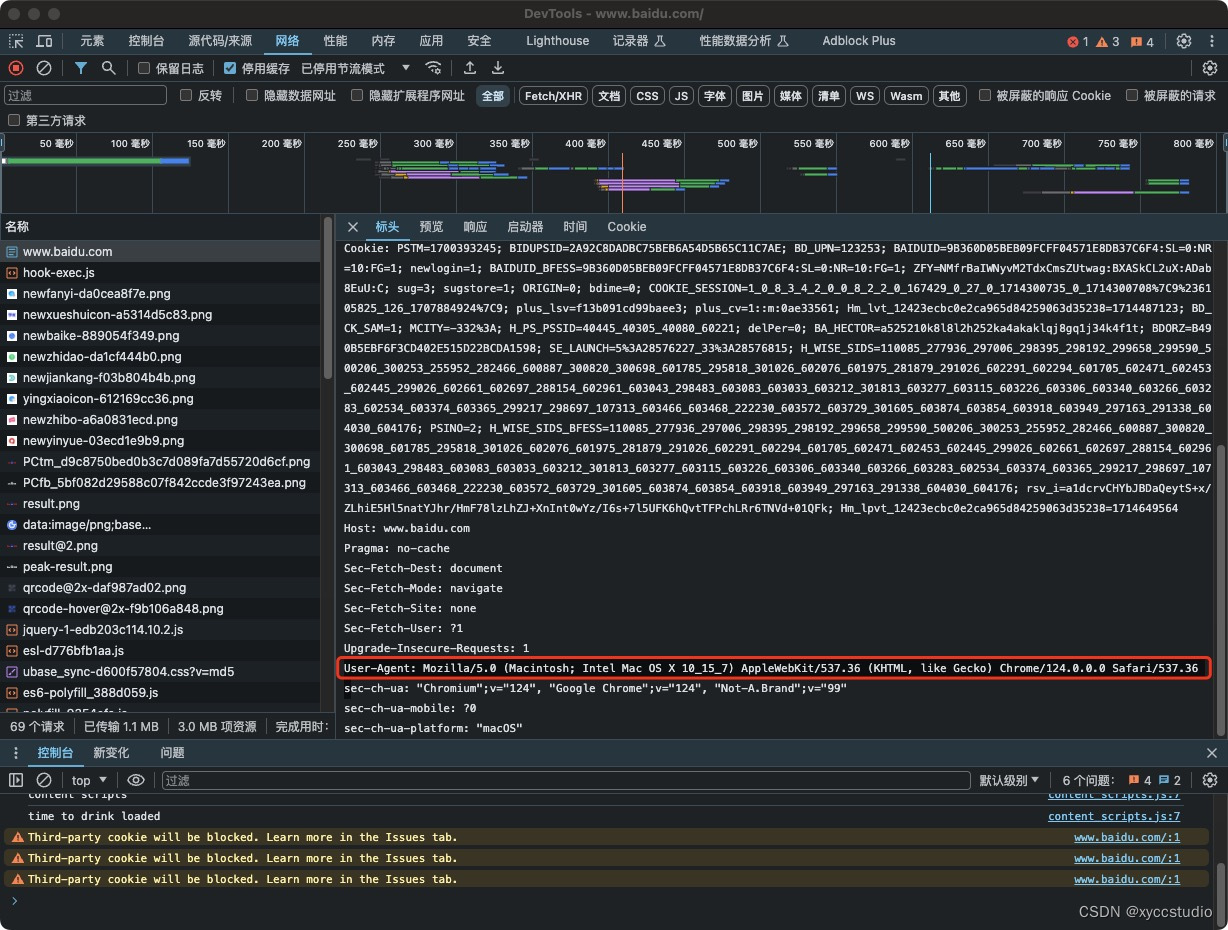
感觉Chrome商店中的插件不能很好的实现自己想要的效果,那么就来自己动手吧。 本文以百度为例: 一般来说网页请求如下: 当前使用的useragent是User-Agent: Mozilla/5.0 (Macintosh; Intel Mac OS X 10_15_7) AppleWebKit/537.36 (KHTML, like Gecko) Chrome/124.0.0.0 Safar…...

PHP基础【介绍,注释,更改编码,赋值,数据类型】
源码 <?php //单行注释 /* 多行注释 *///通过header()函数发送http头的请求信息用来指定页面的字符集编码 header("Content-type:text/html;Charsetutf-8"); //告诉浏览器,当前页面的内容类型是HTML,并且页面内容使用的是UTF-8编码。//ph…...
ASP.NET小型证券术语解释及翻译系统的设计与开发
摘 要 在系统设计上,综合各种翻译类型网站优缺点,设计出具有任何使用者都可添加术语信息的且只有管理员能够实现术语修改及删除等独特方式的术语查看管理系统。此方式能够使术语量快速增大,并且便于使用者及管理员操作,满足相互…...
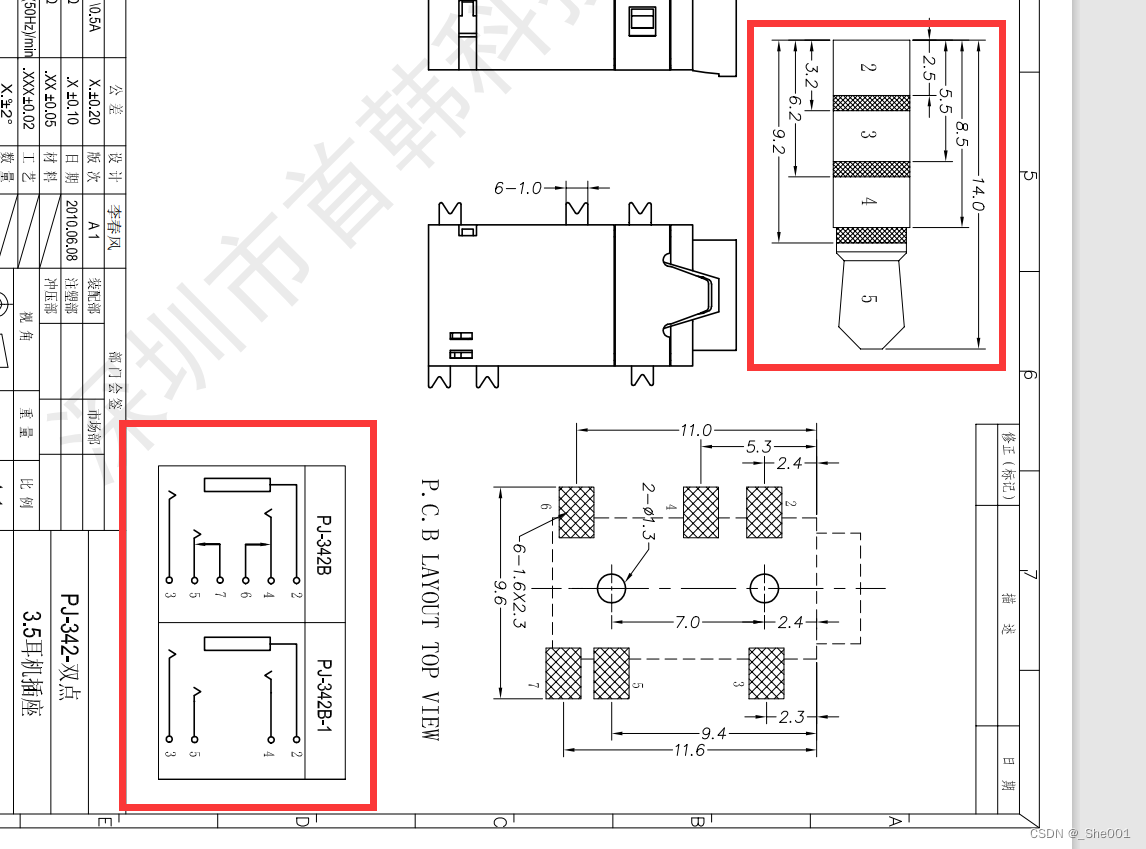
硬件知识积累 音频插座的了解,看音频插座的原理图来了解音频插座的引脚。
1. 音频接口 音频插座是一种用于连接音频信号线路的电子元件,常见于音频设备(如音响、耳机、话筒等)中。它的主要作用是将电子信号转化为声音信号,以满足人们对于音乐、电影、游戏等方面的需求。 根据插头形状的不同,音…...
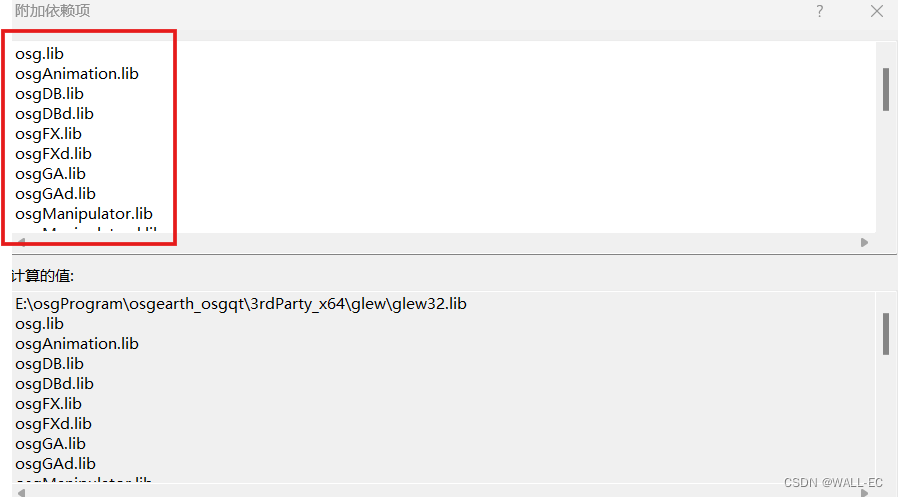
error LNK2001: 无法解析的外部符号 “__declspec(dllimport) public: __cdecl ......
运行程序时,报如上图所示错误,其中一条是: ReflectionProbe.obj : error LNK2001: 无法解析的外部符号 "__declspec(dllimport) public: __cdecl osg::Object::Object(bool)" (__imp_??0ObjectosgQEAA_NZ) 报这个错误一般是因为…...

邮箱Webhook API发送邮件的性能怎么优化?
邮箱Webhook API发送邮件的步骤?如何用邮箱API发信? 随着业务规模的扩大,如何高效地通过邮箱Webhook API发送邮件,成为了许多企业面临的关键问题。下面,AokSend将探讨一些优化邮箱Webhook API发送邮件性能的方法。 邮…...

并发编程实现
一、并行编程 1、Parallel 类 Parallel类是System.Threading.Tasks命名空间中的一个重要类,它提供数据并行和任务并行的高级抽象。 For和ForEach Parallel类下的For和ForEach对应着普通的循环和遍历(普通的for和foreach),但执行时会尝试在多个线程上…...
基于EBAZ4205矿板的图像处理:12图像二值化(阈值可调)
基于EBAZ4205矿板的图像处理:12图像二值化(阈值可调) 我的项目是基于EBAZ4205矿板的阈值可调的图像阈值二值化处理,可以通过按键调整二值化的阈值,key1为阈值加1,key4为阈值减1,key2为阈值加10,key5为阈值…...
)
椭圆曲线密码学(ECC)
一、ECC算法概述 椭圆曲线密码学(Elliptic Curve Cryptography)是基于椭圆曲线数学理论的公钥密码系统,由Neal Koblitz和Victor Miller在1985年独立提出。相比RSA,ECC在相同安全强度下密钥更短(256位ECC ≈ 3072位RSA…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

渗透实战PortSwigger靶场-XSS Lab 14:大多数标签和属性被阻止
<script>标签被拦截 我们需要把全部可用的 tag 和 event 进行暴力破解 XSS cheat sheet: https://portswigger.net/web-security/cross-site-scripting/cheat-sheet 通过爆破发现body可以用 再把全部 events 放进去爆破 这些 event 全部可用 <body onres…...

dedecms 织梦自定义表单留言增加ajax验证码功能
增加ajax功能模块,用户不点击提交按钮,只要输入框失去焦点,就会提前提示验证码是否正确。 一,模板上增加验证码 <input name"vdcode"id"vdcode" placeholder"请输入验证码" type"text&quo…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

EtherNet/IP转DeviceNet协议网关详解
一,设备主要功能 疆鸿智能JH-DVN-EIP本产品是自主研发的一款EtherNet/IP从站功能的通讯网关。该产品主要功能是连接DeviceNet总线和EtherNet/IP网络,本网关连接到EtherNet/IP总线中做为从站使用,连接到DeviceNet总线中做为从站使用。 在自动…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...
