Universal Thresholdizer:将多种密码学原语门限化
参考文献:
- [LS90] Lapidot D, Shamir A. Publicly verifiable non-interactive zero-knowledge proofs[C]//Advances in Cryptology-CRYPTO’90: Proceedings 10. Springer Berlin Heidelberg, 1991: 353-365.
- [Shoup00] Shoup V. Practical threshold signatures[C]//Advances in Cryptology—EUROCRYPT 2000: International Conference on the Theory and Application of Cryptographic Techniques Bruges, Belgium, May 14–18, 2000 Proceedings 19. Springer Berlin Heidelberg, 2000: 207-220.
- [AJL+12] Asharov G, Jain A, López-Alt A, et al. Multiparty computation with low communication, computation and interaction via threshold FHE[C]//Advances in Cryptology–EUROCRYPT 2012: 31st Annual International Conference on the Theory and Applications of Cryptographic Techniques, Cambridge, UK, April 15-19, 2012. Proceedings 31. Springer Berlin Heidelberg, 2012: 483-501.
- [BGI15] Boyle E, Gilboa N, Ishai Y. Function secret sharing[C]//Annual international conference on the theory and applications of cryptographic techniques. Berlin, Heidelberg: Springer Berlin Heidelberg, 2015: 337-367.
- [CM15] Clear M, McGoldrick C. Multi-identity and multi-key leveled FHE from learning with errors[C]//Advances in Cryptology–CRYPTO 2015: 35th Annual Cryptology Conference, Santa Barbara, CA, USA, August 16-20, 2015, Proceedings, Part II 35. Springer Berlin Heidelberg, 2015: 630-656.
- [GVW15] Gorbunov S, Vaikuntanathan V, Wichs D. Leveled fully homomorphic signatures from standard lattices[C]//Proceedings of the forty-seventh annual ACM symposium on Theory of computing. 2015: 469-477.
- [GHK+17] Goyal R, Hohenberger S, Koppula V, et al. A generic approach to constructing and proving verifiable random functions[C]//Theory of Cryptography: 15th International Conference, TCC 2017, Baltimore, MD, USA, November 12-15, 2017, Proceedings, Part II 15. Springer International Publishing, 2017: 537-566.
- [BGG+18] Boneh D, Gennaro R, Goldfeder S, et al. Threshold cryptosystems from threshold fully homomorphic encryption[C]//Advances in Cryptology–CRYPTO 2018: 38th Annual International Cryptology Conference, Santa Barbara, CA, USA, August 19–23, 2018, Proceedings, Part I 38. Springer International Publishing, 2018: 565-596.
- PZK via OWF
- LSSS & MSP
- Threshold FHE
- Multi-key FHE
文章目录
- Centralized ThFHE
- Definition
- ThFHE from Special LSSS
- ThFHE from Shamir SSS
- Decentralized ThFHE
- Universal Thresholdizer
- Definition
- UT from PZK
- UT from HS
- Threshold Cryptosystems from UT
- Function Secret Sharing
- Threshold Signatures
- Others
[BGG+18] 基于 门限同态加密,给出了构造 各种门限密码系统的一种通用方法。
Centralized ThFHE
Definition
[BGG+18] 首先给出了 threshold fully homomorphic encryption (ThFHE) for any class of access structures 的接口以及相关属性的定义。这个定义是中心化的,它有一个可信的 Setup 阶段,用于生成公私钥对以及分发私钥。
接口为:

我们要求 ThFHE 具有:紧凑性、计算正确性、语义安全性(IND-CPA)、模拟安全性(更强)


接下来,[BGG+18] 使用了 [AJL+12] 的噪声洪泛策略:为了防止 partial decryption 泄露参与者的 secret share 信息,他们根据 Smudging Lemma,对部分解密的结果(本来噪声的界 B B B)添加上超多项式大小的噪声(污染噪声的界 B s m B_{sm} Bsm 满足 B / B s m = n e g l ( λ ) B/B_{sm}=negl(\lambda) B/Bsm=negl(λ)),这使得包含私钥信息与否的两个分布的统计距离是可忽略的,从而证明模拟安全性。
[AJL+12] 使用的是形如 s = ∑ i = 1 N s i s = \sum_{i=1}^N s_i s=∑i=1Nsi 的 additive SSS。根据 FHE 的双线性(内积)解密特点,它在重构时的噪声累积是线性的,但是它只能处理 ( N − 1 ) (N-1) (N−1)-out-of- N N N 访问结构。
[BGG+18] 考虑了任意的门限访问结构(threshold access structures , TAS)

为了构造 ThFHE,首先需要一个底层的 FHE,要求它具有:紧凑性、正确性、安全性。[BGG+18] 特别地要求它的解密函数可以明确地分为线性部分以及非线性部分,

ThFHE from Special LSSS
为了减小 LSSS 重建时的噪声累加,[BGG+18] 提出了一类特殊的访问结构,称之为 {0,1}-LSSS 访问结构族,它可以被一些重构系数要么是零要么是壹的 LSSS 所支持。

这个 {0,1}-LSSS 访问结构族包含了所有可以由 monotone Boolean formulas(MBFs)计算的那些访问结构(只含 AND 以及 OR 的布尔函数,不含 NOT)。特别地,TAS 也包含在内。也就是说 Special LSSS 依旧足够的富有,
TAS ⊆ MBF ⊆ { 0 , 1 } -LSSS \text{TAS} \subseteq \text{MBF} \subseteq \{0,1\}\text{-LSSS} TAS⊆MBF⊆{0,1}-LSSS
LSSS 等价于 MSP,分发的 SS 都是由 secret 以及 random 组成的向量和某个 LSSS 矩阵相乘来获得的。各个参与者最终会拿到和 LSSS 矩阵的某些行相关的一个向量。[BGG+18] 将那些被 MSP 接受的那些行的 indices 称为 valid share set,将它们对应的参与者称为 valid party set,可对应地定义两者的 maximal invalid set 以及 minimal valid set。
基于 Special FHE 以及 Special LSSS,构造 ThFHE 如下:

选择的参数应当满足: B + l ⋅ B s m ≤ q / 4 B+l\cdot B_{sm} \le q/4 B+l⋅Bsm≤q/4 以及 B / B s m = n e g l ( λ ) B/B_{sm} = negl(\lambda) B/Bsm=negl(λ),从而需要设置超多项式大小的洪泛噪声的上界 B s m B_{sm} Bsm 以及超多项式大小的底层 FHE 密文模数 q q q,安全假设是超多项式因子的近似格问题的困难性。可以证明构造出的 ThFHE 满足:紧凑性、计算正确性、语义安全性、模拟安全性。
ThFHE from Shamir SSS
使用 LSSS 的一个缺点就是它的 SS 规模太大了,对于 TAS 的描述需要 O ( N 5.2 ) O(N^{5.2}) O(N5.2) 大小的单调公式。而 Shamir SS 的规模是和 secret 大小相同的。但是如果直接使用 Shamir SSS,它的拉格朗日插值系数需要除法(在 Z q \mathbb Z_q Zq 上求逆元,范数往往很大),这导致噪声快速累计从而无法正确解密。
[BGG+18] 使用了 [Shoup00] 的 clearing out denominators(清理分母)策略:限制各个 party 的插值点为 x = 1 , 2 , ⋯ , N x=1,2,\cdots,N x=1,2,⋯,N,特别地 dealer 插值点是 0 0 0,那么授权集 S ⊆ A t ∪ { 0 } S \subseteq \mathbb A_t \cup \{0\} S⊆At∪{0} 的 Lagrange coefficients 形如:
λ i j S = ∏ k ∈ S \ { i } ( j − k ) ∏ k ∈ S \ { i } ( i − k ) ∈ Q \lambda_{ij}^S = \frac{\prod_{k \in S\backslash\{i\}}(j-k)}{\prod_{k \in S\backslash\{i\}}(i-k)} \in \mathbb Q λijS=∏k∈S\{i}(i−k)∏k∈S\{i}(j−k)∈Q
它们被用于计算 s j = ∑ i ∈ S λ i j S ⋅ s i s_j = \sum_{i \in S} \lambda_{ij}^S \cdot s_i sj=∑i∈SλijS⋅si,其中 i ∈ S i \in S i∈S 是授权集内的参与者,而 j ∈ { 1 , 2 , ⋯ , N } \ S j \in \{1,2,\cdots,N\}\backslash S j∈{1,2,⋯,N}\S 是其他参与者。容易看出这些插值系数的分母都整除 Δ = ( N ! ) 2 \Delta = (N!)^2 Δ=(N!)2,因此 Δ ⋅ λ i j S ∈ Z \Delta \cdot \lambda_{ij}^S \in \mathbb Z Δ⋅λijS∈Z 是整数,并且上界是 ∣ Δ ⋅ λ i j S ∣ ≤ ( N ! ) 3 |\Delta \cdot \lambda_{ij}^S| \le (N!)^3 ∣Δ⋅λijS∣≤(N!)3,它们都是低范数的整数。
基于 Special FHE 以及 Shamir SSS,构造 ThFHE 如下:

选择的参数应当满足: B + ( N ! ) 3 ⋅ N ⋅ B s m ≤ q / 4 B+(N!)^3\cdot N\cdot B_{sm} \le q/4 B+(N!)3⋅N⋅Bsm≤q/4 以及 B / B s m = n e g l ( λ ) B/B_{sm} = negl(\lambda) B/Bsm=negl(λ),这也需要超多项式近似因子的困难假设。可以证明构造出的 ThFHE 满足:计算正确性、语义安全性、模拟安全性。但是它不满足紧凑性,因为密文模数的规模和 N N N 有关,比特长度的增长因子是 O ( N log N ) O(N \log N) O(NlogN)
Decentralized ThFHE
上述的 ThFHE 是中心化的,它在很多场景下有限制。除了是否存在可信方这个问题,还有参与者动态地加入和退出的情况,这导致 Setup 的频繁执行。
[BGG+18] 定义了一个去中心化的版本,记为 dThFHE,它没有 Setup 阶段。为了实现门限,他们在 Enc 算法中让各个参与者独立地生成 FHE 私钥及其 SS,然后再利用 PKE 封装这些 SS 到密文中。接口为:

类似的,定义它的一些属性:计算正确性、语义安全、模拟安全。由于 dThFHE 密文中需要包含给各个参与者的 SS 的 PKE 加密,因此密文规模一定会和 N N N 有关,因此定义了弱紧凑性。这些属性的定义我就不抄过来了,太繁琐。
构造如下:

它是一个满足各项属性的 dThFHE 方案。注意 TFHE.Setup 必须在每次 Enc 时独立地生成,因为它的私钥已经被分发在了密文中的 PKE 部分,不应该复用。所以,即使是单个参与者生成的不同密文,它们之间也无法相互作用。
不过,如果将底层的 FHE 替换为 [CM15] 提出的 Multi-Key FHE,那么获得的 MK dThFHE 是可以数据交互的。对于 ThFHE.Setup 生成独立的公私钥,它们的密文总可以先利用 masking system 转换成某组参与者对应的 expanded ciphertext,然后这些扩展的密文互相之间可以运算,最后解密时需要这组参与者中每个人的 FHE 私钥,这被从 PKE 密文中恢复出来。
Universal Thresholdizer
Definition
[BGG+18] 利用 ThFHE 给出了其他密码学原语的门限版本的通用构造:门限转化器(universal thresholdizer, UT)
他们把 Setup 和 Enc 合并(使用 ThFHE 加密 secret 作为 pp 的一部分),把 Eval 和 PartDec 合并(各个参与者对这个 secret 密文做同一个运算,然后部分解密),并添加了 PartVerify 提供鲁棒性。确切地说,UT 提供了这样的一个功能:由 dealer 分发 ThFHE 私钥,同时 dealer 还用 ThFHE 加密某个秘密 x x x 获得 c t ( x ) ct(x) ct(x) 密文;接着对于公开的某个电路 C C C,各个 party 同态计算出 c t ( C ( x ) ) ct(C(x)) ct(C(x)),然后立即部分解密得到 p i p_i pi,它们是计算结果 C ( x ) C(x) C(x) 的一组 SS;最终这些 SS 可以合成为 C ( x ) C(x) C(x) 本身。即 UT 把关于秘密 x x x 的电路 C C C 给 “门限化” 了,只有满足访问结构的一组参与者同时计算 C ( x ) C(x) C(x) 以获得它的 SS,才能最终获得 C ( x ) C(x) C(x) 结果,这里的 x x x 是被 Setup 固定到 pp 里的,而公开的电路 C C C 可以随意变化。
UT 的接口为:

紧凑性、计算正确性、验证正确性:

鲁棒性:

模拟安全性:

UT from PZK
带预处理的 ZKP 系统(zero knowledge proof system with pre-processing, PZK)是 NIZK 的弱化,它的存在性只需要比 NIZK 所要求的弱得多的假设。PZK 只有最后一轮通信需要从 Prover 发往 Verifier,之前的所有通信轮次都可以被双方离线计算。

[BGG+18] 利用 ThFHE、PZK 系统(证明执行了正确的计算)、非交互的承诺(绑定 ThFHE 私钥的 SS),给出了 UT 的构造。
- [LS90] 在 OWF 存在的假设下,给出了 NIZK with CRS 的构造,我们可以根据 LWE 问题来构造 OWF(虽然效率会很低)
- [GHK+17] 基于(超多项式近似因子的) LWE 假设,构造了 non-interactive commitments,因此并不引入新的假设。
构造如下:

可以证明它满足 UT 所要求的各种属性。
UT from HS
同态签名(homomorphic signature, HS)允许在签名上执行同态运算,可用于证明 y y y(生成 y y y 的签名)确实是 x x x(已经被签名)在电路 C C C(公开的)上正确计算的。它的接口是:

HS 的功能是:

假设 SIS 困难,[GVW15] 给出了 (Leveled) FHS 的构造。因此利用 HS 提供 UT 的鲁棒性,也只需要格上困难问题,并没有引入新的假设。这篇文章我还没看,具体的构造,略。
HS 比 NIZK 更加紧凑,并且可以直接基于 LWE 构造出来,因此将它应用到 UT 的构造中替换 NIZK 以提供鲁棒性,在性能上会更好一些。容易把上述的 UT from PZK 修改为 UT from HS,略。
Threshold Cryptosystems from UT
[BGG+18] 利用 Universal Thresholdizer,将其他的多种密码原语转换成对应的门限版本。
Function Secret Sharing
[BGI15] 提出了函数秘密分享(Function Secret Sharing, FSS),类似于 SSS,但是分发的不再是消息,而是去分发函数。接口是:

紧凑性、计算正确性、安全性:

利用 UT 以及 PRF,可以给出 FSS 的构造。简记 U ( f , x ) \mathcal U(f,x) U(f,x) 是计算 f ( x ) f(x) f(x) 的通用电路(universal circuit),简记 U x \mathcal U_x Ux 是硬编码 x x x 的电路。

Threshold Signatures
门限签名是把 signing key 分发给多个签名者,只有满足某访问结构的签名者小组可以共同生成一个合法的签名。

紧凑性、计算正确性、部分验签正确性:

(弱)不可伪造性:

鲁棒性、匿名性:

使用 UT 将底层 Sign 门限化,

Others
[BGG+18] 还利用 UT 给出了:CCA Threshold PKE,Compact ThFHE, Threshold Distributed PRFs
基本的思路都是:对于携带秘密的原始电路 C ( k , s ) C(k,s) C(k,s),将它的秘密 k k k 使用 UT.Setup 分发,然后使用 UT.Eval 对硬编码了字符串 s s s 的电路关于这些秘密的 SS 做运算,生成了运算结果的 SS,最后再用 UT.Combine 将它们组合成最终的结果。
相关文章:

Universal Thresholdizer:将多种密码学原语门限化
参考文献: [LS90] Lapidot D, Shamir A. Publicly verifiable non-interactive zero-knowledge proofs[C]//Advances in Cryptology-CRYPTO’90: Proceedings 10. Springer Berlin Heidelberg, 1991: 353-365.[Shoup00] Shoup V. Practical threshold signatures[C…...
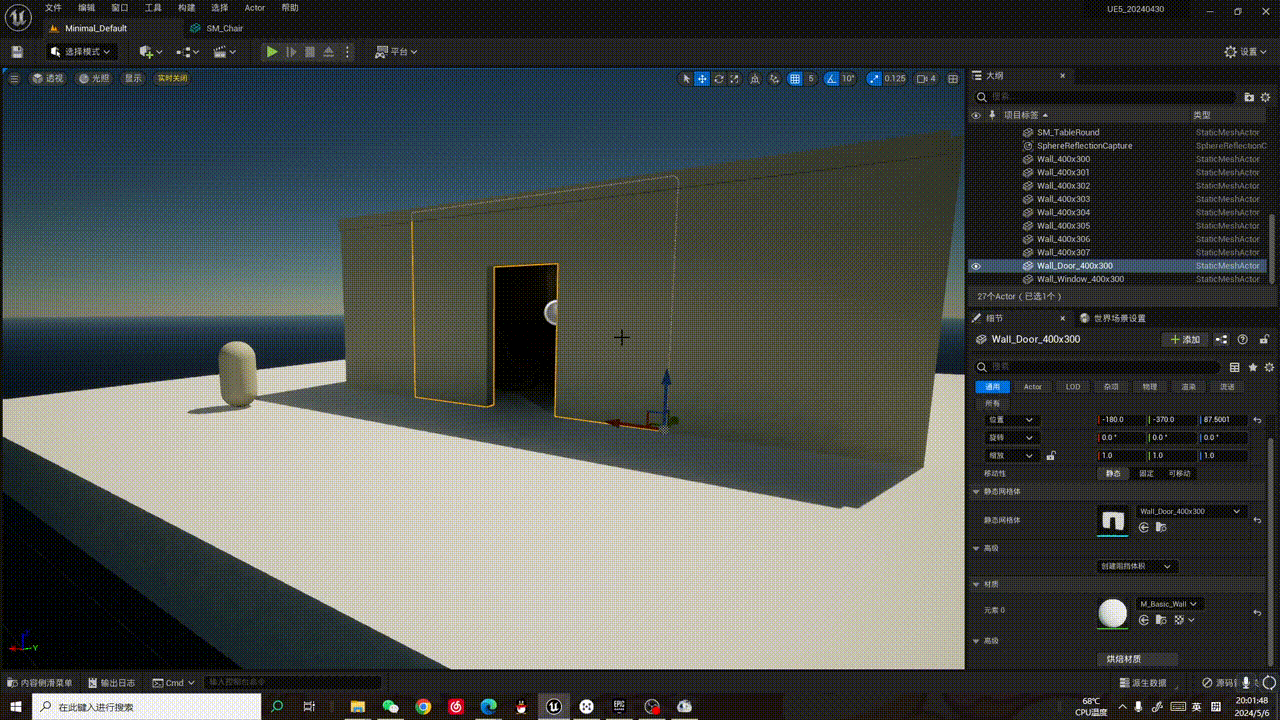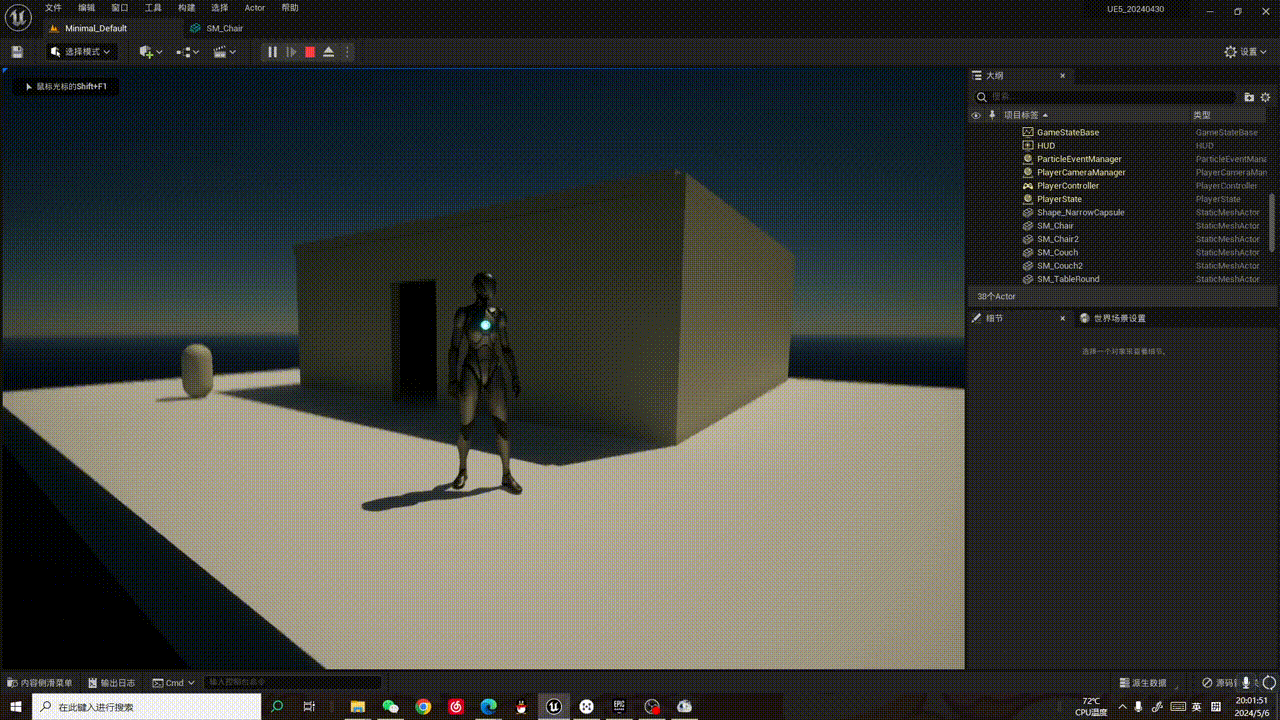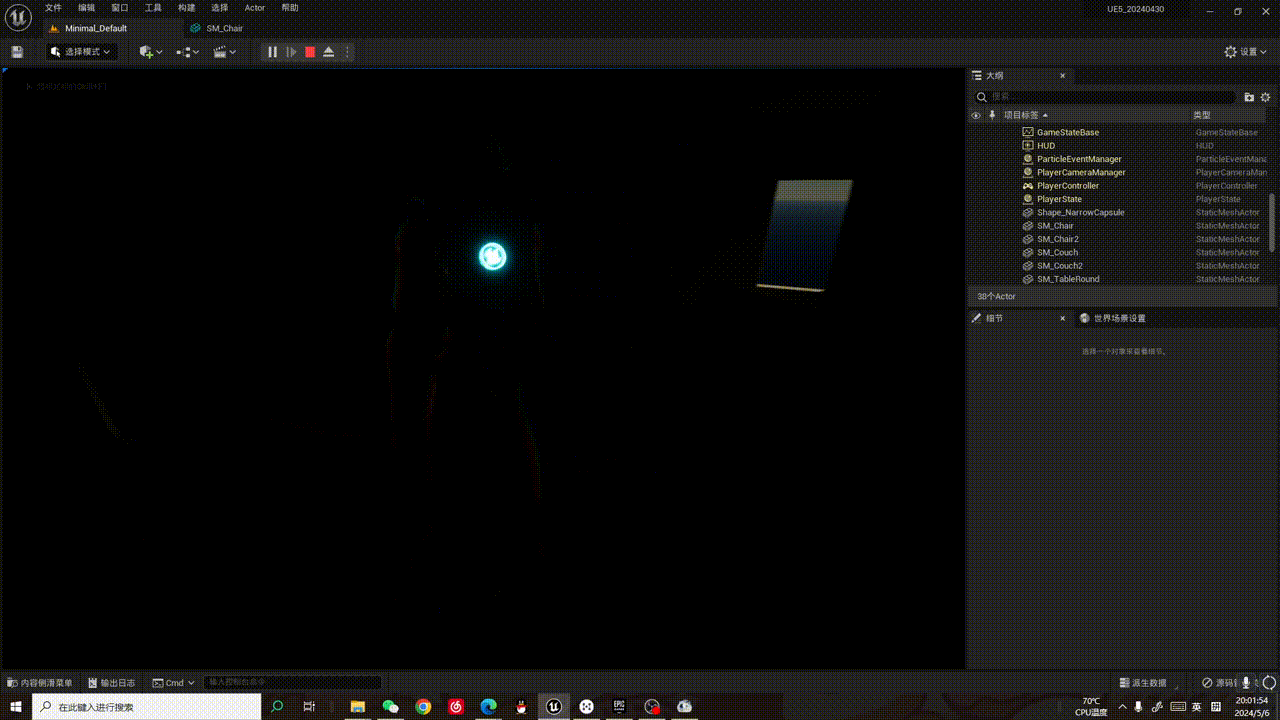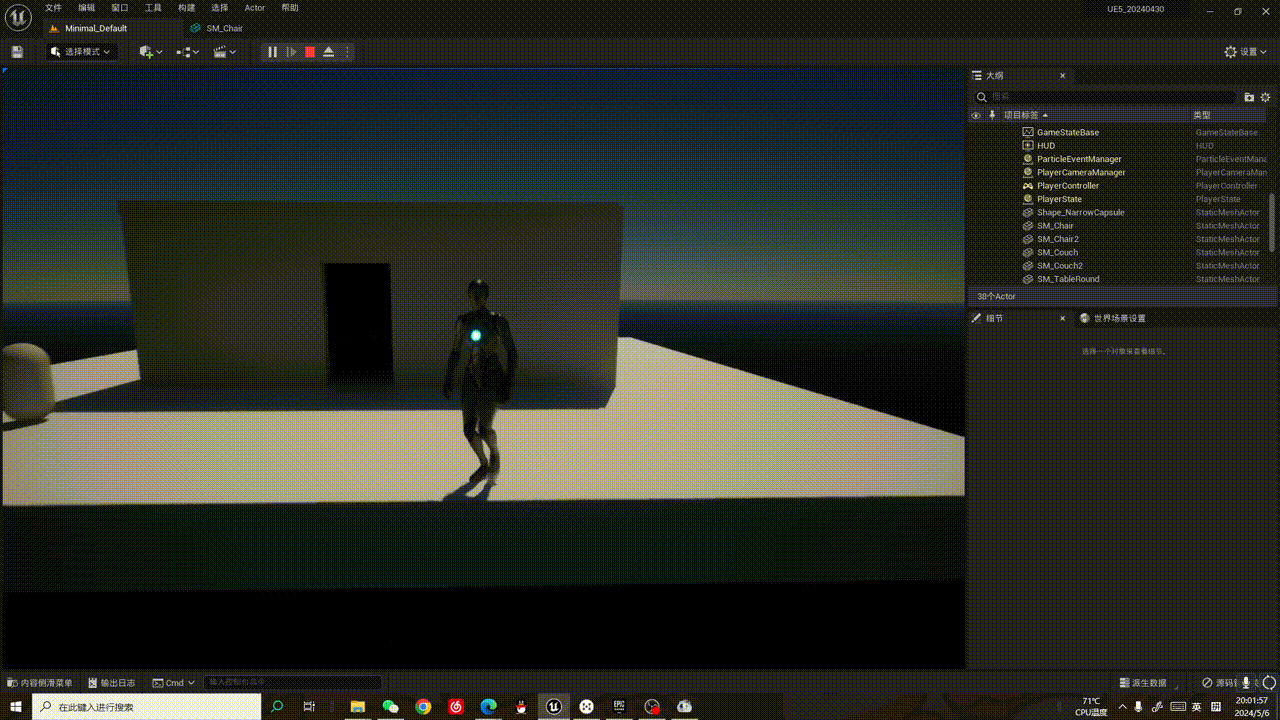
【UE5学习笔记】编辑及运行界面:关闭眼部识别(自动曝光)
自动曝光,也就是走进一个黑暗的环境,画面会逐渐变量,以模拟人眼进入黑暗空间时瞳孔放大,进光量增加的一种真实视觉感受: 制作过程中是否关闭自动曝光,取决于游戏的性质,但是个人认为,…...

未来科技的前沿:深入探讨人工智能的进展、机器学习技术和未来趋势
文章目录 一、人工智能的定义和概述1. 人工智能的基本概念2. 人工智能的发展历史 二、技术深入:机器学习、深度学习和神经网络1. 机器学习2. 深度学习3. 神经网络 三、人工智能的主要目标和功能1. 自动化和效率提升2. 决策支持和风险管理3. 个性化服务和预测未来 本…...

3-qt综合实例-贪吃蛇的游戏程序
引言: 如题,本次实践课程主要讲解贪吃蛇游戏程序。 qt贪吃蛇项目内容: 一、功能需求 二、界面设计 各组件使用: 对象名 类 说明 Widget QWidge 主窗体 btnRank QPushButton 排行榜-按钮 groupBox QGroupBox 难…...

QGraphicsView实现简易地图12『平移与偏移』
前文链接:QGraphicsView实现简易地图11『指定层级-定位坐标』 提供地图平移与偏移功能。地图平移是指将地图的中心点更改为给定的点,即移动地图到指定位置。地图偏移是指将当前视口内的地图向上/下/左/右/进行微调,这里偏移视口宽/高的四分之…...

深入探索 Vue 中的 createVNode 与 resolveComponent
在 Vue 开发中,createVNode和resolveComponent是两个至关重要的工具,它们为我们提供了强大的能力来灵活地创建和操控组件。 一、首先,让我们深入了解一下createVNode。 这是一个用于创建虚拟节点的关键函数,通过它,我…...
【记录42】centos 7.6安装nginx教程详细教程
环境:腾讯云centos7.6 需求:安装nginx-1.24.0 1. 切入home文件 cd home 2. 创建nginx文件 mkdir nginx 3. 切入nginx文件 cd nginx 4. 下载nginx安装包 wget https://nginx.org/download/nginx-1.24.0.tar.gz 5. 解压安装包 tar -zxvf nginx-1.24.0.…...

C语言程序设计(不熟悉的点)
一、switch多路分支语句 二、条件表达式 三、循环 for循环: for循环的三个表达式不是必须的,第一个表达式之前声明过,可以不写,第三个表达式可以放在循环体里面;第二个表达式可以不写,为死循环。 空循环…...

DAO是什么?有什么用途?
DAO(Decentralized Autonomous Organization,去中心化自治组织)是一种基于区块链技术的组织形式,它没有中央管理层,而是通过智能合约和区块链上的代码来运作。DAO 的决策过程是透明的,通常由组织的成员通过…...
Socket学习记录
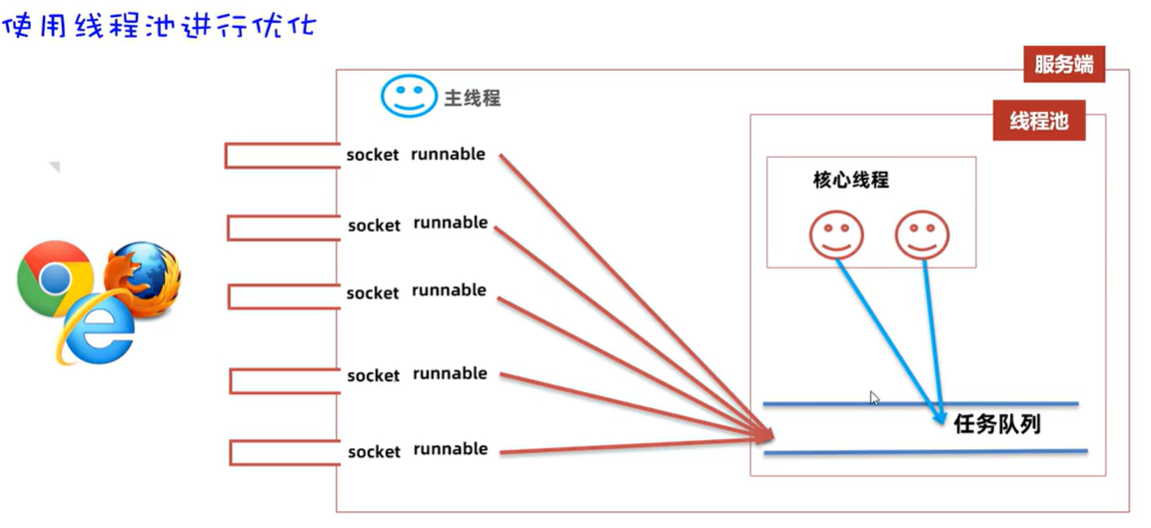
本次学习Socket的编程开发,该技术在一些通讯软件,比如说微信,QQ等有广泛应用。 网络结构 这些都是计算机网络中的内容,我们在这里简单回顾一下: UDP(User Datagram Protocol):用户数据报协议;TCP(Transmission Contr…...

黑马 - websocket搭建在线聊天室
这里写自定义目录标题 一、消息推送常见方式二、websocket 是什么?三、websocket api的介绍1、客户端 (浏览器)2、服务端api 四、实现在线聊天室1、需求2、聊天室流程分析3、消息格式4、代码实现 一、消息推送常见方式 1、轮训方式 2、SSE…...
【每日力扣】543. 二叉树的直径与101. 对称二叉树
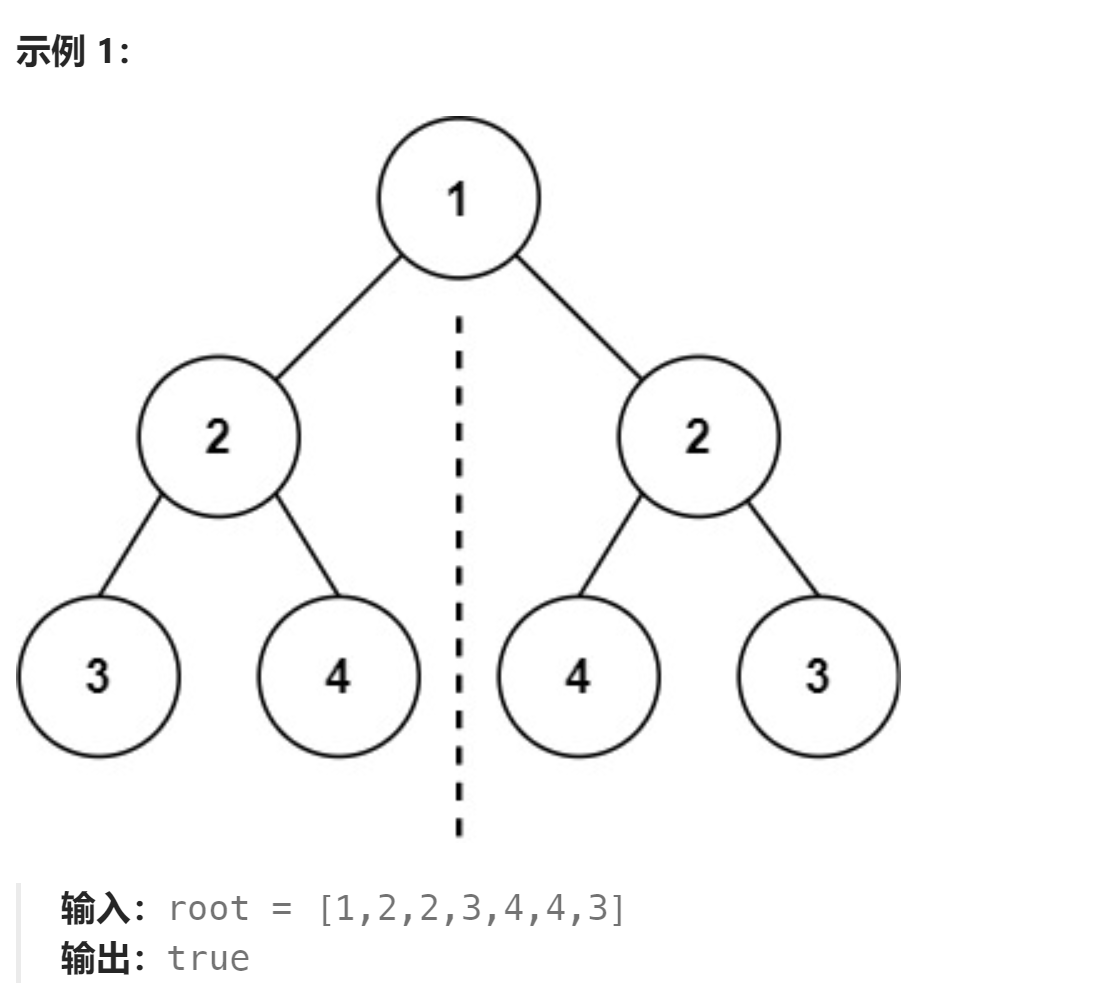
🔥 个人主页: 黑洞晓威 😀你不必等到非常厉害,才敢开始,你需要开始,才会变的非常厉害 543. 二叉树的直径 给你一棵二叉树的根节点,返回该树的 直径 。 二叉树的 直径 是指树中任意两个节点之间最长路径的…...

【linux】——日志分析
1. 日志文件 1.1 日志文件的分类 日志文件: 是用于记录Linux系统中各种运行消息的文件,相当于Linux主机的“日记". 日志文件对于诊断和解决系统中的问题很有帮助,系统一旦出现问题时及时分析日志就会“有据可查”。此外。当主机遭受攻…...
【intro】GraphSAGE
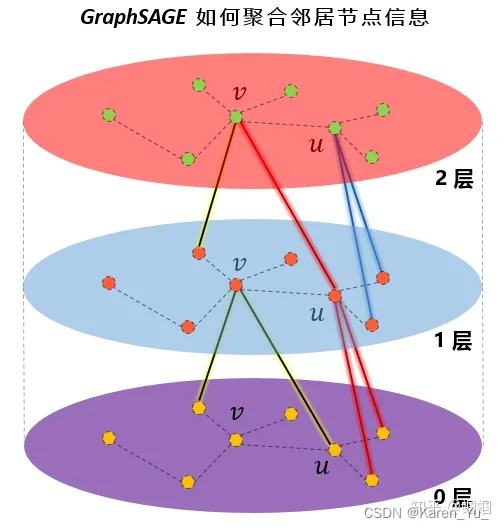
论文 https://arxiv.org/pdf/1706.02216 abstract 大图中节点的低维embedding已经被证明在各种预测任务中非常有用,然而,大多数现有的方法要求在embedding训练期间图中的所有节点都存在;这些先前的方法属于直推式(transductive)…...
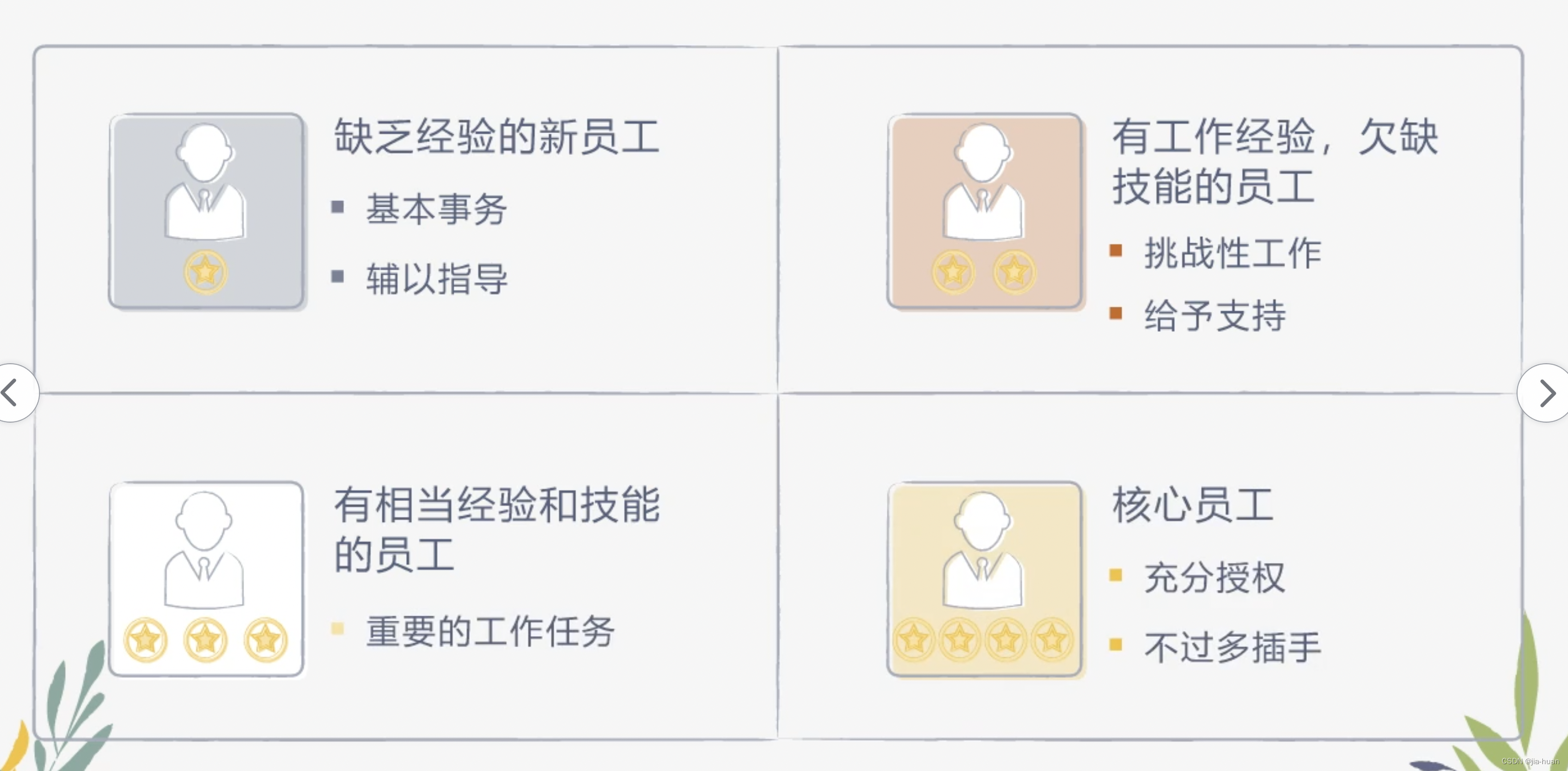
管理能力学习笔记九:授权的常见误区和如何有效授权
授权的常见误区 误区一:随意授权 管理者在授权工作时,需要依据下属的能力、经验、意愿问最自己:这项工作适合授权给Ta做吗?如果没有,可以通过哪些方法进行培训呢? 误区二:缺乏信任 心理暗示…...

第21天 反射
反射概述 想象一下,你在一个房间里边,但你看不见自己,也不知道自己是谁。这时候你面前有一个镜子,你可以通过镜子的反射来观察自己。反射就像这面镜子。它让你能够检查、分析、修改Java中的对象、类、方法等 使用情况࿱…...

多链路聚合设备是什么
多链路聚合设备属于通信指挥装备。 乾元通多链路聚合设备,它能够将多个网络链路聚合成一个逻辑链路,以实现高速、稳定、可靠的数据传输。多链路聚合设备的核心技术包括链路聚合、负载均衡、故障切换等,能够智能管理和优化利用不同网络链路&a…...
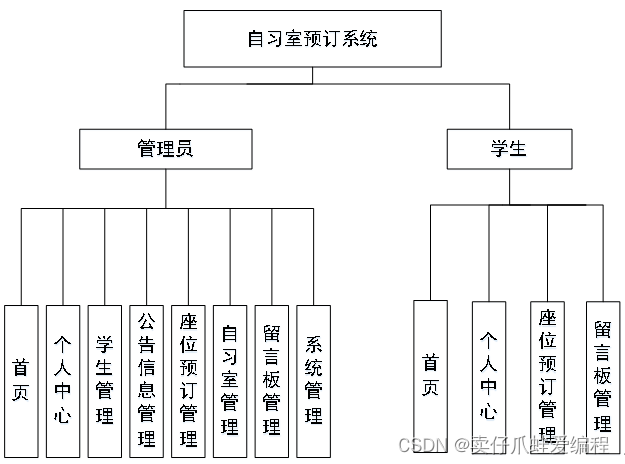
基于springboot+vue+Mysql的自习室预订系统
开发语言:Java框架:springbootJDK版本:JDK1.8服务器:tomcat7数据库:mysql 5.7(一定要5.7版本)数据库工具:Navicat11开发软件:eclipse/myeclipse/ideaMaven包:…...

解决后端ID传到前端时被截断,末尾显示00
问题原因: Java后端Long类型的取值和前端Number类型取值范围不一样。 解决方案: 将id字段进行json序列化时转为字符串。 JsonSerialize(using ToStringSerializer.class) private Long id;...

Transformer中的数据输入构造
文章目录 1. 文本内容2. 字典构造2.1 定义一个类用于字典构造2.2 拆分文本2.3 构造结果 3. 完整代码 1. 文本内容 假如我们有如下一段文本内容: Optics It is the branch of physics that studies the behaviour and properties of light . Optical Science 这段…...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

Module Federation 和 Native Federation 的比较
前言 Module Federation 是 Webpack 5 引入的微前端架构方案,允许不同独立构建的应用在运行时动态共享模块。 Native Federation 是 Angular 官方基于 Module Federation 理念实现的专为 Angular 优化的微前端方案。 概念解析 Module Federation (模块联邦) Modul…...

Spring Boot+Neo4j知识图谱实战:3步搭建智能关系网络!
一、引言 在数据驱动的背景下,知识图谱凭借其高效的信息组织能力,正逐步成为各行业应用的关键技术。本文聚焦 Spring Boot与Neo4j图数据库的技术结合,探讨知识图谱开发的实现细节,帮助读者掌握该技术栈在实际项目中的落地方法。 …...

10-Oracle 23 ai Vector Search 概述和参数
一、Oracle AI Vector Search 概述 企业和个人都在尝试各种AI,使用客户端或是内部自己搭建集成大模型的终端,加速与大型语言模型(LLM)的结合,同时使用检索增强生成(Retrieval Augmented Generation &#…...

AI语音助手的Python实现
引言 语音助手(如小爱同学、Siri)通过语音识别、自然语言处理(NLP)和语音合成技术,为用户提供直观、高效的交互体验。随着人工智能的普及,Python开发者可以利用开源库和AI模型,快速构建自定义语音助手。本文由浅入深,详细介绍如何使用Python开发AI语音助手,涵盖基础功…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...
