结合场景,浅谈深浅度拷贝
有两段代码是这样的:
A段:
List<String> list1 = new ArrayList<>();
Bear B = new Bear();
for(Apple apple : apples){B.url = apple.url;B.content = apple.content;list1.add(Bear);
}B段:
List<String> list1 = new ArrayList<>();
for(Apple apple : apples){
Bear B = new Bear();B.url = apple.url;B.content = apple.content;list1.add(Bear);
}显而易见,这两段代码的区别在于Bear对象的创建的位置不同,第一段代码里面,先创建了一个 Bear 对象 B,然后在循环中不断更新 B 的属性,并将同一个 B 对象多次添加到 list1 中。由于 list1 中存储的是对象的引用,因此最终 list1 中存储的是多个指向同一个 Bear 对象的引用。
而第二段代码中,我们在每次循环中都创建了一个新的 Bear 对象 B,并将其添加到 list1 中。因此,list1 中存储的是多个不同的 Bear 对象的引用。
所以,其实两次list的存储的Bear对象结果会是不同的,第一段代码存了一堆一样的Bear,那么问题来了:我想不重复创建Bear对象,但是也能达到第二段效果,应该怎么做?
答案是使用深度拷贝;
在修复代码之前,深浅度拷贝的定义我们复习下:
浅拷贝(Shallow Copy):
- 浅拷贝是指在复制对象时,只复制对象本身和其内部引用的对象的引用,而不复制引用的对象本身。
- 在浅拷贝中,新对象和原对象共享内部引用的对象,即新对象和原对象的引用指向同一个内部对象。
- 如果原对象的属性是基本数据类型,那么浅拷贝会复制这些属性的值;如果原对象的属性是引用类型,那么浅拷贝只会复制引用,而不会复制引用指向的对象。
深度拷贝(Deep Copy):
- 深度拷贝是指在复制对象时,不仅复制对象本身,还会递归复制对象内部引用的对象,直到所有引用的对象都被复制。
- 在深度拷贝中,新对象和原对象的所有引用对象都是独立的,即新对象和原对象的引用指向不同的内部对象。
- 无论原对象的属性是基本数据类型还是引用类型,深度拷贝都会复制所有属性的值或引用指向的对象。
原理比较:
- 浅拷贝只复制对象本身和其内部引用的对象的引用,因此新对象和原对象共享内部引用的对象,可能会导致对象之间的状态相互影响。
- 深度拷贝会递归复制对象内部引用的对象,确保新对象和原对象的所有引用对象都是独立的,避免对象之间的状态相互影响。
那么好,我们基于该原理改造下我们的第一段代码:
首先需要重写Bear对象,重写clone方法:
public class Bear implement Clone{private String url;private String content;//构造函数等省略@Overridepublic Bear clone(){try{Bear cloned = (Bear) super.clone(); // 首先调用父类的 clone 方法进行浅拷贝// 对象的属性进行深度拷贝cloned.url = new String(this.url);cloned.content = new String(this.content);return cloned; }catch(CloneNotSupportedException e){throw new AssertionError();}}}写完Bear类的clone方法后,就可以用它的clone方法来做对象复制,最终第一段代码改写如下:
List<String> list1 = new ArrayList<>();
Bear originalBear = new Bear(); // 假设有一个原始的 Bear 对象
for(Apple apple : apples){Bear clonedBear = originalBear.clone(); // 使用克隆方法创建新的 Bear 对象clonedBear.url = apple.url;clonedBear.content = apple.content;list1.add(clonedBear);
}这样修改后,可以避免多次创建新对象,同时确保 list1 中加载不同的 Bear 对象。
相关文章:

结合场景,浅谈深浅度拷贝
有两段代码是这样的: A段: List<String> list1 new ArrayList<>(); Bear B new Bear(); for(Apple apple : apples){B.url apple.url;B.content apple.content;list1.add(Bear); } B段: List<String> list1 new A…...
生成指定范围的随机整数
private static final Random RANDOM new Random();// 生成指定范围的随机整数public static int generateRandomInt(int min, int max) {return RANDOM.nextInt(max - min 1) min;}public static void main(String[] args) {Integer count 5;Integer randomInt generateR…...

少的缓存穿透是缓存击穿,大量的是缓存雪崩
只要请求穿过了缓存层,直接打到了数据库,我就把这个现象理解为缓存穿透。 只要缓存失效了,就会出现缓存穿透,然后根据失效缓存数量的多少,划分出缓存击穿和缓存雪崩 缓存一致性 先改redis再改mysql。...

设备能耗数据在线监测
在追求可持续发展和绿色经济的当下,企业对于设备能耗的管理愈发重视。设备能耗数据在线监测,不仅能帮助企业实时掌握设备的运行状况,还能为企业节能减排、降低运营成本提供有力支持。HiWoo Cloud平台凭借其先进的技术和丰富的经验,…...

springboot整合websocket,超简单入门
springBoot整合webSocket,超简单入门 webSocket简洁 WebSocket 是一种基于 TCP 协议的全双工通信协议,它允许客户端和服务器之间建立持久的、双向的通信连接。相比传统的 HTTP 请求 - 响应模式,WebSocket 提供了实时、低延迟的数据传输能力。…...

代码随想录算法训练营第三十四天| 860.柠檬水找零 406.根据身高重建队列 452. 用最少数量的箭引爆气球
860.柠檬水找零 题目链接 思路 三种情况,一种贪心,在bill为20时,有一次贪心选择:优先考虑先找105,再考虑找3*5,因为5可以用于bill10和bill20两种情况 解题方法 第一种:bill5,直接收 第二种…...
ICode国际青少年编程竞赛- Python-2级训练场-识别循环规律2
ICode国际青少年编程竞赛- Python-2级训练场-识别循环规律2 1、 for i in range(3):Dev.step(3)Dev.turnRight()Dev.step(4)Dev.turnLeft()2、 for i in range(3):Spaceship.step(3)Spaceship.turnRight()Spaceship.step(1)3、 Dev.turnLeft() Dev.step(Dev.x - Item[1].…...

12.轻量级锁原理及其实战
文章目录 轻量级锁原理及其实战1.轻量级锁的核心原理2.轻量级锁的演示2.1.轻量级锁的演示代码2.2.结果分析 3.轻量级锁的分类3.1.普通自旋锁3.2.自适应自旋锁 4.轻量级锁的膨胀 轻量级锁原理及其实战 引入轻量级锁的主要目的是在多线程环境竞争不激烈的情况下, 通过…...
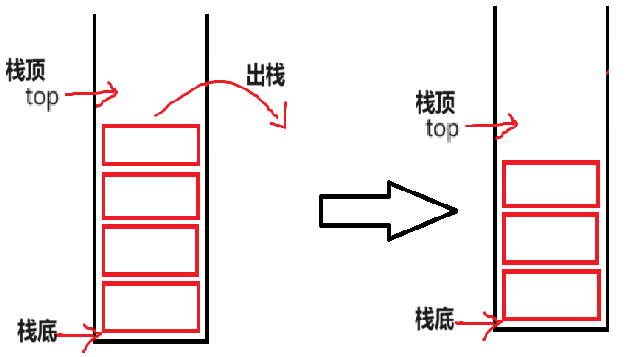
栈结构(c语言)
1.栈的概念 栈:一种特殊的线性表,其只允许在固定的一端进行插入和删除元素操作。进行数据插入和删除操作的一端称为栈顶,另一端称为栈底。栈中的数据元素遵守后进先出LIFO(Last In First Out)的原则。 压栈&am…...

【C++】C/C++中新const用法:const成员
欢迎来到CILMY23的博客 本篇主题为: C/C中新const用法:const成员 个人主页:CILMY23-CSDN博客 系列专栏:Python | C | C语言 | 数据结构与算法 | 贪心算法 | Linux 感谢观看,支持的可以给个一键三连,点赞…...

武汉凯迪正大—钢管焊缝裂纹探伤仪
产品概述 武汉凯迪正大无损探伤仪是一种便携式工业无损探伤仪器, 能够快速便捷、无损伤、精确地进行工件内部多种缺陷(裂纹、夹杂、气孔等)的检测、定位、评估和诊断。既可以用于实验室,也可以用于工程现场。 设置简单,…...

为什么 IP 地址通常以 192.168 开头?
在网络配置中,我们经常会遇到以 192.168 开头的 IP 地址,例如 192.168.0.1 或者 192.168.1.100。 这些地址通常用于局域网中,但为什么要选择以 192.168 开头呢? 本文将深入探讨这个问题,并解释其背后的原因和历史渊源…...

elementUi中的el-table合计行添加点击事件
elementUi 文档中,合计行并没有点击事件,这里自己实现了合计行的点击事件。 created() {this.propertyList [{ property: order, label: 序号 },{ property: deptName, label: 单位名称 },{ property: contentPublishQuantity, label: 文章数量 },{ pro…...

Zookeeper集群搭建的一些问题
问题描述一: Cannot open channel to 2 at election address /192.168.60.132:3888解决方案: 查看zookeeper配置文件zoo.cfg / zoo_sample.cfg中集群配置部分 server.1zoo1-net1:2888:3888|zoo1-net2:2889:3889 server.2zoo2-net1:2888:3888|zoo2-net2…...
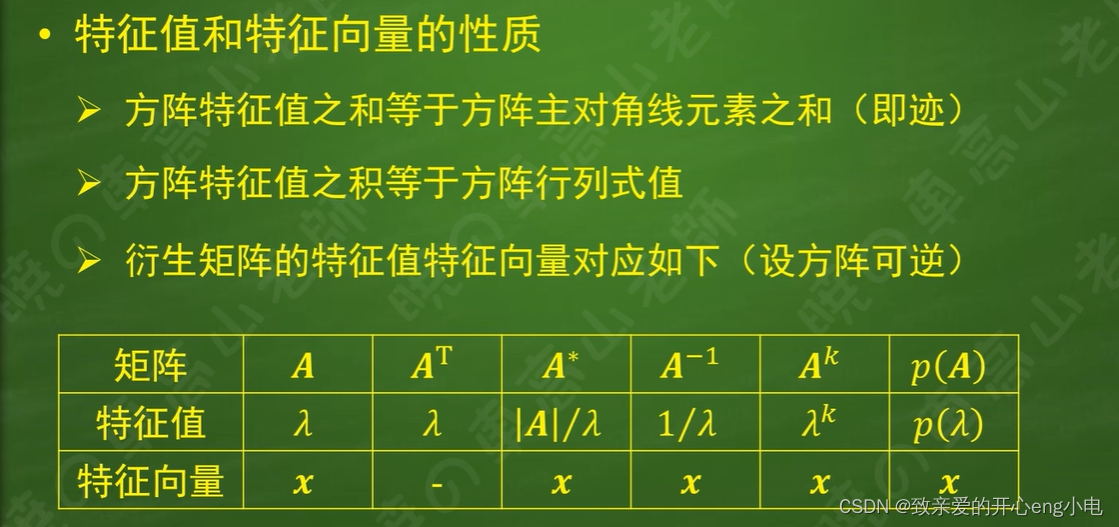
【线性代数】俗说矩阵听课笔记
基础解系的概念 线性方程组的解 21行列式和矩阵秩Rank的等价刻画 子式 标准型 利用子式求解矩阵的rank 24零积秩不等式 齐次线性方程组的基础解系 rank的两个重要结论 ¥25伴随矩阵的rank 奇异矩阵:行列式0的矩阵 31线性相关,线性无关&#…...

物联网技术在数字化工厂中的应用,你知道多少?——青创智通
工业物联网解决方案-工业IOT-青创智通 物联网(IoT)技术在数字化工厂的应用正日益成为工业革命的重要推动力。随着科技的飞速发展,物联网技术不断革新,其在数字化工厂中的应用也呈现出愈发广泛和深入的态势。本文将详细探讨物联网…...
nacos开启登录开关启动报错“Unable to start embedded Tomcat”
nacos 版本:2.3.2 2.2.2版本之前的Nacos默认控制台,无论服务端是否开启鉴权,都会存在一个登录页;在之后的版本关闭了默认登录页面,无需登录直接进入控制台操作。在这里我们可以在官网可以看到相关介绍 而我现在所用的…...
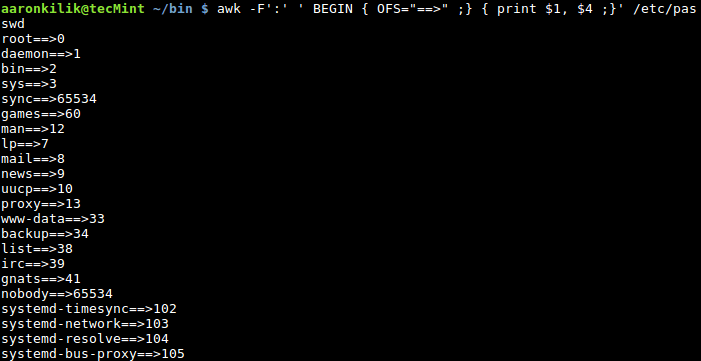
Linux|了解如何使用 awk 内置变量
引言 当我们揭开 Awk 功能部分时,我们将介绍 Awk 中内置变量的概念。您可以在 Awk 中使用两种类型的变量:用户定义的变量和内置变量。 内置变量的值已经在 Awk 中定义,但我们也可以仔细更改这些值,内置变量包括: FILEN…...

代码随想录-算法训练营day29【回溯算法05:递增子序列、全排列】
代码随想录-035期-算法训练营【博客笔记汇总表】-CSDN博客 第七章 回溯算法part05* 491.递增子序列 * 46.全排列 * 47.全排列 II详细布置 491.递增子序列 本题和大家刚做过的 90.子集II 非常像,但又很不一样,很容易掉坑里。 https://programmercarl.com…...

704. 二分查找
Problem: 704. 二分查找 🐷我的leetcode主页 文章目录 题目分类思路什么是二分查找如何理解时间复杂度 解题方法Code 题目 给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target&a…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

C# SqlSugar:依赖注入与仓储模式实践
C# SqlSugar:依赖注入与仓储模式实践 在 C# 的应用开发中,数据库操作是必不可少的环节。为了让数据访问层更加简洁、高效且易于维护,许多开发者会选择成熟的 ORM(对象关系映射)框架,SqlSugar 就是其中备受…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Linux --进程控制
本文从以下五个方面来初步认识进程控制: 目录 进程创建 进程终止 进程等待 进程替换 模拟实现一个微型shell 进程创建 在Linux系统中我们可以在一个进程使用系统调用fork()来创建子进程,创建出来的进程就是子进程,原来的进程为父进程。…...

搭建DNS域名解析服务器(正向解析资源文件)
正向解析资源文件 1)准备工作 服务端及客户端都关闭安全软件 [rootlocalhost ~]# systemctl stop firewalld [rootlocalhost ~]# setenforce 0 2)服务端安装软件:bind 1.配置yum源 [rootlocalhost ~]# cat /etc/yum.repos.d/base.repo [Base…...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...

VUE3 ref 和 useTemplateRef
使用ref来绑定和获取 页面 <headerNav ref"headerNavRef"></headerNav><div click"showRef" ref"buttonRef">refbutton</div>使用ref方法const后面的命名需要跟页面的ref值一样 const buttonRef ref(buttonRef) cons…...
