AcWing数据结构 - 数据结构在算法比赛中的应用(下)
目录
Trie树
Trie字符串统计
最大异或对
并查集
合并集合
连通块中点的数量
食物链
堆
堆排序
模拟堆
哈希表
模拟散列表
字符串哈希
Trie树
Trie字符串统计

思路:
设 idx索引用于构建树, 结点son[节点位置][节点分支指针],cnt[]记录单词个数
#include <iostream>using namespace std;const int N = 100010;int son[N][26], cnt[N], idx; //因为只包含小写字母,所以每个节点最多有26个子节点
char str[N];void insert(char *str)
{int p = 0; //下标是0的点即是根节点,又是空节点,如son[0][0]为根节点的分支'a'for (int i = 0; str[i]; i ++ ) //字符串末尾有'\0'{int u = str[i] - 'a';if (!son[p][u]) son[p][u] = ++ idx;//idx索引确定根位置p = son[p][u];}cnt[p] ++ ; //记录这个单词
}int query(char *str)
{int p = 0;for (int i = 0; str[i]; i ++ ){int u = str[i] - 'a';if (!son[p][u]) return 0;p = son[p][u];}return cnt[p];
}int main()
{int n;scanf("%d", &n);while (n -- ){char op[2];scanf("%s%s", op, str);if (*op == 'I') insert(str);else printf("%d\n", query(str));}return 0;
}
最大异或对
思路:
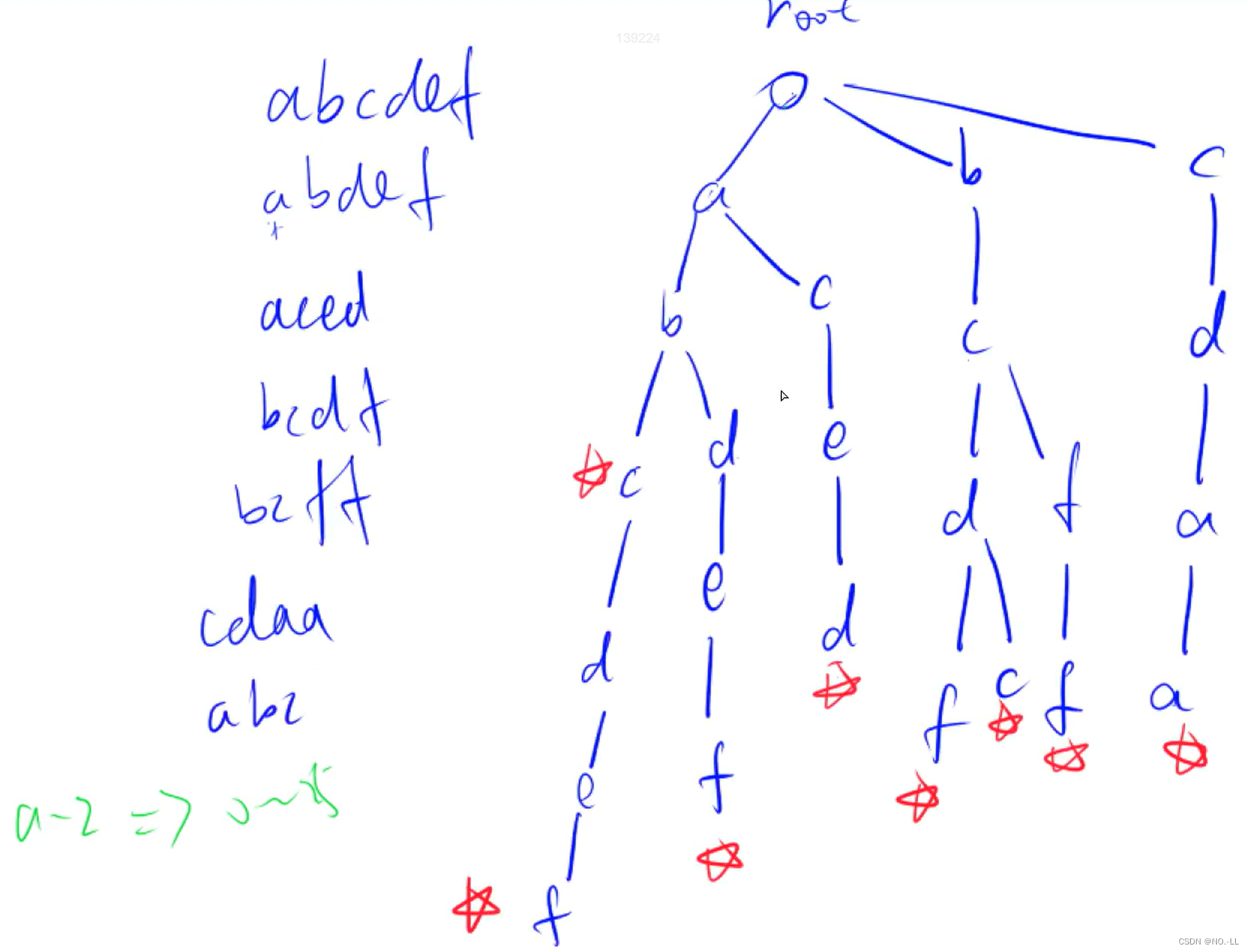
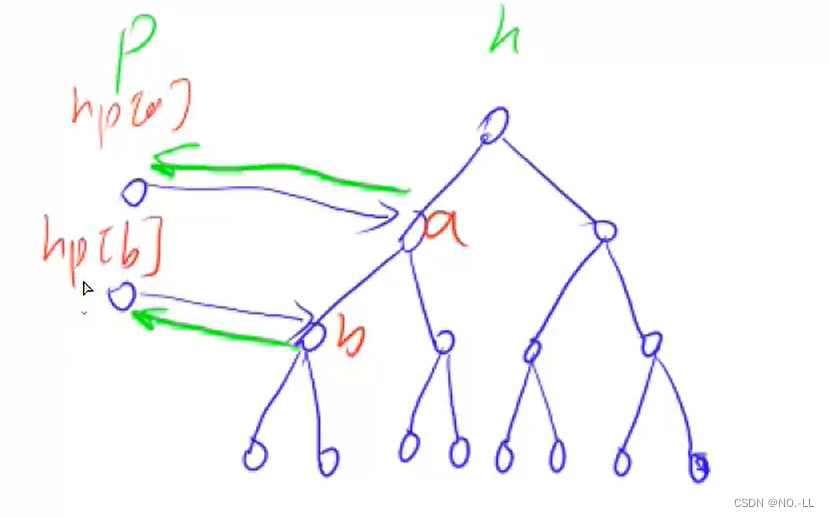
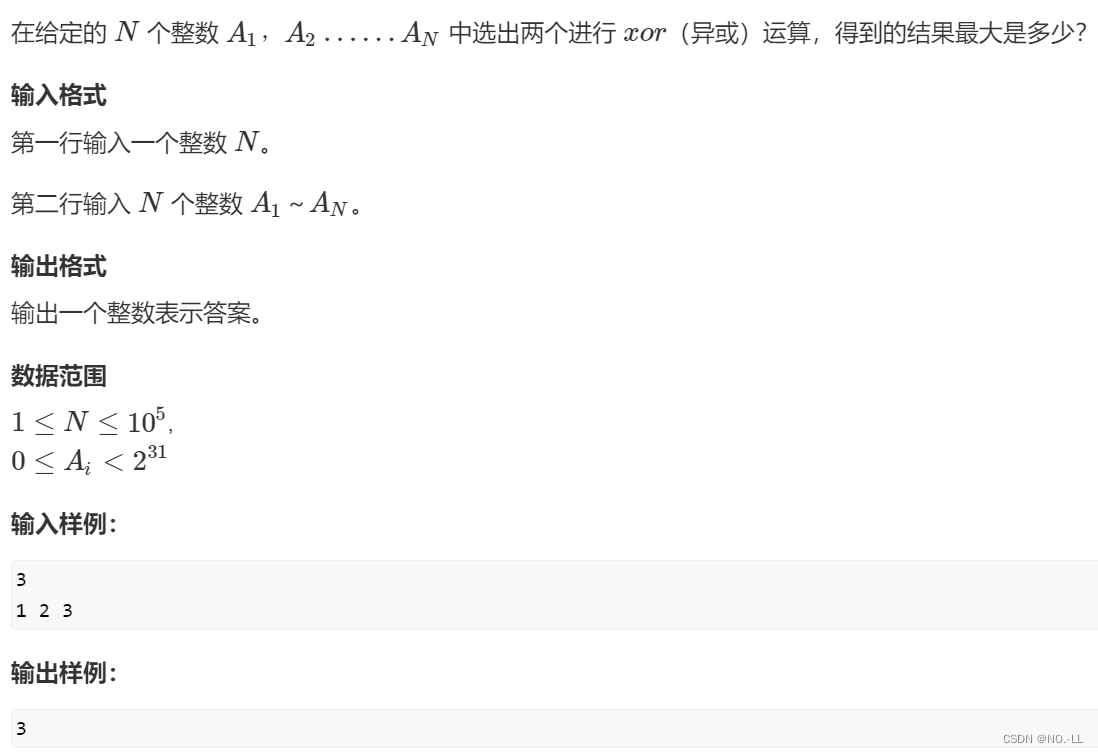
字典树不单单可以高效存储和查找字符串集合,还可以存储二进制数字:将每个数以二进制方式存入字典树,找的时候从最高位去找有无该位的异.
取x的第i位二进制数作为结点
~i 等价于 i>=0; 因为-1二进制全为1,取反为0,刚好结束
#include <iostream>
#include <algorithm>
using namespace std;int const N=100010,M=31*N; //M表示trie树的结点个数,即:31个二进制长度*总数int n,idx;
int a[N];
int son[M][2]; //因为只需要存二进制1和0,所以2即可void insert(int x)
{int p=0;for(int i=30;i>=0;i--){int u=x>>i&1; //取x的第i位二进制数是什么if(!son[p][u]) son[p][u]=++idx;p=son[p][u];}
}int search(int x)
{int p=0,res=0;for(int i=30;i>=0;i--) //遍历31个二进制位{int u=x>>i&1;if(son[p][!u]) //为了取异或后最大值,如果有不同的就先走{p=son[p][!u];res=res*2+1; //异或相异为1,res整体向前挪一位+1}else{p=son[p][u];res=res*2+0; //相同为0}}return res;
}int main()
{cin>>n;for(int i=0;i<n;i++){cin>>a[i];insert(a[i]);}int res=0;for(int i=0;i<n;i++){res=max(res,search(a[i]));}cout<<res<<endl;return 0;
}并查集
合并集合

思路:
路径压缩具体操作:
如图
find(1) p[1] = 2 p[1] = find(2)
find(2) p[2] = 3 p[2] = find(3)
find(3) p[3] = 4 p[3] = find(4)
find(4) p[4] = 4 将p[4]返回于是一路回溯;4=p[4]=p[3]=p[2]=p[1];

#include<iostream>
using namespace std;int p[100010];int find(int x)
{if(p[x]!=x) p[x]=find(p[x]);return p[x];
}int main()
{int n,m;cin>>n>>m;for(int i=1;i<=n;i++) p[i]=i;while(m--){char op;int a,b;cin>>op>>a>>b;if(op=='M') p[find(a)]=find(b); //将a的根插到b的根下,成为b分支else {if(find(a)==find(b))printf("Yes\n");elseprintf("No\n");}}return 0;
}
连通块中点的数量

算法 - 并查集详解:
算法 - 蓝桥杯并查集题型_小黄同学LL的博客-CSDN博客
#include<iostream>
using namespace std;
int n,m;
int p[100010],cnt[100010];
int find(int x)
{if(p[x]!=x) p[x]=find(p[x]);return p[x];
}int main()
{cin>>n>>m;for(int i=1;i<=n;i++){p[i]=i;cnt[i]=1;}while(m--){int a,b;string s;cin>>s;if(s=="C"){cin>>a>>b;a=find(a),b=find(b);p[a]=b;if(a!=b) cnt[b]+=cnt[a];}else if(s=="Q1"){cin>>a>>b;a=find(a),b=find(b);if(a==b) puts("Yes");else puts("No");}else{cin>>a;cout<<cnt[find(a)]<<endl;}}return 0;
}食物链

思路

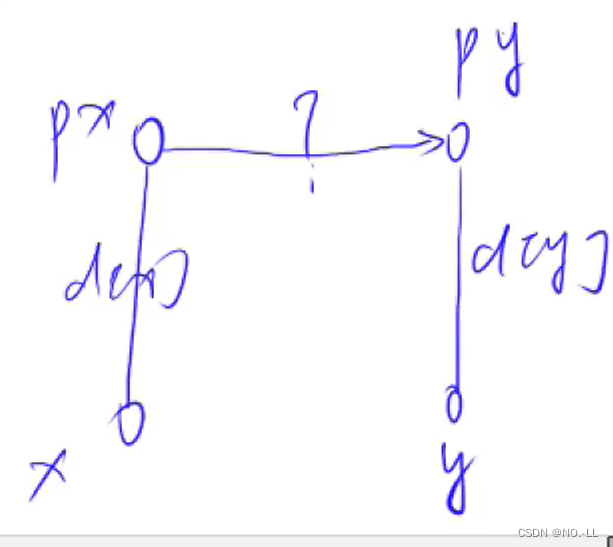
如果不是同一颗树,就把x树插到y树下,成为分支;由前面的合并操作,我们已经算出x到根px的距离d[x],y到根py的距离d[y];那么如何算px到py的距离呢?
我们设距离为 ?;
由于需要满足是同一种类,即最终的x到根距离%3==y到根距离%3
公式为(d[x]+?)%3==(d[y])%3;
简化得 ?=d[y]-d[x];
else if (px != py) //如果是不同的树 {p[px] = py; //把x树插到y树下,成为分支d[px] = d[y] - d[x]; // }
#include <iostream>using namespace std;const int N = 50010;int n, m;
int p[N], d[N];int find(int x)
{if (p[x] != x){int t = find(p[x]);d[x] += d[p[x]]; //d[p[x]]就指p[x]到上一个节点的距离,最终d[x]为该节点到宗结点距离p[x] = t;}return p[x];
}int main()
{scanf("%d%d", &n, &m);for (int i = 1; i <= n; i ++ ) p[i] = i; //有n种动物int res = 0;while (m -- ){int t, x, y;scanf("%d%d%d", &t, &x, &y);if (x > n || y > n) res ++ ; //大于范围,直接假else{int px = find(x), py = find(y); //找x和y的根节点if (t == 1) //判断同类,顺手记录{if (px == py && (d[x] - d[y]) % 3) res ++ ; //x和y在同一颗树上,//两个值到根节点的距离%3不同,说明不是同一类else if (px != py) //如果是不同的树{p[px] = py; //把x树插到y树下,成为分支d[px] = d[y] - d[x]; //根px到根py的距离}}else //判断是否x吃y{if (px == py && (d[x] - d[y] - 1) % 3) res ++ ;//x和y在同一颗树上,//x值到根节点的距离没有比y距离多1,说明吃不掉else if (px != py){p[px] = py;d[px] = d[y] + 1 - d[x]; //同理 }}}}printf("%d\n", res);return 0;
}堆
堆排序

思路:
1、向上调整算法:
void up(int u)
{while(u/2&&h[u/2]>h[u]){swap(h[u/2],h[u]);u/=2;}
}
2、向下调整算法 :
void down(int u)
{int t = u;if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;if (u != t){swap(h[u], h[t]);down(t);}
}如何手写一个堆?完全二叉树 5个操作
- 插入一个数 heap[ ++ size] = x; up(size);
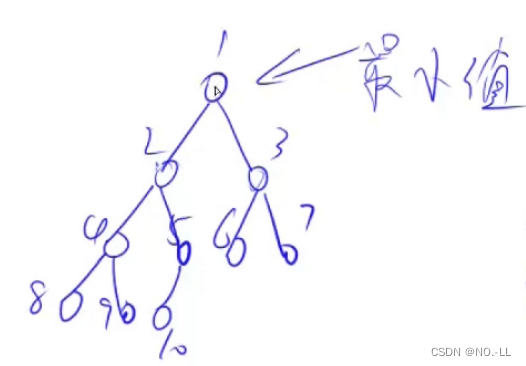
- 求集合中的最小值 heap[1]
- 删除最小值 heap[1] = heap[size]; size -- ;down(1);
- 删除任意一个元素 heap[k] = heap[size]; size -- ;up(k); down(k);
- 修改任意一个元素 heap[k] = x; up(k); down(k);
h[i] 表示第i个结点存储的值,i从1开始,2*i是左子节点,2*i + 1是右子节点
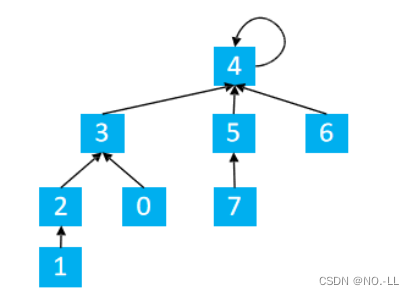
size 既表示堆里存储的元素个数,又表示最后一个结点的下标i为什么从n/2开始down?
因为n是最大值,n/2是n的父节点,因为n是最大,所以n/2是最大的有子节点的父节点,所以从n/2往前遍历,就可以把整个数组的父节点遍历一遍
如图,我们找到最大父节点5,然后向上遍历4321都是父节点,而5就是n/2
#include <iostream>
using namespace std;
int const N = 100010;int h[N], siz; //堆有两个变量h[N],size; 怎么这里的size和文件里有冲突,只能改成siz了void down(int u)
{int t = u;//t存储三个结点中存在的最小的结点的下标,初始化为当前结点uif (u * 2 <= siz && h[u * 2] < h[t]) t = u * 2; // 左子节点存在并且小于当前结点,更新t的下标if (u * 2 + 1 <= siz && h[u * 2 + 1] < h[t]) t = u * 2 + 1;//右子节点存在并且小于当前结点,更新t的下标if (t != u)//如果t==u意味着不用变动,u就是三个结点中拥有最小值的结点下标,否则交换数值{swap(h[t], h[u]);down(t); //交换数值后,t这个结点存储原本u的值,u存储存储t的值(三个数中的最小值)。u不用调整了,但t情况不明,可能需要调整。直到它比左右子节点都小}
}int main()
{int n, m;cin >> n >> m;for (int i = 1; i <= n; i ++ ) scanf("%d", &h[i]); siz = n; //初始化size,表示堆里有n 个元素for (int i = n / 2; i; i --) down(i); //把堆初始化成小根堆,从二叉树的倒数第二行开始,把数字大的下沉while (m -- ){printf("%d ", h[1]);h[1] = h[siz];siz --;down(1);}return 0;
}模拟堆

思路:
操作与堆排序一样,但由于需要插入和删除第k个数,要用额外数组作为指针存储位置,以便快速找到k,于是交换位置的同时也要交换指针
因为需要插入和删除第k个数,所以需要用hp[]记录idx值,然后用ph[]记录hp[]对应的结点
理解hp与ph数组,以及为什么需要它们
- 堆h[i]只能存放数据,不能存放是第几个数字,所以需要ph[k] = i来指明,第k个数字在h[]中对应的i是多少
- 在执行交换操作的时候,可以直接交换数字,swap(h[a],h[b])
- 但是对于ph[k_1] = a和ph[k_2] = b来说,a和b是它们存放的值,不 能通过值来找下标,也就是找不k_1,k_2是多少
- 于是引入hp[a] = k_2,hp[b] = k_2,则可以实现反向的操作
例如:
h[a] = 10, h[b] = 20 swap: h[a] = 20,h [b] = 10
hp[a] = 1 ,hp[b] = 2 swap:hp[a] = 2 ,hp[b] = 1
ph[1] = a ,ph[2] = b swap:ph[1] = b ,ph[2] = a
#include <iostream>
#include <algorithm>
#include <string.h>using namespace std;const int N = 100010;int h[N], ph[N], hp[N], cnt;void heap_swap(int a, int b)
{swap(ph[hp[a]],ph[hp[b]]);swap(hp[a], hp[b]);swap(h[a], h[b]);
}void down(int u)
{int t = u;if (u * 2 <= cnt && h[u * 2] < h[t]) t = u * 2;if (u * 2 + 1 <= cnt && h[u * 2 + 1] < h[t]) t = u * 2 + 1;if (u != t){heap_swap(u, t);down(t);}
}void up(int u)
{while (u / 2 && h[u] < h[u / 2]){heap_swap(u, u / 2);u >>= 1;}
}int main()
{int n, m = 0;scanf("%d", &n);while (n -- ){char op[5];int k, x;scanf("%s", op);if (!strcmp(op, "I")){scanf("%d", &x);cnt ++ ;m ++ ;ph[m] = cnt, hp[cnt] = m;h[cnt] = x;up(cnt);}else if (!strcmp(op, "PM")) printf("%d\n", h[1]);else if (!strcmp(op, "DM")){heap_swap(1, cnt);cnt -- ;down(1);}else if (!strcmp(op, "D")){scanf("%d", &k);k = ph[k];heap_swap(k, cnt);cnt -- ;up(k);down(k);}else{scanf("%d%d", &k, &x);k = ph[k];h[k] = x;up(k);down(k);}}return 0;
}哈希表
模拟散列表

算法 - 哈希表_NO.-LL的博客-CSDN博客
拉链法:
//拉链法
#include <iostream>
#include <cstring>
using namespace std;
const int N = 100003;//取大于1e5的第一个质数
int h[N],e[N],ne[N],idx;//开一个h槽,邻接表,h[]表示每个链表头节点,e[]表示x值,ne[]下一个节点下标
int n;
void insert(int x)
{int k = (x % N + N) % N;//c++中如果是负数,那他取模也是负的,加N再%N就一定是一个正数e[idx] = x;ne[idx] = h[k]; //相当于创建单链表h[k] = idx++;
}
bool find(int x)
{int k = (x % N + N) % N;for(int i = h[k];i != -1;i = ne[i]) //遍历链表{if(e[i] == x) return true;}return false;
}
int main()
{cin >> n;memset(h,-1,sizeof h);//先将槽清空,用-1表示while(n--){string op;int x;cin >> op >> x;if(op == "I"){insert(x);}else{if(find(x)){puts("Yes");}else{puts("No");}}}return 0;
}开放选址法
#include <cstring>
#include <iostream>
using namespace std;const int N=1e6+9; //开放寻址法一般开 数据范围的 2~3倍, 这样大概率就没有冲突了(我开了10倍)//开成质数取模时减小冲突概率
const int null=0x3f3f3f3f; //比1e9大的数(在数据范围找不到的数)
int h[N],n;int find(int x)
{int t=(x%N+N)%N; //将负值映射成正数while(h[t]!=null&&h[t]!=x) //如果位置不空并且不是x(不是自己){t++; //就找下一个位置if(t==N) t=0; //找到最后一个时再从0开找}return t; //如果这个位置是空的, 则返回的是他应该存储的位置
}
int main()
{cin>>n;memset(h,0x3f,sizeof h); //将每个值变为0x3f3f3f3f(以字节赋值 int4字节)while(n--){string op;int x;cin>>op>>x;if(op=="I"){h[find(x)]=x;}else{if(h[find(x)]==null) puts("No");else puts("Yes");}}return 0;
}字符串哈希

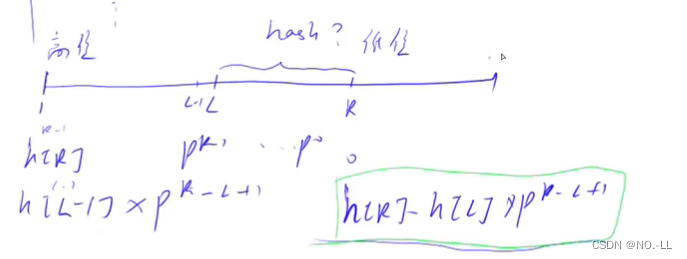
设 h[i]前i个字符的hash值;
为什么是h[l-1]? 由题意得,在abcdef中2 4为bcd,那么就是h[4]-h[2-1];
为什么是P^(r-l+1)? ABCDE 与 ABC 的前三个字符值是一样,只差两位,乘上 P^2 把 ABC 变为 ABC00,再用 ABCDE - ABC00 得到 DE 的哈希值。而P^2==p[3]==p[r-l+1](p从0次幂开始)如:ABCDE 的2 4为 BCD,就是ABCD-A000,即h[4]-h[1]*P^3;公式为h[4]-h[2-1]*P^(4-2+1)
#include<iostream>
using namespace std;typedef unsigned long long ull;
const int N=1e5+10,P=131; //或者P=13331
ull h[N],p[N]; //非常刚好的免去了取模的操作ull find(int l,int r)
{return h[r]-h[l-1]*p[r-l+1]; //部分求和
}int main()
{int n,m;cin>>n>>m;string x;cin>>x;p[0]=1; //p^0==1h[0]=0; //hash表从1开始有值,处理边界for(int i=0;i<n;i++){p[i+1]=p[i]*P;h[i+1]=h[i]*P+x[i]; //前缀和}while(m--){int l1,r1,l2,r2;cin>>l1>>r1>>l2>>r2;if(find(l1,r1)==find(l2,r2)) puts("Yes");else puts("No");}return 0;
}
相关文章:

AcWing数据结构 - 数据结构在算法比赛中的应用(下)
目录 Trie树 Trie字符串统计 最大异或对 并查集 合并集合 连通块中点的数量 食物链 堆 堆排序 模拟堆 哈希表 模拟散列表 字符串哈希 Trie树 Trie字符串统计 思路: 设 idx索引用于构建树, 结点son[节点位置][节点分支指针],cnt[]记录单…...
基于嵌入式libxml2的ARM64平台的移植(aarch64)
由于libxml在移植过程中依赖于zlib的库文件,因此本节内容包含zlib(V1.2.13)的移植libxml2(V2.10.3)的移植两部分组成。 (一)zlib的移植(基于arm64) 1、在github上下载zlib的最新源码压缩包&am…...
)
8. 字符串转换整数 (atoi)
题目描述 给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。 如果反转后整数超过 32 位的有符号整数的范围 [−231, 231 − 1] ,就返回 0。 假设环境不允许存储 64 位整数(有符号或无符号)。 示例 1&#x…...
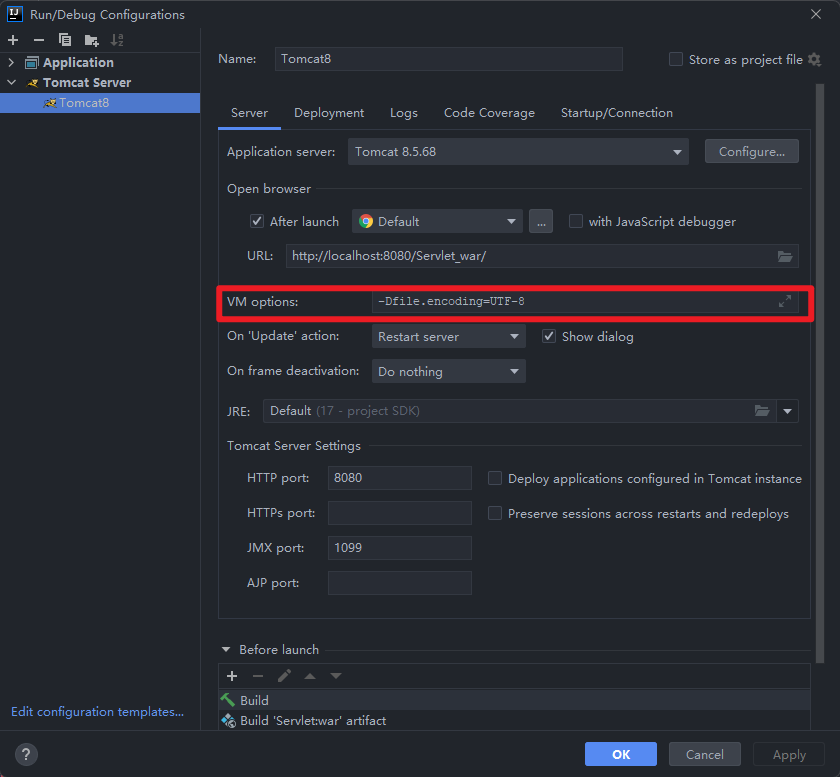
[Tomcat]解决IDEA中的Tomcat中文乱码问题
目录 1、IDEA 2、VM options 3、IDEA启动程序的存放目录 4、Tomcat 写在前面:此方法亲测有效!!! 1、IDEA 2、VM options 加上这两行: -Dfile.encodingUTF-8 -Dconsole.encodingUTF-8 3、IDEA启动程序的存放目录…...

python之dataclasses
一、场景 dataclasses模块提供了一种方便的方法来创建和管理数据对象 它可以帮助开发者更容易地创建简单的类,同时提供了一些实用的功能,例如自动实现__init__()、repr()、eq()等方法。 数据容器:如果您需要一个简单的类来存储一些数据&…...

【MapGIS精品教程】007:MapGIS投影变换案例教程
MapGIS投影变换,包括创建坐标系、定义投影、单点投影、类投影、批量投影。 文章目录 一、创建坐标系1. 创建高斯平面坐标系2. 创建阿尔伯斯投影二、定义投影三、投影变换1. 单点投影2. 类投影3. 批量投影一、创建坐标系 在MagGIS数据库中,有个空间参考系的文件夹,内置了常见…...

list数据根据属性字段去重
/*** 根据照片名称去重*/fun duplicateRemoval(list: MutableList<MediaBean>): MutableList<MediaBean>? {val mediaBeanList: MutableSet<MediaBean> if (Build.VERSION.SDK_INT > Build.VERSION_CODES.N) {TreeSet(Comparator.comparing(MediaBean::f…...
)
java教程(2023-3-8)
第一章:HelloWorld 1.java语言介绍 public class MainTest {public static void main(String[] args) { //软件分为系统软件和应用软件 //人机交互方式: 图形化界面 命令行方式/*常用的DOS命令:1.切换盘符:盘符 :2.创建文件夹m…...
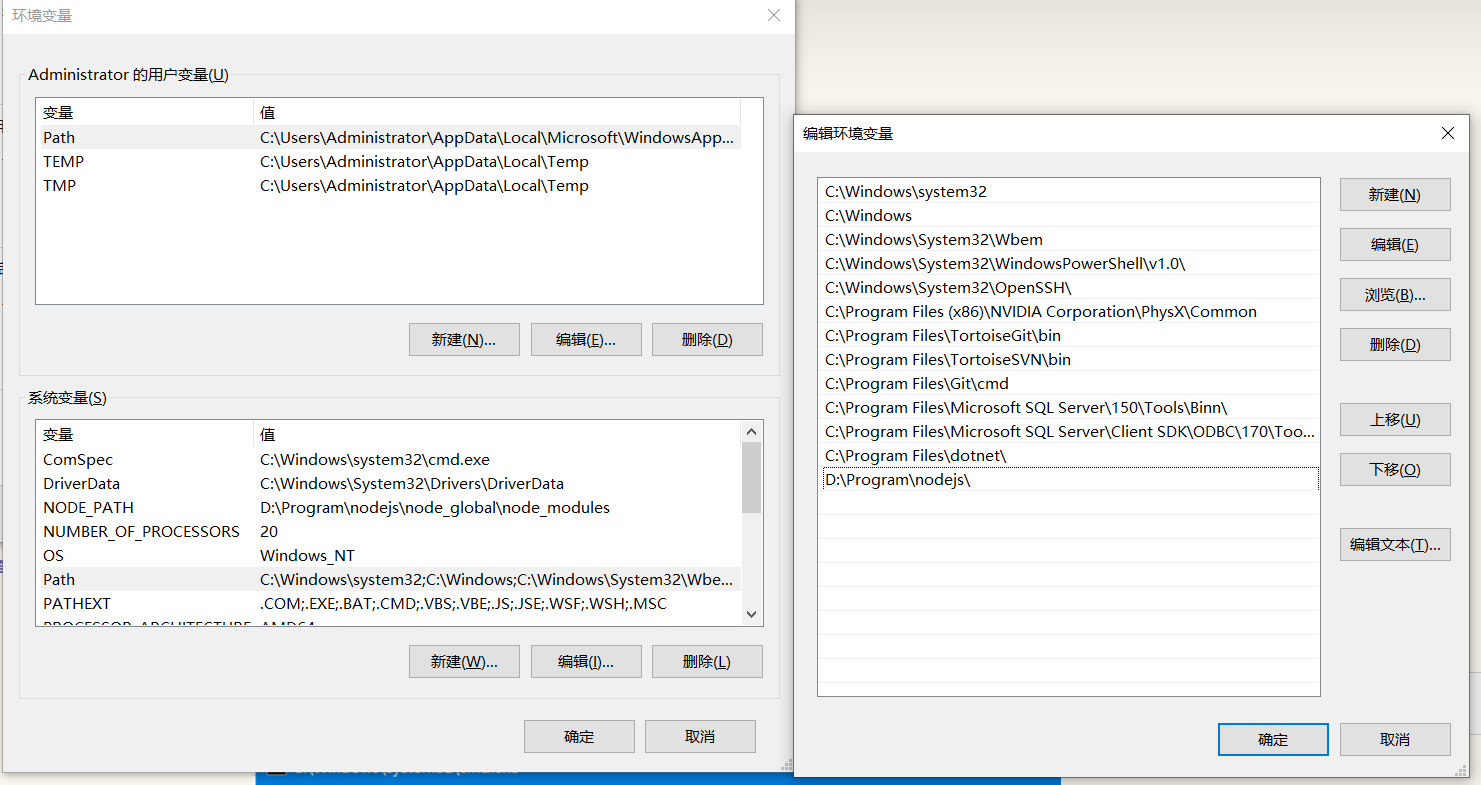
node 配置 vue npm配置
下载node 版本16https://nodejs.org/download/release/v16.16.0/node-v16.16.0-x64.msi复制安装地址,省空间,生报错老老实实复制就好D:\Program\nodejs新建node_cache和node_globalD:\Program\nodejs\node_cacheD:\Program\nodejs\node_global运行命令np…...

特斯拉、小鹏开路,城市NOA距好用还有几年?
作者 | Marshall 编辑 | 张祥威一项新技术,狂热的技术开发者往往会高估其发展速度,认为当下偶尔发生的安全问题,会随着数据积累和功能迭代被逐渐解决。 他们往往会说,“这个问题没有包含在我们的场景库中,但现在我们知…...

Vue 3第九章:WatchEffect高级侦听器
文章目录1. WatchEffect高级侦听器1.1. 使用 watchEffect 函数1.2. 停止侦听1.3. 侦听多个状态1.4. 懒执行总结1. WatchEffect高级侦听器 在 Vue 3 中,我们可以使用 watchEffect 函数来创建高级侦听器。与 watch 和 computed 不同,watchEffect 不需要指…...

c++基础——函数
函数的声明编程中的函数(function)一般是若干语句的集合。我们也可以将其称作“子过程(subroutine)”。在编程中,如果有一些重复的过程,我们可以将其提取出来,形成一个函数。函数可以接收若干值…...

DPDK系列之七DPDK中的虚拟化支持
一、DPDK和虚拟化 DPDK中大幅优化了网络通信的效率,这里也重点对网卡的虚拟化进行分析。在前面的文章中的学习可以判定网卡基本属于IO虚拟化。但是,虚拟化又有IO全虚拟化和IO半虚拟化之分,那么在DPDK中使用的哪种呢?IO虚拟化一般…...
-14)
设计模式~桥接模式(bridge)-14
目录 (1)优点: (2)缺点: (3)使用场景: (4)注意事项: (5)应用实例: 代码 桥接(Bridge)是用于把抽象化与实现化解耦,使得二者可以独立变化。这种类型的设计模式属于结构型模式&a…...

Java项目3 电子邮件
文章目录发电子邮件发电子邮件 RequestMapping("/sendmail")ResponseBodypublic String sendMail(Email email, HttpServletRequest request,HttpServletResponse response){HttpSession session request.getSession();SimpleMailMessage message new SimpleMailMe…...
-15)
设计模式~访问者模式(Visitor)-15
在访问者模式(Visitor Pattern)中,我们使用了一个访问者类,它改变了元素类的执行算法。通过这种方式,元素的执行算法可以随着访问者改变而改变。这种类型的设计模式属于行为型模式。根据模式,元素对象已接受…...

实战小项目之视频监控(1-1)
实战小项目之视频监控(1-1) 目前常见的视频监控和视频直播都是使用了 RTMP 和 RTSP 流媒体传输协议等。 RTSP(Real-Time Stream Protocol)由 Real Networks 和 Netscape 共同提出的,基于文本的多媒体播放 控制协议。…...
)
DEJA_VU3D - Cesium功能集 之 103-直角箭头(标绘+编辑)
前言 编写这个专栏主要目的是对工作之中基于Cesium实现过的功能进行整合,有自己琢磨实现的,也有参考其他大神后整理实现的,初步算了算现在有差不多实现小140个左右的功能,后续也会不断的追加,所以暂时打算一周2-3更的样子来更新本专栏(每篇博文都会奉上完整demo的源代码,…...
)
Vue 对象扩展运算符(…)
当编写一个方法时,我们允许它传入的参数是不确定的。这时候可以使用对象扩展运算符来作参数,看一个简单的列子: 1 2 3 4 5 6 7 8 function jspang(...arg){ console.log(arg[0]); console.log(arg[1]); console.log(arg[2]); …...

又是活动 没啥好说的 送代码
说明这里又一段代码:import time y 2.5 while y>-1.6:x -3.0while x<4.0:if (x*xy*y-1)**3<3.6*x*x*y*y*y or (x>-2.4 and x<-2.1 and y<1.5 and y>-1) or (((x<2.5 and x>2.2)or(x>3.4 and x<3.7)) and y>-1 and y<1.5) …...

智慧医疗能源事业线深度画像分析(上)
引言 医疗行业作为现代社会的关键基础设施,其能源消耗与环境影响正日益受到关注。随着全球"双碳"目标的推进和可持续发展理念的深入,智慧医疗能源事业线应运而生,致力于通过创新技术与管理方案,重构医疗领域的能源使用模式。这一事业线融合了能源管理、可持续发…...

模型参数、模型存储精度、参数与显存
模型参数量衡量单位 M:百万(Million) B:十亿(Billion) 1 B 1000 M 1B 1000M 1B1000M 参数存储精度 模型参数是固定的,但是一个参数所表示多少字节不一定,需要看这个参数以什么…...

Linux简单的操作
ls ls 查看当前目录 ll 查看详细内容 ls -a 查看所有的内容 ls --help 查看方法文档 pwd pwd 查看当前路径 cd cd 转路径 cd .. 转上一级路径 cd 名 转换路径 …...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

前端开发面试题总结-JavaScript篇(一)
文章目录 JavaScript高频问答一、作用域与闭包1.什么是闭包(Closure)?闭包有什么应用场景和潜在问题?2.解释 JavaScript 的作用域链(Scope Chain) 二、原型与继承3.原型链是什么?如何实现继承&a…...

Spring数据访问模块设计
前面我们已经完成了IoC和web模块的设计,聪明的码友立马就知道了,该到数据访问模块了,要不就这俩玩个6啊,查库势在必行,至此,它来了。 一、核心设计理念 1、痛点在哪 应用离不开数据(数据库、No…...

重启Eureka集群中的节点,对已经注册的服务有什么影响
先看答案,如果正确地操作,重启Eureka集群中的节点,对已经注册的服务影响非常小,甚至可以做到无感知。 但如果操作不当,可能会引发短暂的服务发现问题。 下面我们从Eureka的核心工作原理来详细分析这个问题。 Eureka的…...
集成 Mybatis-Plus 和 Mybatis-Plus-Join)
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join
纯 Java 项目(非 SpringBoot)集成 Mybatis-Plus 和 Mybatis-Plus-Join 1、依赖1.1、依赖版本1.2、pom.xml 2、代码2.1、SqlSession 构造器2.2、MybatisPlus代码生成器2.3、获取 config.yml 配置2.3.1、config.yml2.3.2、项目配置类 2.4、ftl 模板2.4.1、…...