实验7 图像水印
本次实验大部分素材来源于山大王成优老师的讲义以及冈萨雷斯(MATLAB版),仅作个人学习笔记使用,禁止用作商业目的。
文章目录
- 一、实验目的
- 二、实验例题
- 1. 数字图像水印技术
- 2. 可见水印的嵌入
- 3. 不可见脆弱水印
- 4. 不可见鲁棒水印
一、实验目的
- 了解数字图像水印技术的基本原理、分类和应用。
- 掌握简单的可见水印和不可见水印的嵌入方法。
- 实现一种基于 DCT 的不可见鲁棒水印,并进行水印鲁棒性测试。
二、实验例题
1. 数字图像水印技术
数字图像水印处理是把数据插入到一幅图像中的过程,以这样的方式对图像内容进行保护。一个典型的图像水印处理系统如图 1 所示。
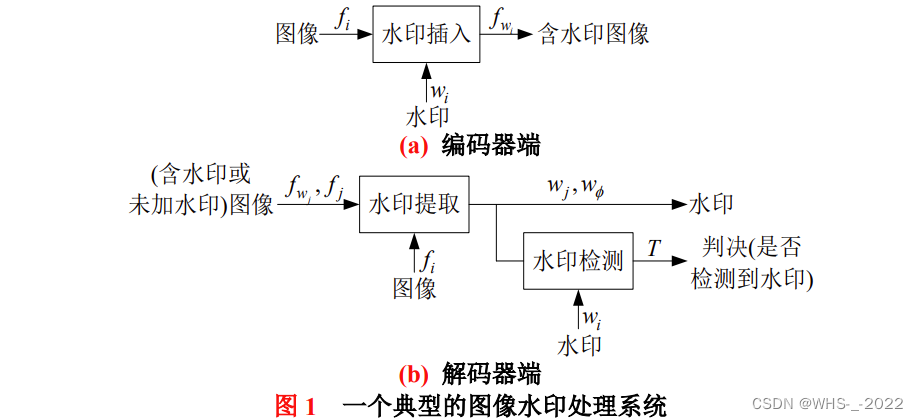
在编码器端,发送者将水印 wiw_iwi 嵌入到原始图像 fif_ifi
中,产生含水印图像 fwif_{w_i}fwi ;在解码器端,接收者提取和验证含水印图像 fwif_{w_i}fwi 或 未添加水印图像 fjf_jfj 中水印 wiw_iwi 的存在性。wjw_jwj 是提取的水印,T 是预定义的阈值。
根据不同的特性,数字水印可以从以下三个方面进行分类:
- 根据水印的鲁棒性,可以将水印分为鲁棒水印和脆弱水印。鲁棒水印是指含水印图像在经过各种处理操作甚至恶意攻击后,隐藏在其中的水印信息仍然可以被提取出来,主要用于版权保护;脆弱水印对图像的变化非常敏感,含水印图像发生变化后将影响水印的检测,从而提示图像已被修改,主要用于图像内容认证。
- 根据水印的可见性,可以将水印分为可见水印和不可见水印。可见水印是一幅不透明或半透明的子图像,它对观察者是可见的,电视网络通常将可见水印放在屏幕的左上角或右下角以证明它的版权归属;不可见水印裸眼是看不见的,但可以通过一个合适的水印提取方法从含水印图像中恢复出水印。
- 根据水印内容,水印又可分为无意义水印和有意义水印。无意义水印对应于一段伪随机序列,通常只能判断图像中是否存在水印,而无法直接观察;有意义水印是指水印本身也是一幅二值图像或者灰度图像,可以从含水印图像中提取并通过观察确认。
2. 可见水印的嵌入
可见水印一般通过与原始图像直接叠加的方式实现嵌入,如式(1)(1)(1)所示。水印图像 www 通过线性组合的方式嵌入到原始图像 fff 中,得到含水印图像 fwf_wfw 。
fw=(1−α)f+αw(1)f_{w}=(1-\alpha) f+\alpha w\tag1 fw=(1−α)f+αw(1)
3. 不可见脆弱水印
在像素深度为 8 位的图像中,最低有效位(Least Significant Bit, LSB)对图像的质量影响较小。利用这种特性可以在不影响原始图像主观质量的情况下,将水印图像插入到原始图像的最低几位有效位中。然而,这种基于 LSB 的水印嵌入法则对诸如 JPEG 压缩、空间滤波等常见的信号处理操作特别敏感,鲁棒性较差。
以图 2 所示的原始 Lena 图像和水印图像为例,式(2)(2)(2)给出了一种基于 LSB 的脆弱水印嵌入法则,将水印图像的两位最高有效位(Most Significant Bit, MSB)插入到了 Lena 图像的最低两位有效位中。
fw=4⌊f4⌋+⌊w64⌋(2)f_{w}=4\left\lfloor\frac{f}{4}\right\rfloor+\left\lfloor\frac{w}{64}\right\rfloor\tag2 fw=4⌊4f⌋+⌊64w⌋(2)
其中,f 为原始图像,w 为水印图像,f_w 为嵌入水印后的图像,⌊⋅⌋\lfloor\cdot\rfloor⌊⋅⌋ 为下取整操作(可用
MATLAB 函数 floor 来实现)。

使用 imwrite 函数进行 JPEG 压缩攻击测试:
A = imread('1.Lena 图像.tif');
imwrite(A, 'JPEG 压缩图像.jpg', 'quality', 80); %80 表示质量因子,其值越小,表示图
像被压缩的越厉害
D = imread('JPEG 压缩图像.jpg');
4. 不可见鲁棒水印
当前,常见的鲁棒水印算法都是在频域中实现水印嵌入的,以经典的基于离散余弦变换(Discrete Cosine Transform, DCT)的鲁棒水印算法为例,主要过程如下:
- 对原始图像进行二维 DCT 变换,DCT 变换具有较好的能量集中特性,可以将
低频能量集中在图像的左上角:
A = imread('3.Lena 图像.tif');
A = double(A);
A_dct = dct2(A); %二维 DCT 变换,A_dct 为得到的 DCT 系数矩阵
A1 = idct2(A_dct); %二维逆 DCT 变换
A1 = uint8(A1);
figure, imshow(A1) %重建图像
- 一般来说,选取的 DCT 系数越大,水印嵌入对图像的影响就越小。为减少水印嵌入对图像的影响,从 DCT 系数矩阵中选取幅值较大的系数进行水印嵌入。
思路:可先将所有 DCT 系数变为一维行向量,然后按照幅值进行降序排序(sort 函数),选取排列靠前的 DCT 系数作为水印的具体嵌入位置。
- 长度为 k 的伪随机序列
w1,w2,⋯,wkw_{1}, w_{2}, \cdots, w_{k}w1,w2,⋯,wk作为无意义水印通过式(3)(3)(3)嵌入原始图像,其中,cic_ici 为选取的 DCT 系数,ci′c'_ici′ 为经过水印调整后的系数,α\alphaα 为嵌入强度。
ci′=ci(1+αwi),1≤i≤k(3)c_{i}^{\prime}=c_{i}\left(1+\alpha w_{i}\right), \quad 1 \leq i \leq k \tag3 ci′=ci(1+αwi),1≤i≤k(3)
伪随机数序列类似于随机数序列,但它可以通过设置初始状态,来保证每次得到的随机数是相同的:
randn('seed', 0); %选定伪随机序列发生器“seed”和初始状态 0
K = randn(1, 1000); %产生长度为 1000 的伪随机数序列 K
- 在水印提取时,首先得到嵌入水印的 k 个 DCT 系数,然后通过式(4)(4)(4)完成水印的恢复:
w^i=c^i−ciαci,1≤i≤k(4)\hat{w}_{i}=\frac{\hat{c}_{i}-c_{i}}{\alpha c_{i}}, \quad 1 \leq i \leq k\tag4w^i=αcic^i−ci,1≤i≤k(4)
the c^i\hat{c}_ic^i will be approximations of the ci′c_{i}^{\prime}ci′.
- 使用式(5)(5)(5)给出的相关系数表达式,对提取的水印与原始水印的相关性进行评价,相关系数 γγγ 在 0 到 1 之间,其值越大,表示两者间的相关性越好,水印的损失也就越小。通过比较 γγγ 与预设定的阈值 TTT 可以判断一幅图像是否存在水印,详见教材 P397 式(8.73)(8.73)(8.73)。
γ=∑i=1k(w^i−w^‾)(wi−wˉ)∑i=1k(w^i−w^‾)2∑i=1k(wi−wˉ)2,1≤i≤k(5)\gamma=\frac{\sum_{i=1}^{k}\left(\hat{w}_{i}-\overline{\hat{w}}\right)\left(w_{i}-\bar{w}\right)}{\sqrt{\sum_{i=1}^{k}\left(\hat{w}_{i}-\overline{\hat{w}}\right)^{2} \sum_{i=1}^{k}\left(w_{i}-\bar{w}\right)^{2}}}, \quad 1 \leq i \leq k\tag5 γ=∑i=1k(w^i−w^)2∑i=1k(wi−wˉ)2∑i=1k(w^i−w^)(wi−wˉ),1≤i≤k(5)
若图像遭到恶意攻击,水印信息会受到损坏,提取水印与原始水印的相关系数也会下降,而下降越小的水印算法其对各种攻击的鲁棒性就越强。
相关文章:

实验7 图像水印
本次实验大部分素材来源于山大王成优老师的讲义以及冈萨雷斯(MATLAB版),仅作个人学习笔记使用,禁止用作商业目的。 文章目录一、实验目的二、实验例题1. 数字图像水印技术2. 可见水印的嵌入3. 不可见脆弱水印4. 不可见鲁棒水印一、…...

如何实现大文件断点续传、秒传
大家先来了解一下几个概念: 「文件分块」:将大文件拆分成小文件,将小文件上传\下载,最后再将小文件组装成大文件; 「断点续传」:在文件分块的基础上,将每个小文件采用单独的线程进行上传\下载&…...

备战蓝桥python——完全平方数
完全平方数 链接: 完全平方数 暴力解法: n int(input()) for i in range(1, n1):if(((i*n)**0.5)%10.0):print(i)break运用数论相关知识求解 任意一个正整数都可以被分解成若干个质数乘积的形式,例如 :2022∗5120 \ 2^{2}*5^{1}\,20 22∗51 由此…...
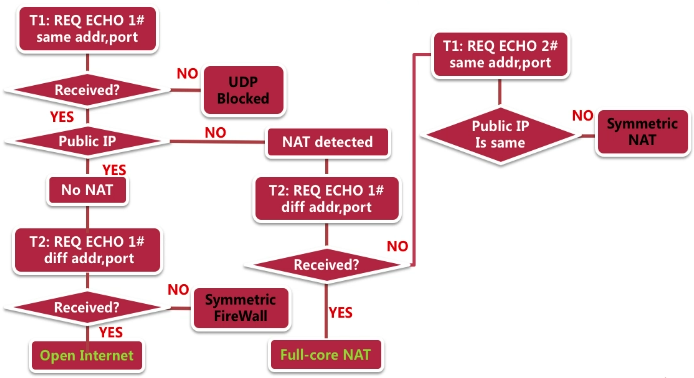
WebRTC中的NAT穿透
NAT简介 我们知道,WebRTC会按照内网、P2P、中转的顺序来尝试连接。在大部分的情况下,实际是使用P2P或者中转的。这里P2P的场景主要使用的技术就是NAT穿透。 我们先简单了解下NAT。NAT在真实网络中是常见的,它的出现一是为了解决ipv4地址不够…...
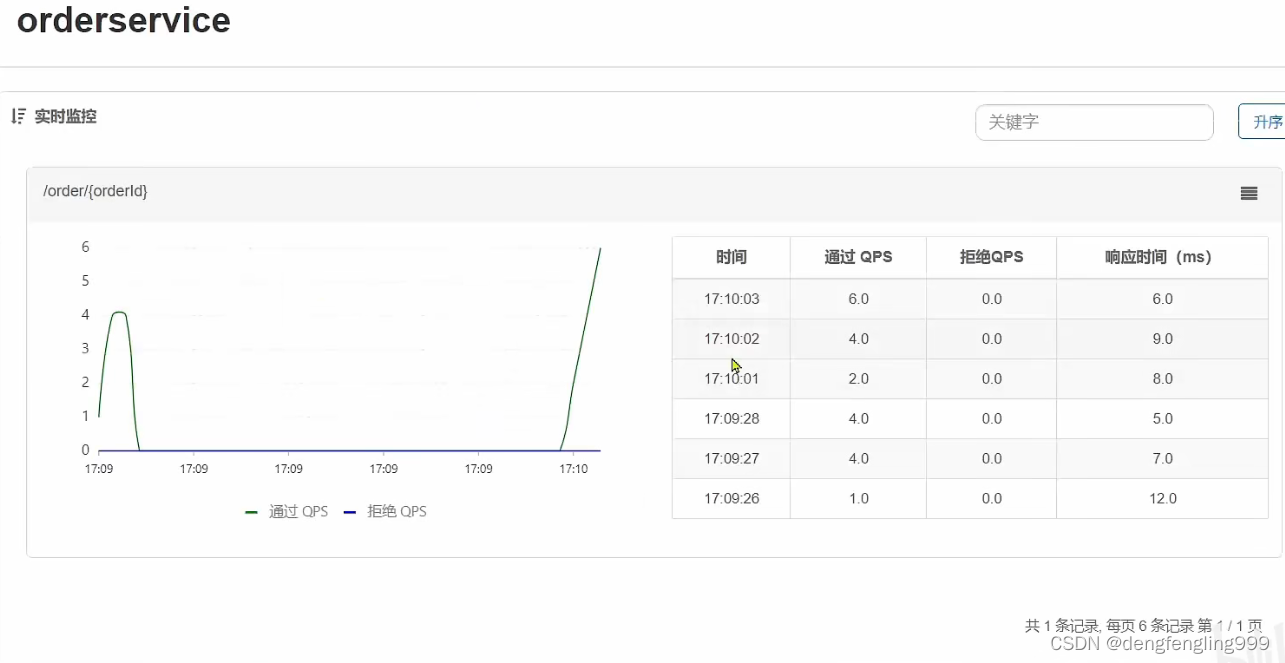
SpringCloud-高级篇(一)
目录: (1)初识Sentinel-雪崩问题的解决方案 (2)服务保护Sentinel和Hystrix对比 (3)Sentinel初始-安转控制台 (4)整合微服务和Sentinel 微服务高级篇 (1&…...
电脑自动重启是什么原因?详细解说
案例:电脑自动重启是什么原因? “一台用了一年的电脑,最近使用,每天都会一两次莫名其妙自动重启,看了电脑错误日志,看不懂什么意思,一直找不到答案。有没有高手知道怎么解决这个问题的。” 当…...

2023美国大学生数学建模竞赛E题思路
problem 背景: 光污染用于描述过度或不良使用人造光。我们称之为光污染的一些现象包括光侵入、过度照明和光杂波。在大城市,太阳落山后,这些现象最容易在天空中看到:然而,它们也可能发生在更偏远的地区。 光污染会改变我们对夜空…...

蓝桥杯三月刷题 第五天
文章目录💥前言😉解题报告💥数的分解🤔一、思路:😎二、代码:💥前言 上午没写,下午写了会被朋友拉出去耍,被冷风吹到了,而且被他坑了,根本没有玩骑…...
Echarts 水波图实现
开发的项目中需要实现这样一个水波图,例如下图在echarts官网中找了很久没找到,后面是在Echarts社区中找到的,实现了大部分的样式,但是还有一些数据的展示没有实现。水波图的数值展示是默认整数百分比,我的需求是需要保…...
逻辑优化基础-shannon decomposition
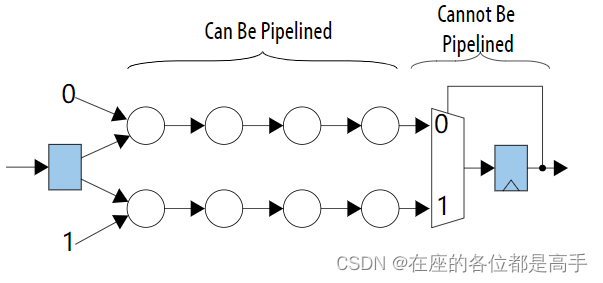
1. 简介 在逻辑综合中,香农分解(Shannon decomposition)是一种常用的布尔函数分解方法。它将一个布尔函数分解为两个子函数的和,其中每个子函数包含一个布尔变量的取反和非取反的部分。 具体来说,假设对于一个布尔函…...

Java中线程池的创建与使用
前言:默认线程池的弊端在线程池应用中,参考阿里巴巴java开发规范:线程池不允许使用Executors去创建,不允许使用系统默认的线程池,推荐通过ThreadPoolExecutor的方式,这样的处理方式让开发的工程师更加明确&…...

关于HashMap与OkHttp的使用
写了一个okhttp的post请求方法,添加参数很麻烦,需要封装: //post请求public static void sendOkHttpRequestPost(String address , Callback callback) {OkHttpClient client new OkHttpClient();// 创建表单参数RequestBodyRequestBody fo…...
【独家】)
华为OD机试 - 单词倒序(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:单词倒序…...
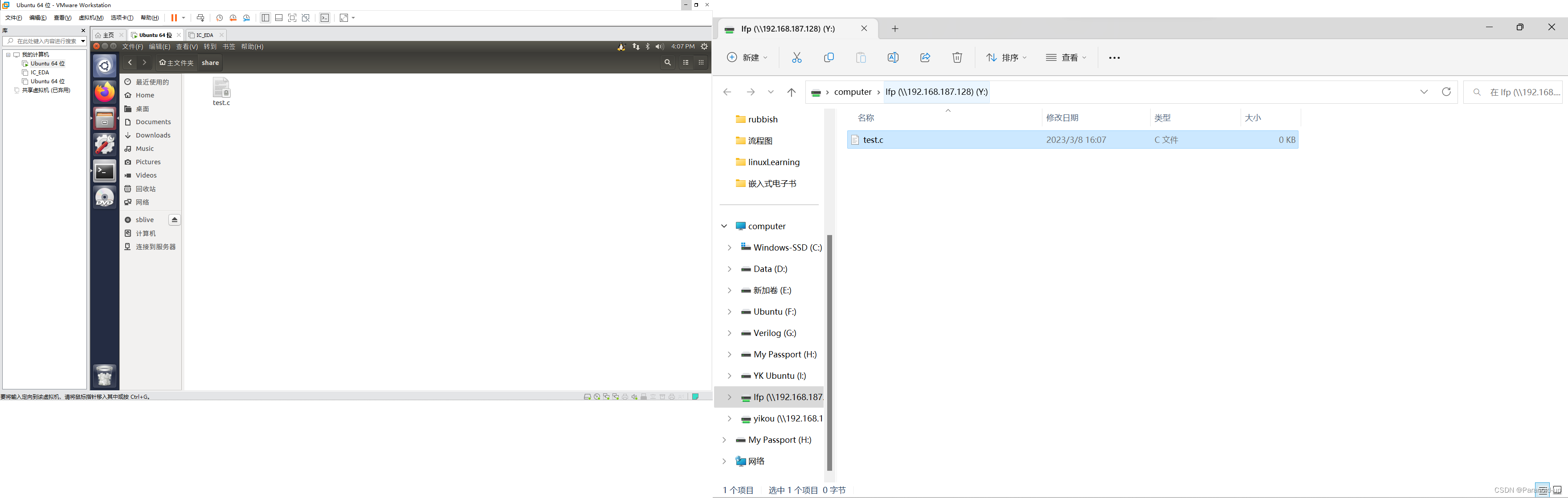
搭建Samba服务器
搭建Samba服务器 文章目录搭建Samba服务器samba安装安装命令配置-ubuntu侧为samba服务器创建一个共享目录share创建使用该共享文件夹的账号修改samba服务器配置文件重启samba服务windows创建映射1.点击映射网络驱动器2.输入Ubuntu中的ip地址及其用户信息3.输入用户信息及其密码…...
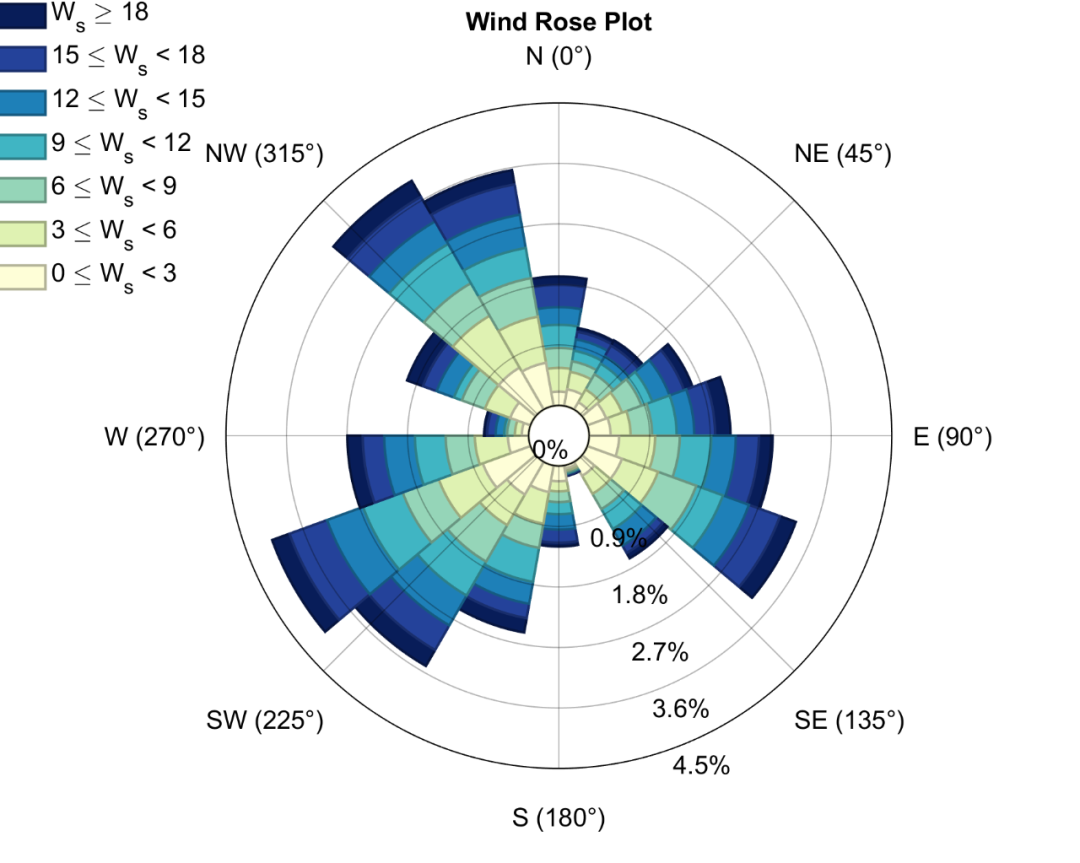
Matlab进阶绘图第5期—风玫瑰图(WindRose)
风玫瑰图(Wind rose diagram)是一种特殊的极坐标堆叠图/统计直方图,其能够直观地表示某个地区一段时期内风向、风速的发生频率。 风玫瑰图在建筑规划、环保、风力发电、消防、石油站设计、海洋气候分析等领域都有重要作用,所以在一些顶级期刊中也能够看…...
:数仓报表场景☞通过执行计划详解”行转列”,”列转行”是如何实现的)
【SQL开发实战技巧】系列(二十四):数仓报表场景☞通过执行计划详解”行转列”,”列转行”是如何实现的
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...
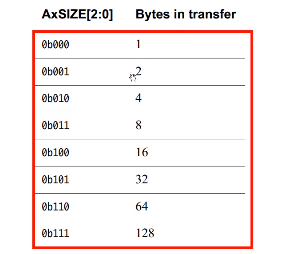
XILINX AXI总线学习
AXI介绍什么是AXI?AXI(高级可扩展接口),是ARM AMBA的一部分;AMBA:高级微控制器总线架构;是1996年首次引入的一组微控制器总线;开放的片内互联的总线标准,能在多主机设计中实现多个控…...

2022CCPC女生赛(补题)(A,C,E,G,H,I)
迟了好久的补题,,现在真想把当时赛时的我拉出来捶一拳排序大致按照题目难度。C. 测量学思路:直接循环遍历判断即可,注意角度要和2π取个最小值。AC Code:#include <bits/stdc.h>typedef long long ll; const int…...

【Nginx】Nginx的安装配置
环境说明系统:Centos 7一、编译安装Nginx官网下载地址nginx: download#安装依赖 [rootnginx nginx-1.22.1]# yum install gcc pcre pcre-devel zlib zlib-devel -y #从官网下载Nginx安装包,并进行解压、编译、安装 [rootnginx ~]# wget https://nginx.or…...

数学小课堂:统计时有效地筛选数据
文章目录引言I 被爆冷门的原因II 统计时有效地筛选数据2.1 统计数据的常见问题2.2 大数据的特征2.3 有效筛选数据的原则引言 在博弈论中很多结果有发生的概率,而概率这件事只是估计出来的,并不准确。因此,一旦加入博弈的选手多了之后&#x…...
)
Java 语言特性(面试系列2)
一、SQL 基础 1. 复杂查询 (1)连接查询(JOIN) 内连接(INNER JOIN):返回两表匹配的记录。 SELECT e.name, d.dept_name FROM employees e INNER JOIN departments d ON e.dept_id d.dept_id; 左…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题(可多选) 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘:专注于发现数据中…...

鱼香ros docker配置镜像报错:https://registry-1.docker.io/v2/
使用鱼香ros一件安装docker时的https://registry-1.docker.io/v2/问题 一键安装指令 wget http://fishros.com/install -O fishros && . fishros出现问题:docker pull 失败 网络不同,需要使用镜像源 按照如下步骤操作 sudo vi /etc/docker/dae…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
