知识蒸馏论文阅读:DKD算法笔记
标题:Decoupled Knowledge Distillation
会议:CVPR2022
论文地址:https://ieeexplore.ieee.org/document/9879819/
官方代码:https://github.com/megvii-research/mdistiller
作者单位:旷视科技、早稻田大学、清华大学
文章目录
- Abstract
- 1. Introduction
- 2. Related work
- 3. Rethinking Knowledge Distillation
- 3.1. Reformulating KD
- 3.2. Effects of TCKD and NCKD
- 3.3. Decoupled Knowledge Distillation
- 4. Experiments
- 4.1. Main Results
- 4.2. Extensions
- 5. Discussion and Conclusion
Abstract
SOTA的蒸馏方法主要基于蒸馏来自中间层的深度特征,而logit蒸馏的重要性被极大地忽略。为了给logit蒸馏的研究提供一个新的视角,我们将经典的KD损失重新表示为两部分,即目标类知识蒸馏(TCKD)和非目标类知识蒸馏(NCKD)。我们经验地研究并证明了这两部分的作用:TCKD迁移了关于训练样本的“难度”的知识,而NCKD则是logit蒸馏起作用的重要原因。更重要的是,我们揭示了经典的KD损失是一个耦合的形式,它①抑制了NCKD的有效性,②限制了平衡这两部分的灵活性。为了解决这些问题,我们提出了解耦知识蒸馏(Decoupled Knowledge Distillation,DKD),使得TCKD和NCKD能够更加高效灵活地发挥作用。与复杂的基于特征的方法相比,我们的DKD在用于图像分类和目标检测任务的CIFAR-100、ImageNet和MS-COCO数据集上取得了相当甚至更好的结果,并且具有更好的训练效率。本文证明了logit蒸馏的巨大潜力,希望对未来的研究有所帮助。
1. Introduction
在过去的几十年中,深度神经网络(DNN)给计算机视觉领域带来了革命性的变化,成功地促进了图像分类、目标检测和语义分割等各种真实场景任务。然而,强大的网络通常受益于较大的模型容量,引入了高昂的计算和存储成本。在工业应用中这种成本并不合适,因此轻量级模型被广泛部署。在过去的文献中,一个可能降低成本的方向是知识蒸馏(KD)。KD代表了一系列将知识从重型模型(教师)迁移到轻型模型(学生)的方法,可以在不引入额外成本的情况下提高轻模型的性能。
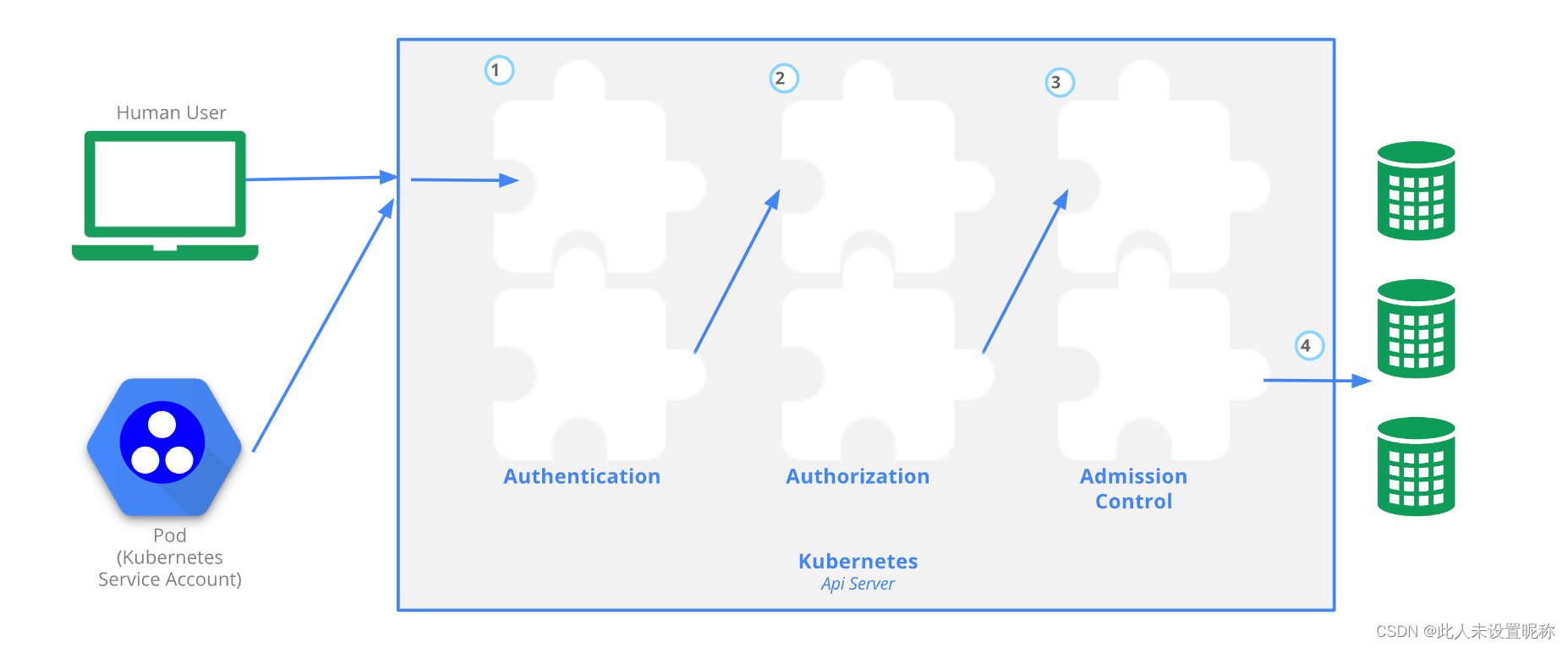
Hinton等人首次提出KD的概念,通过最小化教师和学生的预测logit之间的KL散度(KL-Divergence)来迁移知识(图1a)。自FitNets以来,大部分研究都关注从中间层的深度特征中蒸馏知识。与基于logit的方法相比,特征蒸馏在各种任务上的性能都更优越,因此对logit蒸馏的研究几乎没有触及。然而,基于特征的方法的训练成本并不令人满意,因为在训练过程中引入了额外的计算和存储使用(例如网络模块和复杂操作)来蒸馏深度特征。

logit蒸馏只需要微不足道的计算和存储成本,但性能较差。直觉上,logit蒸馏应该达到与特征蒸馏相当的性能,因为logit比深度特征具有更高的语义层次。我们猜想logit蒸馏的潜力受到未知原因的限制,导致性能不理想。为了重振基于logits的方法,我们通过研究KD的机制开始这项工作。首先,我们将分类预测分为两个层次:①对目标类和所有非目标类进行二分类预测;②对每个非目标类进行多分类预测。基于此,我们将经典的KD损失重新表示为两部分,如图1b所示。一部分是针对目标类的二分类logit蒸馏,另一部分针对是非目标类的多分类logit蒸馏。出于简化,我们分别将其命名为目标类知识蒸馏(TCKD)和非目标类知识蒸馏(NCKD)。这种重新表示使得我们可以独立地研究两部分的作用。
TCKD通过二分类logit蒸馏来迁移知识,即只提供目标类的预测,不知道每个非目标类的具体预测。一个合理的假设是TCKD迁移了关于训练样本“难度”的知识,即这些知识描述了识别每个训练样本的难易程度。为了验证这一点,我们从三个方面设计实验来增加训练数据的“难度”,即更强大的增广、更嘈杂的标签和内在地有挑战性的数据集。
NCKD只考虑非目标logits之间的知识。有趣的是,我们经验地证明了仅应用NCKD取得了与经典的KD相当甚至更好的结果,表明非目标logits中包含的知识至关重要,可能是重要的“暗知识”。
更重要的是,我们的重新表示表明,经典的KD损失是一个高度耦合的形式(如图1b所示),这可能是logit蒸馏潜力被限制的原因。首先,NCKD损失项通过一个与教师在目标类别上预测置信度负相关的系数来加权。因此较大的预测分数会导致较小的权重。这种耦合显著抑制了NCKD对预测良好的(well-predicted)训练样本的作用。这种抑制是不合适的,因为教师在训练样本中置信度越高,它所能提供的知识就越可靠和有价值。其次,TCKD和NCKD的重要性是耦合的,即不允许将TCKD和NCKD分别加权。这种限制也是不合适的,因为TCKD和NCKD的贡献来自不同的方面,应该分别考虑。
针对这些问题,我们提出了一种灵活高效的logit蒸馏方法,取名为解耦知识蒸馏(Decoupled Knowledge Distillation,DKD,图1b)。DKD将NCKD损失从与教师置信度负相关的系数解耦,将其替换为恒定值,提高了对预测良好的样本的蒸馏效果。同时,NCKD和TCKD也是解耦的,可以通过调整各部分的权重来分别考虑它们的重要性。
总的来说,我们的贡献概括如下:
- 我们通过将经典的KD分为TCKD和NCKD,为研究logit蒸馏提供了一个有洞察力的视角。此外,分别对两部分的作用进行了分析和证明。
- 我们揭示了经典的KD损失因其高度耦合形式而导致的局限性。NCKD与教师置信度的耦合抑制了知识迁移的有效性。TCKD与NCKD的耦合限制了平衡这两部分的灵活性。
- 为了克服这些局限性,我们提出了一种有效的logit蒸馏方法DKD。DKD在各种任务上取得了SOTA的性能。我们还通过实验验证了与基于特征的蒸馏方法相比,DKD具有更高的训练效率和更好的特征迁移能力。
2. Related work
知识蒸馏的概念最早由Hinton等人提出。KD定义了一种学习方式,即使用较大的教师网络来指导较小的学生网络进行许多任务的训练。“暗知识”通过来自教师的软标签迁移给学生。为了提高对负logits的关注,超参数温度被引入。后续的工作可以分为两类,从logits蒸馏和从中间特征蒸馏。
以往关于logit蒸馏的工作主要集中于提出有效的正则化和优化方法,而非新颖的方式。DML提出了一种相互学习的方式来同时训练学生和教师。TAKD引入了一个名为“助教”的中型网络来弥补教师和学生之间的差距。除此之外,一些工作也关注对经典KD方法的解读。
SOTA的方法主要基于中间特征,可以直接将表示从教师迁移给学生或者将教师中捕获的样本之间的相关性迁移给学生。大多数基于特征的方法都能取得更好的性能(显著高于基于logits的方法),但计算和存储开销较大。
本文聚焦于分析什么限制了基于logits的方法的潜力和重振logit蒸馏。
3. Rethinking Knowledge Distillation
在这一节,我们深入探究了知识蒸馏的机制。我们将KD损失重新表示为两部分的加权和,一部分与目标类相关,另一部分与非目标类相关。我们探究了知识蒸馏框架中各部分的作用,并揭示了经典KD的一些局限性。受这些结果的启发,我们进一步提出了一种新颖的logit蒸馏方法,在各种任务上取得了引人注目的性能。
3.1. Reformulating KD
符号。 对于来自第ttt类的训练样本,其分类概率可以表示为p=[p1,p2,...,pt,...,pC]∈R1×C\bold{p}=[p_1,p_2,...,p_t,...,p_C]\in\mathbb{R}^{1×C}p=[p1,p2,...,pt,...,pC]∈R1×C,其中pip_ipi是第iii类的概率,CCC是类别数目。p\bold{p}p中的每个元素都可以通过softmax函数得到:
pi=exp(zi)∑j=1Cexp(zj)(1)p_i=\frac{\mathrm{exp}(z_i)}{\sum_{j=1}^C\mathrm{exp}(z_j)}\tag{1} pi=∑j=1Cexp(zj)exp(zi)(1)其中,ziz_izi表示第iii类的logit。
为了分离与目标类相关和不相关的预测,我们定义以下符号。b=[pt,p∖t]∈R1×2\bold{b}=[p_t,p_{\setminus t}]\in\mathbb{R}^{1×2}b=[pt,p∖t]∈R1×2表示目标类(ptp_tpt)和所有其它非目标类(p∖tp_{\setminus t}p∖t)的二分类概率,可以通过下式计算得到:
pt=exp(zt)∑j=1Cexp(zj),p∖t=∑k=1,k≠tCexp(zk)∑j=1Cexp(zj)p_t=\frac{\mathrm{exp}(z_t)}{\sum_{j=1}^C\mathrm{exp}(z_j)},~p_{\setminus t}=\frac{\sum_{k=1,k\neq t}^C\mathrm{exp}(z_k)}{\sum_{j=1}^C\mathrm{exp}(z_j)} pt=∑j=1Cexp(zj)exp(zt), p∖t=∑j=1Cexp(zj)∑k=1,k=tCexp(zk)同时,我们声明p^=[p^1,...,p^t−1,p^t+1,...,p^C]∈R1×(C−1)\bold{\hat{p}}=[\hat{p}_1,...,\hat{p}_{t-1},\hat{p}_{t+1},...,\hat{p}_C]\in\mathbb{R}^{1×(C-1)}p^=[p^1,...,p^t−1,p^t+1,...,p^C]∈R1×(C−1)对非目标类(即不考虑第ttt类)中的概率进行独立建模。每个元素通过下式计算得到:
p^i=exp(zi)∑j=1,j≠tCexp(zj)(2)\hat{p}_i=\frac{\mathrm{exp}(z_i)}{\sum_{j=1,j\neq t}^C\mathrm{exp}(z_j)}\tag{2} p^i=∑j=1,j=tCexp(zj)exp(zi)(2)重新表示。 在这一部分,我们尝试用二分类概率b\bold{b}b和非目标类中的概率p^\bold{\hat{p}}p^来重新表示KD。T\mathcal{T}T和S\mathcal{S}S分别表示教师和学生。经典的KD使用KL散度作为损失函数,可写为(不失一般性,我们略去温度T):
KD=KL(pT∣∣pS)=ptTlog(ptTptS)+∑i=1,i≠tCpiTlog(piTpiS)(3)\begin{align} \mathrm{KD}&=\mathrm{KL}(\bold{p}^{\mathcal{T}}||\bold{p}^{\mathcal{S}})\\ &=p_t^{\mathcal{T}}\mathrm{log}(\frac{p_t^{\mathcal{T}}}{p_t^{\mathcal{S}}})+\sum_{i=1,i\neq t}^Cp_i^{\mathcal{T}}\mathrm{log}(\frac{p_i^{\mathcal{T}}}{p_i^{\mathcal{S}}}) \end{align}\tag{3} KD=KL(pT∣∣pS)=ptTlog(ptSptT)+i=1,i=t∑CpiTlog(piSpiT)(3)根据公式1和公式2,我们有p^i=pi/p∖t\hat{p}_i=p_i/p_{\setminus t}p^i=pi/p∖t,因此我们可以改写公式3为:
KD=ptTlog(ptTptS)+p∖tT∑i=1,i≠tCp^iT(log(p^iTp^iS)+log(p∖tTp∖tS))=ptTlog(ptTptS)+p∖tTlog(p∖tTp∖tS)⏟KL(bT∣∣bS)+p∖tT∑i=1,i≠tCp^iTlog(p^iTp^iS)⏟KL(p^T∣∣p^S)(4)\begin{align} \mathrm{KD}&=p_t^{\mathcal{T}}\mathrm{log}(\frac{p_t^{\mathcal{T}}}{p_t^{\mathcal{S}}})+p_{\setminus t}^{\mathcal{T}}\sum_{i=1,i\neq t}^C\hat{p}_i^{\mathcal{T}}(\mathrm{log}(\frac{\hat{p}_i^{\mathcal{T}}}{\hat{p}_i^{\mathcal{S}}})+\mathrm{log}(\frac{p_{\setminus t}^{\mathcal{T}}}{p_{\setminus t}^{\mathcal{S}}}))\\ &=\underbrace{p_t^{\mathcal{T}}\mathrm{log}(\frac{p_t^{\mathcal{T}}}{p_t^{\mathcal{S}}})+p_{\setminus t}^{\mathcal{T}}\mathrm{log}(\frac{p_{\setminus t}^{\mathcal{T}}}{p_{\setminus t}^{\mathcal{S}}})}_{\mathrm{KL}(\bold{b}^{\mathcal{T}}||\bold{b}^{\mathcal{S}})}+p_{\setminus t}^{\mathcal{T}}\underbrace{\sum_{i=1,i\neq t}^C\hat{p}_i^{\mathcal{T}}\mathrm{log}(\frac{\hat{p}_i^{\mathcal{T}}}{\hat{p}_i^{\mathcal{S}}})}_{\mathrm{KL}(\bold{\hat{p}}^{\mathcal{T}}||\bold{\hat{p}}^{\mathcal{S}})} \end{align}\tag{4} KD=ptTlog(ptSptT)+p∖tTi=1,i=t∑Cp^iT(log(p^iSp^iT)+log(p∖tSp∖tT))=KL(bT∣∣bS)ptTlog(ptSptT)+p∖tTlog(p∖tSp∖tT)+p∖tTKL(p^T∣∣p^S)i=1,i=t∑Cp^iTlog(p^iSp^iT)(4)然后,公式4可以改写为:
KD=KL(bT∣∣bS)+(1−ptT)KL(p^T∣∣p^S)(5)\mathrm{KD}=\mathrm{KL}(\bold{b}^{\mathcal{T}}||\bold{b}^{\mathcal{S}})+(1-p_t^{\mathcal{T}})\mathrm{KL}(\bold{\hat{p}}^{\mathcal{T}}||\bold{\hat{p}}^{\mathcal{S}})\tag{5} KD=KL(bT∣∣bS)+(1−ptT)KL(p^T∣∣p^S)(5)如公式5所示,KD损失被重新表示为两项的加权和。KL(bT∣∣bS)\mathrm{KL}(\bold{b}^{\mathcal{T}}||\bold{b}^{\mathcal{S}})KL(bT∣∣bS)表示教师和学生对目标类的二分类概率之间的相似度。因此,我们将其命名为目标类知识蒸馏(TCKD)。同时,KL(p^T∣∣p^S)\mathrm{KL}(\bold{\hat{p}}^{\mathcal{T}}||\bold{\hat{p}}^{\mathcal{S}})KL(p^T∣∣p^S)表示教师和学生对非目标类中的概率之间的相似度,命名为非目标类知识蒸馏(NCKD)。公式5可以改写为:
KD=TCKD+(1−ptT)NCKD(6)\mathrm{KD}=\mathrm{TCKD}+(1-p_t^{\mathcal{T}})\mathrm{NCKD}\tag{6} KD=TCKD+(1−ptT)NCKD(6)显然,NCKD的权重与ptTp_t^{\mathcal{T}}ptT是耦合的。
上述重新表示启发了我们研究TCKD和NCKD单独的作用,这将揭示经典的耦合表示的局限性。
3.2. Effects of TCKD and NCKD
各部分的性能增益。 我们分别研究了TCKD和NCKD在CIFAR-100上的作用。选择ResNet、WideResNet(WRN)和ShuffleNet作为训练模型,其中相同和不同的结构都考虑了。实验结果报告于表1。对于每一个教师-学生对,我们报告了以下结果:①学生基线(原始训练),②经典的KD(TCKD和NCKD都被使用),③单独地TCKD和④单独地NCKD。每个损失的权重设为1.0(包括默认的交叉熵损失)。其它实现细节与第4节相同。

直觉上,TCKD关注的是与目标类相关的知识,因为对应的损失函数只考虑二分类概率。相反,NCKD关注非目标类中的知识。我们注意到,单独使用TCKD对学生可能是无益的(例如在ShuffleNet-V1上分别获得0.02%和0.12%的增益),甚至是有害的(例如在WRN-16-2上下降2.3%,在ResNet8×4上下降3.87%)。然而,NCKD的蒸馏性能与经典的KD相当甚至更好(例如在ResNet8×4上1.76% vs. 1.13%)。消融结果表明,与目标类相关的知识可能不如非目标类中的知识重要。为了研究这一现象,我们提供如下的进一步分析。
TCKD迁移关于训练样本“难度”的知识。 根据式公式5,TCKD通过二分类任务来迁移“暗知识”,其可能与样本“难度”有关。例如,ptT=0.99p_t^{\mathcal{T}}=0.99ptT=0.99的训练样本比ptT=0.75p_t^{\mathcal{T}}=0.75ptT=0.75的训练样本“更容易”学习。由于TCKD传达了训练样本的“难度”,我们猜想当训练数据变得具有挑战性时,TCKD的有效性将显现出来。然而,CIFAR-100训练集是容易拟合的(收敛后在CIFAR-100上的训练精度可以达到100%)。因此,教师提供的“难度”知识是无用信息。本部分从3个角度进行实验验证:训练数据越困难,TCKD能提供的好处越多(这些角度的所有实验都是和NCKD一起进行的,因为根据表1的结果,我们推断TCKD不应该单独使用)。
①应用强大的增广是一种增加训练数据难度的直接方法。我们在CIFAR-100上利用AutoAugment训练ResNet32×4模型作为教师,达到了81.29%的top-1验证准确率。对于学生,我们训练使用/不使用TCKD的ResNet8×4和ShuffleNet-V1模型。表2的结果表明,如果应用强大的增广,TCKD可以获得显著的性能增益。

②噪声标签也可以增加训练数据的难度。我们在CIFAR-100上以{0.1,0.2,0.3}\{0.1,0.2,0.3\}{0.1,0.2,0.3}的对称噪声比训练ResNet32×4模型作为教师和ResNet8×4作为教师。如表3所示,结果表明TCKD在更嘈杂的训练数据上取得了更多的性能提升。

③还考虑了具有挑战性的数据集(例如ImageNet)。由表4可知,TCKD在ImageNet上可以带来+0.32%的性能增益。

综上所述,我们通过实验各种策略增加训练数据的难度(例如强大的增广、噪声标签和困难任务),证明了TCKD的有效性。实验结果验证了在更具挑战性的训练数据上蒸馏知识时,关于训练样本“难度”的知识可能更有益处。
NCKD是logit蒸馏有效但极大地被抑制的重要原因。 有趣的是,我们在表1中注意到,当仅使用NCKD时,性能与经典的KD相当甚至更好。这表明非目标类中的知识对logit蒸馏至关重要,可能是重要的“暗知识”。然而,通过回顾公式5,我们注意到NCKD损失是和(1−ptT)(1-p_t^{\mathcal{T}})(1−ptT)耦合的,其中ptTp_t^{\mathcal{T}}ptT表示教师在目标类上的置信度。因此,更自信的预测会导致更小的NCKD权重。我们认为教师在训练样本中越自信,其提供的知识就越可靠和有价值。然而,损失权重被这种自信的预测高度地抑制。我们认为这一事实会限制知识迁移的有效性,这是由于我们在公式5中对KD重新表示而首次研究的。
我们设计了一个消融实验来验证预测良好的样本确实比其它样本迁移了更好的知识。首先我们根据ptTp_t^{\mathcal{T}}ptT对训练样本进行排序,并将其平均地拆分为两个子集。为清晰起见,一个子集包含了前50%ptTp_t^{\mathcal{T}}ptT而交叉熵损失仍然在整个集合上的样本,而剩余的样本则在另一个子集。然后我们在每个子集上训练使用NCKD的学生网络来比较性能增益(交叉熵损失仍然在整个集合上)。表5显示,使用NCKD在前50%的样本上取得了更好的性能,表明预测良好的样本的知识比其它样本更丰富。然而,预测良好的样本的损失权重被教师的高置信度所抑制。

3.3. Decoupled Knowledge Distillation
至此,我们将经典的KD损失转化为两个独立部分的加权和,并进一步验证了TCKD的有效性和揭示了NCKD的抑制。具体来说,TCKD迁移关于训练样本“难度”的知识。TCKD在更具挑战性的训练数据上可以获得更显著的改进。NCKD迁移非目标类中的知识,在权重(1−ptT)(1-p_t^{\mathcal{T}})(1−ptT)相对较小的情况下会被抑制。
直觉上,TCKD和NCKD都是必须的、至关重要的。然而,在经典的KD形式中,TCKD和NCKD从以下几个方面耦合:
- 一方面,NCKD与(1−ptT)(1-p_t^{\mathcal{T}})(1−ptT)耦合,它可能在预测良好的样本上抑制NCKD。由于表5中的结果表明预测良好的样本可以带来更多的性能增益,因此这种耦合形式会限制NCKD的有效性。
- 另一方面,NCKD和TCKD的权重在经典的KD框架下是耦合的。它不允许为了平衡重要性而改变各项的权重。我们认为TCKD和NCKD应该分开考虑,因为它们的贡献来自不同方面。
得益于我们对KD的重新表示,我们提出了一种新的名为解耦知识蒸馏(DKD)的logit蒸馏方法来解决上述问题。我们提出的DKD将TCKD和NCKD独立地考虑在一个解耦的形式中,如图1b所示。具体来说,我们引入两个超参数α\alphaα和β\betaβ,分别作为TCKD和NCKD的权重。DKD的损失函数可以写成如下形式:
DKD=αTCKD+βNCKD(7)\mathrm{DKD}=\alpha\mathrm{TCKD}+\beta\mathrm{NCKD}\tag{7} DKD=αTCKD+βNCKD(7)在DKD中,将会抑制NCKD有效性的(1−ptT)(1-p_t^{\mathcal{T}})(1−ptT)替换为β\betaβ。此外,它还允许调整α\alphaα和β\betaβ来平衡TCKD和NCKD的重要性。通过解耦NCKD和TCKD,DKD为logit蒸馏提供了一种高效灵活的方式。算法1提供了PyTorch-like风格的DKD伪代码。

4. Experiments
在图像分类和目标检测任务上进行实验,包括CIFAR-100、ImageNet和MS-COCO数据集。
4.1. Main Results
首先,我们分别证明了解耦①NCKD和(1−ptT)(1-p_t^{\mathcal{T}})(1−ptT)以及②NCKD和TCKD所带来的改进。然后,我们在图像分类和目标检测任务上测试了我们的方法。
消融:α\alphaα和β\betaβ。 下面两个表格报告了不同α\alphaα和β\betaβ的学生准确率(%)。ResNet32×4和ResNet8×4分别设为教师和学生。首先,我们在第一个表中证明解耦(1−ptT)(1-p_t^{\mathcal{T}})(1−ptT)和NCKD可以带来尚可的性能增益(73.63% vs. 74.79%)。然后,我们证明了解耦NCKD和TCKD的权重有助于进一步改进(74.79% vs. 76.32%)。此外,第二个表表明TCKD是不可或缺的,在1.0左右不同的α\alphaα下TCKD带来的改进是稳定的(出于简化我们在第一个表中将α\alphaα固定为1.0,在第二个表中将β\betaβ固定为8.0,因为它在第一个表中取得了最佳性能)。

CIFAR-100图像分类。 DKD在CIFAR-100上的性能对比,具体的实验结论可以参照原文。


ImageNet图像分类。 DKD在ImageNet上的性能对比,具体的实验结论可以参照原文。

MS-COCO目标检测。 正如之前的工作所讨论的,目标检测任务的性能在很大程度上依赖于深度特征定位感兴趣目标的质量。这个规则也体现在检测器之间的知识迁移,即特征模仿(feature mimicking)是至关重要的,因为logits不能为目标定位提供知识。如表10所示,单独应用DKD难以达到优异的性能,但有望超越经典的KD。因此,我们引入了基于特征的蒸馏方法ReviewKD来获得令人满意的结果。可以观察到我们的DKD可以进一步提升AP指标,即使ReviewKD的蒸馏性能已经相当高了。总之,通过将我们的DKD与基于特征的蒸馏方法相结合,在目标检测任务上获得了新的SOTA结果。

4.2. Extensions
为了更好地理解DKD,我们从四个方面进行了扩展。首先,我们全面比较了DKD与具有代表性的SOTA方法的训练效率。然后,我们提供了一个新的视角来解释为什么更大的模型并不总是更好的教师,并通过使用DKD缓解了这个问题。此外,我们考察了DKD学习到的深度特征的可迁移性。我们还展示了一些可视化结果来验证DKD的优越性。
训练效率。 DKD取得了很好的训练开销和模型性能(例如训练时间和额外的参数)之间的折衷,具体的实验结论可以参照原文。

提高大型教师的性能。 之所以更大的模型不一定是更好的教师,是因为NCKD的抑制,即(1−ptT)(1-p_t^{\mathcal{T}})(1−ptT)会随着教师变大而变小。具体的实验结论可以参照原文。

特征可迁移性。 我们通过实验来评估深度特征的可迁移性,以验证我们的DKD迁移了更多的可泛化的知识。具体的实验结论可以参照原文。

可视化。 ①DKD有利于深度特征的可区分性。②DKD有助于学生输出与教师更相似的logits。具体的实验结论可以参照原文。

5. Discussion and Conclusion
本文通过将经典的知识蒸馏损失重新表示为目标类知识蒸馏(TCKD)和非目标类知识蒸馏(NCKD)两部分,为解释logit蒸馏提供了新的视角。这两部分的作用被分别研究和证明。更重要的是,我们揭示了KD的耦合形式限制了知识迁移的有效性和灵活性。为了克服这些问题,我们提出了解耦知识蒸馏(DKD),在用于图像分类和目标检测任务的CIFAR-100、ImageNet和MS-COCO数据集上取得了显著的改进。此外,DKD在训练效率和特征可迁移性方面的优越性也被证明。我们希望本文对未来logit蒸馏的研究有所贡献。
局限性和未来的工作。 下面讨论值得注意的局限性。在目标检测任务上,DKD无法超越目前SOTA的基于特征的方法(例如ReviewKD),因为基于logits的方法无法迁移定位知识。除此之外,我们在补充材料中对如何调整β\betaβ提供了直觉上的指导。然而,蒸馏性能与β\betaβ之间的严格相关性并没有得到充分的研究,这将是我们未来的研究方向。
相关文章:

知识蒸馏论文阅读:DKD算法笔记
标题:Decoupled Knowledge Distillation 会议:CVPR2022 论文地址:https://ieeexplore.ieee.org/document/9879819/ 官方代码:https://github.com/megvii-research/mdistiller 作者单位:旷视科技、早稻田大学、清华大学…...
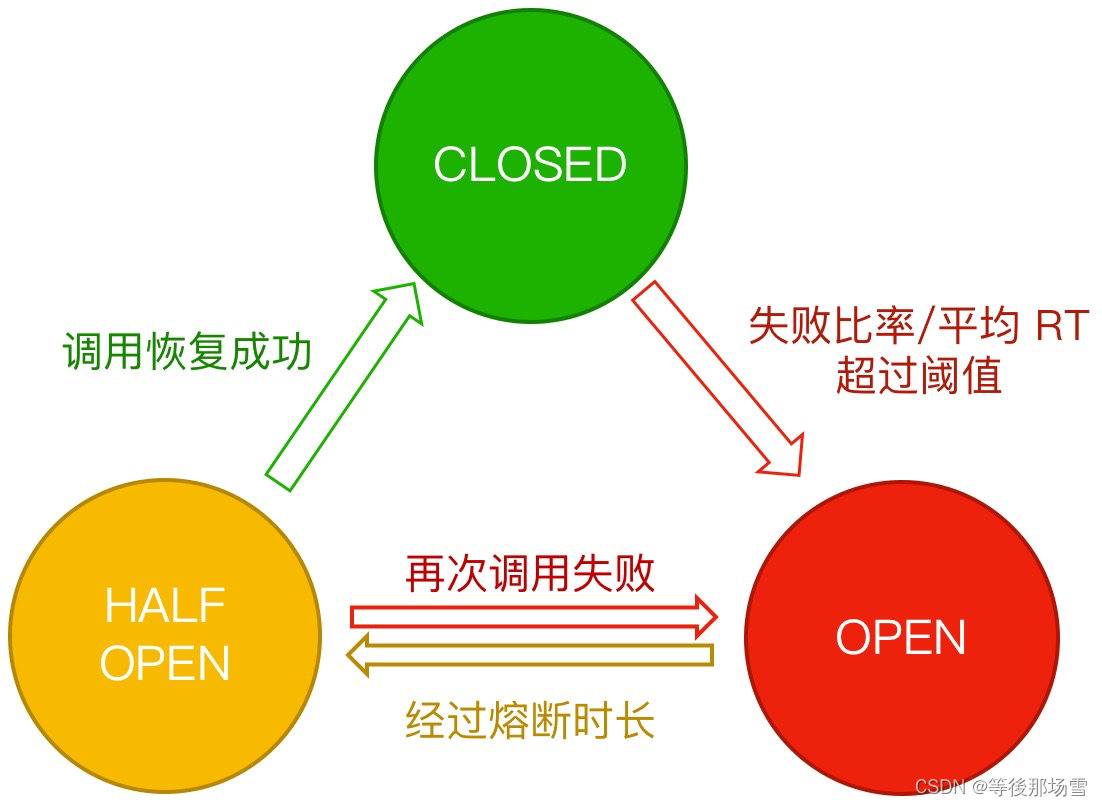
Sentinel架构篇 - 熔断降级
熔断降级 概念 除了流量控制以外,对调用链路中不稳定的资源进行熔断降级也是保障高可用的重要措施之一。一个服务常常会调用其它模块,可能是一个远程服务、数据库、或者第三方 API 等。然而,被依赖的服务的稳定性是不能保证的。如果依赖的服…...

shell脚本的一些记录 与jenkins的介绍
shell 脚本的执行 sh ***.sh shell脚本里面的命令 其实就是终端执行一些命令 shell 连接服务器 可以直接ssh连接 但是这样最好是无密码的 不然后面的命令就不好写了 换而言之有密码得 不好写脚本 需要下载一些expect的插件之类的才可以 判断语句 的示例 需要注意的是…...

JVM的了解与学习
一:jvm是什么 jvm是java虚拟机java Virtual Machine的缩写 jdk包含jre和java DevelopmentTools 二:什么是java虚拟机 虚拟机是一种抽象化的计算机,通过在实际的计算机上仿真模拟各种计算机功能来实现的。java虚拟机有自己完善的硬体结构,如处理器、堆栈、寄存器等,还有…...

提升数字品牌的5个技巧
“品牌”或“品牌推广”的概念通常用于营销。因为建立您的企业品牌对于产品来说极其重要,品牌代表了您与客户互动的身份和声音。今天,让我们来看看在数字领域提升品牌的一些有用的技巧。如何在数字领域提升您的品牌?在了解这些技巧之前&#…...

java通过反射获取加了某个注解的所有的类
有时候我们会碰到这样的情况:有n个场景,每个场景都有自己的逻辑,即n个处理逻辑,这时候我们就需要通过某个参数的值代表这n个场景,然后去加载每个场景不同的bean对象,即不同的类,这些类中都有一个…...

Warshall算法
🚀write in front🚀 📜所属专栏:> 算法 🛰️博客主页:睿睿的博客主页 🛰️代码仓库:🎉VS2022_C语言仓库 🎡您的点赞、关注、收藏、评论,是对我…...
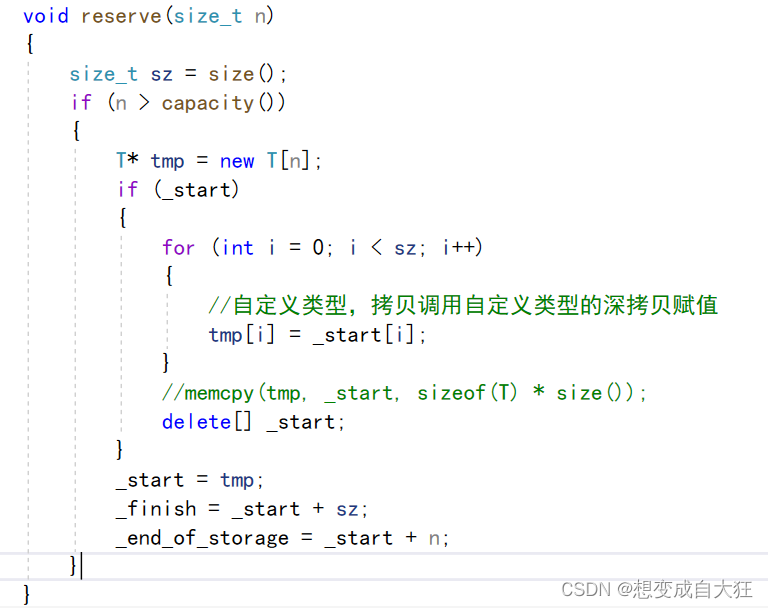
vector中迭代器失效的问题及解决办法
目录 vector常用接口 vector 迭代器失效问题 vector中深浅拷贝问题 vector的数据安排以及操作方式,与array非常相似。两者的唯一差别在于空间的运用的灵活性。array 是静态空间,一旦配置了就不能改变;要换个大(或小) 一点的房子&#x…...
【蓝桥杯刷题训练营】day05
1 数的分解 拆分成3个数相加得到该数 然后采用了一种巨愚蠢的办法: int main() {int count 0;int a 2;int b 0;int c 1;int d 9;int a1, a2, a3;int c1, c2, c3;int d1, d2, d3;for (a1 0; a1 < 2; a1){for (a2 0; a2 < 2; a2){for (a3 0; a3 <…...

线程中断interrupt导致sleep产生的InterruptedException异常
强制当前正在执行的线程休眠(暂停执行),以“减慢线程”。 Thread.sleep(long millis)和Thread.sleep(long millis, int nanos)静态方法当线程睡眠时,它睡在某个地方,在苏醒之前不会返回到可运行状态。 当睡眠时间到期…...
ubuntu的快速安装与配置
文章目录前言一、快速安装二 、基础配置1 Sudo免密码2 ubuntu20.04 pip更新源3 安装和配置oneapi(infort/mpi/mkl) apt下载第一次下载的要建立apt源apt下载(infort/mpi/mkl)4 安装一些依赖库等5 卸载WSLpython总结前言 win11系统 ubuntu20.04 提示:以下…...
)
人工智能AI工具汇总(AIGC ChatGPT时代个体崛起)
NameCategoryWebsiteDescription描述《AIGC时代:超级个体的崛起》小报童https://xiaobot.net/p/SuperIndividual 介绍AIGC,ChatGPT,使用技巧与搞钱方式。Masterpiece Studio3Dhttps://masterpiecestudio.comSimplifying 3D Creation with AI…...
【rust-grpc-proxy】在k8s中,自动注入代理到pod中,再不必为grpc调试而烦恼
目录前言原理sidecarwebhook实现安装k8s设置webhook使用尾语前言 rust-grpc-proxy 目前功能基本完善。是时候上环境开始应用了。 之前考虑是gateway模式或者sidecar模式。 思考良久之后,觉得两种模式都有使用场景,那就都支持。本次就带来sidecar模式的食…...

VisualStudio2022制作多项目模板及Vsix插件
一、安装工作负载 在vs2022上安装“visual studio扩展开发 ”工作负载 二、制作多项目模板 导出项目模板这个我就不再多说了(项目→导出模板→选择项目模板,选择要导出的项目→填写模板信息→完成)。 1.准备模板文件 将解决方案中的多个…...

仿写简单IOC
目录 TestController类: UserService类: 核心代码SpringIOC: Autowired和Component注解 SpringIOCTest 类 编辑 总结: TestController类: Component public class TestController {Autowiredprivate UserService userService;public void test…...
liunx下安装node exporter
1 建立文件夹 cd /opt mkdir software 下载最新的包,并解压 https://prometheus.io/download/ 下载 curl -LO https://github.com/prometheus/node_exporter/releases/download/v0.18.1/node_exporter-0.18.1.linux-amd64.tar.gz 3.解压 tar -xvf node_exporter-0.…...

lambda函数
Lambda(函数指针)lambda 是c11非常重要也是最常用的特性之一,他有以下优点:可以就地匿名定义目标函数或函数对象,不需要额外写一个函数lambda表达式是一个匿名的内联函数lambda表达式定义了一个匿名函数,语法如下:[cap…...

【Python入门第二十七天】Python 日期
Python 日期 Python 中的日期不是其自身的数据类型,但是我们可以导入名为 datetime 的模块,把日期视作日期对象进行处理。 实例 导入 datetime 模块并显示当前日期: import datetimex datetime.datetime.now() print(x)运行实例 2023-0…...

C++基础知识【5】数组和指针
目录 一、概述 数组 指针 二、数组 2.1、数组的声明 2.2、数组的初始化 2.3、数组的访问 2.4、多维数组 2.5、数组作为函数参数 三、指针 3.1、指针的声明 3.2、指针的赋值 3.3、指针的访问 3.4、指针运算 3.5、指针数组和数组指针 3.6、二级指针 四、数组和指…...

Vim使用操作命令笔记
Vim使用操作命令笔记在普通模式下,输入 : help tutor 就可以进入vim的教学 在 terminal 中输入 vim 文件名 就可以打开文件 vim有两种模式 normal mode (普通模式)→ 指令操作 insert mode (输入模式&…...

AI-调查研究-01-正念冥想有用吗?对健康的影响及科学指南
点一下关注吧!!!非常感谢!!持续更新!!! 🚀 AI篇持续更新中!(长期更新) 目前2025年06月05日更新到: AI炼丹日志-28 - Aud…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Springcloud:Eureka 高可用集群搭建实战(服务注册与发现的底层原理与避坑指南)
引言:为什么 Eureka 依然是存量系统的核心? 尽管 Nacos 等新注册中心崛起,但金融、电力等保守行业仍有大量系统运行在 Eureka 上。理解其高可用设计与自我保护机制,是保障分布式系统稳定的必修课。本文将手把手带你搭建生产级 Eur…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...

LLM基础1_语言模型如何处理文本
基于GitHub项目:https://github.com/datawhalechina/llms-from-scratch-cn 工具介绍 tiktoken:OpenAI开发的专业"分词器" torch:Facebook开发的强力计算引擎,相当于超级计算器 理解词嵌入:给词语画"…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

Rapidio门铃消息FIFO溢出机制
关于RapidIO门铃消息FIFO的溢出机制及其与中断抖动的关系,以下是深入解析: 门铃FIFO溢出的本质 在RapidIO系统中,门铃消息FIFO是硬件控制器内部的缓冲区,用于临时存储接收到的门铃消息(Doorbell Message)。…...

项目部署到Linux上时遇到的错误(Redis,MySQL,无法正确连接,地址占用问题)
Redis无法正确连接 在运行jar包时出现了这样的错误 查询得知问题核心在于Redis连接失败,具体原因是客户端发送了密码认证请求,但Redis服务器未设置密码 1.为Redis设置密码(匹配客户端配置) 步骤: 1).修…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
