【论文阅读】Robust Multi-Instance Learning with Stable Instances
1、摘要与引言
以往的MIL算法遵循i.i.d假设:训练样本与测试样本都分别来自于同一分布中,而这一假设往往与现实应用中有所出入。研究人员通过计算训练样本与测试样本之间的密度比对训练样本进行加权,以解决分布变化带来的问题。
分布的变化发生的原因有许多,诸如:训练数据与测试数据是在不同的时间或不同的地点收集的。当分布发生变化时,由于无法区分因果实例与噪声实例,算法的性能会发生改变。当训练集与测试集分布不同时,噪音实例和标签之间的关联性将不一致。

如图所示,训练集中的数据在夏天收集的,因果实例是狗,噪声实例是草,并与因果实例高度相关。而测试集中的数据是在冬季收集的,背景大多是雪,而雪则成为了噪音实例。若不考虑分布变化,由于训练样本与测试样本的分布差异,标准有监督算法通常倾向于预测草中有狗的图像为正,而雪中有狗的图像为负。
本文提出了第一个解决MIL中分布变化问题的算法框架,并且此方法不需要无标签的测试数据集。将实例分为三类:因果实例(狗勾)、噪声实例(草)和负实例(其他背景实例),解决MIL中的分布变化问题。
2、Stable Multi-instance Learning Framework
因果实例:考虑将实例xxx加入到包XjX_{j}Xj中并观察包标签YYY,并通过观察标签是否发生变化来确定实例xxx与标签YYY是否存在因果关系。换句话说,若实例xxx与标签YYY存在因果关系,则将它添加到一个负包中时,该包的标签将从负变为正。若实例xxx与标签YYY不存在因果关系,则标签不会发生改变。这种因果关系不会因训练数据或测试数据而发生改变。
噪音实例:噪音实例要么与因果实例和包标签中的其中一个有关联,要么与两者都有关联。如:草和雪都属于噪音实例。虽然草和雪都和因果实例以及标签存在关联,但它们的相关性在训练集与测试集中有所不同。
负实例:与标签无关联的实例,即与包标签无任何关联的随机背景对象。
由于因果实例与标签之间的关系不会因训练集与测试集之间的分布不同而改变,基于因果实例的MIL分类器将获得更加稳定的性能。
2.1、Learning Causal Instances from Experiment
我们只考虑从正包中找出因果实例。∪B+\cup \mathcal{B}^{+}∪B+表示包含着来自正包中的所有实例组成的实例池,池中实例x∈∪B+x\in \cup \mathcal{B}^{+}x∈∪B+。为了确定实例xxx是否为因果实例,需要计算实例xxx对包标签YYY的因果效应,通常定义为加入实例后的预期标签与加入实例前的预测标签之间的差异性:
T(x)=E[Y(T=1)]−E[Y(T=0)].(1)\mathcal{T}\left ( x \right ) =\mathbb{E}\left [ Y\left ( T=1 \right ) \right ] -\mathbb{E}\left [ Y(T=0) \right ] .\tag{1}T(x)=E[Y(T=1)]−E[Y(T=0)].(1)
其中,Y(T=1)Y(T=1)Y(T=1)表示预期标签,即:候选实例xxx出现在包中;Y(T=0)Y(T=0)Y(T=0)表示预期标签,即:候选实例xxx未出现在包中。
我们可以通过将候选实例xxx添加到一个包中(若包内不存在候选实例)或从包中移出实例xxx(若包内存在候选实例)来获得处理过或未处理过的包。因此,可以通过数据与oracle分类器提供的期望差异来评估因果效益:
T(x)=E[Y∗(T=1)]−E[Y∗(T=0)].(2)\mathcal{T}\left ( x \right ) =\mathbb{E}\left [ Y^{*}\left ( T=1 \right ) \right ] -\mathbb{E}\left [ Y^{*}(T=0) \right ] .\tag{2}T(x)=E[Y∗(T=1)]−E[Y∗(T=0)].(2)
其中,Y∗Y^{*}Y∗表示经处理后(将候选因果实例加入包中)的包标签。
由标准MIL假设知:向正包中添加任何实例或是从负包中移除任何实例都不会改变包的标签。因此E[Y∗∣Y=0,T=0]=0,E[Y∗∣Y=1,T=1]=1\mathbb{E}\left [ Y^{*}|Y=0,T=0 \right ]=0,\mathbb{E}\left [ Y^{*}|Y=1,T=1 \right ]=1E[Y∗∣Y=0,T=0]=0,E[Y∗∣Y=1,T=1]=1。同时,对正包进行处理时有两种可能性:
①预处理包中含有除xxx以外的正实例;
②预处理包中只含有xxx作为其正实例。
2.2、Learning Stable Instances from Data
为了获得稳定实例,首先使用训练集数据训练一个多示例分类算法A\mathcal{A}A,并使用AAA表示A\mathcal{A}A返回的分类器。对于每一个候选实例xxx,我们构建一组包集合,其中包含了m−m^{-}m−个treated bags。每个treated bag都是通过向负包Xi−X_{i}^{-}Xi−中添加候选实例xxx构建的。
对于每个treated bag,我们再使用之前训练得到的分类器AAA来预测其标签。最后,我们使用treated bag的预测标签均值来估计预期:
T^(x)=1m−∑i=1m−A(Xix)\hat{\mathcal{T}}(x)=\frac{1}{m^{-}}\sum_{i=1}^{m^{-}}A(X_{i}^{x})T^(x)=m−1i=1∑m−A(Xix)
估计后,选择得分sss高于T\mathcal{T}T的候选实例作为稳定实例。
相关文章:

【论文阅读】Robust Multi-Instance Learning with Stable Instances
1、摘要与引言 以往的MIL算法遵循i.i.d假设:训练样本与测试样本都分别来自于同一分布中,而这一假设往往与现实应用中有所出入。研究人员通过计算训练样本与测试样本之间的密度比对训练样本进行加权,以解决分布变化带来的问题。 分布的变化发…...

洛谷 P5116 [USACO18DEC]Mixing Milk B
题目链接:P5116 [USACO18DEC]Mixing Milk B - 洛谷 | 计算机科学教育新生态 (luogu.com.cn) 题目描述 农业,尤其是生产牛奶,是一个竞争激烈的行业。Farmer John 发现如果他不在牛奶生产工艺上有所创新,他的乳制品生意可能就会受…...
【独家】)
华为OD机试 - 最左侧冗余覆盖子串(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:最左侧冗…...

实验7 图像水印
本次实验大部分素材来源于山大王成优老师的讲义以及冈萨雷斯(MATLAB版),仅作个人学习笔记使用,禁止用作商业目的。 文章目录一、实验目的二、实验例题1. 数字图像水印技术2. 可见水印的嵌入3. 不可见脆弱水印4. 不可见鲁棒水印一、…...

如何实现大文件断点续传、秒传
大家先来了解一下几个概念: 「文件分块」:将大文件拆分成小文件,将小文件上传\下载,最后再将小文件组装成大文件; 「断点续传」:在文件分块的基础上,将每个小文件采用单独的线程进行上传\下载&…...

备战蓝桥python——完全平方数
完全平方数 链接: 完全平方数 暴力解法: n int(input()) for i in range(1, n1):if(((i*n)**0.5)%10.0):print(i)break运用数论相关知识求解 任意一个正整数都可以被分解成若干个质数乘积的形式,例如 :2022∗5120 \ 2^{2}*5^{1}\,20 22∗51 由此…...
WebRTC中的NAT穿透
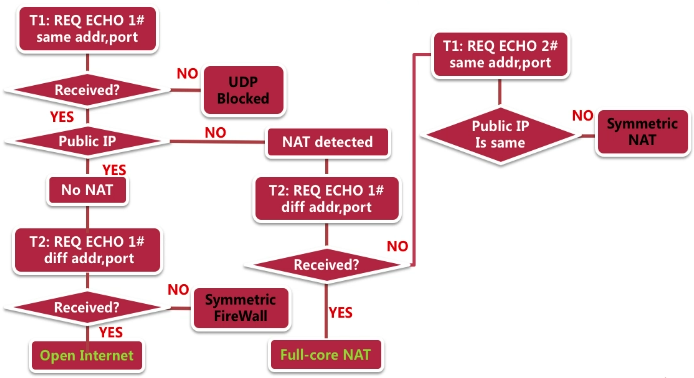
NAT简介 我们知道,WebRTC会按照内网、P2P、中转的顺序来尝试连接。在大部分的情况下,实际是使用P2P或者中转的。这里P2P的场景主要使用的技术就是NAT穿透。 我们先简单了解下NAT。NAT在真实网络中是常见的,它的出现一是为了解决ipv4地址不够…...
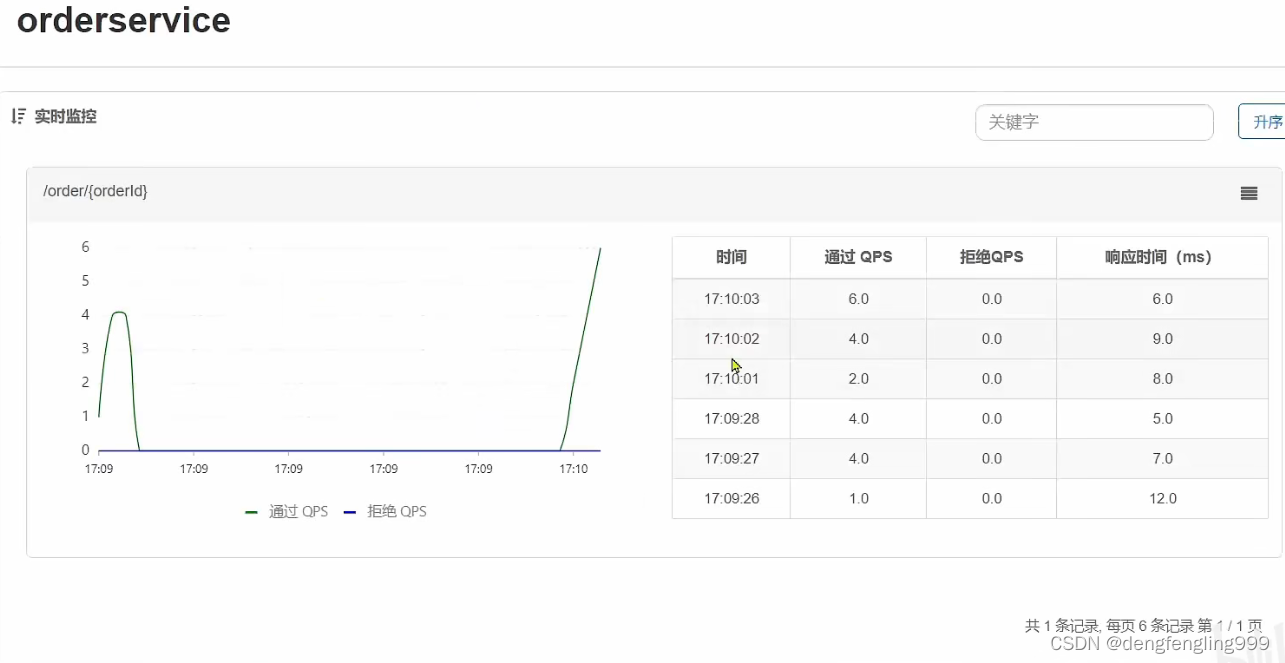
SpringCloud-高级篇(一)
目录: (1)初识Sentinel-雪崩问题的解决方案 (2)服务保护Sentinel和Hystrix对比 (3)Sentinel初始-安转控制台 (4)整合微服务和Sentinel 微服务高级篇 (1&…...
电脑自动重启是什么原因?详细解说
案例:电脑自动重启是什么原因? “一台用了一年的电脑,最近使用,每天都会一两次莫名其妙自动重启,看了电脑错误日志,看不懂什么意思,一直找不到答案。有没有高手知道怎么解决这个问题的。” 当…...

2023美国大学生数学建模竞赛E题思路
problem 背景: 光污染用于描述过度或不良使用人造光。我们称之为光污染的一些现象包括光侵入、过度照明和光杂波。在大城市,太阳落山后,这些现象最容易在天空中看到:然而,它们也可能发生在更偏远的地区。 光污染会改变我们对夜空…...

蓝桥杯三月刷题 第五天
文章目录💥前言😉解题报告💥数的分解🤔一、思路:😎二、代码:💥前言 上午没写,下午写了会被朋友拉出去耍,被冷风吹到了,而且被他坑了,根本没有玩骑…...
Echarts 水波图实现
开发的项目中需要实现这样一个水波图,例如下图在echarts官网中找了很久没找到,后面是在Echarts社区中找到的,实现了大部分的样式,但是还有一些数据的展示没有实现。水波图的数值展示是默认整数百分比,我的需求是需要保…...
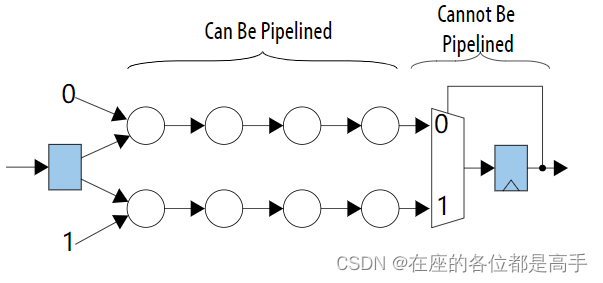
逻辑优化基础-shannon decomposition
1. 简介 在逻辑综合中,香农分解(Shannon decomposition)是一种常用的布尔函数分解方法。它将一个布尔函数分解为两个子函数的和,其中每个子函数包含一个布尔变量的取反和非取反的部分。 具体来说,假设对于一个布尔函…...

Java中线程池的创建与使用
前言:默认线程池的弊端在线程池应用中,参考阿里巴巴java开发规范:线程池不允许使用Executors去创建,不允许使用系统默认的线程池,推荐通过ThreadPoolExecutor的方式,这样的处理方式让开发的工程师更加明确&…...

关于HashMap与OkHttp的使用
写了一个okhttp的post请求方法,添加参数很麻烦,需要封装: //post请求public static void sendOkHttpRequestPost(String address , Callback callback) {OkHttpClient client new OkHttpClient();// 创建表单参数RequestBodyRequestBody fo…...
【独家】)
华为OD机试 - 单词倒序(C 语言解题)【独家】
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 使用说明本期题目:单词倒序…...
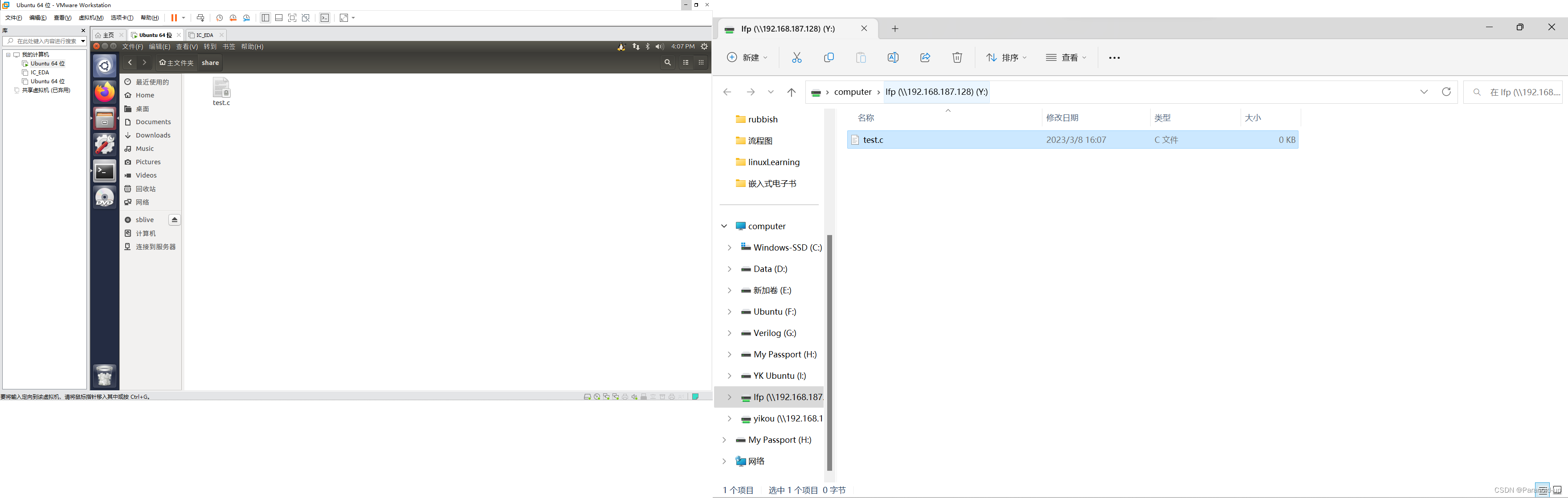
搭建Samba服务器
搭建Samba服务器 文章目录搭建Samba服务器samba安装安装命令配置-ubuntu侧为samba服务器创建一个共享目录share创建使用该共享文件夹的账号修改samba服务器配置文件重启samba服务windows创建映射1.点击映射网络驱动器2.输入Ubuntu中的ip地址及其用户信息3.输入用户信息及其密码…...
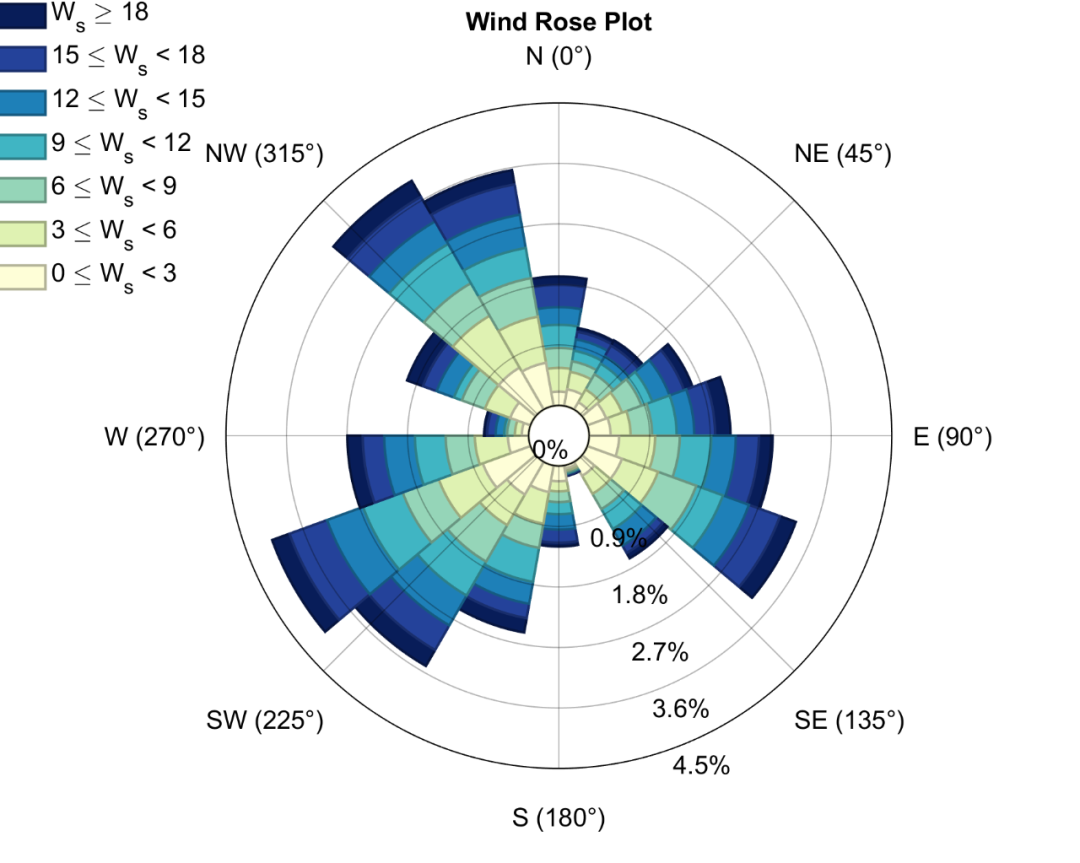
Matlab进阶绘图第5期—风玫瑰图(WindRose)
风玫瑰图(Wind rose diagram)是一种特殊的极坐标堆叠图/统计直方图,其能够直观地表示某个地区一段时期内风向、风速的发生频率。 风玫瑰图在建筑规划、环保、风力发电、消防、石油站设计、海洋气候分析等领域都有重要作用,所以在一些顶级期刊中也能够看…...
:数仓报表场景☞通过执行计划详解”行转列”,”列转行”是如何实现的)
【SQL开发实战技巧】系列(二十四):数仓报表场景☞通过执行计划详解”行转列”,”列转行”是如何实现的
系列文章目录 【SQL开发实战技巧】系列(一):关于SQL不得不说的那些事 【SQL开发实战技巧】系列(二):简单单表查询 【SQL开发实战技巧】系列(三):SQL排序的那些事 【SQL开发实战技巧…...

UE5 学习系列(三)创建和移动物体
这篇博客是该系列的第三篇,是在之前两篇博客的基础上展开,主要介绍如何在操作界面中创建和拖动物体,这篇博客跟随的视频链接如下: B 站视频:s03-创建和移动物体 如果你不打算开之前的博客并且对UE5 比较熟的话按照以…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

ESP32读取DHT11温湿度数据
芯片:ESP32 环境:Arduino 一、安装DHT11传感器库 红框的库,别安装错了 二、代码 注意,DATA口要连接在D15上 #include "DHT.h" // 包含DHT库#define DHTPIN 15 // 定义DHT11数据引脚连接到ESP32的GPIO15 #define D…...

C++中string流知识详解和示例
一、概览与类体系 C 提供三种基于内存字符串的流,定义在 <sstream> 中: std::istringstream:输入流,从已有字符串中读取并解析。std::ostringstream:输出流,向内部缓冲区写入内容,最终取…...

k8s业务程序联调工具-KtConnect
概述 原理 工具作用是建立了一个从本地到集群的单向VPN,根据VPN原理,打通两个内网必然需要借助一个公共中继节点,ktconnect工具巧妙的利用k8s原生的portforward能力,简化了建立连接的过程,apiserver间接起到了中继节…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

深入解析C++中的extern关键字:跨文件共享变量与函数的终极指南
🚀 C extern 关键字深度解析:跨文件编程的终极指南 📅 更新时间:2025年6月5日 🏷️ 标签:C | extern关键字 | 多文件编程 | 链接与声明 | 现代C 文章目录 前言🔥一、extern 是什么?&…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

NXP S32K146 T-Box 携手 SD NAND(贴片式TF卡):驱动汽车智能革新的黄金组合
在汽车智能化的汹涌浪潮中,车辆不再仅仅是传统的交通工具,而是逐步演变为高度智能的移动终端。这一转变的核心支撑,来自于车内关键技术的深度融合与协同创新。车载远程信息处理盒(T-Box)方案:NXP S32K146 与…...

20个超级好用的 CSS 动画库
分享 20 个最佳 CSS 动画库。 它们中的大多数将生成纯 CSS 代码,而不需要任何外部库。 1.Animate.css 一个开箱即用型的跨浏览器动画库,可供你在项目中使用。 2.Magic Animations CSS3 一组简单的动画,可以包含在你的网页或应用项目中。 3.An…...