C++基础了解-05-C++常量
@C++常量
一、C++常量
常量是固定值,在程序执行期间不会改变。这些固定的值,又叫做字面量。
常量可以是任何的基本数据类型,可分为整型数字、浮点数字、字符、字符串和布尔值。
常量就像是常规的变量,只不过常量的值在定义后不能进行修改
二、整数常量
整数常量可以是十进制、八进制或十六进制的常量。前缀指定基数:0x 或 0X 表示十六进制,0 表示八进制,不带前缀则默认表示十进制。
整数常量也可以带一个后缀,后缀是 U 和 L 的组合,U 表示无符号整数(unsigned),L 表示长整数(long)。后缀可以是大写,也可以是小写,U 和 L 的顺序任意。
下面列举几个整数常量的实例:
212 // 合法的
215u // 合法的
0xFeeL // 合法的
078 // 非法的:8 不是八进制的数字
032UU // 非法的:不能重复后缀
以下是各种类型的整数常量的实例:
85 // 十进制
0213 // 八进制
0x4b // 十六进制
30 // 整数
30u // 无符号整数
30l // 长整数
30ul // 无符号长整数
三、浮点常量
浮点常量由整数部分、小数点、小数部分和指数部分组成。您可以使用小数形式或者指数形式来表示浮点常量。
当使用小数形式表示时,必须包含整数部分、小数部分,或同时包含两者。当使用指数形式表示时, 必须包含小数点、指数,或同时包含两者。带符号的指数是用 e 或 E 引入的。
下面列举几个浮点常量的实例:
3.14159 // 合法的
314159E-5L // 合法的
510E // 非法的:不完整的指数
210f // 非法的:没有小数或指数
.e55 // 非法的:缺少整数或分数
四、布尔常量
布尔常量共有两个,它们都是标准的 C++ 关键字:
true 值代表真。
false 值代表假。
我们不应把 true 的值看成 1,把 false 的值看成 0
五、字符常量
字符常量是括在单引号中。如果常量以 L(仅当大写时)开头,则表示它是一个宽字符常量(例如 L’x’),此时它必须存储在 wchar_t 类型的变量中。否则,它就是一个窄字符常量(例如 ‘x’),此时它可以存储在 char 类型的简单变量中。
字符常量可以是一个普通的字符(例如 ‘x’)、一个转义序列(例如 ‘\t’),或一个通用的字符(例如 ‘\u02C0’)。
在 C++ 中,有一些特定的字符,当它们前面有反斜杠时,它们就具有特殊的含义,被用来表示如换行符(\n)或制表符(\t)等。下表列出了一些这样的转义序列码:

#include <iostream>
using namespace std;int main()
{cout << "Hello\tWorld\n\n";return 0;
}
执行结果:
Hello World
六、字符串常量
字符串字面值或常量是括在双引号 “” 中的。一个字符串包含类似于字符常量的字符:普通的字符、转义序列和通用的字符。
您可以使用 \ 做分隔符,把一个很长的字符串常量进行分行。
下面的实例显示了一些字符串常量:
#include <iostream>
#include <string>
using namespace std;int main() {string greeting = "hello, runoob";cout << greeting;cout << "\n"; // 换行符string greeting2 = "hello, \runoob";cout << greeting2;return 0;
}
七、定义常量
在 C++ 中,有两种简单的定义常量的方式:
使用 #define 预处理器。
使用 const 关键字
7.1 #define 预处理器
面是使用 #define 预处理器定义常量的形式:
#define identifier value
#include <iostream>
using namespace std;#define LENGTH 10
#define WIDTH 5
#define NEWLINE '\n'int main()
{int area; area = LENGTH * WIDTH;cout << area;cout << NEWLINE;return 0;
}
50
7.2 const 关键字
您可以使用 const 前缀声明指定类型的常量,如下所示:
const type variable = value;
#include <iostream>
using namespace std;int main()
{const int LENGTH = 10;const int WIDTH = 5;const char NEWLINE = '\n';int area; area = LENGTH * WIDTH;cout << area;cout << NEWLINE;return 0;
}
50
菜鸟教程,学习记录
相关文章:

C++基础了解-05-C++常量
C常量 一、C常量 常量是固定值,在程序执行期间不会改变。这些固定的值,又叫做字面量。 常量可以是任何的基本数据类型,可分为整型数字、浮点数字、字符、字符串和布尔值。 常量就像是常规的变量,只不过常量的值在定义后不能进…...

深度学习笔记-2.自动梯度问题
通过反向传播进行自动求梯度1-requires_grad问题2-梯度3- detach() 和 with torch.no_grad()4- Tensor.data.requires_gradPyTorch提供的autograd包能够根据输入和前向传播过程自动构建计算图,并执行反向传播. 1-requires_grad问题 requires_gradTrue …...
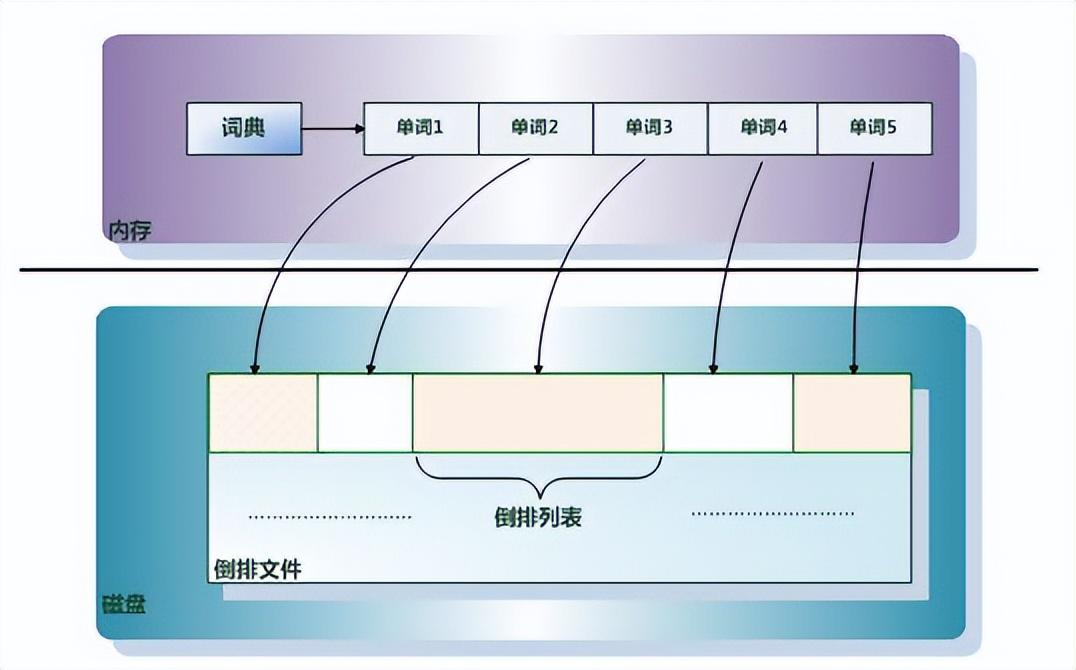
一文读懂倒排序索引涉及的核心概念
基础概念相信对于第一次接触Elasticsearch的同学来说,最难理解的概念就是倒排序索引(也叫反向索引),因为这个概念跟我们之前在传统关系型数据库中的索引概念是完全不同的!在这里我就重点给大家介绍一下倒排序索引&…...

Java基础算法题
以创作之名致敬节日 胜固欣然,败亦可喜。 --苏轼 目录 练习1 : 优化代码 扩展 : CRTL Alt M 自动抽取方法 练习2: 方法一: 方法二: 方法三: Math : 顾名思义,Math类就是用来进行数学计算的,它提供了大量的静态方法来便于我们实…...

「SAP ABAP」你真的了解OPEN SQL的DML语句吗 (附超详细案例讲解)
💂作者简介: THUNDER王,一名热爱财税和SAP ABAP编程以及热爱分享的博主。目前于江西师范大学本科在读,同时任汉硕云(广东)科技有限公司ABAP开发顾问。在学习工作中,我通常使用偏后端的开发语言A…...
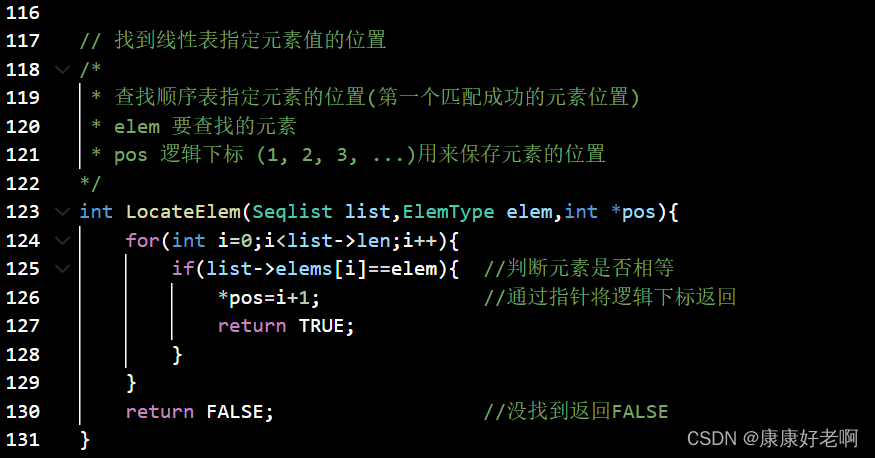
数据结构3——线性表2:线性表的顺序结构
顺序结构的基本理解 定义: 把逻辑上相邻的数据元素存储在物理上相邻(占用一片连续的存储单元,中间不能空出来)的存储单元的存储结构 存储位置计算: LOC(a(i1))LOC(a(i))lLOC(a(i1))LOC(a(i))l LOC(a(i1))LOC(a(i))l L…...
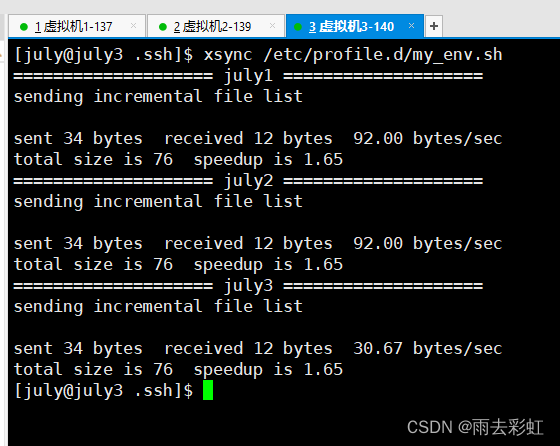
VMware虚拟机搭建环境通用方法
目录一、前期准备1.下载并安装一个虚拟机软件二、开始创建虚拟机1.配置虚拟机硬件相关操作2.虚拟机网络相关操作三、开机配置相关内容0.开机遇到报错处理(选看--开机没有报错请忽略)1.开始配置2.开机之后配置3.使用xshell远程登录4.使用xshell配置虚拟机…...

2.Fully Convolutional Networks for Semantic Segmentation论文记录
欢迎访问个人网络日志🌹🌹知行空间🌹🌹 文章目录1.基础介绍2.分类网络转换成全卷积分割网络3.转置卷积进行上采样4.特征融合5.一个pytorch源码实现参考资料1.基础介绍 论文:Fully Convolutional Networks for Semantic Segmentati…...

深度解析Spring Boot自动装配原理
废话不多说了,直接来看源码。源码解析SpringBootApplication我们在使用idea创建好Spring Boot项目时,会发现在启动类上添加了SpringBootApplication注解,这个注解就是Spring Boot的核心所在。点击注解可以查看到到它的实现ementType.TYPE) Re…...

Linux:环境变量
目录一、环境变量的理解(1)什么是环境变量?(2)Linux中的环境变量二、环境变量的使用(1)PATH环境变量(2)和变量相关的指令三、环境变量与普通变量的区别在平时使用电脑的时…...

Codeforces Round 703 (Div. 2)(A~D)
A. Shifting Stacks给出一个数组,每次可以将一个位置-1,右侧相邻位置1,判断是否可以经过若干次操作后使得数列严格递增。思路:对于每个位置,前缀和必须都大于该位置应该有的最少数字,即第一个位置最少是0&a…...

Django项目5——基于tensorflow serving部署深度模型——windows版本
1:安装docker for windows 可能需要安装WLS2,用于支持Linux系统,参照上面的教程安装 2:在Powershell下使用docker docker pull tensorflow/serving3:在Powershell下启动tensorflow serving docker run -p 8500:8500 …...
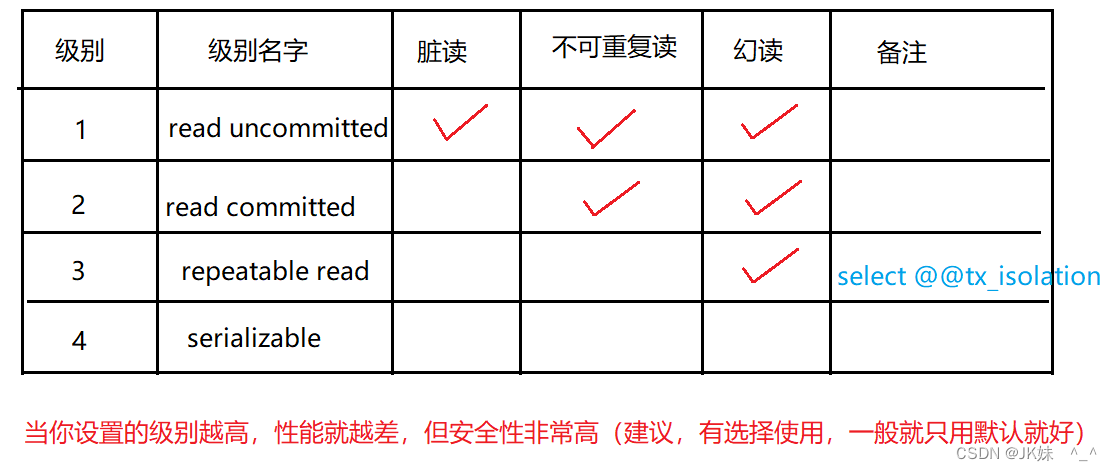
MySQL基础篇3
第一章 多表关系实战 1.1 实战1:省和市 方案1:多张表,一对多 方案2:一张表,自关联一对多 id1 name‘北京’ p_id null; id2 name‘昌平’ p_id1 id3 name‘大兴’ p_id1 id3 name‘上海’ p_idnull id4 name‘浦东’…...
携程 x TiDB丨应对全球业务海量数据增长,一栈式 HTAP 实现架构革新
随着新冠病毒疫情的缓解和控制,全球旅游业逐渐开始重新复苏。尤其在一些度假胜地,游客数量已经恢复到疫情前的水平。 携程作为全球领先的一站式旅行平台,旗下拥有携程旅行网、去哪儿网、Skyscanner 等品牌。携程旅行网向超过 9000 万会员提供…...

记一次Kafka warning排查过程
1、前因 在配合测试某个需求的时候,正好看到控制台打印了个报错,如下: 2023-03-06 17:05:58,565[325651ms][pool-28-thread-1][org.apache.kafka.common.utils.AppInfoParser][WARN] - Error registering AppInfo mbean javax.management.I…...
)
MySQL学习笔记(6.视图)
1. 视图作用 (1). 简化业务,将多个复杂条件,改为视图 (2). mysql对用户授权,只能控制表权限,通过视图可以控制用户字段权限。 (3). 可以避免基本表变更,影响业务。只需更改视图即可。 2. 视图(创建&…...

java多线程与线程池-01多线程知识复习
多线程知识复习 文章目录 多线程知识复习第1章 多线程基础1.1.2 线程与进程的关系1.2 多线程启动1.2.1 线程标识1.2.2 Thread与Runnable1.2.3 run()与start()1.2.4 Thread源码分析1.3 线程状态1.3.1 NEW状态1.3.2 RUNNABLE状态1.3.3 BLOCKED状态1.3.4 WAITING状态1…...

Typescript - 将命名空间A导入另一个命名空间B作为B的子命名空间,并全局暴露命名空间B
前言 最近相统一管理 ts 中的类型声明,这就需要将各模块下的命名空间整合到全局的命名空间下,牵涉到从别的文件中引入命名空间并作为子命名空间在全局命名空间中统一暴露。 将命名空间A导入另一个命名空间B作为B的子命名空间 文件说明 assets.ts 文件中…...
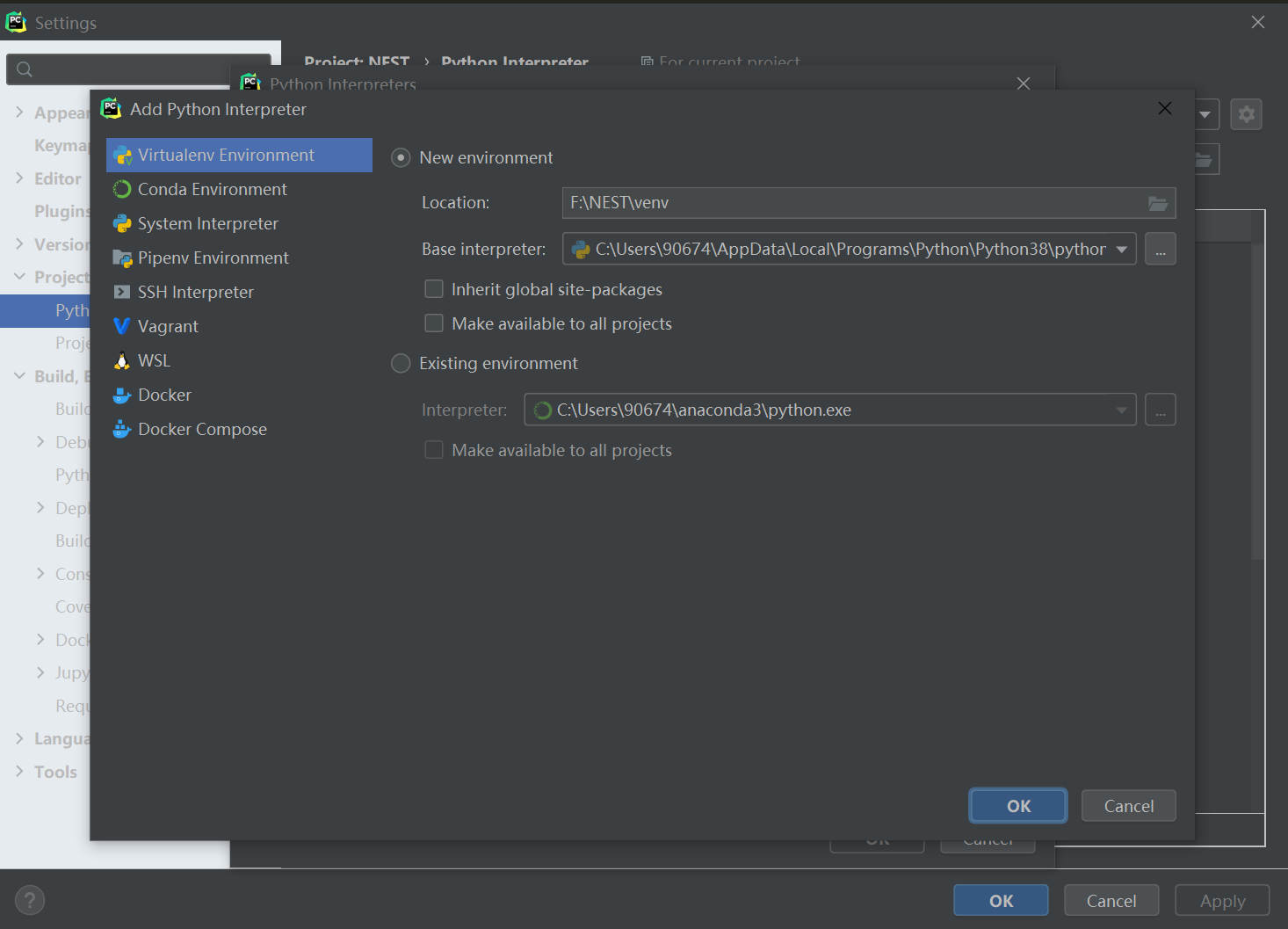
Windows下实现Linux内核的Python开发(WSL2+Conda+Pycharm)
许多软件可以通过Python交互,但没有开发Windows版本,这个时候装双系统或虚拟机都很不方便,可以采取WSL2CondaPycharm的策略来进行基于Linux内核的Python开发。启动WSL2,安装Linux内核教程:旧版 WSL 的手动安装步骤 | M…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
)
.Net Framework 4/C# 关键字(非常用,持续更新...)
一、is 关键字 is 关键字用于检查对象是否于给定类型兼容,如果兼容将返回 true,如果不兼容则返回 false,在进行类型转换前,可以先使用 is 关键字判断对象是否与指定类型兼容,如果兼容才进行转换,这样的转换是安全的。 例如有:首先创建一个字符串对象,然后将字符串对象隐…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

基于IDIG-GAN的小样本电机轴承故障诊断
目录 🔍 核心问题 一、IDIG-GAN模型原理 1. 整体架构 2. 核心创新点 (1) 梯度归一化(Gradient Normalization) (2) 判别器梯度间隙正则化(Discriminator Gradient Gap Regularization) (3) 自注意力机制(Self-Attention) 3. 完整损失函数 二…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...
零知开源——STM32F103RBT6驱动 ICM20948 九轴传感器及 vofa + 上位机可视化教程
STM32F1 本教程使用零知标准板(STM32F103RBT6)通过I2C驱动ICM20948九轴传感器,实现姿态解算,并通过串口将数据实时发送至VOFA上位机进行3D可视化。代码基于开源库修改优化,适合嵌入式及物联网开发者。在基础驱动上新增…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

Vue3 PC端 UI组件库我更推荐Naive UI
一、Vue3生态现状与UI库选择的重要性 随着Vue3的稳定发布和Composition API的广泛采用,前端开发者面临着UI组件库的重新选择。一个好的UI库不仅能提升开发效率,还能确保项目的长期可维护性。本文将对比三大主流Vue3 UI库(Naive UI、Element …...

