数据结构与算法笔记:基础篇 - 栈:如何实现浏览器的前进和后退功能?
概述
浏览器的前进、后退功能,你肯定很熟悉吧?
当依次访问完一串页面 a-b-c 之后,点击浏览器的后退按钮,就可以查看之前浏览过的页面 b 和 a。当后退到页面 a,点击前进按钮,就可以重新查看页面 b 和 c。但是,如果你后退到页面 b 后,点击新的页面 d,那就无法再通过前进、后退功能查看页面 c 了。
假设你是浏览器的开发工程师,你会如何实现这个功能呢?
这就要用到本章讲的 “栈” 这种数据结构了。
如何理解 “栈”?
关于 “栈”,有一个非常贴切的例子,就是一摞叠在一起的盘子。我们平时放盘子时,都是从下往上一个一个的放;取的时候,也是从上往下一个一个地依次取,不能从中间任意抽出。后进者先出,先进者后出,这就是典型的 “栈” 结构。
从栈的操作特性上来看,栈是一种 “操作受限” 的线性表,只允许在一端插入和删除数据。
第一次接触这种数据类型时,我对它存在的意义产生了很大的疑惑。因为我觉得,相比数组和链表,栈给我的只有限制,并没有任何优势。那我直接使用数组或链表不就好了吗?为什么还要用这个 “操作受限” 的 “栈” 呢?
事实上,从功能上来说,数组或链表确实可以替代栈,但你要知道,特定的数据结构是对特定场景的抽象,而且,数组或链表暴露了太多的接口,操作上的确灵活,但使用时就比较不可控,自然也就容易出错。
当某个数据集合只涉及在一端插入和删除数据,并且满足后进先出、先进后出的特性,这是应该首选 “栈” 这种数据结构。
如何实现一个 “栈”?
从刚才栈的定义里,我们可以看出,栈主要包含两个操作,入栈和出栈,也就是在栈顶插入一个数据和从栈顶删除一个数据。理解了栈的定义后,我们来看下如何用代码实现一个栈。
实际上,栈既可以用数组来实现,也可以用链表来实现。
- 用数组实现的栈,我们叫做顺序栈。
- 用链表实现的栈,我们叫做链式栈。
这里实现一个基于数组的顺序栈。
这段代码使用 Java 来实现,但不涉及任何高级语法,并且用了中文做了详细的注释。
public class ArrayStack {private String[] items; // 数组private int count; // 栈中元素个数private int n; // 栈大小public ArrayStack(int n) {this.items = new String[n];this.count = 0;this.n = n;}// 入栈操作public boolean push(String item) {if (count == n) {// 数组空间不够了,直接返回false,入栈失败return false;}items[count] = item;count++;return true;}// 出栈操作public String pop() {if (count == 0) {// 栈为空,直接返回nullreturn null;}// 返回下标为count-1的数组元素,并且栈中元素个数减1String temp = items[count - 1];count--;return temp;}
}
了解了定义和基本操作,那它的操作时间、框架复杂度时多少呢?
不管是顺序栈还是链式栈,存储数据只需要一个大小为 n 的数组就够了。在入栈和出栈的过程中,只需要一两个临时变量存储空间,所以空间复杂度时 O ( 1 ) O(1) O(1)。
注意,这里存储数据需要一个大小为 n 的数组,并不是说空间复杂度就是 O ( n ) O(n) O(n)。因为,这 n 个空间是必须的,无法省掉。所以我们说空间复杂度的时候,是除了原本的数据存储空间外,算法运行还需要额外的存储空间。
框架复杂度分析是不是很简单?时间复杂度也不难。不管是顺序栈还是链式栈,入栈、出栈只涉及栈顶个人数据的操作,所以时间复杂度都是 O ( 1 ) O(1) O(1)。
支持动态扩容的顺序栈
刚才那个基于数组实现的栈,是一个固定大小的栈,也就是说,在初始化栈时需要实现制定栈的大小。当栈满之后,就无法再往栈里添加数据了。尽管链式栈的大小不受限,但要存储 next 指针,内存消耗相对较多。那我们如何基于数组实现一个可以支持动态扩容的栈呢?
还记得在数组那篇文章,是如何来支持一个支持动态扩容的数组吗?当数组空间不够时,我们就重新申请一块更大的内存,将原来数组中的数据统统拷贝过去。这样就实现了一个支持动态扩容的数组。
所以,如果要实现一个支持动态扩容的栈,我们只需要底层依赖一个支持动态扩容的数组就可以了。当栈满了之后,我们就申请一个更大的数组,将原来的数据搬移到新数组中。
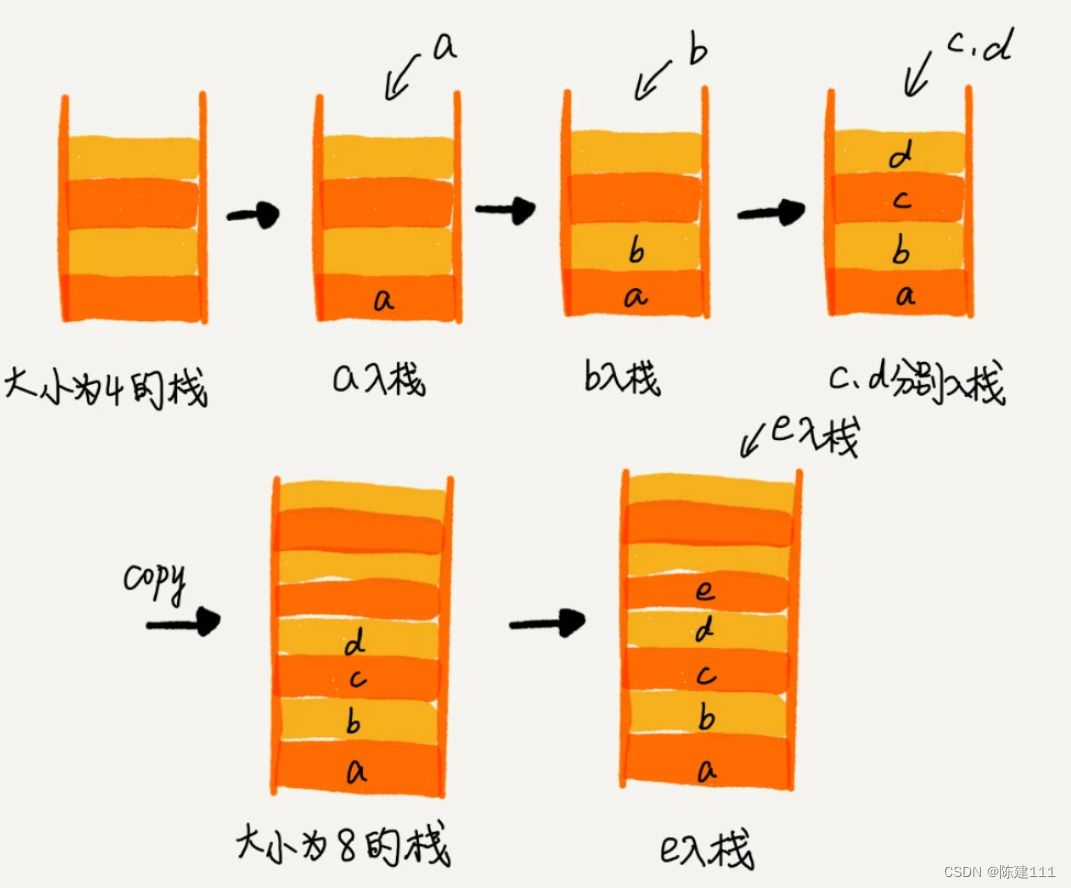
实际上,支持动态扩容的顺序栈,我们平时开发中并不常用到。讲这个的目的,主要还是希望带你练习一下前面将的复杂度分析方法。
你不用死记硬背入栈、出栈的时间复杂度,你需要掌握的是分析方法。能够自己分析才算是真正掌握了。现在就带你一起分析一下支持动态扩容的顺序栈的入栈、出栈的时间复杂度。
对于出栈操作来说,我们不会涉及内存的重新申请和数据搬移,所以出栈的时间复杂度还是 O ( 1 ) O(1) O(1)。但是对于入栈来说,当占用有空闲空间时,入栈操作的时间复杂度是 O ( 1 ) O(1) O(1)。但当空间不够时,就需要申请内存和数据搬移,所以时间复杂度编程了 O ( n ) O(n) O(n)。
也就是说,对于入栈操作,最好情况时间复杂度是 O ( 1 ) O(1) O(1),最坏情况时间复杂度是 O ( n ) O(n) O(n)。那平均情况下的时间复杂度又是多少呢?还记得我们在复杂度那篇文章中讲的摊还分析法吗?这个入栈操作的平均时间复杂度可以用摊还分析法来分析。正好也借此再回顾一下摊还分析法。
为了分析的方便,我们需要预先做一些假设和定义:
- 栈空间不够时,我们重新申请一个原来大小两倍的数组;
- 为了简化分析,假设只有入栈操作没有出栈操作;
- 定义不涉及内存搬移的入栈操作为
simple-push,时间复杂度为 O ( 1 ) O(1) O(1)。
如果当前栈大小为 k,并且已满,当再有新的数据要入栈时,就需要重新申请 2 倍大小的内存,并且做 k 个数据的搬移操作,然后再入栈。
- 我们将
k个数据的搬移操作,均摊到前面 k 次的simple-push操作。 - 均摊后,每个入栈只需要一次
simple-push操作和 一次搬移操作。 - 也就是说,均摊后,入栈操作的均摊时间复杂度就为 O ( 1 ) O(1) O(1)。
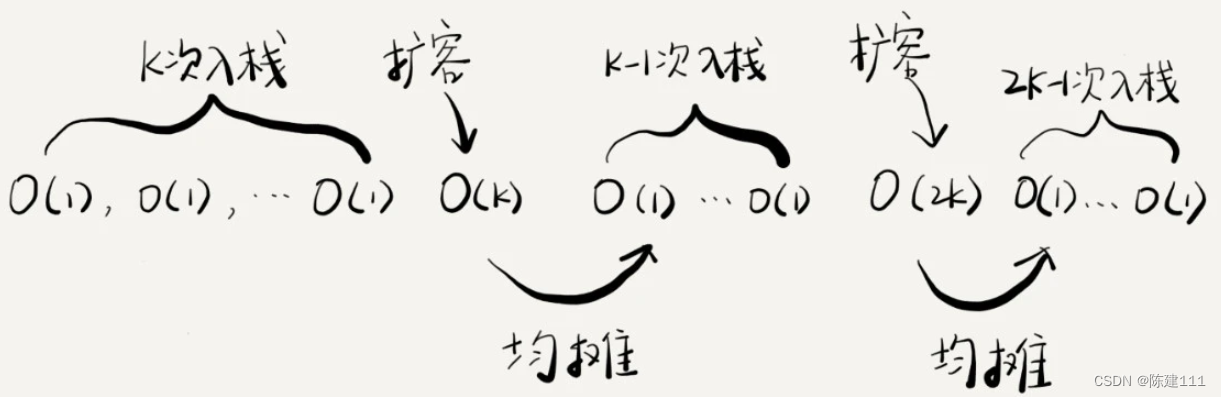
通过这个例子的实战分析,也印制了前面讲的,均摊时间复杂度一般都等于最好情况时间复杂度。因为在大部分情况下,入栈的操作时间复杂度都是 O ( 1 ) O(1) O(1),只有在个别时刻才会退化为 O ( n ) O(n) O(n),所以把好是多的入栈操作均摊到其他入栈操作上,平均情况下的耗时就接近 O ( 1 ) O(1) O(1)。
栈在函数调用中的应用
接下来在看栈的另一个常见的应用场景,编译器如何利用栈来实现表达式求值。
为了方便解释,我们将算术表达式简化为只包含加减乘除四则运算,比如:34+13*9+44-12/3。对于这个四则运算,人脑可以很快求接触答案,但是对于计算机来说,理解这个表达式本身就是个挺难得事儿。如果换作你,让你来实现这样一个表达式求值的功能,你会怎么做?
实际上,编译器就是通过两个栈来实现的。其中一个是保存操作数的栈,另一个是保存运算符的栈。我们从左向右遍历表达式:
- 当遇到数字,我们就直接压入操作数栈;
- 当遇到运算符,就与运算符栈的栈顶元素进行比较。
- 如果运算符 比 运算符栈顶元素的优先级高,就将当前的运算符压入栈;
- 如果运算符 比 运算符栈顶元素的优先级低或者相同,从运算符中取栈顶运算符,从操作数栈的栈顶取 2 个操作数,然后进行计算,再把计算的记过压入操作数栈,继续比较。
我们将 3+5*8-6 这个表达式的计算过程画了一张图,你可以 结合图来理解上面的计算过程。
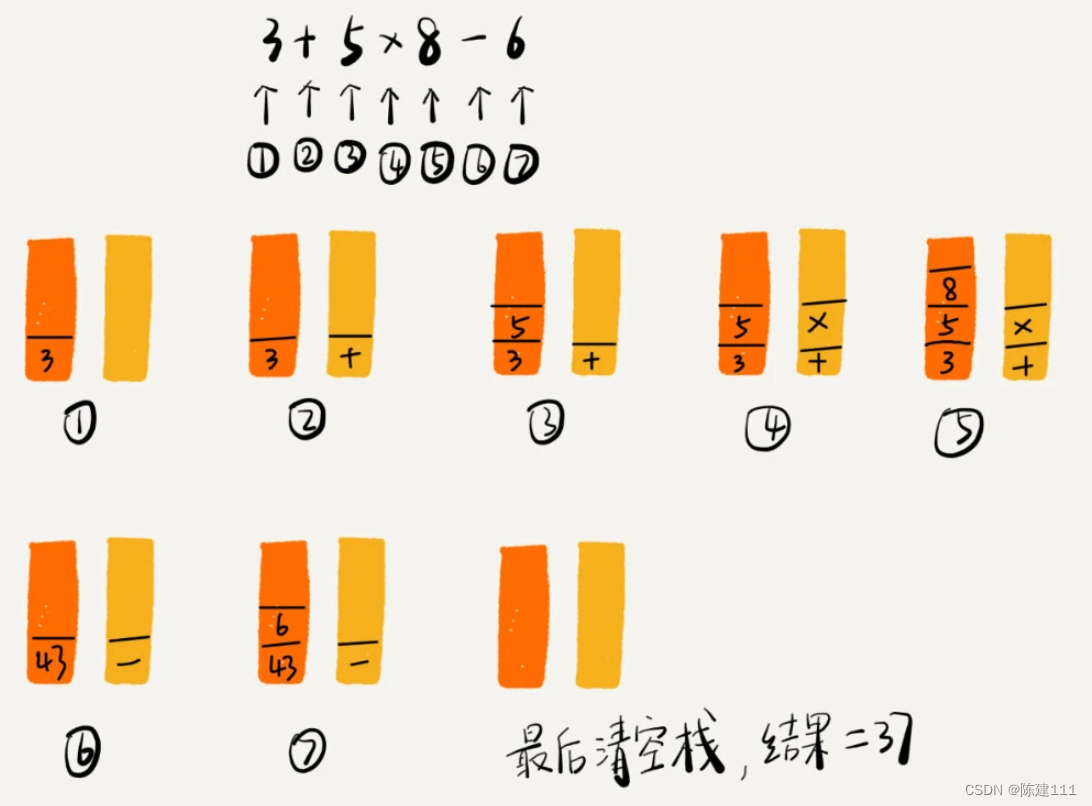
栈在括号匹配中的应用
除了用栈来实现表达式求值,还可以借助栈来检查表达式中的括号匹配。
假设表达式中只包含三种括号,圆括号 ()、花括号 {} 和方括号 [],并且它们可以任意嵌套。比如 {[]()[{}]} 或 [{()}([])] 等都为合法格式,而 {[}()] 或 [({)] 问哦不合法格式。那我现在给你一个包含三种括号的表达式字符串,如何检查它们是否合法呢?
这里也可以使用栈来解决。用栈来保存未匹配的左括号,从左到右一次扫描字符串。当扫描到左括号时,将其压入栈中;当扫描到有括号时,从栈顶取出一个左括号。如果能够匹配,比如 ( 跟 ) 匹配,[ 跟 ] 匹配,{ 跟 } 匹配,则继续扫描剩下的字符串。如果扫描过程中,遇到不能匹配的右括号,或者栈中没有数据,则说明为非法格式。
当所有的括号都扫描完成之后,如果栈为空,则说明字符串为合法字符串;否则,说明有未匹配的左括号,为非法格式。
如何实现浏览器的前进、后退功能?
其实,用两个栈就可以完美解决。
我们使用两个栈,X 和 Y,我们把首次浏览的页面压入栈 X,当点击后退按钮时,再一次从栈 X 中出栈,并将出栈的数据依次放入栈 Y。当我们点击前进按钮时,依次从栈 Y 中取出数据,放入栈 X。当 X 中没有数据时,那就说明没有页面可以后退浏览了。当栈 Y 中没有数据,那就说明没有页面可以点击前进按钮浏览了。
比如,你顺序查看了 a,b,c 三个页面,我们依次把 a,b,c 压入栈 X,这个时候,两个栈的数据就是这个样子的。
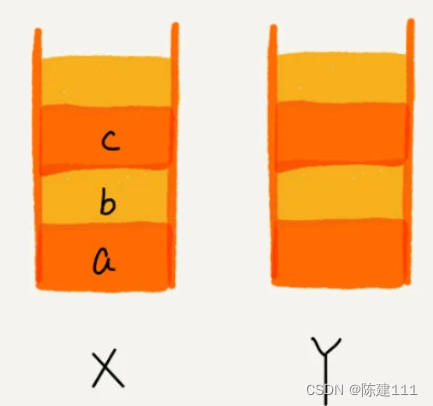
当你通过后退按钮,从页面 c 退到页面 a 之后,我们就一次把 c 和 b 从栈 X 中取出,并依次放入栈 Y。这个时候数据就是这样的。
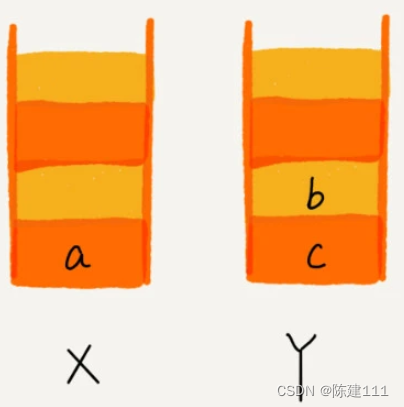
这个时候,如果你又想看页面 b,于是你点击了前进按钮回到页面 b,我们就再把 b 从栈 Y 出栈,放入栈 X。
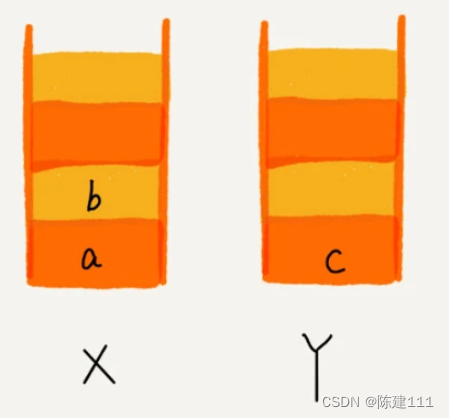
这个时候,你通过页面 b 跳转到新的页面 d,页面 c 就无法再通过前进、后退按钮重复查看了,所以需要清空栈 Y。
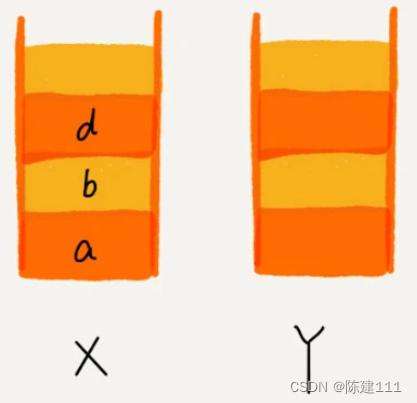
小结
栈是一种操作受限的数据结构,只支持入栈和出栈操作。后劲先出是它最大的特点。栈既可以通过数组实现,也可以通过链表来实现。不管基于数组还是链表,入栈、出栈的时间复杂度都为 O ( 1 ) O(1) O(1)。此外,还讲了一种支持动态扩容的顺序栈,你需要掌握其均摊时间复杂度的分析方法。
相关文章:

数据结构与算法笔记:基础篇 - 栈:如何实现浏览器的前进和后退功能?
概述 浏览器的前进、后退功能,你肯定很熟悉吧? 当依次访问完一串页面 a-b-c 之后,点击浏览器的后退按钮,就可以查看之前浏览过的页面 b 和 a。当后退到页面 a,点击前进按钮,就可以重新查看页面 b 和 c。但…...

【AIGC】大型语言模型在人工智能规划领域模型生成中的探索
大型语言模型在人工智能规划领域模型生成中的新应用 一、引言二、LLM在规划领域模型生成中的潜力三、实证分析:LLM在规划领域模型生成中的表现四、代码实例:LLM在规划领域模型生成中的应用五、结论与展望 一、引言 随着人工智能技术的迅猛发展࿰…...

从零开始学习Slam-旋转矩阵旋转向量四元组(二)
本文参考:计算机视觉life 仅作笔记用 书接上回,上回不清不楚的介绍了旋转矩阵&旋转向量和四元组 现在回顾一下重点: 本着绕谁谁不变的变则 假设绕z轴旋转θ,旋转矩阵为: 再回顾一下旋转向量的表示以及这个基本记不…...

基于Spring Security添加流控
基于Spring Security添加流控的过程: 步骤1: 添加依赖 确保项目中包含了Spring Security和Sentinel-Core的相关依赖。在Maven项目中,可以在pom.xml中添加如下依赖: <!-- Spring Security --> <dependency><groupId>org.…...
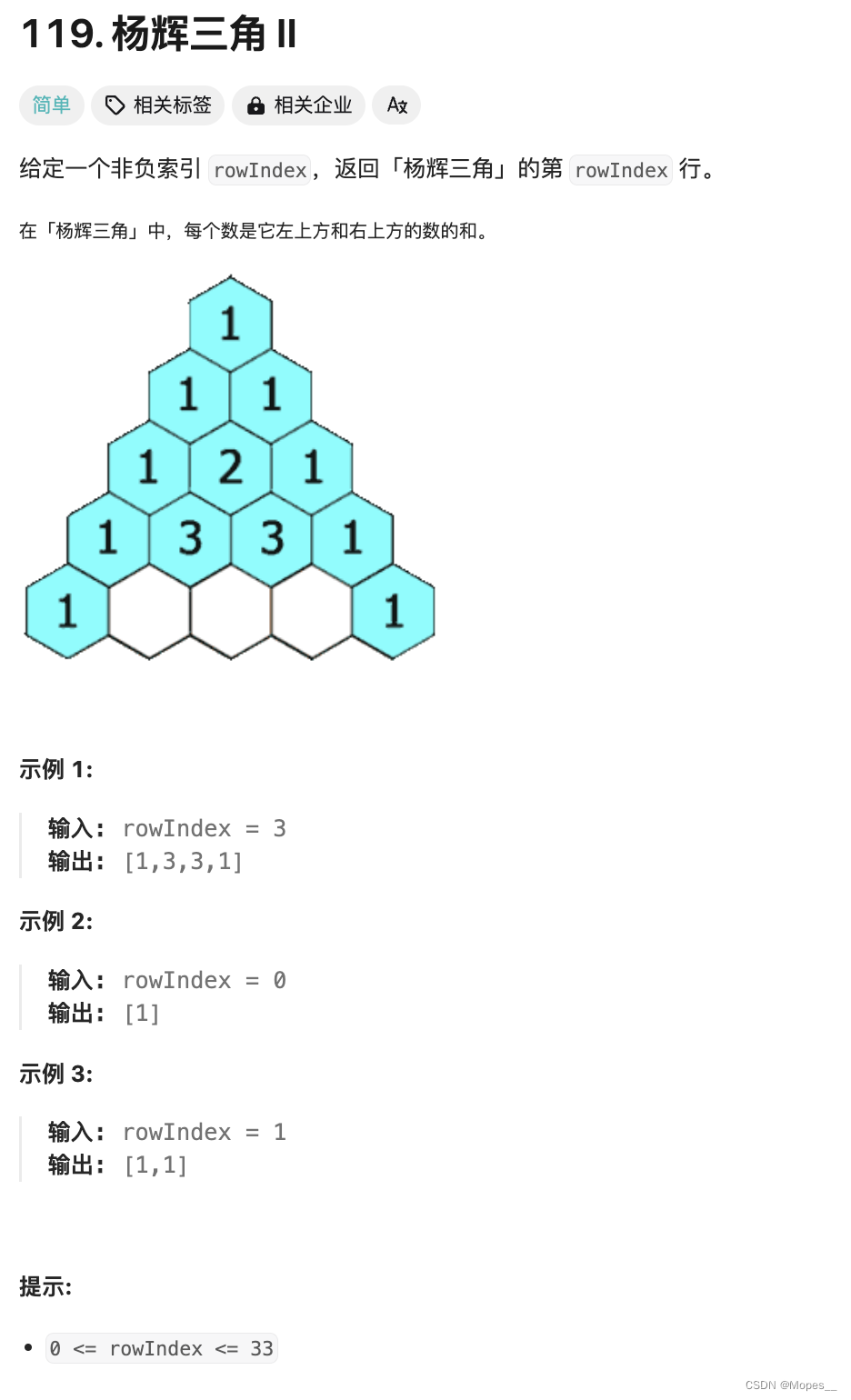
Python | Leetcode Python题解之第119题杨辉三角II
题目: 题解: class Solution:def getRow(self, rowIndex: int) -> List[int]:row [1, 1]if rowIndex < 1:return row[:rowIndex 1]elif rowIndex > 2:for i in range(rowIndex - 1):row [row[j] row[j 1] for j in range(i 1)]row.inser…...

物联网应用系统与网关
一. 传感器底板相关设计 1. 传感器设计 立创EDA传感器设计举例。 2. 传感器实物图 3. 传感器测试举例 测试激光测距传感器 二. 网关相关设计 1. LORA,NBIOT等设计 2. LORA,NBIOT等实物图 3. ZigBee测试 ZigBee测试 4. NBIoT测试 NBIoT自制模块的测试…...

系统稳定性概览
系统稳定性 系统稳定性,包括:监控、 告警、性能优化、慢sql、耗时接口等。 系统的稳定性的治理,可以围绕这几方面展开。 监控 Prometheus 监控并收集数据。监控 qps,tps, rt , cpu使用率,cpu load&#…...

Redis-Cluster模式基操篇
一、场景 1、搞一套6个主节点的Cluster集群 2、模拟数据正常读写 3、模拟单点故障 4、在不停服务的情况下将集群架构改为3主3从 二、环境规划 6台独立的服务器,端口18001~18006 192.169.14.121 192.169.14.122 192.169.14.123 192.169.14.124 192.169.14.125 192…...
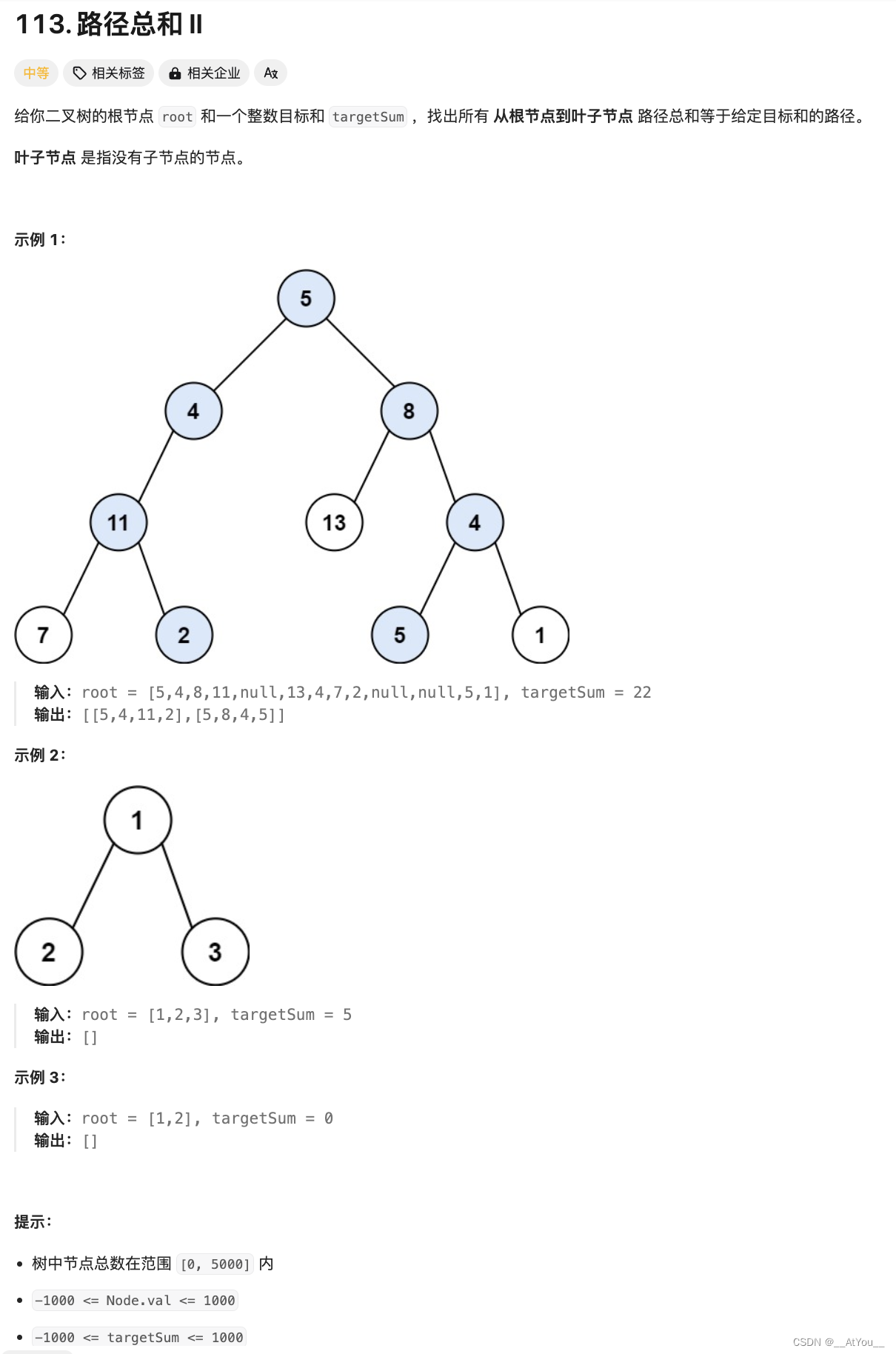
Golang | Leetcode Golang题解之第113题路径总和II
题目: 题解: type pair struct {node *TreeNodeleft int }func pathSum(root *TreeNode, targetSum int) (ans [][]int) {if root nil {return}parent : map[*TreeNode]*TreeNode{}getPath : func(node *TreeNode) (path []int) {for ; node ! nil; no…...
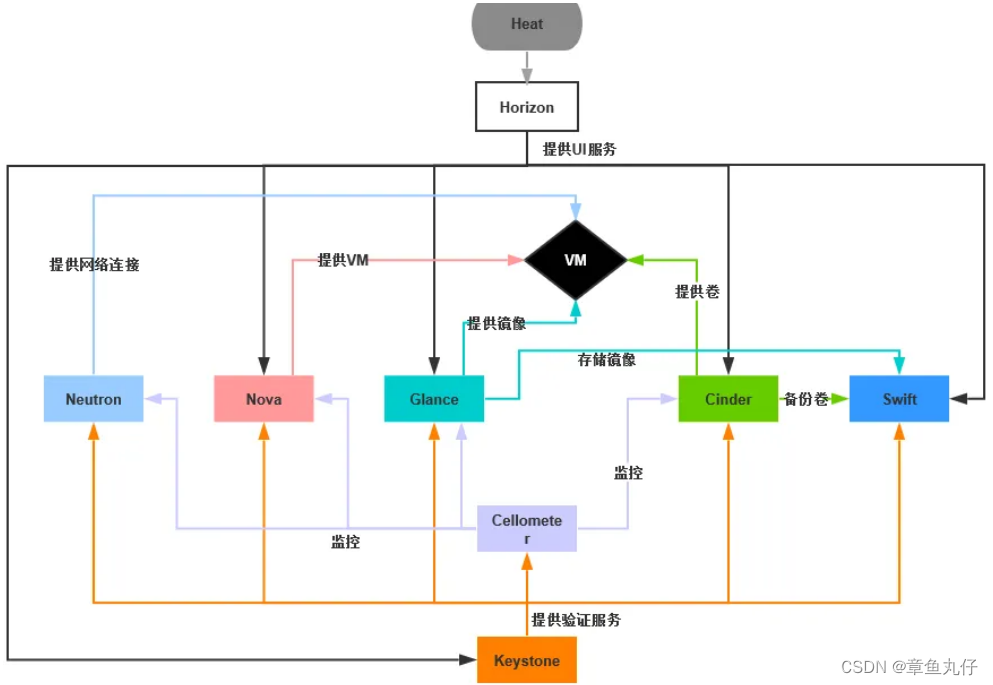
云计算与 openstack
文章目录 一、 虚拟化二、云计算2.1 IT系统架构的发展2.2 云计算2.3 云计算的服务类型 三、Openstack3.1 OpenStack核心组件 一、 虚拟化 虚拟化使得在一台物理的服务器上可以跑多台虚拟机,虚拟机共享物理机的 CPU、内存、IO 硬件资源,但逻辑上虚拟机之…...
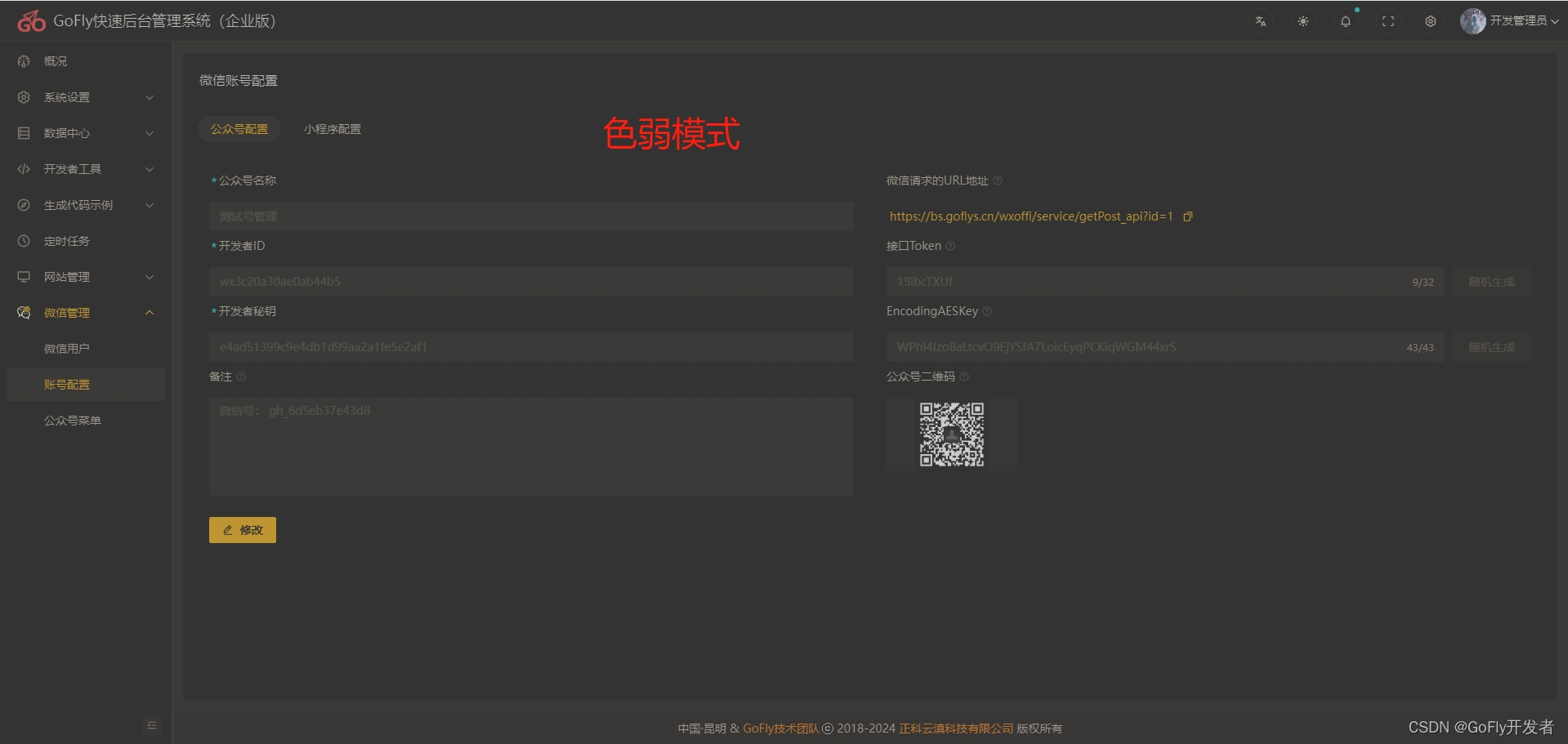
golang语言的gofly快速开发框架如何设置多样的主题说明
本节教大家如何用gofly快速开发框架后台内置设置参数,配置出合适项目的布局及样式、主题色,让你您的项目在交互上加分,也是能帮你在交付项目时更容易得到客户认可,你的软件使用客户他们一般都是不都技术的,所以当他们拿…...
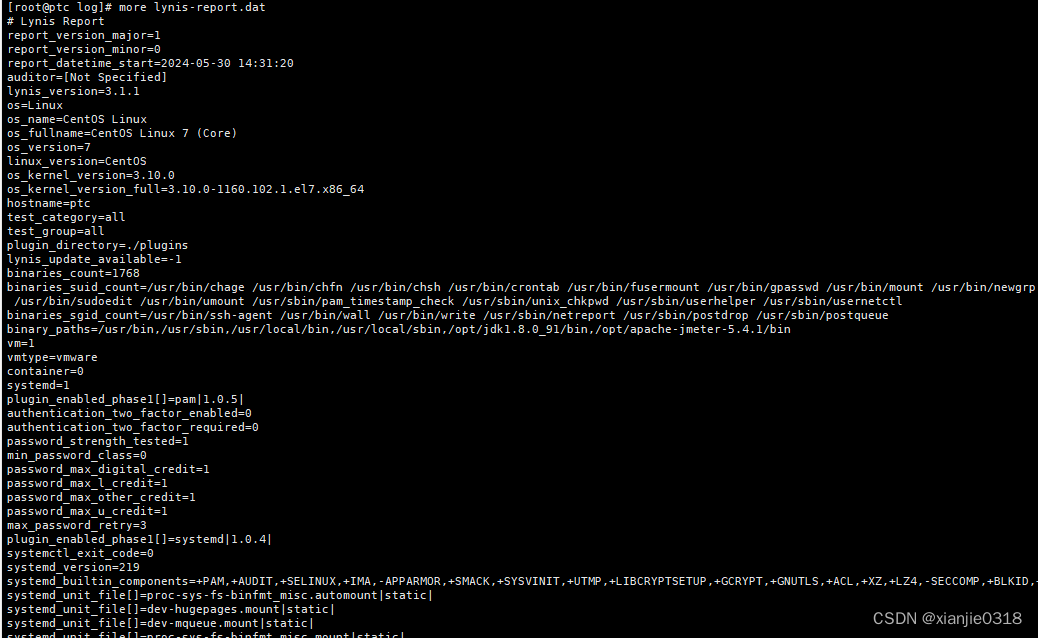
lynis安全漏洞扫描工具
Lynis是一款Unix系统的安全审计以及加固工具,能够进行深层次的安全扫描,其目的是检测潜在的时间并对未来的系统加固提供建议。这款软件会扫描一般系统信息,脆弱软件包以及潜在的错误配置。 安装 方式1 git下载使用git clone https://github…...
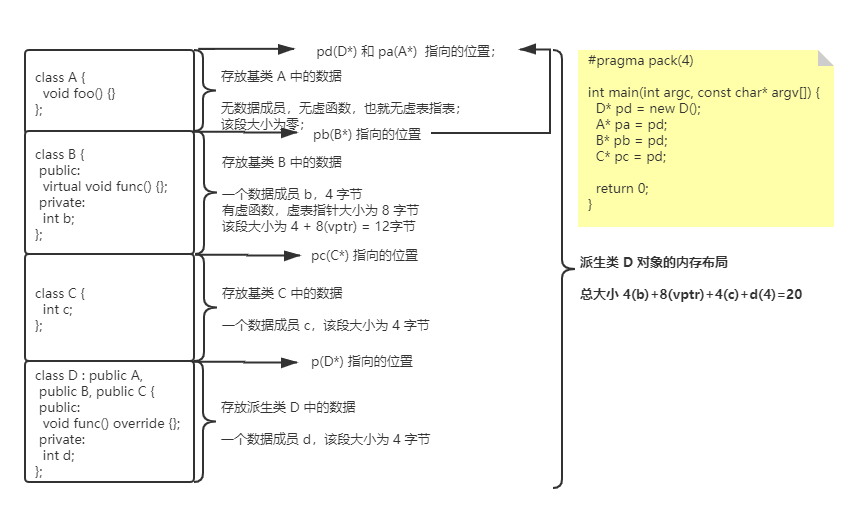
C++ 多重继承的内存布局和指针偏移
在 C 程序里,在有多重继承的类里面。指向派生类对象的基类指针,其实是指向了派生类对象里面,该基类对象的起始位置,该位置相对于派生类对象可能有偏移。偏移的大小,等于派生类的继承顺序表里面,排在该类前面…...

centos时间不对
检查当前时区是否正确 timedatectl status如果时区不正确,使用以下命令设置正确的时区(将Asia/Shanghai替换为您所在的时区): timedatectl set-timezone Asia/Shanghai如果时区正确但时间不准确,使用以下命令同步网络…...

通过Redis实现防止接口重复提交功能
本功能是在切面执行链基础上实现的功能,如果不知道切面执行链的同学,请看一下我之前专门介绍切面执行链的文章。 在SpringBoot项目中实现切面执行链功能-CSDN博客 1.定义防重复提交handler /*** 重复提交handler**/ AspectHandlerOrder public class …...

如何构建最小堆?
方式1:上浮调整 /*** 上浮调整(小的上浮)*/ public static void smallUp1(int[] arr, int child) {int parent (child - 1) / 2;while (0 < child && arr[child] < arr[parent]) { // 0 < child说明这个节点还是叶子arr[child] arr[child] ^ ar…...
客户端)
基于Netty实现安全认证的WebSocket(wss)客户端
1.Netty服务端 服务端代码参考【基于Netty实现安全认证的WebSocket(wss)服务端-CSDN博客】 2.Netty客户端 客户端代码参考【基于Netty实现WebSocket客户端-CSDN博客】中两种都可以;这里用的是第一种。 新增SslHandler的代码: …...
代码随想录算法训练营第四十四天 | 01背包问题 二维、 01背包问题 一维、416. 分割等和子集
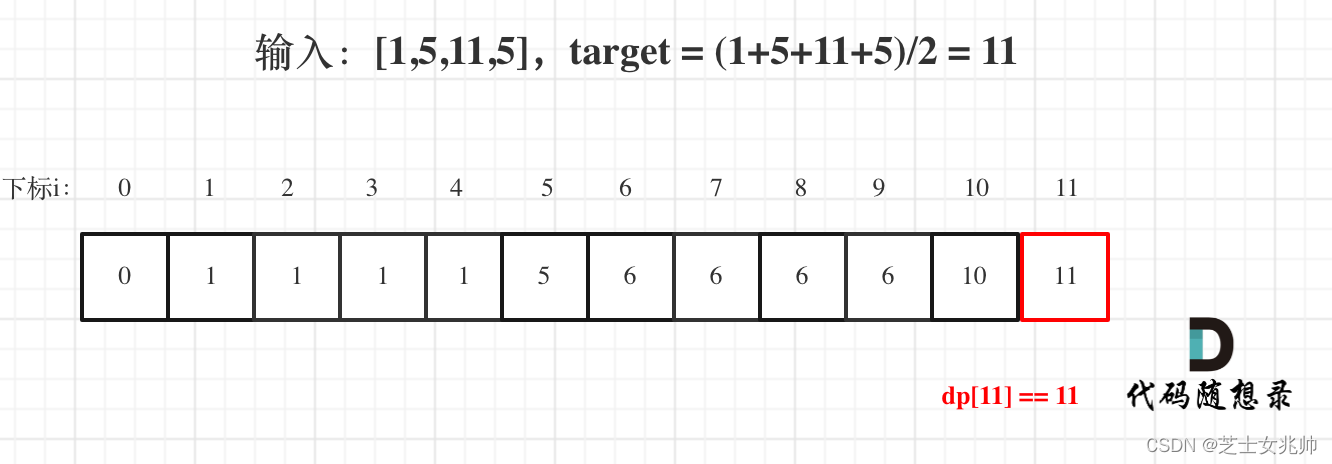
01背包问题 二维 代码随想录 视频讲解:带你学透0-1背包问题!| 关于背包问题,你不清楚的地方,这里都讲了!| 动态规划经典问题 | 数据结构与算法_哔哩哔哩_bilibili 1.dp数组定义 dp[i][j] 下标为[0,i]之间的物品&…...

redis常见使用场景
文章目录 redis常见使用场景全局ID位统计购物车用户消息时间线timeline抽奖商品筛选分布式锁限流redis实现计数器排行榜消息队列redis 如何实现延时队列 redis生产常用的场景 redis常见使用场景 Redis 是一种高性能的内存数据库,广泛应用于各种场景中。以下是 Redi…...
算法更新公式推导)
模糊C均值(FCM)算法更新公式推导
模糊C均值(FCM)算法更新公式推导 目标函数 FCM的目标函数为: J m ∑ i 1 n ∑ j 1 k u i j m ∥ x i − c j ∥ 2 J_m \sum_{i1}^n \sum_{j1}^k u_{ij}^m \|x_i - c_j\|^2 Jmi1∑nj1∑kuijm∥xi−cj∥2 其中: …...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

YSYX学习记录(八)
C语言,练习0: 先创建一个文件夹,我用的是物理机: 安装build-essential 练习1: 我注释掉了 #include <stdio.h> 出现下面错误 在你的文本编辑器中打开ex1文件,随机修改或删除一部分,之后…...

Java - Mysql数据类型对应
Mysql数据类型java数据类型备注整型INT/INTEGERint / java.lang.Integer–BIGINTlong/java.lang.Long–––浮点型FLOATfloat/java.lang.FloatDOUBLEdouble/java.lang.Double–DECIMAL/NUMERICjava.math.BigDecimal字符串型CHARjava.lang.String固定长度字符串VARCHARjava.lang…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

第一篇:Agent2Agent (A2A) 协议——协作式人工智能的黎明
AI 领域的快速发展正在催生一个新时代,智能代理(agents)不再是孤立的个体,而是能够像一个数字团队一样协作。然而,当前 AI 生态系统的碎片化阻碍了这一愿景的实现,导致了“AI 巴别塔问题”——不同代理之间…...

linux 下常用变更-8
1、删除普通用户 查询用户初始UID和GIDls -l /home/ ###家目录中查看UID cat /etc/group ###此文件查看GID删除用户1.编辑文件 /etc/passwd 找到对应的行,YW343:x:0:0::/home/YW343:/bin/bash 2.将标红的位置修改为用户对应初始UID和GID: YW3…...
