常用中间件各版本下载
常用中间件下载地址
- 前言
- 分布式中间件
- 负载均衡中间件
- 缓存中间件
- 数据库中间件
- 其他中间件
- 1、Maven下载地址
- 2、Git下载地址
- 2、JDK下载地址
- 3、MySQL下载地址
- 4、Redis下载地址
- 5、Nacos下载地址
- 6、Tomcat下载地址
- 7、Nginx下载地址
- 8、RocketMQ下载地址
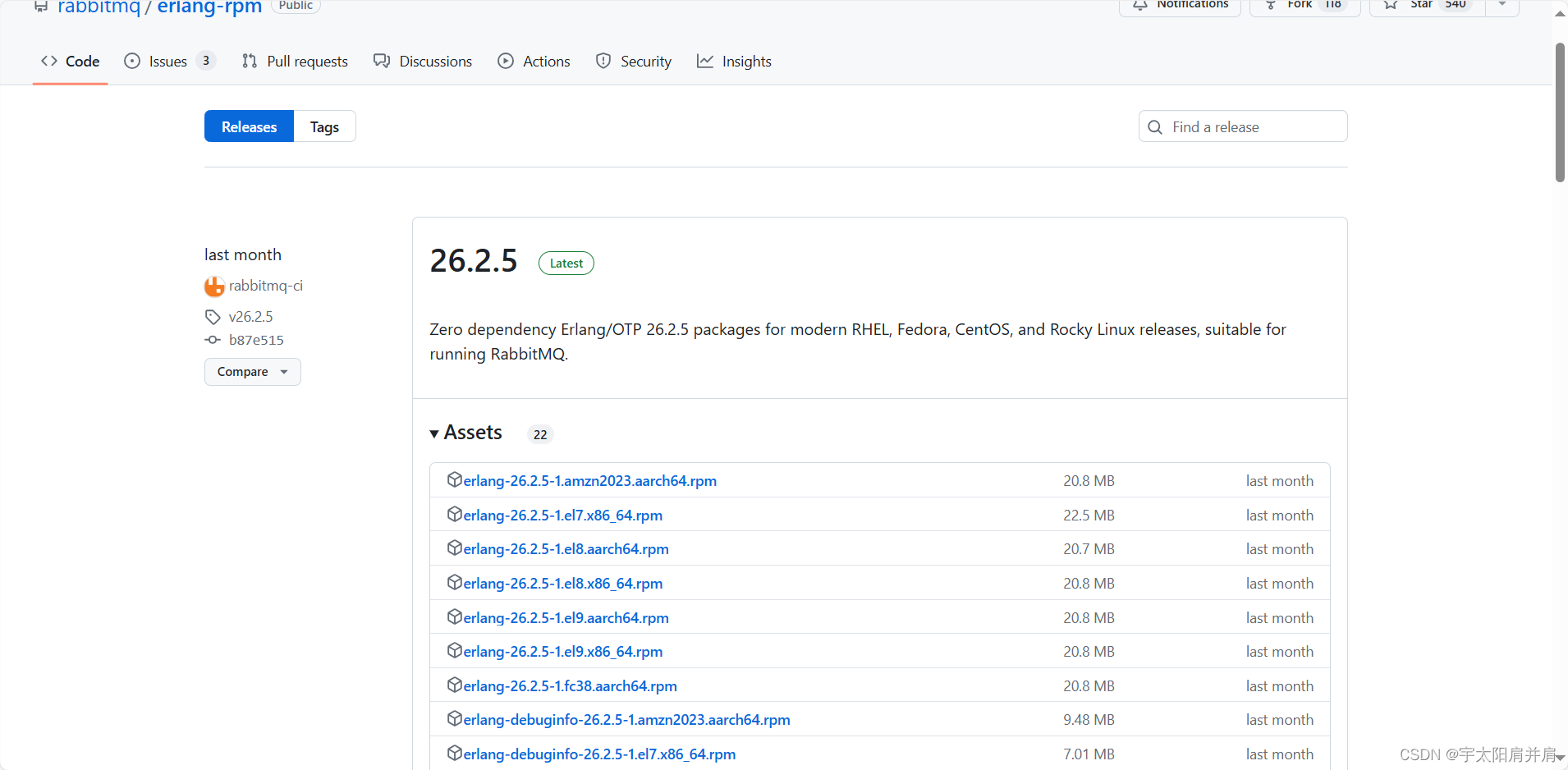
- 8、RabbitMQ下载地址
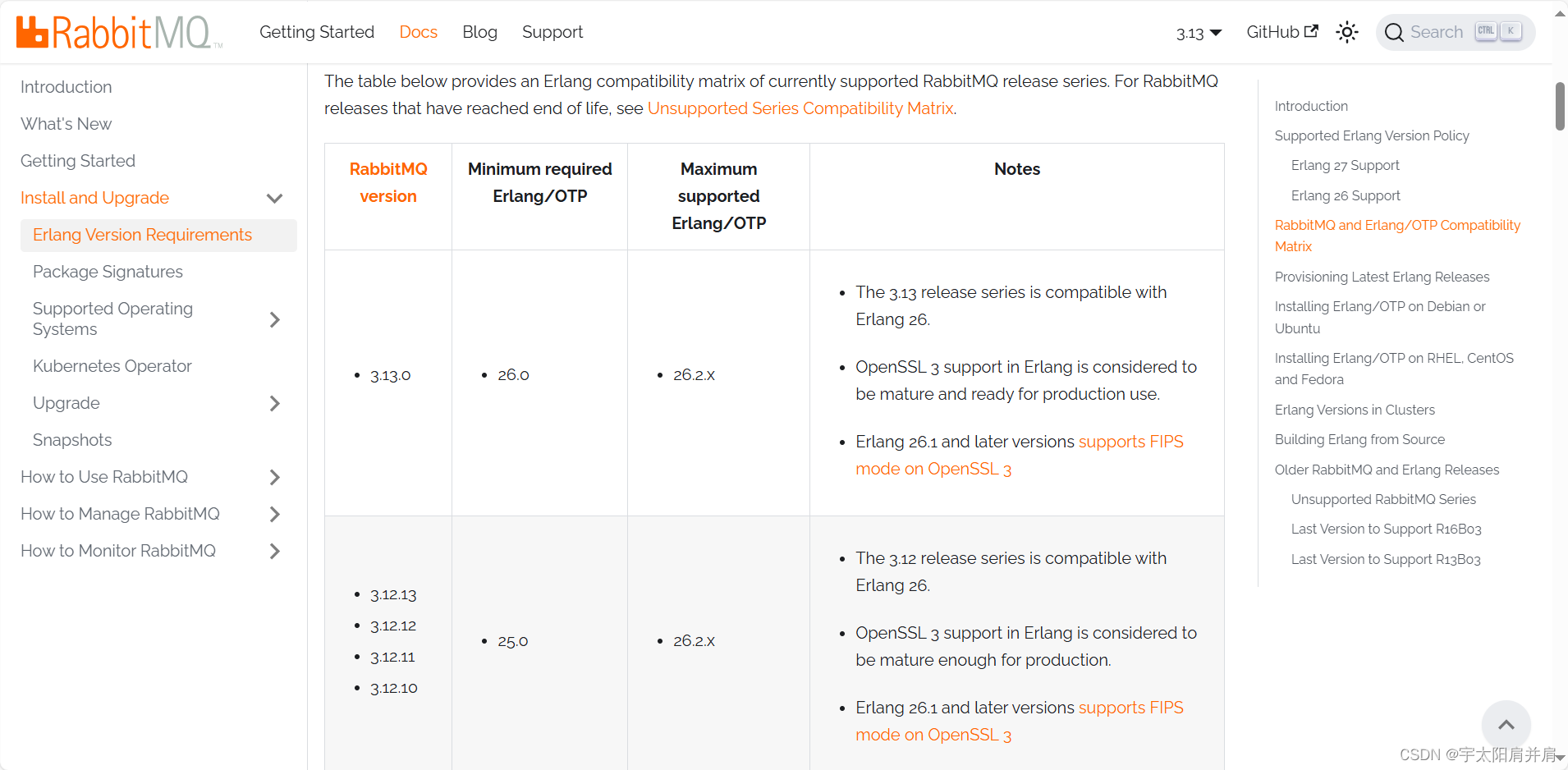
- 8、Erlang下载地址
前言
本篇只作为工作中常用的各中间件的各种版本下载地址收集展示使用,不要随便使用来历不明的安装包。
本篇中所有下载地址皆为官方链接或合作方链接,可放心食用。
分布式中间件
负载均衡中间件
缓存中间件
数据库中间件
其他中间件
1、Maven下载地址
Maven下载地址:https://archive.apache.org/dist/maven/maven-3/
选择各大版本归档小版本
2、Git下载地址
Git下载地址:https://mirrors.edge.kernel.org/pub/software/scm/git/
2、JDK下载地址
JDK下载地址:https://www.oracle.com/java/technologies/downloads/archive/
右侧选择各大版本归档小版本,没有oracle账号注册一个,不要用网上乱传的jdk。
注册教程:https://blog.csdn.net/weixin_45686042/article/details/139008717
3、MySQL下载地址
MySQL下载地址:https://downloads.mysql.com/archives/community/
选择所需版本和适配系统
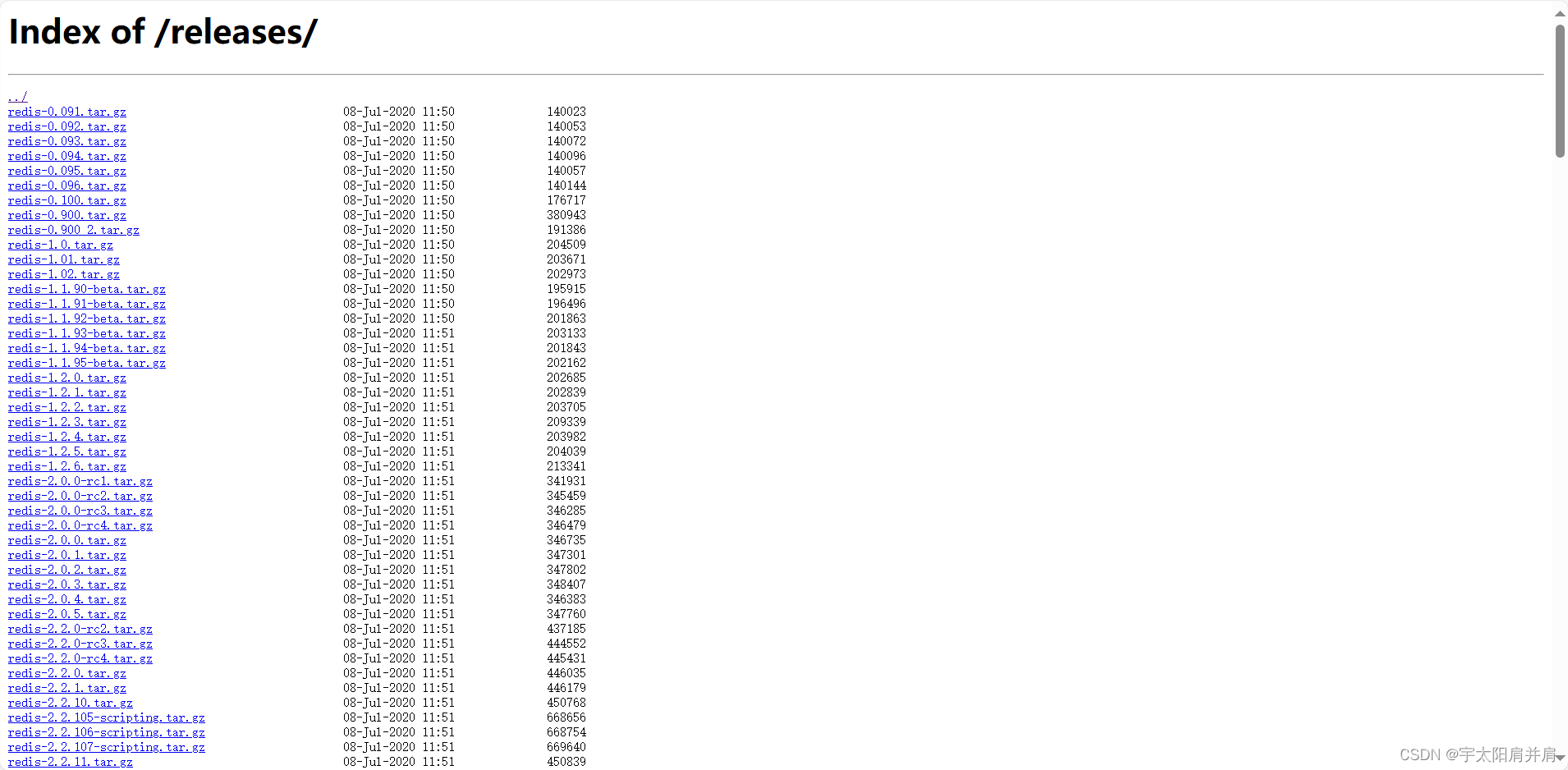
4、Redis下载地址
Redis下载地址:https://download.redis.io/releases/或https://github.com/tporadowski/redis/releases?page=1
5、Nacos下载地址
Nacos下载地址:https://nacos.io/download/release-history/

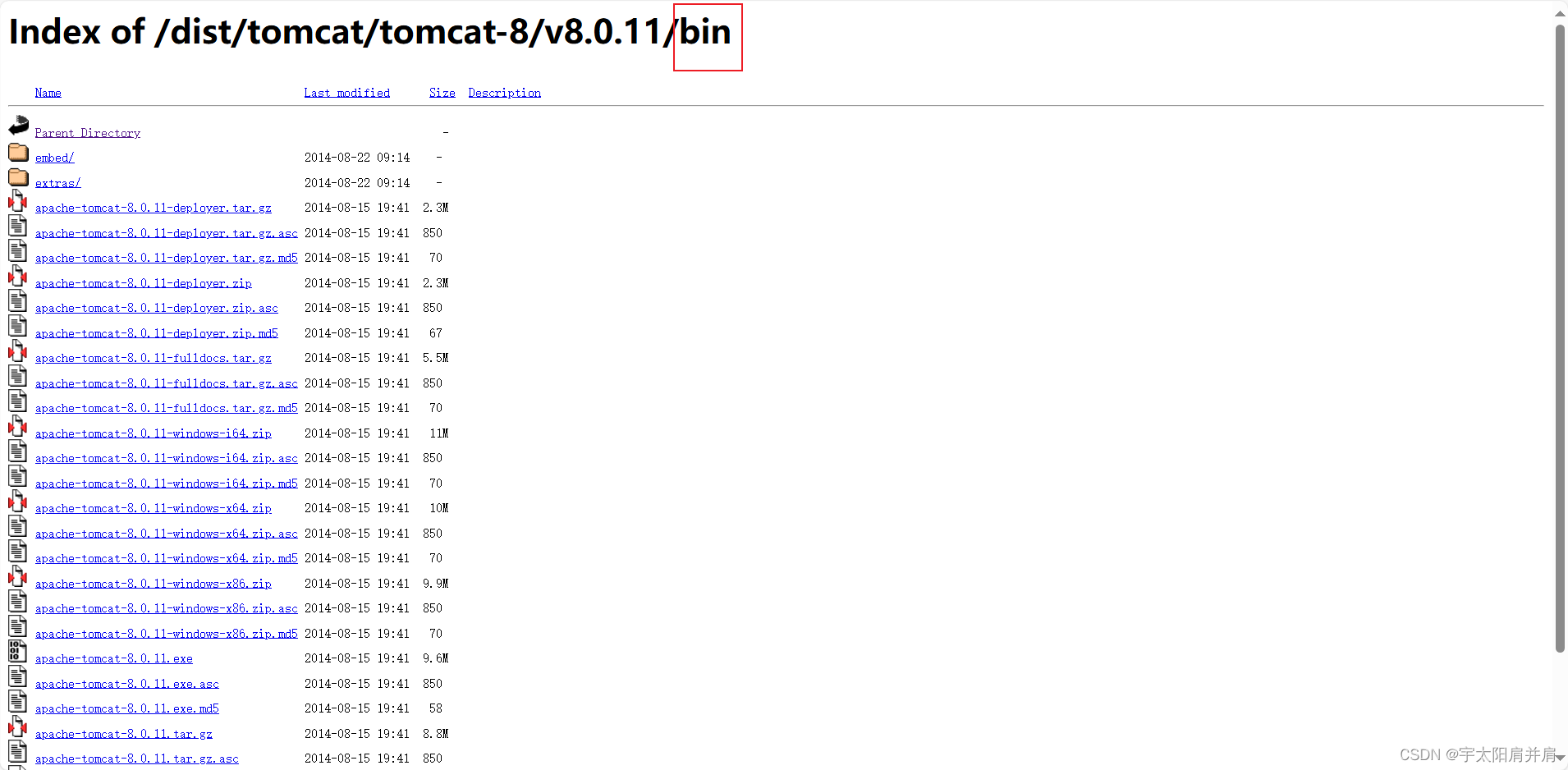
6、Tomcat下载地址
Tomcat下载地址:https://archive.apache.org/dist/tomcat/
找到小版本归档后进bin目录去寻所需压缩包
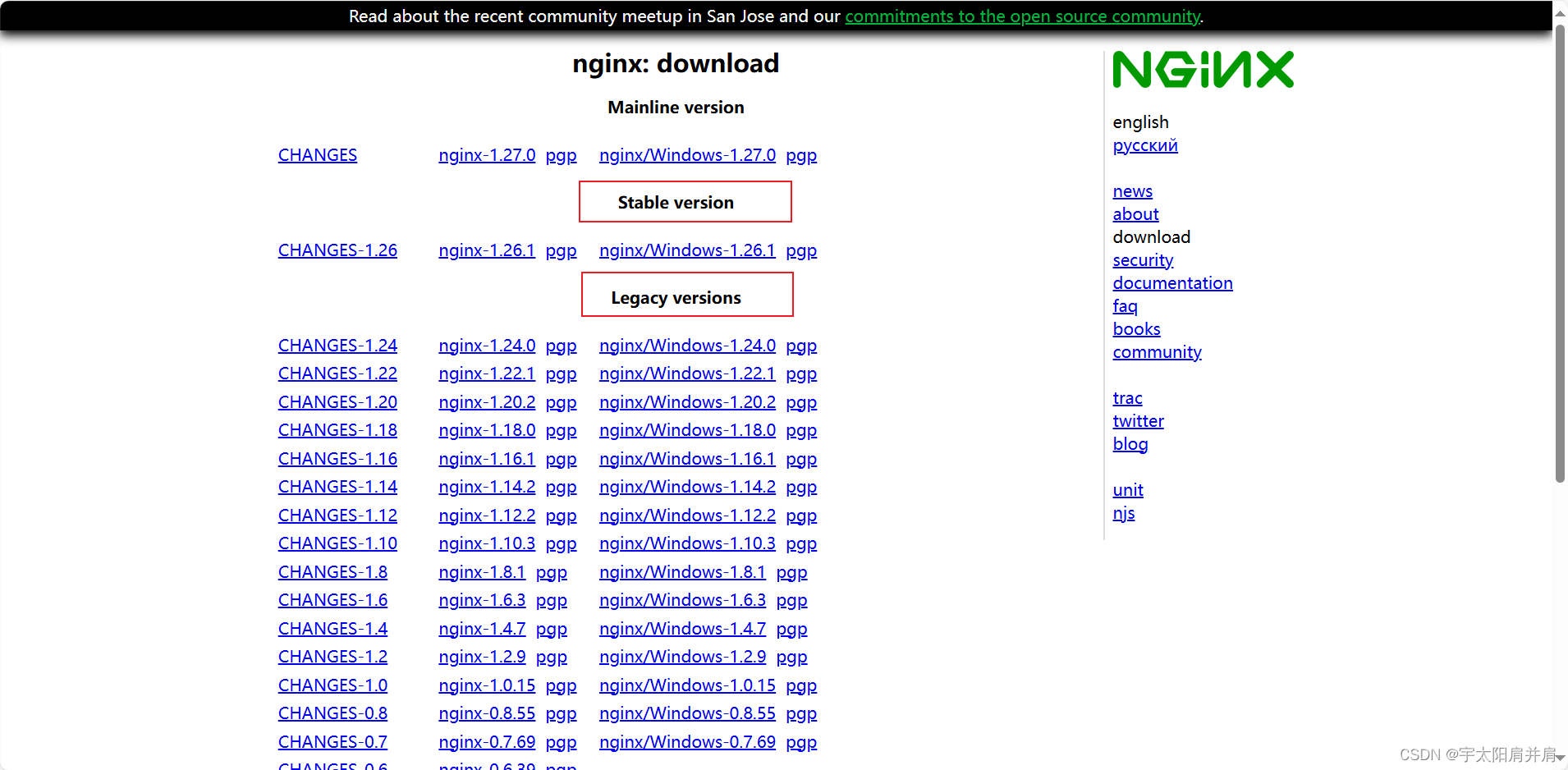
7、Nginx下载地址
Nginx下载地址:http://nginx.org/en/download.html
一般项目使用稳定版本Stable version,若有特殊需要选择下方历史版本Legacy versions,若没有测试需求,不要使用最新版本
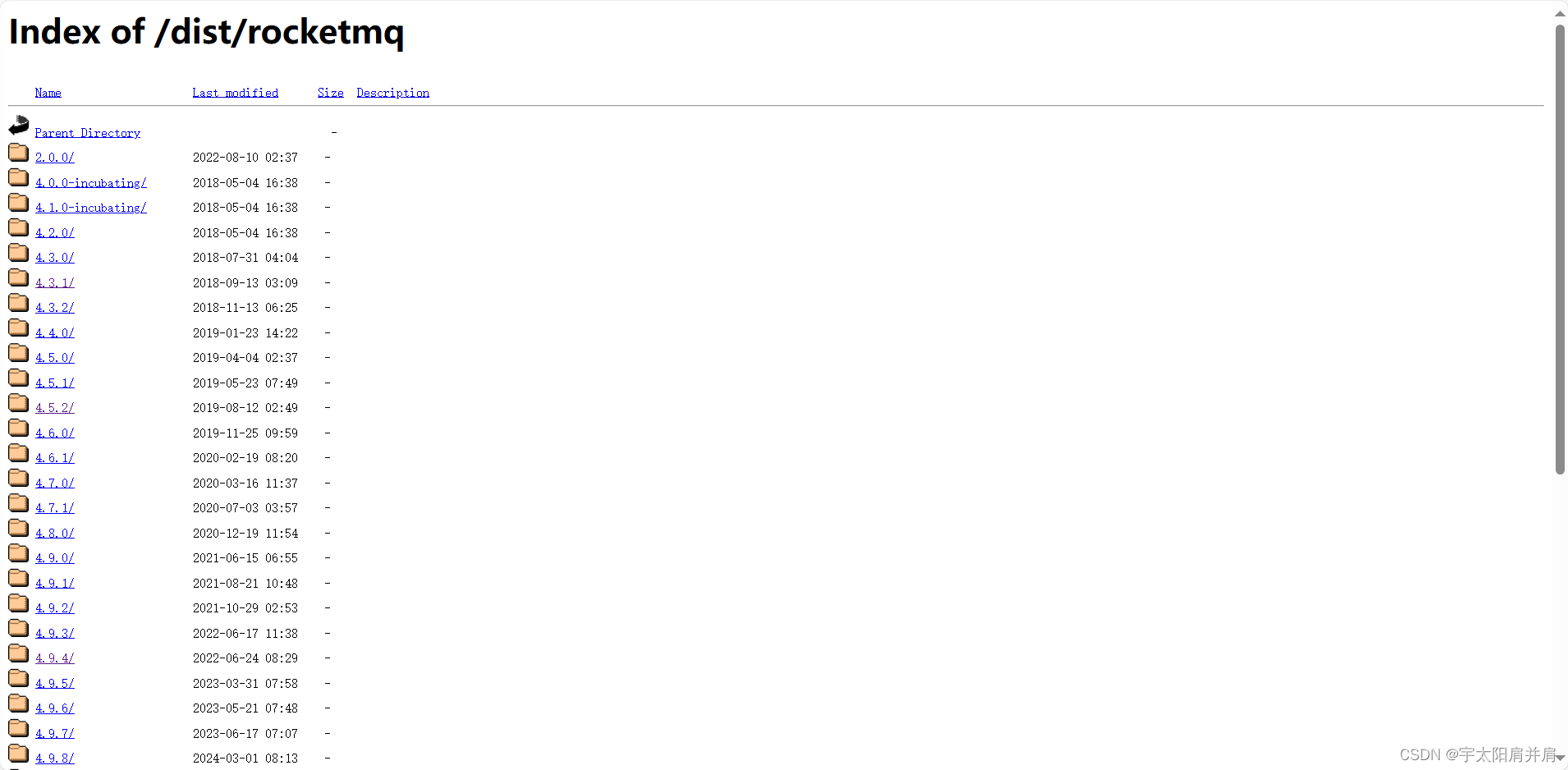
8、RocketMQ下载地址
RocketMQ下载地址:https://archive.apache.org/dist/rocketmq/
8、RabbitMQ下载地址
RabbitMQ下载地址:https://www.rabbitmq.com/release-information
或https://github.com/rabbitmq/rabbitmq-server/releases

8、Erlang下载地址
下载地址:https://github.com/rabbitmq/erlang-rpm/releases
需要注意RabbitMQ与Erlang是有兼容性的,兼容性对比链接:https://www.rabbitmq.com/docs/which-erlang
相关文章:

常用中间件各版本下载
常用中间件下载地址 前言分布式中间件负载均衡中间件缓存中间件数据库中间件其他中间件1、Maven下载地址2、Git下载地址2、JDK下载地址3、MySQL下载地址4、Redis下载地址5、Nacos下载地址6、Tomcat下载地址7、Nginx下载地址8、RocketMQ下载地址8、RabbitMQ下载地址8、Erlang下载…...

VsCode SSH远程设置不用重复输入密码
winR输入cmd,回车,输入 C:\Users\Administrator> ssh-keygen -t rsa -b 4096 Generating public/private rsa key pair. Enter file in which to save the key (C:\Users\Administrator/.ssh/id_rsa): Enter passphrase (empty for no passphrase): …...

【Linux】:进程切换
朋友们、伙计们,我们又见面了,本期来给大家解读一下有关Linux进程切换的知识点,如果看完之后对你有一定的启发,那么请留下你的三连,祝大家心想事成! C 语 言 专 栏:C语言:从入门到精…...

MongoDB CRUD操作:删除文档
MongoDB CRUD操作:删除文档 文章目录 MongoDB CRUD操作:删除文档删除集合的所有文档删除符合条件的所有文件删除第一个符合条件的文档## 在MongoDB Atlas中删除文档删除行为索引 原子性写确认 可以使用下面的方式删除MongoDB集合的文档: 使用…...

SpringBoot集成腾讯COS流程
1.pom.xml中添加cos配置 <!--腾讯cos --> <dependency><groupId>com.qcloud</groupId><artifactId>cos_api</artifactId><version>5.6.28</version> </dependency> 2.application.yaml中添加cos配置 # 腾讯云存储cos…...

中高级前端开发岗
定位: 日常迭代任务的核心研发,具备高质、高效完成迭代任务的能力。 素质要求: 业务专家或擅长某一方向技术;有较丰富的开发经验;需要具备良好的沟通和协作能力,能够与其他部门和团队进行有效的沟通和协…...
idea常用配置
文章目录 I 常见问题1.1 取消maven忽略文件清单1.2 源根之外的java文件1.3 idea取消所有断点1.4 idea使用非模式提交界面1.5 用Service窗口展示所有服务及端口1.6 idea编码问题(加载配置文件失败)II idea 换行后自动缩进4个空格,怎么取消?I 常见问题 1.1 取消maven忽略文件…...

Spring AOP 切面按照一定规则切片并行查询Mapper并返回
需求: 有时候我们在查询mapper层时,有时候可能由于入参数据过大或者查询的范围较大,导致查询性能较慢,此时 我们需要将原本的查询按照一定规则将查询范围进行切面,然后分片查询,最后将查询结果进行组装合并…...

【vue3|第4期】Vue3的选项式与组合式
日期:2024年5月30日 作者:Commas 签名:(ง •_•)ง 积跬步以致千里,积小流以成江海…… 注释:如果您觉得有所帮助,帮忙点个赞,也可以关注我,我们一起成长;如果有不对的地方…...

算法训练营第四十五天 | LeetCode 1049 最后一块石头的重量II、LeetCode 494 目标和、LeetCode 474 一和零
LeetCode 1049 最后一块石头的重量 继续昨天没有详细说的01背包问题往下继续说。01背包问题是将dp从一维问题升维到二维之后会遇到的一类典型问题。dp数组自然而然地是一个横坐标表示物品序号-1,纵坐标表示背包重量的二维数组。01背包由一个背包是否放该物品并比照后…...

【数据结构与算法(C 语言)】栈的基本操作函数(动图演示) 及 栈的实际应用之一:进制转换
目录 1. 前言2. 结构及基本操作函数:2.1 栈的结构类型 Stack2.2 初始化栈 InitStack2.3 销毁栈 DestroyStack2.4 清空栈 ClearStack2.5 判断栈是否为空 StackEmpty2.6 获取stack的长度 StackLength2.7 获取栈顶元素 GetTop2.8 入栈 Push2.9 出栈 Pop2.10 访问元素2.…...

[原创]C++ 11的thread_local线程局部变量与Lambda表达式配合使用, 却引发致命的, 难以发现的冲突.
[简介] 常用网名: 猪头三 出生日期: 1981.XX.XX QQ联系: 643439947 个人网站: 80x86汇编小站 https://www.x86asm.org 编程生涯: 2001年~至今[共22年] 职业生涯: 20年 开发语言: C/C、80x86ASM、PHP、Perl、Objective-C、Object Pascal、C#、Python 开发工具: Visual Studio、D…...
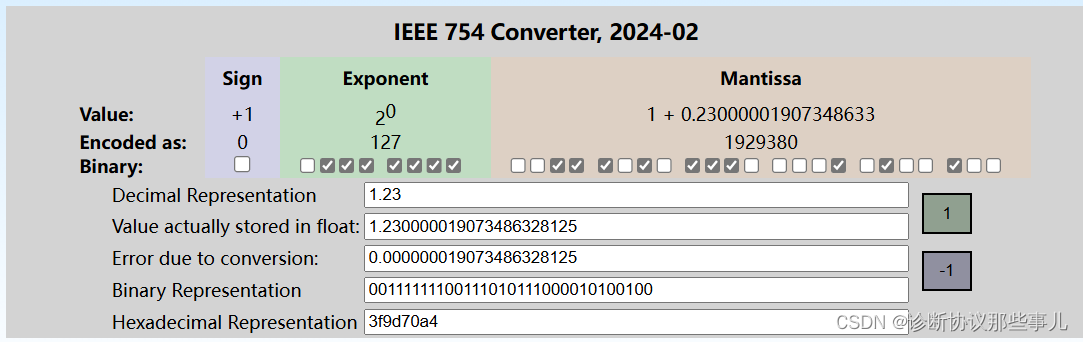
C语言-单精度和双精度浮点型
文章目录 一、遇到的问题二、解决方案三、问题根因float和double的区别: 总结-浮点数 一、遇到的问题 将NXP项目的代码移植到RH850F1K的项目上时,程序运行异常: u16Volt (uint16)((double)u16ADVal * (double)6.3) 执行到这一行程序就跑飞了…...

STM32学习问题总结(2)—CubeMX生成项目后串口没效果和Microlib
检查完所有的硬件和软件部分,最后发现,又是Keil的设置问题,啊啊啊啊 打开Keil的魔术棒,勾选Target的Use Microlib选项即可,但这并不是最佳方案 最终解决方案: 参考:http://t.csdnimg.cn/2Tjfc…...
【数据结构与算法 | 二叉树篇】二叉树的前中后序遍历(递归版本)
1. 二叉树的概念 (1). 二叉树的结构 借用了一下力扣的模板 public class TreeNode {int val;TreeNode left;TreeNode right;TreeNode() {}TreeNode(int val) { this.val val; }TreeNode(int val, TreeNode left, TreeNode right) {this.val val;this.left left;this.righ…...

Python exp用法:深入探索指数函数的奥秘
Python exp用法:深入探索指数函数的奥秘 在Python中,exp是一个非常重要的数学函数,它属于math模块的一部分,用于计算自然数e的指数。自然数e是一个无理数,约等于2.71828,它在数学、物理和工程等领域有着广…...
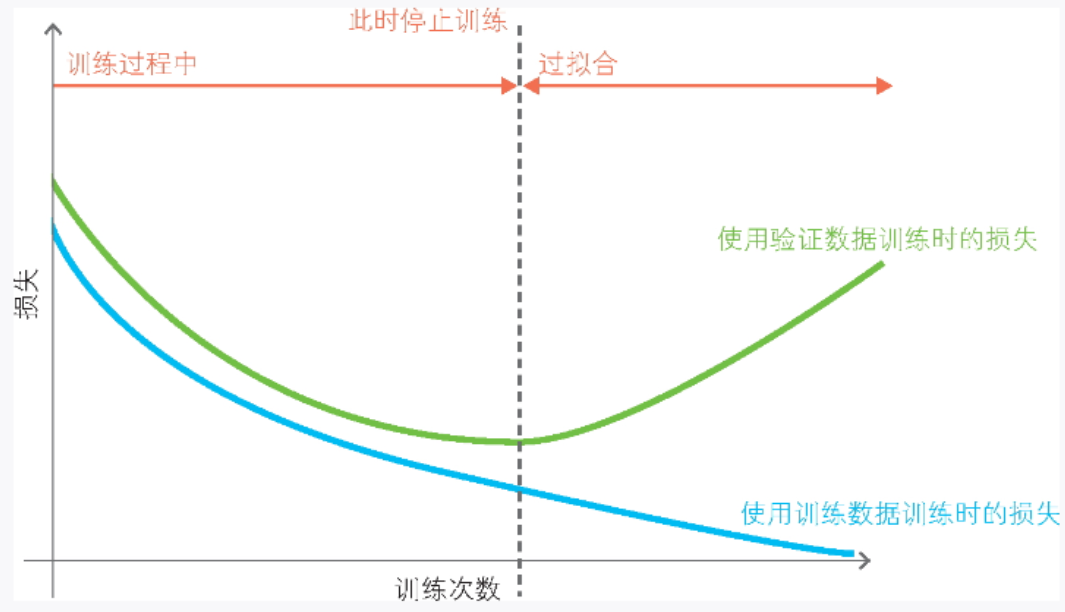
[有监督学习] 8.详细图解神经网络
神经网络 一直以来,人们都认为神经网络(Neural Network,NN)是模仿生物体的神经网络设计而成的。神经网络既可以用于回归,也可以用于分类,但在实际应用中常用于分类。基于神经网络的深 度学习因在图像识别和…...
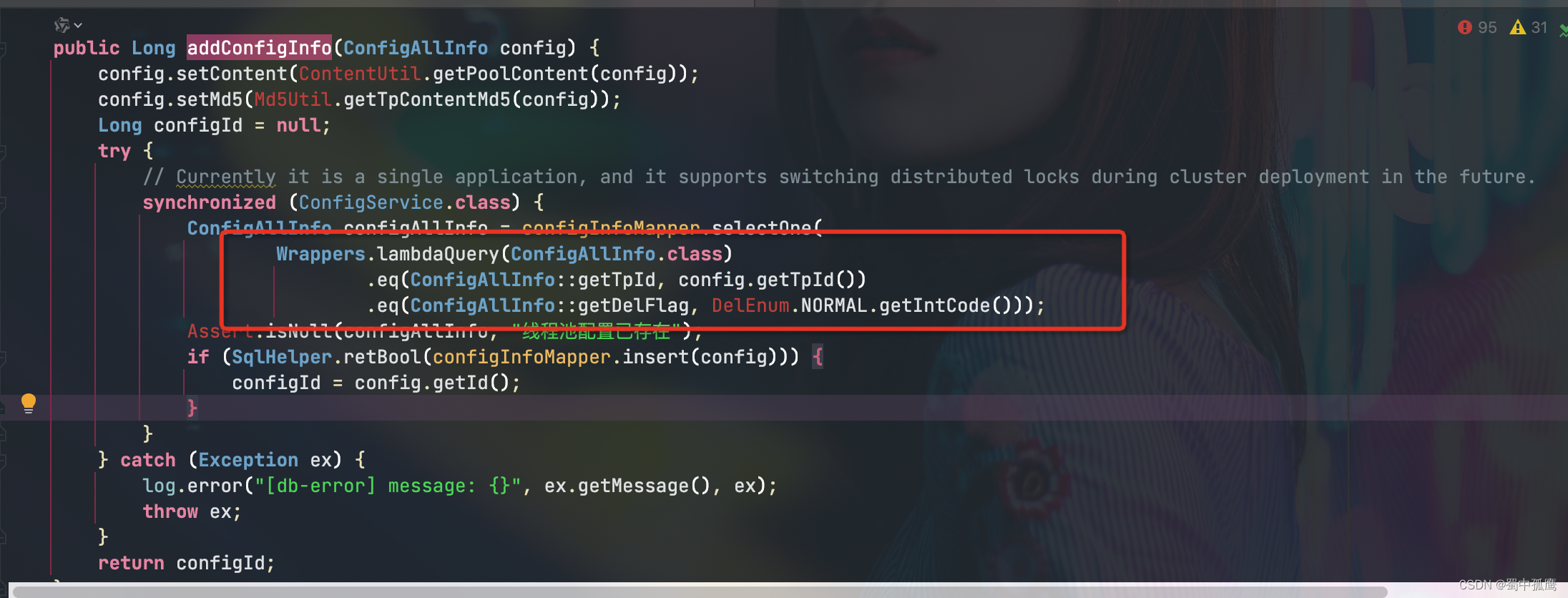
我给线程池管理框架hippo4j找bug
1 虚拟机参数不生效 hippo4j的docker启动脚本位于 docker/docker-startup.sh 。从下图可以看到 JAVA_OPT放在了jar包名 hippo4j-server.jar之后,而只有项目参数才放在jar包名之后。 实际上这里JAVA_OPT中包含虚拟机参数,而虚拟机参数要放在jar包名之前…...

win10键盘按乱了,如何恢复?
今天键盘被宝宝给按乱了,好不容易给重新调整回来,记录备忘: 1、win10的asdw和方向键互换了: 使用Fnw键来回切换,OK! 2、键盘的win键失效,例如:按winD无法显示桌面。此时…...

5.29工效学-人因工程人机交互
对于工效学这门课,一直都感觉很有意思,是一个值得再认真一点的课。可惜上课的时候效率不高,有感兴趣的东西课后也没有自行去拓展开来,前面的课我感觉还讲了比较重要的东西,但是,全忘了呢(真的对…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

centos 7 部署awstats 网站访问检测
一、基础环境准备(两种安装方式都要做) bash # 安装必要依赖 yum install -y httpd perl mod_perl perl-Time-HiRes perl-DateTime systemctl enable httpd # 设置 Apache 开机自启 systemctl start httpd # 启动 Apache二、安装 AWStats࿰…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

【开发技术】.Net使用FFmpeg视频特定帧上绘制内容
目录 一、目的 二、解决方案 2.1 什么是FFmpeg 2.2 FFmpeg主要功能 2.3 使用Xabe.FFmpeg调用FFmpeg功能 2.4 使用 FFmpeg 的 drawbox 滤镜来绘制 ROI 三、总结 一、目的 当前市场上有很多目标检测智能识别的相关算法,当前调用一个医疗行业的AI识别算法后返回…...

在 Spring Boot 中使用 JSP
jsp? 好多年没用了。重新整一下 还费了点时间,记录一下。 项目结构: pom: <?xml version"1.0" encoding"UTF-8"?> <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://ww…...

Kubernetes 节点自动伸缩(Cluster Autoscaler)原理与实践
在 Kubernetes 集群中,如何在保障应用高可用的同时有效地管理资源,一直是运维人员和开发者关注的重点。随着微服务架构的普及,集群内各个服务的负载波动日趋明显,传统的手动扩缩容方式已无法满足实时性和弹性需求。 Cluster Auto…...
)
41道Django高频题整理(附答案背诵版)
解释一下 Django 和 Tornado 的关系? Django和Tornado都是Python的web框架,但它们的设计哲学和应用场景有所不同。 Django是一个高级的Python Web框架,鼓励快速开发和干净、实用的设计。它遵循MVC设计,并强调代码复用。Django有…...

项目进度管理软件是什么?项目进度管理软件有哪些核心功能?
无论是建筑施工、软件开发,还是市场营销活动,项目往往涉及多个团队、大量资源和严格的时间表。如果没有一个系统化的工具来跟踪和管理这些元素,项目很容易陷入混乱,导致进度延误、成本超支,甚至失败。 项目进度管理软…...
