练习题-17
以下题目来自2024年5月清华大学“丘成桐数学科学领军计划数学水平考试”。第11题本人参考了网友Fiddie (数学兔的极大理想)的解答,原网址是 https://mp.weixin.qq.com/s/q9slRWL4iO_TcSdkmbfbbw.
第10题:在10维列向量构成的内积空间 V V V中,定义由向量 v v v引起的反射为 P v ( x ) = x − 2 ( x , v ) ( v , v ) v . P_v(x)=x-2\frac{(x,v)}{(v,v)}v. Pv(x)=x−2(v,v)(x,v)v. 今有向量 v , w ∈ V v, w\in V v,w∈V, 满足 0 < ( v , w ) < ( v , v ) ( w , w ) . 0< (v,w)<\sqrt{(v,v)\, (w,w)}. 0<(v,w)<(v,v)(w,w). 记 Q = P w ∘ P v Q=P_w \circ P_v Q=Pw∘Pv. 则所有满足 P ∘ Q = Q ∘ P P \circ Q = Q \circ P P∘Q=Q∘P的线性变换 P : V → V P: V \to V P:V→V构成的子空间的维数是多少?
解:依题意,向量 v , w v, w v,w线性无关. 不妨假设 v , w v, w v,w夹角为 θ / 2 ∈ ( 0 , π / 2 ) \theta/2 \in (0, \pi/2) θ/2∈(0,π/2) (注意 P v = P − v P_v = P_{-v} Pv=P−v. 必要时用 − v -v −v代替 v v v,即可保证夹角为锐角). 在二维子空间 W = s p a n ( v , w ) W=\mathrm{span}(v, w) W=span(v,w)中,线性变换 Q Q Q的效果是逆时针旋转 θ \theta θ. 熟知这可以用旋转矩阵 R θ = ( c − s s c ) R_\theta = \begin{pmatrix} c & -s \\ s & c \end{pmatrix} Rθ=(cs−sc)给出,其中 c = cos θ , s = sin θ c=\cos \theta,\; s= \sin \theta c=cosθ,s=sinθ. 而全部与 R θ R_\theta Rθ 乘法可交换的矩阵都是像 A a , b = ( a − b b a ) A_{a, b}=\begin{pmatrix} a & -b \\ b & a \end{pmatrix} Aa,b=(ab−ba)的形式。这些矩阵在全部2阶矩阵构成的线性空间中,组成了一个2维子空间。
在 V V V中, W W W的正交补 W ⊥ W^\perp W⊥是 8 8 8维的。在 W ⊥ W^\perp W⊥中进行任何的线性变换,都与 Q Q Q乘法可交换。所以所求的线性子空间维数是 8 × 8 + 2 = 66 8\times 8 + 2=66 8×8+2=66维。
注意:如果把10维改为一般的 n ( ≥ 2 ) n (\geq 2) n(≥2)维,那么答案是 ( n − 2 ) 2 + 2 (n-2)^2 + 2 (n−2)2+2维.
第11题: 10 10 10阶矩阵 A A A满足每行恰有 5 5 5个 1 1 1 和 5 5 5 个 0 0 0,且使得 A 2 + 5 A A^2+5A A2+5A是一个全部元素均为 5 5 5的矩阵. 问这样的矩阵 A A A有多少个?
解:(1) A A A的对角元不能是 1 1 1, 所以只能是 0 0 0. 这是因为如果 A A A有一个对角元是 1 1 1, A 2 + 5 A A^2+5A A2+5A相应的对角元就至少是 6 6 6.
(2) 用 J 2 n J_{2n} J2n表示元素全部是 1 1 1的 2 n 2n 2n阶方阵。从 A 2 + 5 A = 5 J 10 A^2+5A=5J_{10} A2+5A=5J10可知,如果 A A A的第 ( i , j ) (i,j) (i,j)位置是 1 1 1, 则 A 2 A^2 A2的第 ( i , j ) (i,j) (i,j)位置是 0 0 0; 如果 A A A的第 ( i , j ) (i, j) (i,j)位置是 0 0 0, 则 A 2 A^2 A2的第 ( i , j ) (i, j) (i,j)位置是 5 5 5. 由此可知, A A A的第 k k k列中 1 1 1的位置与 A A A的第 k k k行中 1 1 1的位置相同,所以 A A A是对称矩阵。
(3)从等式 A 2 + 5 A = 5 J 10 A^2+5A=5J_{10} A2+5A=5J10以及 A = A ⊤ A=A^\top A=A⊤可见,只要 A A A的第一行确定了,那么 A 2 A^2 A2的第一行, A A A的第一列也就确定了,从而 A A A的其它行也随之确定.
所以,只要 A A A的第一行确定了, A A A就被确定了。想要确定 A A A的第一行,只需要把 5 5 5个 1 1 1放到非对角线的位置(共 9 9 9个位置可选)。这等价于说把剩下的 4 4 4个 0 0 0放到第一行剩下的 9 9 9个位置。所以不同的 A A A共有 ( 9 5 ) = ( 9 4 ) = 126 \binom{9}{5}=\binom{9}{4}=126 (59)=(49)=126个.
注意:如果题目条件改为“ 2 n 2n 2n阶方阵 A A A满足 A 2 + n A = n J 2 n A^2+nA=nJ_{2n} A2+nA=nJ2n, 且 A A A的每行恰有 n n n个 0 0 0与 n n n个 1 1 1”. 则这样的方阵共有 ( 2 n − 1 n ) = ( 2 n − 1 n − 1 ) \binom{2n-1}{n}=\binom{2n-1}{n-1} (n2n−1)=(n−12n−1)个.
相关文章:

练习题-17
以下题目来自2024年5月清华大学“丘成桐数学科学领军计划数学水平考试”。第11题本人参考了网友Fiddie (数学兔的极大理想)的解答,原网址是 https://mp.weixin.qq.com/s/q9slRWL4iO_TcSdkmbfbbw. 第10题:在10维列向量构成的内积空间 V V V中…...

乐高小人分类项目
数据来源 LEGO Minifigures | Kaggle 建立文件目录 BASE_DIR lego/star-wars-images/ names [YODA, LUKE SKYWALKER, R2-D2, MACE WINDU, GENERAL GRIEVOUS ] tf.random.set_seed(1)# Read information about dataset if not os.path.isdir(BASE_DIR train/):for name in …...

个人关于ChatGPT的用法及建议
概述 这里只是个人常用的几个软件,做一下汇总,希望对各位有用。 如果有更高认知的朋友,请留下你的工具名称,提醒我一下,谢谢~ 常用的chatgpt模型工具: 以下是一些知名的例子: 文…...

神经网络的工程基础(二)——随机梯度下降法|文末送书
相关说明 这篇文章的大部分内容参考自我的新书《解构大语言模型:从线性回归到通用人工智能》,欢迎有兴趣的读者多多支持。 本文涉及到的代码链接如下:regression2chatgpt/ch06_optimizer/stochastic_gradient_descent.ipynb 本文将讨论利用…...

常见的几种编码方式
常见的编码方式及其特点: 编码方式的设计是为了适应不同的字符集和应用需求,因此它们在表示字符时使用的位数和字节数各不相同 常见编码方式及其位数和字节数 ASCII(American Standard Code for Information Interchange)&#x…...
ubuntu移动硬盘重命名
因为在ubuntu上移动硬盘的名字是中文的,所以想要改成英文的。 我的方法: 将移动硬盘插到windows上,直接右键重命名。再插到ubuntu上名字就改变了。 别人的方法: ubuntu下如何修改U盘名字-腾讯云开发者社区-腾讯云 在自带的软件…...

VUE框架前置知识总结
一、前言 在学习vue框架中,总是有些知识不是很熟悉,又不想系统的学习JS,因为学习成本太大了,所以用到什么知识就学习什么知识。此文档就用于记录零散的知识点。主要是还是针对与ES6规范的JS知识点。 以下实验环境都是在windows环…...

张宇1000题80%不会?别急,这个方法肯定有用!
这太正常了,1000题的难度本来就高,不要慌 我考研的时候跟的也是张宇老师,但是1000题我根本就没做几道题就给换成880题660题了,而且只是强化阶段用880题,基础阶段我用的都是汤家凤的1800题。 不要担心做的不是张宇老师…...

【python】爬虫记录每小时金价
数据来源: https://www.cngold.org/img_date/ 因为这个网站是数据随时变动的,用requests、BeautifulSoup的方式解析html的话,数据的位置显示的是“--”,并不能取到数据。 所以采用webdriver访问网站,然后从界面上获取…...
一行命令将已克隆的本地Git仓库推送到内网服务器
一、需求背景 我们公司用gitea搭建了一个git服务器,其中支持win7的最高版本是v1.20.6。 我们公司的电脑在任何时候都不能连接外网,但是希望将一些开源的仓库移植到内网的服务器来。一是有相关代码使用的需求,二是可以建设一个内网能够查阅的…...

Linux文本处理三剑客(详解)
一、文本三剑客是什么? 1. 对于接触过Linux操作系统的人来说,应该都听过说Linux中的文本三剑客吧,即awk、grep、sed,也是必须要掌握的Linux命令之一,三者都是用来处理文本的,但侧重点各不相同,a…...
AI在线UI代码生成,不需要敲一行代码,聊聊天,上传图片,就能生成前端页面的开发神器
ioDraw的在线UI代码生成器是一款开发神器,它可以让您在无需编写一行代码的情况下创建前端页面。 主要优势: 1、极简操作:只需聊天或上传图片,即可生成响应式的Tailwind CSS代码。 2、节省时间:自动生成代码可以节省大…...

go-zero整合单机版ClickHouse并实现增删改查
go-zero整合单机版ClickHouse并实现增删改查 本教程基于go-zero微服务入门教程,项目工程结构同上一个教程。 本教程主要实现go-zero框架整合单机版ClickHouse,并暴露接口实现对ClickHouse数据的增删改查。 go-zero微服务入门教程:https://b…...
行政工作如何提高效率?桌面备忘录便签软件哪个好
在行政管理工作中,效率的提高无疑是每个行政人员都追求的目标。而随着科技的发展,各种便捷的工具也应运而生,其中桌面备忘录便签软件便是其中的佼佼者。那么,这类软件又如何帮助我们提高工作效率呢? 首先,…...

利用向日葵和微信/腾讯会议实现LabVIEW远程开发
利用向日葵远程控制软件结合微信或腾讯会议的视频通话功能,可以实现LabVIEW的远程开发和调试。通过向日葵进行远程桌面访问,配合视频通话工具进行实时沟通与问题解决,不仅提高了开发效率,还减少了地域限制带来的不便。介绍这种远程…...
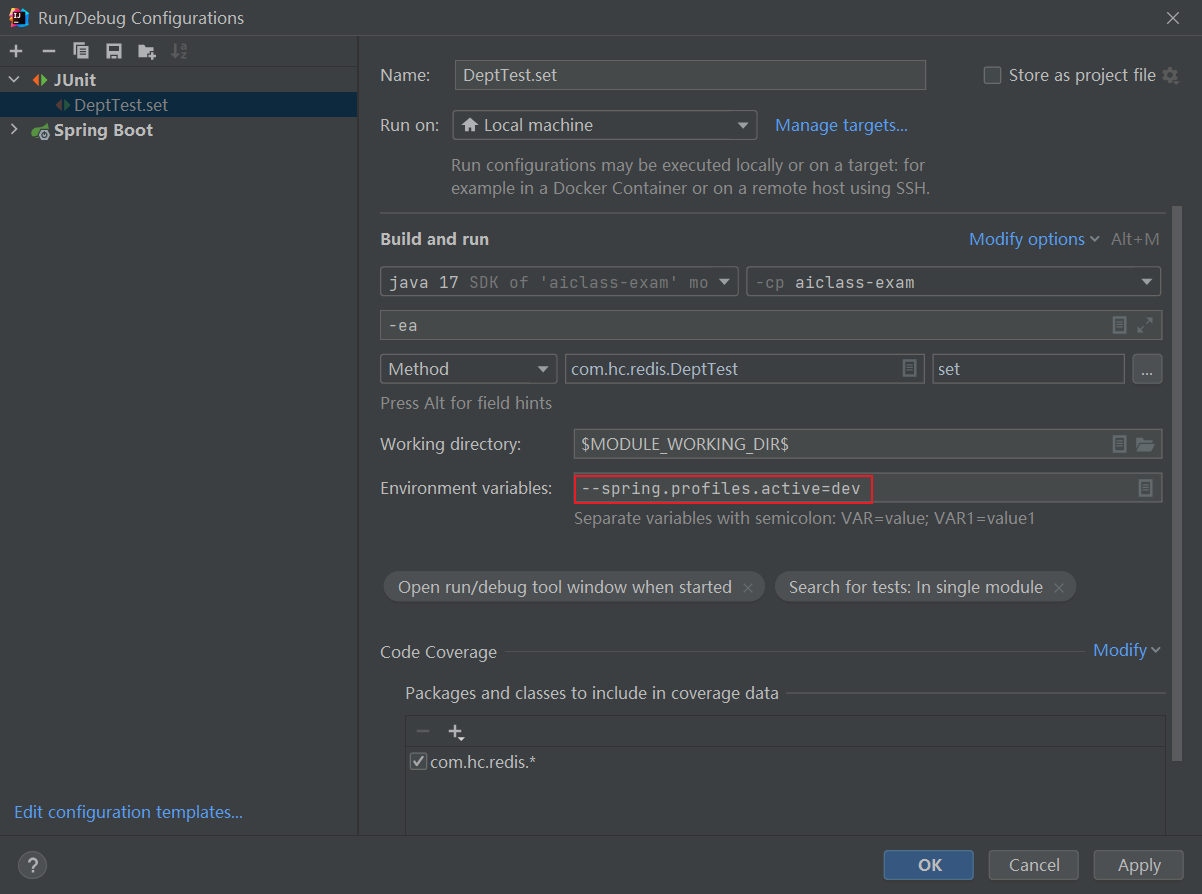
SpringBoot 单元测试 指定 环境
如上图所示,在配置窗口中添加--spring.profiles.activedev,就可以了。...

Flutter 中的 SliverOpacity 小部件:全面指南
Flutter 中的 SliverOpacity 小部件:全面指南 Flutter 是一个功能强大的 UI 框架,由 Google 开发,允许开发者使用 Dart 语言来构建高性能、美观的跨平台应用。在 Flutter 的滚动组件体系中,SliverOpacity 是一个用来为其子 Slive…...

源码分析の前言
源码分析路线图: 初级部分:ArrayList->LinkedList->Vector->HashMap(红黑树数据结构,如何翻转,变色,手写红黑树)->ConcurrentHashMap 中级部分:Spring->Spring MVC->Spring Boot->M…...
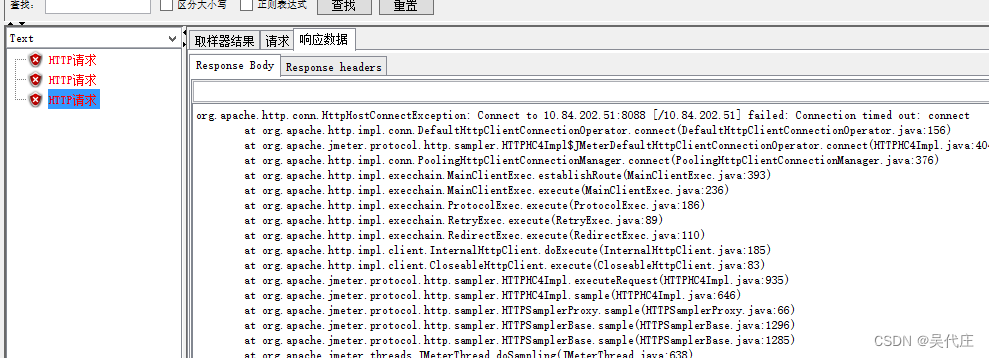
接口性能测试复盘:解决JMeter超时问题的实践
在优化接口并重新投入市场后,我们面临着一项关键任务:确保其在高压环境下稳定运行。于是,我们启动了一轮针对该接口的性能压力测试,利用JMeter工具模拟高负载场景。然而,在测试进行约一分钟之后,频繁出现了…...

[数据集][目标检测]猕猴桃检测数据集VOC+YOLO格式1838张1类别
数据集格式:Pascal VOC格式YOLO格式(不包含分割路径的txt文件,仅仅包含jpg图片以及对应的VOC格式xml文件和yolo格式txt文件) 图片数量(jpg文件个数):1838 标注数量(xml文件个数):1838 标注数量(txt文件个数):1838 标注…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

用docker来安装部署freeswitch记录
今天刚才测试一个callcenter的项目,所以尝试安装freeswitch 1、使用轩辕镜像 - 中国开发者首选的专业 Docker 镜像加速服务平台 编辑下面/etc/docker/daemon.json文件为 {"registry-mirrors": ["https://docker.xuanyuan.me"] }同时可以进入轩…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

【JVM面试篇】高频八股汇总——类加载和类加载器
目录 1. 讲一下类加载过程? 2. Java创建对象的过程? 3. 对象的生命周期? 4. 类加载器有哪些? 5. 双亲委派模型的作用(好处)? 6. 讲一下类的加载和双亲委派原则? 7. 双亲委派模…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
:LeetCode 142. 环形链表 II(Linked List Cycle II)详解)
Java详解LeetCode 热题 100(26):LeetCode 142. 环形链表 II(Linked List Cycle II)详解
文章目录 1. 题目描述1.1 链表节点定义 2. 理解题目2.1 问题可视化2.2 核心挑战 3. 解法一:HashSet 标记访问法3.1 算法思路3.2 Java代码实现3.3 详细执行过程演示3.4 执行结果示例3.5 复杂度分析3.6 优缺点分析 4. 解法二:Floyd 快慢指针法(…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

Qt的学习(一)
1.什么是Qt Qt特指用来进行桌面应用开发(电脑上写的程序)涉及到的一套技术Qt无法开发网页前端,也不能开发移动应用。 客户端开发的重要任务:编写和用户交互的界面。一般来说和用户交互的界面,有两种典型风格&…...
