2024蓝桥杯国赛C++研究生组游记+个人题解
Day0
开始复习,过了一遍大部分板子
本来打算再学一遍SAM,但是想到去年考了字符串大题今年应该不会再考了吧。。
过了一遍数据结构和图论,就1点了
两点的时候还没睡着,舍友打游戏好像打到2点过。。
Day1
相当困
第一题:
数田字有多少条直线可以只经过两个点,12条
第二题:
求长度42的置换中,周期恰好为2024的置换个数
首先2024=8*11*23,然后8+11+23=42,然后就是组合数C(42,8)*C(34,11)
结果赛后复盘的时候发现不对劲,想简单了,还有环内部的顺序需要计算,应该还要乘上每个环长度的欧拉函数值(?
第三题:
限流器,T条访问记录,每条访问记录有一个时间戳,每n个时间单位作为一个限流区间,每个区间最多能提供m次访问机会。求成功访问的次数。
由于时间给的很小(<=1000),直接除一下n,放桶里,最后和m取min再求和。
第四题:
给一个数组a[i],求把所有数加上x再mod k之后,小于等于t的数最多能有多少个
先对所有a[i] mod一下k,变成求一段长度为t+1的区间最多能够覆盖多少值,由于这个问题是环形的,我们套路地把数组a[i]的每个值加上k的复制一段在后面,转化为区间问题。
贪心一下,我们选取的区间左端点一定是某个a[i]值,否则就可以让区间更靠后,以此获取更多覆盖的区域。
two-pointers扫一遍就可以知道结果了。注意边界条件判断。
当然,数据范围比较温和,二分查找logn也可以过。
此时9:34。
第五题:
小模拟,模拟vim指令编辑字符串,n^3
发现insert是中文引号,很诡异,但是不影响结果
这题写了我一个小时,厉害吧,我是真的唐啊
写完10:24了
第六题:
一个字符串,定义一个合法划分:划分中任意两个相邻的子串不能有公共字符。求该字符串中所有长度为1~5的本质不同的子串,这些子串在任意一个合法划分中都没有出现,请将他们按字典序输出。
首先,合法划分必然存在(怎么有点像绕口令),ababaabb可分为a|b|a|b|aa|bb
考虑一个串能在合法划分中出现,例如abcde,那么他的两端必然没有与a、b、c、d、e这五个字符相同的字符,否则这个子串就不能被划分出来。
于是我们枚举所有长度1~5的串,判断他是否能在合法划分中出现,能的话就给他的哈希值打上一个标记,因为字符串长度只有5,map+long long就可以过。
然后我们第二次,扫描所有长度为1~5的子串,看哈希值是否被标记过,如果没有就加入答案的集合。
最后对答案集合进行排序、去重就结束了。
ps:为什么不直接求不合法的子串,因为一段字符串中,aabaccaba,例如aba实际上是可以在合法划分中出现的,划分为:aa|b|a|cc|aba,但是如果直接求的话,a|aba|cc|a|b|a就发现前面这里的aba实际上不合法。
写完调完直接11:00
第七题:
一个带权有向图n个点(n<=50),给出邻接矩阵,m次查询(m<=1000),查询u点到v点恰好经过c条边的最短路径,并且可以将路径上的一条边边权减半(但是多次经过的话只能减半一次)。
一眼就是倍增floyd,再加上一个求路径max,同样可以倍增做。
不过时间复杂度非常逆天O(m*n^3*logc),考虑怎么优化
发现我不会,70分遗憾离场。
此时11:32,很急,后面还有三道大题没看。
第八题:
给一段序列,它来源于对一棵树的先序遍历的节点深度,已知该序列的一部分(未知的部分用-1
代替),求这个序列一共有多少种可能。
首先发现,先序遍历的深度序列任意一个值都满足a[i]<=a[i-1]+1(i>1)
然后,对于每一段-1,我们都可以对其进行计数。
设f[i][j]为第i位的值为j时,序列1~i构成的方案数
f[i][j]=f[i-1][j-1]+f[i-1][j]+f[i-1][j+1]+……+f[i-1][i-1],即对前一个f[i-1]的一个后缀和,再向后平移一位
假设这一段-1(区间为[l,r])的前一个数为x,后一个数为y,那么设f[l-1][x]=1
最终答案为f[r+1][y]
最后把每段的答案乘起来就是最终答案。
考虑如何优化这个后缀和
发现我不会,30分遗憾离场。
做完之后12:15,顿时觉得可以开摆了。
赛后复盘其实觉得不应该放弃这一点的,毕竟初值只有一个1,后面也只查询一个点,应该是可以用数学公式推出来的。
第九题:
n个点,每两个点i,j之间有一条边,若i*j为完全平方数则边权为1,否则为0。
特殊生成树定义为任意一个点都必定有一条边连接一个比自己权值小的点。
对每个k,求边权为k(k=0~n-1)的特殊生成树有多少个。
首先,这个特殊的性质规定了生成树的产生方式:顺序枚举1~n点,依次加入生成树,并且只能选择1~i-1的其中一个点进行连接。
于是乎,我们维护的n-1个点的答案数组f[i],表示边权为i的生成树有多少个,
在加入点n之后f[i]=cnt*f[i-1]+(n-1-cnt)*f[i],cnt表示n与1~n-1中乘积为完全平方数的个数。
这样就可以n^2拿到60分
至于85分就是分治NTT,模数还正好是998244353,相当于求一下乘积Π(i-1-cnti+cnti*x)的多项式系数。
最后的100分应该是NTT过程中其实可以优化,因为cnti可能为0,这样可以在常数上小一点,然后n(logn)^2过掉。
只可惜时间不够,但即便是时间够,我也不会写NTT了。。。。
真的很菜欸。。60分遗憾离场了。
至于cnt的求法,先把n分解质因数,对每个质因子次数ai,如果是偶数就凑(0、2、4、……、ai)
如果是奇数就凑(1、3、5、……、ai),也就是(ai+1)/2种凑法。然后把每个质因子凑法乘起来再-1(减掉本身)就是cnt了。复杂度O(n*sqrt(n))
如果不去掉本身的话,似乎还是个积性函数,应该可以线性筛筛出来?(这个纯口胡,有错的话还请大佬指正)
第十题:
真的不会一点啊
一排格子1~T,每个格子上最多有一个小球,可以没有,每个小球有一个数值ai,每个时刻,每个小球都有1/2的概率向右走一步,若一个小球走到T处则记录它的数值,并且把它拿走。
当有一个小球追上另一个小球时,两个小球会合并成一个新的小球,新的小球的数值为原来两个小球的乘积。
求在T处所记录的小球数值的和的期望。
T<=100, ai<=100
没时间做,也不会做。(23333
隐隐约约感觉是一个O(n^3)期望DP,不过我是真的不会。
相关文章:

2024蓝桥杯国赛C++研究生组游记+个人题解
Day0 开始复习,过了一遍大部分板子 本来打算再学一遍SAM,但是想到去年考了字符串大题今年应该不会再考了吧。。 过了一遍数据结构和图论,就1点了 两点的时候还没睡着,舍友打游戏好像打到2点过。。 Day1 相当困 第一题&…...
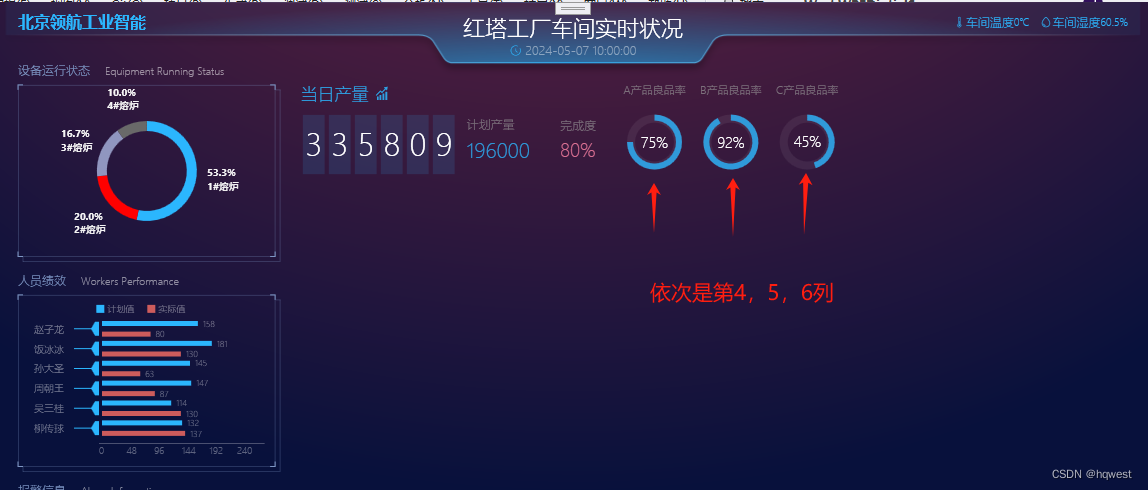
C#WPF数字大屏项目实战07--当日产量
1、第2列布局 第2列分三行,第一行分6列 2、当日产量布局 3、产量数据布局 运行效果 4、计划产量和完成度 运行效果 5、良品率布局 1、添加用户控件 2、用户控件绘制圆 2、使用用户控件 3、运行效果 4、注意点 这三个数值目前是静态的,可以由后台程序项…...
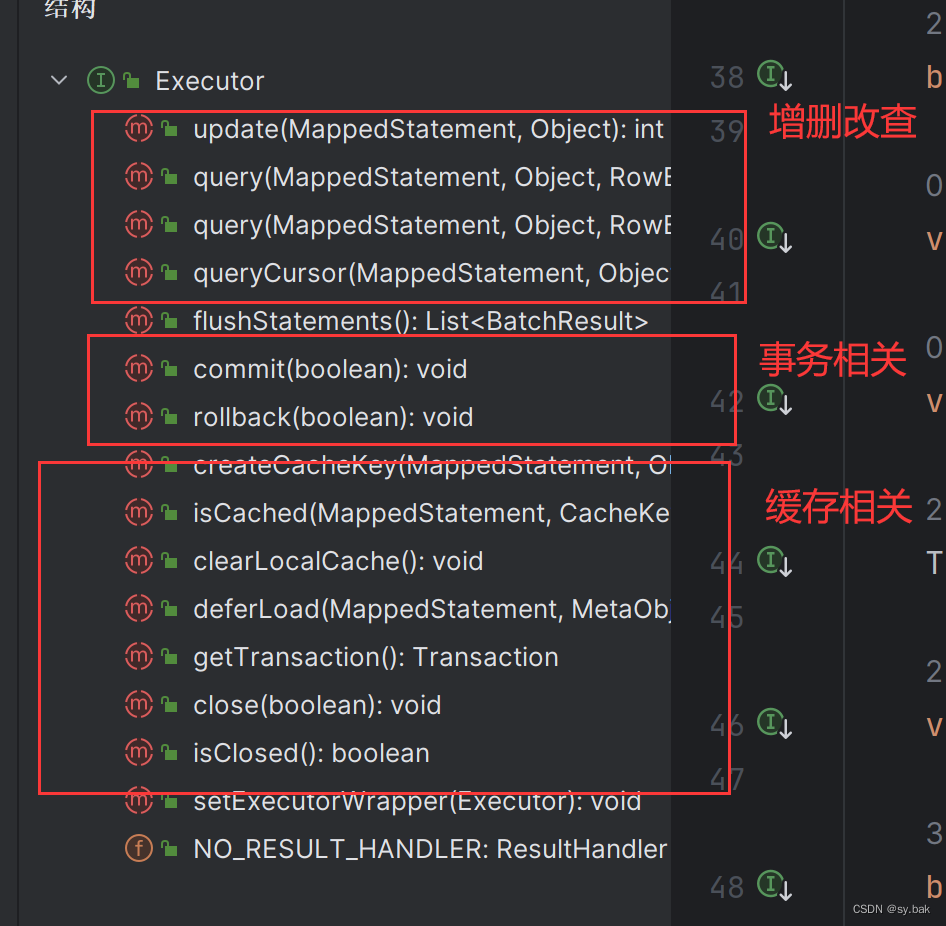
MyBatis源码分析--02:SqlSession建立过程
我们再来看看MyBatis使用流程: InputStream inputStream Resources.getResourceAsStream("myBatis_config.xml"); SqlSessionFactory sqlSessionFactory new SqlSessionFactoryBuilder().build(inputStream); SqlSession session sqlSessionFactory.op…...
SOUI Combobox 实现半透明弹出下拉框
SOUI默认情况下combobox的弹出框不是半透明的,这个时候如果背景透明时,滚动条会出现黑色背景,这个时候只需要在在combobox下添加一个子节点 <dropdownStyle translucent"1"></dropdownStyle> 这样一个窗口默认即实现…...
【含Python源码 MX_002期】)
Python 猜数系统 PyQt框架 有GUI界面 (源码在最后)【含Python源码 MX_002期】
一、系统简介 猜数界面是一个基于PyQt框架创建的简单图形用户界面(GUI),用于让用户参与猜数字游戏。简要介绍一下界面的各个部分: 游戏开始按钮:点击此按钮开始游戏。在点击前,需要在文本框中输入参与游戏…...
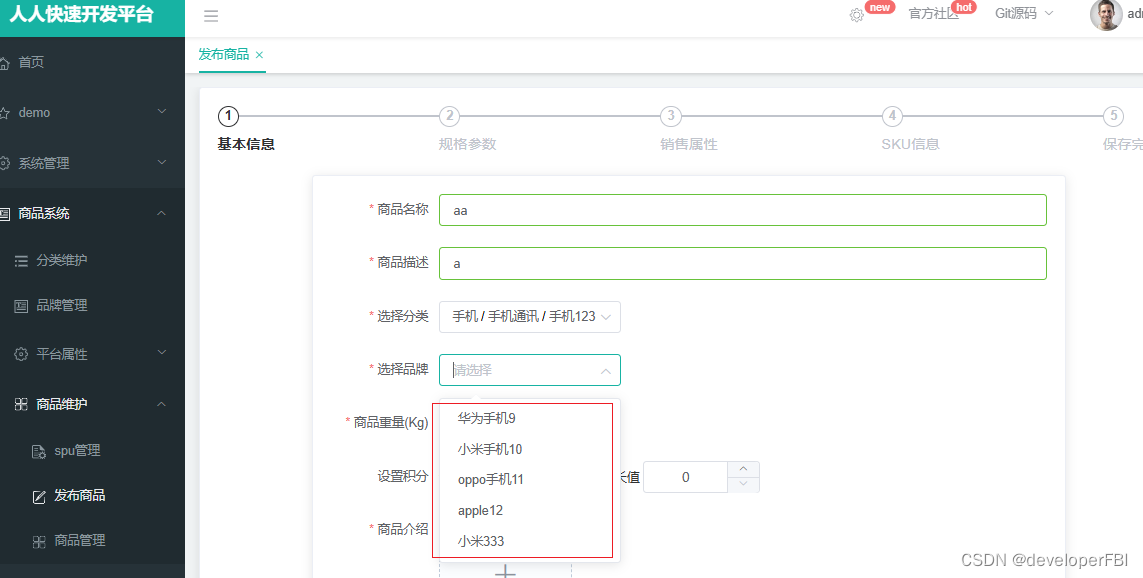
npm install pubsub-js报错的解决汇总
我在练习谷粒商城P83时,选择分类时触发向后端请求选择分类catId绑定的品牌数据,发现前端控制台报错: "PubSub is not definded",找不到pubsub。 因为缺少pubsub包,所以开始安装此包。 于是在网上一顿搜索猛如虎&…...
nuxt2:自定义指令 / v-xxx / directives / 理解 / 使用方法 / DEMO
一、理解自定义指令 在 vue 中提供了一些对于页面和数据更为方便的输出,这些操作就叫做指令,以 v-xxx 表示,比如 html 页面中的属性 <div v-xxx ></div>。自定义指令很大程度提高了开发效率,提高了工程化水平&#x…...

基础—SQL—DCL(数据控制语言)小结
一、总结 在SQL分类中的DCL语句部分,主要讲到了两个部分的知识。 1、用户管理 用户管理,主要是管理哪些用户可以访问当前 mysql 数据库。 包括:创建用户、修改用户密码以及删除用户 2、权限控制 权限管理,主要是控制我们当前用户…...

一文彻底讲透 PyTorch
节前,我们组织了一场算法岗技术&面试讨论会,邀请了一些互联网大厂朋友、今年参加社招和校招面试的同学。 针对大模型技术趋势、大模型落地项目经验分享、新手如何入门算法岗、该如何准备面试攻略、面试常考点等热门话题进行了深入的讨论。 汇总合集…...

JVM常用概念之锁粗化和循环
1.什么是锁粗化 锁粗化一般指有效地合并几个相邻的锁定块,从而减少锁定开销。如下述代码所示: 锁粗化前代码: synchronized (obj) {// statements 1 } synchronized (obj) {// statements 2 }锁粗化后代码: synchronized (obj)…...
)
HTML (总结黑马的)
<br>换行 <hr>水平线 div 独占一行 span 不换行 header 网页头部 nav 网页导航 footer 网页底部 aside 网页侧边栏 section 网页区块 article 网页文章 空格 < 小于号 > 大于号 图片: <img src"./cat.jpg" alt&q…...

YOLOv8 segment介绍
1.YOLOv8图像分割支持的数据格式: (1).用于训练YOLOv8分割模型的数据集标签格式如下: 1).每幅图像对应一个文本文件:数据集中的每幅图像都有一个与图像文件同名的对应文本文件,扩展名为".txt"; 2).文本文件中每个目标(object)占一行…...

PMBOK® 第六版 项目整合管理概念
目录 读后感—PMBOK第六版 目录 项目往往会牵涉到众多专业的知识以及来自不同专业、具有不同性格且可能处在不同地理位置的人员,存在着诸多不同分工的状况。要是没有统一的目标,相互之间也没有有效的沟通机制,并且不存在计划、监控以及平衡等…...

【Qt】【模型视图架构】代理模型
文章目录 代理模型简单介绍QSortFilterProxyModel类简单介绍排序过滤子类化 代理模型简单介绍 代理模型的作用是可以将一个模型中的数据进行排序或者过滤,然后提供给视图进行显示。 如下所示,创建一个源模型、一个代理模型,界面上创建一个列…...
Flutter 中的 IconTheme 小部件:全面指南
Flutter 中的 IconTheme 小部件:全面指南 Flutter 是一个功能丰富的 UI 开发框架,它允许开发者使用 Dart 语言来构建跨平台的移动、Web 和桌面应用。在 Flutter 的丰富组件库中,IconTheme 是一个用于设置应用中图标主题的小部件,…...

virtualbox虚拟机、centos7安装增强工具
文章目录 1. virtualBox语言设置2. 设置终端启动快捷键3. 添加virtualbox 增强工具4. 设置共享文件夹 1. virtualBox语言设置 virtualbox -> file -> perferences -> language ->选择对应的语言 -> OK virtualbox -> 管理 -> 全局设定 -> 语言 -> …...

Kotlin 泛型
文章目录 定义泛型属性泛型函数泛型类或接口 where 声明多个约束泛型具体化in、out 限制泛型输入输出 定义 有时候我们会有这样的需求:一个类可以操作某一类型的对象,并且限定只有该类型的参数才能执行相关的操作。 如果我们直接指定该类型Intÿ…...
)
Tomcat 面试题(一)
1. 简述什么是Tomcat ? Tomcat是一个开源的Java Servlet容器,它实现了Java Servlet和JavaServer Pages (JSP)技术,提供了一个运行Java Web应用程序的平台。Tomcat由Apache软件基金会维护,并广泛用于开发和部署Web应用程序。 Tom…...

跟踪一个Pytorch Module在训练过程中的内存分配情况
跟踪一个Pytorch Module在训练过程中的内存分配情况 代码输出 目的:跟踪一个Pytorch Module在训练过程中的内存分配情况 方法: 1.通过pre_hook module的来区分module的边界 2.通过__torch_dispatch__拦截所有的aten算子,计算在该算子中新创建tensor的总内存占用量 3.通过tensor…...
空间方法×3))
LeetCode 2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法×3)
【LetMeFly】2965.找出缺失和重复的数字:小数据?我选择暴力(附优化方法清单:O(1)空间方法3) 力扣题目链接:https://leetcode.cn/problems/find-missing-and-repeated-values/ 给你一个下标从 0 开始的二维…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

在软件开发中正确使用MySQL日期时间类型的深度解析
在日常软件开发场景中,时间信息的存储是底层且核心的需求。从金融交易的精确记账时间、用户操作的行为日志,到供应链系统的物流节点时间戳,时间数据的准确性直接决定业务逻辑的可靠性。MySQL作为主流关系型数据库,其日期时间类型的…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

安宝特方案丨XRSOP人员作业标准化管理平台:AR智慧点检验收套件
在选煤厂、化工厂、钢铁厂等过程生产型企业,其生产设备的运行效率和非计划停机对工业制造效益有较大影响。 随着企业自动化和智能化建设的推进,需提前预防假检、错检、漏检,推动智慧生产运维系统数据的流动和现场赋能应用。同时,…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...

第 86 场周赛:矩阵中的幻方、钥匙和房间、将数组拆分成斐波那契序列、猜猜这个单词
Q1、[中等] 矩阵中的幻方 1、题目描述 3 x 3 的幻方是一个填充有 从 1 到 9 的不同数字的 3 x 3 矩阵,其中每行,每列以及两条对角线上的各数之和都相等。 给定一个由整数组成的row x col 的 grid,其中有多少个 3 3 的 “幻方” 子矩阵&am…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

算法笔记2
1.字符串拼接最好用StringBuilder,不用String 2.创建List<>类型的数组并创建内存 List arr[] new ArrayList[26]; Arrays.setAll(arr, i -> new ArrayList<>()); 3.去掉首尾空格...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
