挑战你的数据结构技能:复习题来袭【6】
1. (单选题)设无向图的顶点个数为n,则该图最多有()条边
A. n-1
B. n(n-1)/2
C. n(n+1)/2
D. 0
答案:B
分析:

2. (单选题)含有n个顶点的连通无向图,其边的个数至少为()。
A. n-1
B. n
C. n+1
D. nlog2n
答案:A
分析:
在一个连通无向图中,至少需要有足够的边将所有顶点连接起来,使得图是连通的。这种情况下,最典型的结构是树。树是一种特殊的连通无向图,树具有以下性质:
- **树的顶点数为 n。
- **树的边数为 n-1。
因此,一个含有n个顶点的连通无向图,若它是最小连通信(一般是围充分离化为树结构),则它的边数至少为 n-1。
3. (单选题)()的邻接矩阵是对称矩阵。
A. 有向图
B. 无向图
C. AOV网
D. AOE网
答案:B
分析:
邻接矩阵是否对称取决于图的属性:
-
有向图(Directed Graph):在这种图中,边有方向,即从一个顶点指向另一个顶点。因此,顶点 到顶点 有一条边与顶点 到顶点 有一条边是两种不同的情况,其邻接矩阵一般不对称。
-
无向图(Undirected Graph):在这种图中,边没有方向,因此顶点 与顶点 之间有一条边即顶点 与顶点 之间也有一条边。其邻接矩阵是对称矩阵。
-
AOV网(Activity on Vertex network)和 AOE网(Activity on Edge network):这两种表示的是带权有向图的一种特例,同样其邻接矩阵不对称,因为有方向。
4. (单选题)无向图G=(V,E),其中:V={a, b, c, d,e,f },E={(a,b),(a,e),(a,c),(b, e),(c,f),(f,d),(e,d)},以顶点a为源点,对该图进行深度优先遍历,得到的顶点序列正确的是()。
A. a,b,e,c,d,f
B. a,c,f,e,b,d
C. a,e,b,c,f,d
D. a,e,d,f,c,b
答案:D
5. (单选题)在有向图G的拓扑序列中,若顶点Vi 在顶点Vj 之前,则下列情形不可能出现的是()。
A. G中有边<Vi ,Vj>
B. G中有一条从Vi 到Vj 的路径
C. G中没有边<Vi ,Vj>
D.G中有一条从Vj 到Vi 的路径
答案:D
分析:如果在拓扑排序中 Vi在Vj之前,那么在原图中不应存在从Vj到Vi的路径,否则会形成一个环,无法进行拓扑排序。
6. (单选题)带权有向图G用邻接矩阵A存储,则顶点i的入度等于A中()。
A. 第 i 行非∞的元素之和
B.第 i 列非∞的元素之和
C. 第 i 行非∞且非0元素个数
D. 第 i 列非∞且非0元素个数
答案:D
分析:

7. (单选题)图的深度优先遍历算法类似于二叉树的()算法。
A. 先序遍历
B.中序遍历
C.后序遍历
D.层次遍历
答案:A
分析:
图的深度优先遍历(Depth-First Search, DFS)算法的思想是尽可能深地探索每条边,直到不可能再继续为止,然后回溯。这与二叉树的先序遍历(Preorder Traversal)非常相似。
在二叉树的先序遍历中,遍历的顺序是:
- 访问根节点
- 递归地先序遍历左子树
- 递归地先序遍历右子树
深度优先遍历(DFS)同样是先访问一个节点,然后递归地访问其相邻节点,尝试尽可能深入地进行访问。这种方式和二叉树的先序遍历是具有相同的思路和顺序的。
与其他遍历方法的比较:
- 中序遍历:左子树 -> 根节点 -> 右子树(但图结构没有明确的左右子树之分)
- 后序遍历:左子树 -> 右子树 -> 根节点
- 层次遍历:按层次逐层访问节点(类似广度优先遍历)
8. (单选题)一个有向图G的邻接表存储结构如图所示,现按深度优先搜索遍历,从1出发,所得到的顶点序列是()。

A. 1,2,3,4,5
B. 1,2,3,5,4
C. 1,2,4,5,3
D. 1,2,5,3,4
答案:B
9. (单选题)对如图所示的图进行从顶点1开始的广度优先搜索遍历,可得到的顶点访问序列为()。

A. 1,3,2,4,5,6,7
B. 1,2,4,3,5,6,7
C. 1,2,3,4,5,7,6
D. 2,5,1,4,7,3,6
答案:A
10. (单选题)对于含有n个顶点的带权连通图,它的最小生成树是指图中任意一个( )。
A. 由n-1条权值最小的边构成的子图
B. 由n-1条权值之和最小的边构成的子图
C. 由 n-1条权值之和最小的边构成的连通子图
D. 由n个顶点构成的边的权值之和最小的连通子图
答案:D
11. (单选题)下列关于图的叙述中,正确的是()。
a:回路是简单路径
b:存储稀疏图,用邻接矩阵比邻接表更省空间
c:若有向图中存在拓扑序列,则该图不存在回路
A. 仅a
B. 仅a,b
C. 仅c
D. 仅a,c
答案:C
分析:
a:回路是简单路径
- 这是错误的。简单路径是指路径中没有重复顶点的路径,而回路是起点和终点相同的路径,且路径中顶点可以重复使用。因此,回路并不一定是简单路径。

c:若有向图中存在拓扑序列,则该图不存在回路
- 这是正确的。如果一个有向图有拓扑序列,那么它必须是有向无环图(DAG),这意味着图中不存在回路,否则无法构成拓扑序列。
综上所述,正确的叙述只有选项 c。
12. (单选题)若用邻接矩阵存储有向图,矩阵中主对角线以下的元素均为零,则关于该图拓扑序列的结论是()。
A. 存在,且唯一
B. 存在,且不唯一
C. 存在,可能不唯一
D. 无法确定是否存在
答案:C
分析:

13. (单选题)对如图所示的有向带权图,若采用迪杰斯特拉算法求从源点 a到其他各顶点的最短路径,则得到的第一条最短路径的目标顶点是 b,第二条最短路径的目标顶点是c,后续得到的其余各最短路径的目标顶点依次是()。
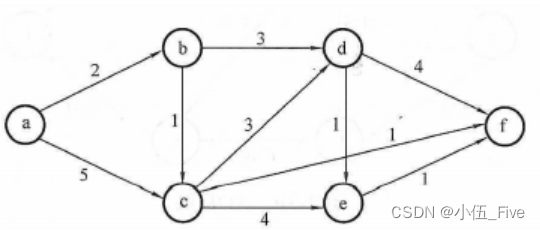
A. d、e、 f
B. e、d、f
C. f、 d、e
D. f、 e、d
答案:C
14. (单选题)
下列关于最小生成树的叙述中,正确的是( )。
Ⅰ.最小生成树的代价唯一
Ⅱ.所有权值最小的边一定会出现在所有的最小生成树中
Ⅲ.使用普里姆算法从不同顶点开始得到的最小生成树一定相同
Ⅳ.使用普里姆算法和克鲁斯卡尔算法得到的最小生成树总不相同
A. 仅Ⅰ
B. 仅Ⅱ
C. 仅Ⅰ、Ⅲ
D. 仅Ⅱ、Ⅳ
答案:A
15. (多选题)一个有n个结点的无向图,最少有()个连通分量,最多有()个连通分量。
A. 0
B. 1
C. n-1
D. n
答案:BD
分析:
在一个有n个节点的无向图中:
-
最少有 1 个连通分量。这是因为无论图中的边怎么分布,只要图中有节点,至少有 1 个连通分量(即整个图本身一块,图不可能没有节点)。所以图的最少连通分量是 1。
-
最多有n个连通分量。这是在每个节点都没有边连接其他节点的情况下,每个节点形成一个单独的连通分量,因此最多有n个连通分量。
16. (多选题)()方法可以判断出一个有向图是否有环。
A. 深度优先遍历
B. 拓扑排序
C. 求最短路径
D. 求关键路径
答案:AB
分析:
判断一个有向图是否有环的常用方法是:
A. 深度优先遍历:在深度优先遍历(DFS)的过程中,可以检测是否存在回边(即从当前节点访问已经在当前遍历路径中的节点)。如果存在回边,则说明图中存在环。
B. 拓扑排序:如果一个有向图可以进行拓扑排序,那么这个图是无环的(即有向无环图,DAG)。反过来,如果一个图不能进行完整的拓扑排序(即过程中某些节点无法加入排序),则说明图中存在环。
C. 求最短路径和D. 求关键路径通常用于计算路径长度或优化路径,不能直接用于判断有向图中是否存在环。
相关文章:

挑战你的数据结构技能:复习题来袭【6】
1. (单选题)设无向图的顶点个数为n,则该图最多有()条边 A. n-1 B. n(n-1)/2 C. n(n1)/2 D. 0 答案:B 分析: 2. (单选题)含有n个顶点的连通无向图,其边的个数至少为()。 A. n-1 B. n C. n1 D. nlog2n 答案:A…...

如何反编译jar并修改后还原为jar
如何反编译jar并修改后还原为jar 目标:修改jar包中某个类的某个方法后还原为新的jar 1.新建android工程,把旧的jar添加为lib 2.用jadx-gui打开旧的jar并保存所有资源 3.找到保存的资源中想修改的.java类 4.复制类中的内容, 在android工程中新建一个同样路径的包,并在包下创建…...
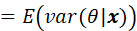
统计信号处理基础 习题解答10-5
题目 通过令 并进行计算来重新推导MMSE估计量。提示:利用结果 解答 首先需要明确的是: 上式是关于观测值x 的函数 其次需要说明一下这个结果 和教材一样,我们用求期望,需要注意的是,在贝叶斯情况下,是个…...
—从零开始:一步步搭建Vue 3自定义插件)
Vue3实战笔记(60)—从零开始:一步步搭建Vue 3自定义插件
文章目录 前言一、自定义插件二、使用步骤总结 前言 在开发和学习中,经常使用一些好用的插件,那么如何创建一个自己的插件呢?在 Vue 3 中,你可以通过创建一个包含 install 方法的对象来定义自定义插件。install 方法接收两个参数…...

Java面向对象笔记
多态 一种类型的变量可以引用多种实际类型的对象 如 package ooplearn;public class Test {public static void main(String[] args) {Animal[] animals new Animal[2];animals[0] new Dog();animals[1] new Cat();for (Animal animal : animals){animal.eat();}} }class …...
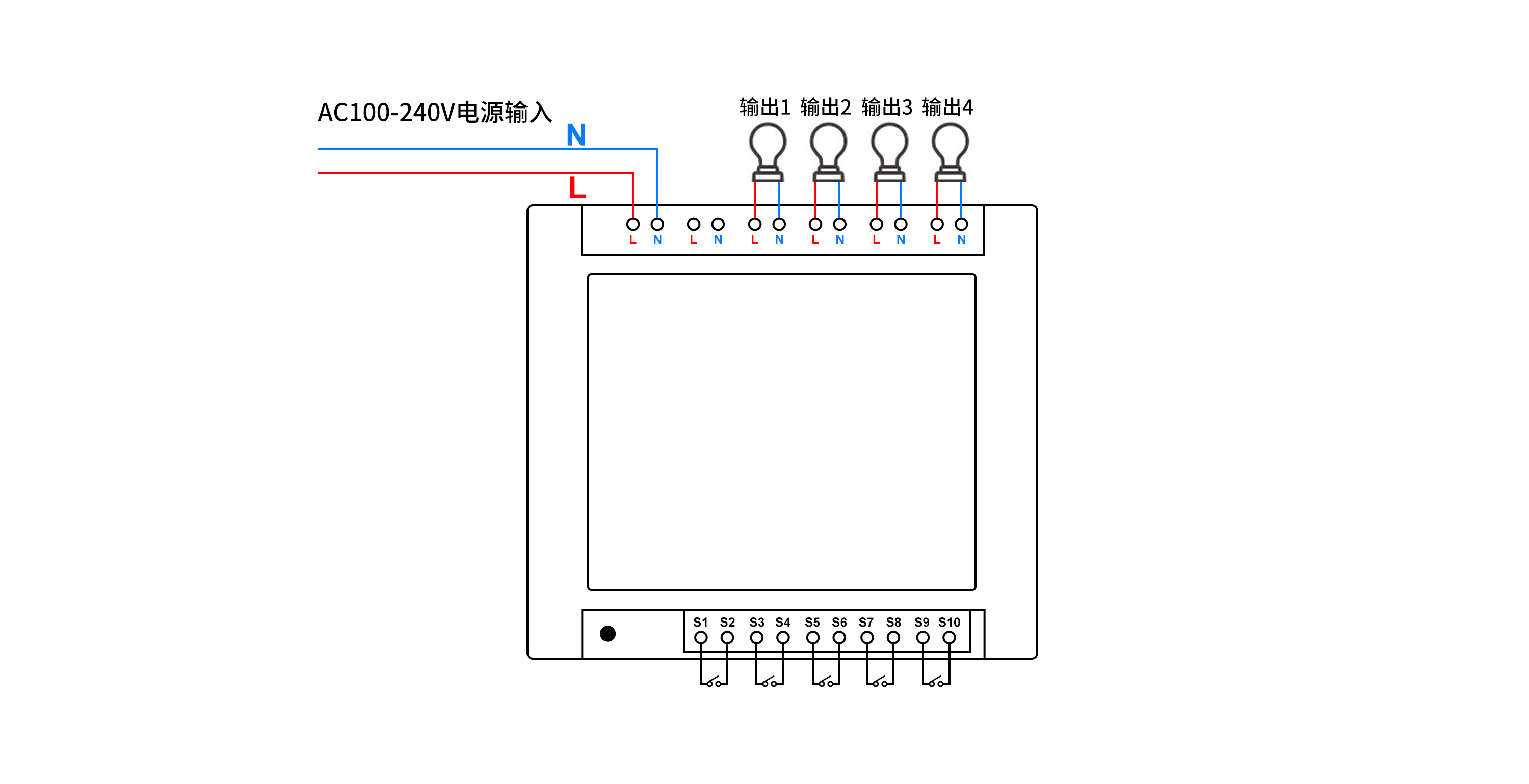
如何通过PHP语言实现远程控制多路照明
如何通过PHP语言实现远程控制多路照明呢? 本文描述了使用PHP语言调用HTTP接口,实现控制多路照明,通过多路控制器,可独立远程控制多路照明。 可选用产品:可根据实际场景需求,选择对应的规格 序号设备名称厂…...

Capture One Pro 23:专业 Raw 图像处理的卓越之选
在当今的数字摄影时代,拥有一款强大的图像处理软件至关重要。而 Capture One Pro 23 for Mac/Win 无疑是其中的佼佼者,为摄影师和图像爱好者带来了前所未有的体验。 Capture One Pro 23 以其出色的 Raw 图像处理能力而闻名。它能够精准地解析和处理各种…...

【主题广泛|投稿优惠】2024年交通运输与信息科学国际会议(ICTIS 2024)
2024年交通运输与信息科学国际会议(ICTIS 2024) 2024 International Conference on Transportation and Information Science 【重要信息】 大会地点:青岛 大会官网:http://www.icictis.com 投稿邮箱:icictissub-conf.…...
表格误删数据保存关闭后如何恢复?5个恢复方法大公开!
“我在编辑表格的时候一不小心就删除了部分数据,现在真的不知道该怎么操作了。希望大家能帮帮我吧!” 在日常工作中,我们经常会使用到各种表格软件来处理和分析数据。然而,有时由于操作失误或其他原因,我们可能会误删表…...

Go 语言中的切片:灵活的数据结构
切片(slice)是 Go 语言中一种非常重要且灵活的数据结构,它提供了对数组子序列的动态窗口。这使得切片在 Go 中的使用非常频繁,特别是在处理动态数据集时。本文将探讨切片的概念、操作和与函数的交互,以及如何有效地使用…...
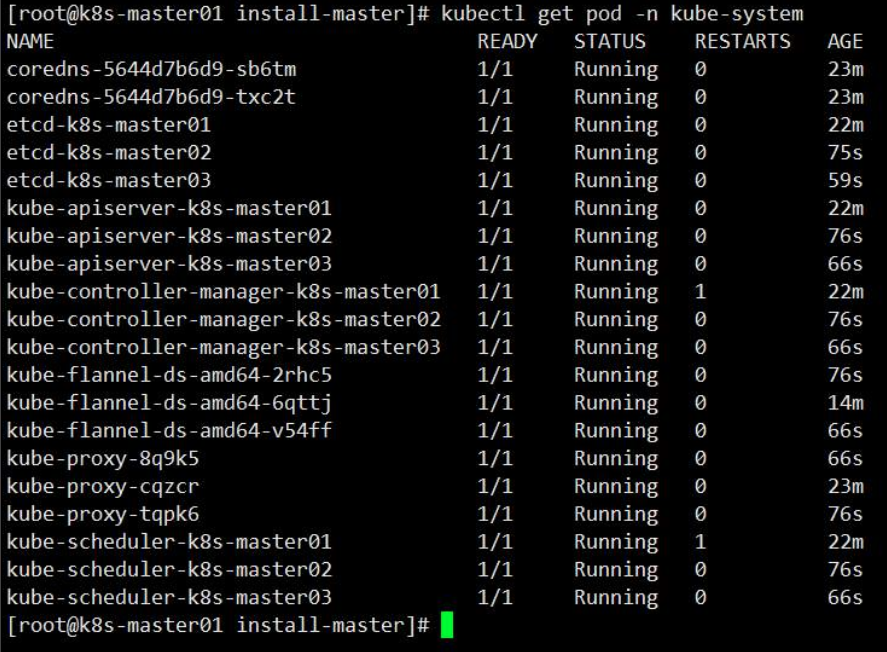
在鲲鹏服务器搭建k8s高可用集群分享
高可用架构 本文采用kubeadm方式搭建k8s高可用集群,k8s高可用集群主要是对apiserver、etcd、controller-manager、scheduler做的高可用;高可用形式只要是为: 1. apiserver利用haproxykeepalived做的负载,多apiserver节点同时工作…...
)
MySQL之数据库事务机制学习笔记(五)
事务机制 事务(Transaction)是数据库管理系统中的一个重要概念,它是一组数据库操作的逻辑单元,要么全部执行成功,要么全部执行失败,具有以下四个特性,通常缩写为 ACID: 原子性&…...

linux 系统被异地登录,cpu占用拉满100%
一般是kswapd0导致的cpu占用异常 按顺序执行以下操作 在控制台执行top命令,查看占用最高的是否kswapd0。基本100%占用。记下该进程ID 5081 执行查找命令 find / -name kswapd0 显示查找结果: /proc/3316/.X2c4-unix/.rsync/a/kswapd0 /root/.configrc…...
智慧校园应用平台的全面建设
在当今社会,随着科技的不断进步,智慧校园应用平台逐渐成为学校管理的必备工具。在实现智慧校园全面建设的过程中,学校需要运用先进的技术和创新的理念,为教育提供更好的服务和支持。这篇文章将为您介绍智慧校园应用平台的全面建设…...

图论第6天
提高效率!!!两道题看并查集 841.钥匙和房间 忘了把visited 加引用了:& class Solution { public:bool canVisitAllRooms(vector<vector<int>>& rooms) {vector<int>visited(rooms.size(),false);dfs(rooms,visited,0);for(int i 0;i …...
:Redis怎么保证缓存一致性)
Redis教程(二十一):Redis怎么保证缓存一致性
传送门:Redis教程汇总篇,让你从入门到精通 Redis 的缓存一致性 Redis 的缓存一致性是指在使用 Redis 作为缓存层时,保证缓存中的数据与数据库中的数据保持一致的状态。在分布式系统中,数据一致性是一个重要的问题,因为可能存在多个客户端同时读写同一数据,或者数据在不同…...

android apk签名
android apk签名 命令: java -jar signapk.jar platform.x509.pem platform.pk8 **.apk ***.apk note: apk密钥为: platform.pk8和platform.x509.pem 路径: build\target\product\security apk签名工具:sign…...

flutter 解析json另类封装方式 List<bean>,哈哈哈
flutter 解析json另类封装方式,哈哈哈 日常学习,仅供参考,不喜 勿喷 http请求数据泛型解析封装,需要判断泛型数据类型再根据类型解析,本文只抽取了list演示 核心代码 import dart:convert;import package:webwsyn/h…...
)
哈希表(Hash table)
哈希表(Hash table),也称为散列表,是一种根据关键码值(Key value)直接进行访问的数据结构。它通过散列函数(Hash function)将关键码值映射到表中的一个位置,以此来访问记录,从而加快查找的速度。以下是关于哈希表的详细解释: 基本概念 散列函数:将关键码值映射到表…...
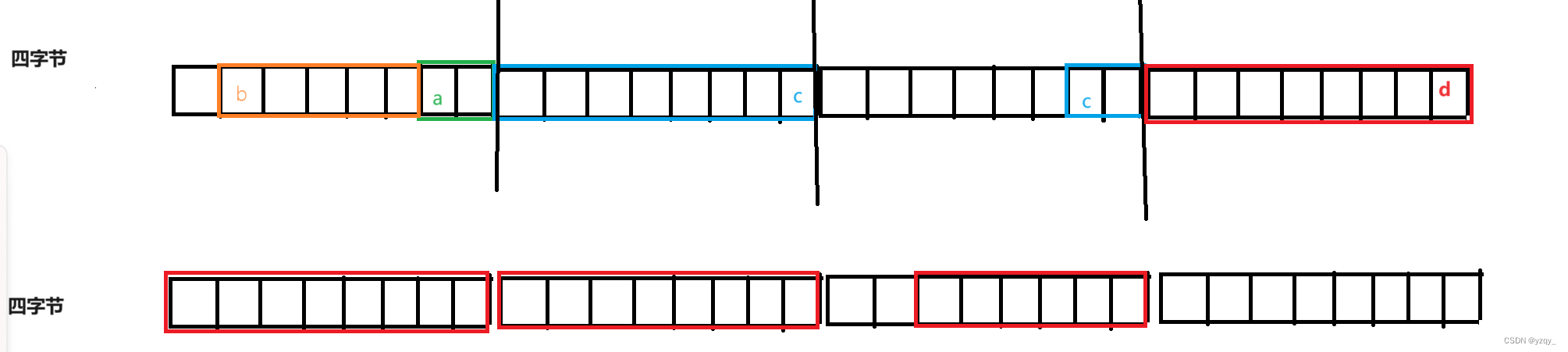
【c语言】自定义类型-结构体
结构体 结构体的声明与使用结构体的声明与初始化结构体的自引用 结构体的内存对齐对齐规则为什么存在内存对齐修改默认对齐数 结构体的传参结构体实现位段什么是位段位段的内存分配位段的跨平台问题位段使用的注意事项 结构体:是一个自定义的类型,成员可…...

java_网络服务相关_gateway_nacos_feign区别联系
1. spring-cloud-starter-gateway 作用:作为微服务架构的网关,统一入口,处理所有外部请求。 核心能力: 路由转发(基于路径、服务名等)过滤器(鉴权、限流、日志、Header 处理)支持负…...

Docker 运行 Kafka 带 SASL 认证教程
Docker 运行 Kafka 带 SASL 认证教程 Docker 运行 Kafka 带 SASL 认证教程一、说明二、环境准备三、编写 Docker Compose 和 jaas文件docker-compose.yml代码说明:server_jaas.conf 四、启动服务五、验证服务六、连接kafka服务七、总结 Docker 运行 Kafka 带 SASL 认…...

无法与IP建立连接,未能下载VSCode服务器
如题,在远程连接服务器的时候突然遇到了这个提示。 查阅了一圈,发现是VSCode版本自动更新惹的祸!!! 在VSCode的帮助->关于这里发现前几天VSCode自动更新了,我的版本号变成了1.100.3 才导致了远程连接出…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

pgsql:还原数据库后出现重复序列导致“more than one owned sequence found“报错问题的解决
问题: pgsql数据库通过备份数据库文件进行还原时,如果表中有自增序列,还原后可能会出现重复的序列,此时若向表中插入新行时会出现“more than one owned sequence found”的报错提示。 点击菜单“其它”-》“序列”,…...

LUA+Reids实现库存秒杀预扣减 记录流水 以及自己的思考
目录 lua脚本 记录流水 记录流水的作用 流水什么时候删除 我们在做库存扣减的时候,显示基于Lua脚本和Redis实现的预扣减 这样可以在秒杀扣减的时候保证操作的原子性和高效性 lua脚本 // ... 已有代码 ...Overridepublic InventoryResponse decrease(Inventor…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...

C#最佳实践:为何优先使用as或is而非强制转换
C#最佳实践:为何优先使用as或is而非强制转换 在 C# 的编程世界里,类型转换是我们经常会遇到的操作。就像在现实生活中,我们可能需要把不同形状的物品重新整理归类一样,在代码里,我们也常常需要将一个数据类型转换为另…...

Shell 解释器 bash 和 dash 区别
bash 和 dash 都是 Unix/Linux 系统中的 Shell 解释器,但它们在功能、语法和性能上有显著区别。以下是它们的详细对比: 1. 基本区别 特性bash (Bourne-Again SHell)dash (Debian Almquist SHell)来源G…...
