【红黑树变色+旋转】
文章目录
- 一. 红黑树规则
- 二. 情况一叔叔存在且为红
- 情况二.变色+旋旋
一. 红黑树规则
对于红黑树,进行变色+旋转处理,终究都是为了维持颜色+以下几条规则,只有颜色和规则维持住了,红黑树就维持住了最长路径的长度不超过最短路径的两倍。
规则:
- 根是黑的。
- 没有连续的红节点。
- 每条路径的黑色数量相等。
二. 情况一叔叔存在且为红
注意点:红黑树插入的节点都是红色的,因为在红黑树中动黑色节点是非常忌讳的,因为要维持每条路径黑色数量相等非常困难,所以插入的节点默认都是红色的。
当插入红色节点后:1.如果父亲为黑或者父亲不存在,结束,不需要任何处理。
2. 如果父亲存在且为红,由于插入节点为红,存在连续红节点,需要处理,可以肯定的是爷爷一定是黑,因为插入节点前就是一棵红黑树了,既然父亲和爷爷颜色确定,主要看叔叔。
1.叔叔存在且为红

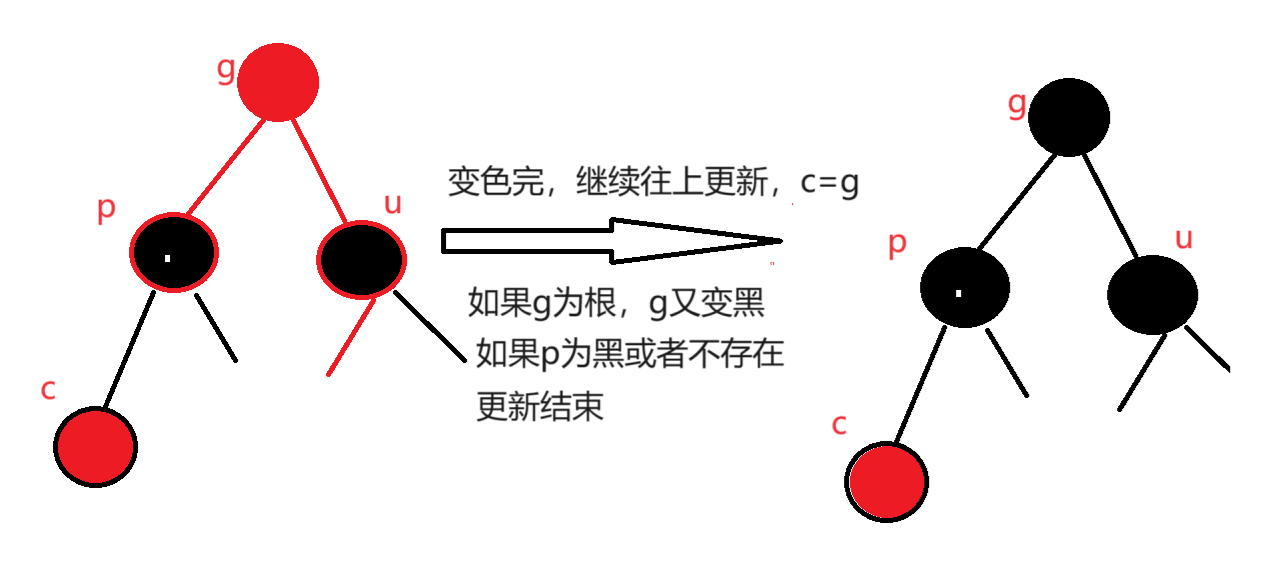
情况二.变色+旋旋
叔叔存在且为黑或者叔叔不存在都需变色+旋转,关键分析是左单旋,右单旋,还是左右双旋,还是右左双旋只要旋转后,就平衡了,直接结束,不需要向上更新
1. 变色+单旋
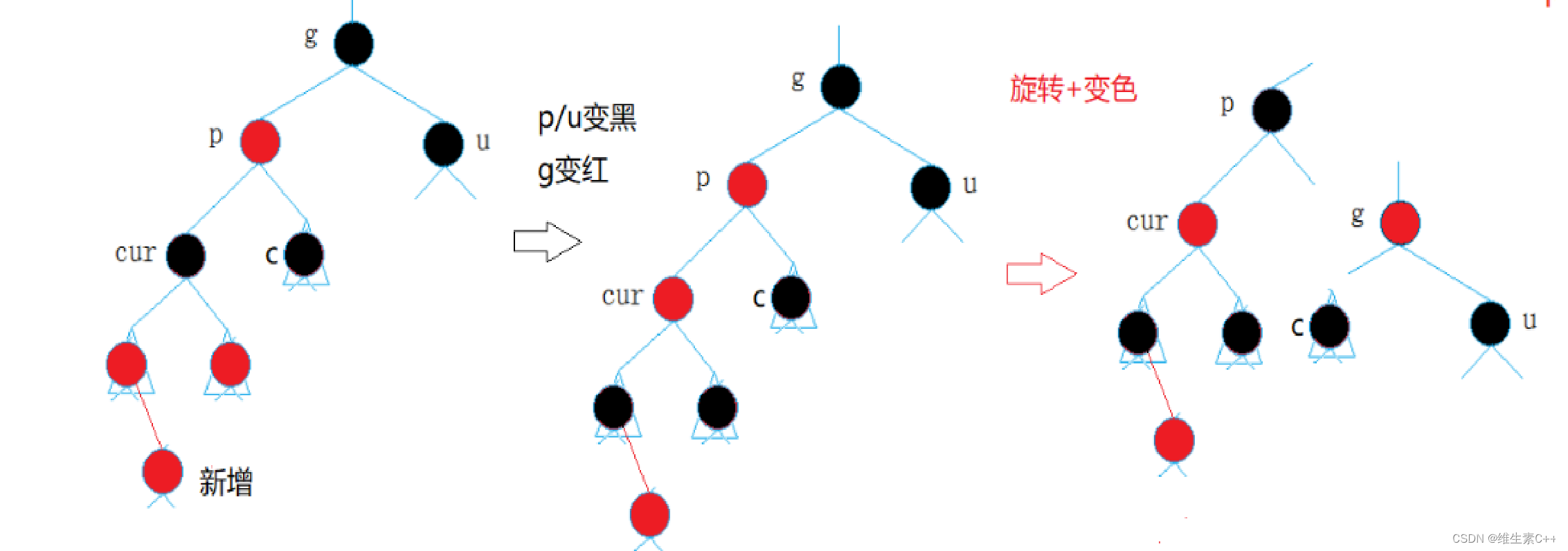
对于叔叔存在且为黑或不存在这种情况,不可能是因为直接插入红色节点导致连续红这种情况直接发生的,因为这发生了,原本就不是红黑树,一定是由上述图一第一种情况处理更新上来导致的。
解决办法:curp->left, pg->left 左左右单旋g点+
p变黑,g变红。
同理:如果上述情况curp->right, pg->right,右右左单旋g点+p变黑,g变红
2.变色+双旋
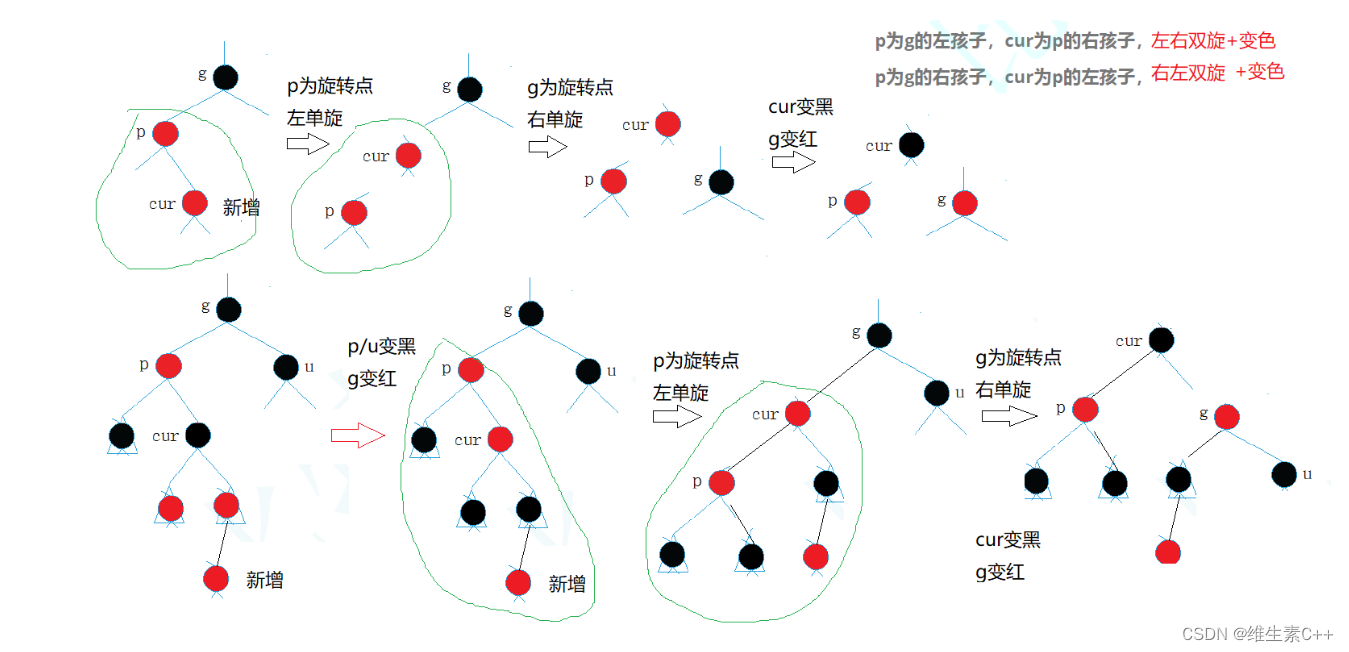
对于这种情况:curp->right, pg->left,左右双旋,
将p左旋,g右旋,+ cur变黑+g变红。
同理:curp->left, pg->right, 右左双旋,将p右旋,g左旋,+cur变黑+g变红
总结单纯变色处理,需要不停向上更新至父亲不存在或者父亲为黑结束,旋转+变色处理完就平衡了直接结束。
一下是代码实现
bool Insert(const pair<K, V>& kv){if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK; //根为黑色return true;}Node* parent = nullptr;Node* cur = _root;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;}}cur = new Node(kv);if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//父亲存在且为红,连续红节点,处理(如果父亲不存在管你红黑就结束了,如果为黑也结束了)while (parent && parent->_col == RED){Node* grandfather = parent->_parent; //算出爷爷,根据父亲为爷爷的左右,确定叔叔if (parent == grandfather->_left){Node* uncle = grandfather->_right;//情况一:叔叔存在且为红 变色处理if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//根节点保证为黑下面处理//继续往上处理cur = grandfather;parent = cur->_parent;}//情况二:叔叔不存在/叔叔存在且为黑else{//需要判别单旋还是左旋,确定cur的位置//旋转+变色if (cur == parent->_left){// g// p u//c//左左右单旋RotateR(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// p u// c//左右双旋+变色RotateL(parent);RotateR(grandfather);cur->_col = BLACK;grandfather->_col = RED;}break; //只要旋转结束就平衡了结束}}else{Node* uncle = grandfather->_left;//情况一:叔叔存在且为红 变色处理if (uncle && uncle->_col == RED){parent->_col = uncle->_col = BLACK;grandfather->_col = RED;//根节点保证为黑下面处理//继续往上处理cur = grandfather;parent = cur->_parent;}//情况二:叔叔不存在/叔叔存在且为黑else{if (cur == parent->_right){// g// u p// cRotateL(grandfather);parent->_col = BLACK;grandfather->_col = RED;}else{// g// u p// c//右左双旋RotateR(parent);RotateL(grandfather);cur->_col = BLACK;grandfather->_col = RED;}//只要旋转完了,就平衡结束了break;}}}_root->_col = BLACK; //变色没有处理根,无论怎么处理都保证根是黑的return true;}void RotateL(Node* parent){++rotateSize;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;if (subRL)subRL->_parent = parent;subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;if (_root == parent){_root = subR;subR->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}}void RotateR(Node* parent){++rotateSize;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;if (subLR)subLR->_parent = parent;subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (parent == ppnode->_left){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}}无论怎么方式处理完都需要保证根是黑的,最后加上
相关文章:

【红黑树变色+旋转】
文章目录 一. 红黑树规则二. 情况一叔叔存在且为红情况二.变色旋旋 一. 红黑树规则 对于红黑树,进行变色旋转处理,终究都是为了维持颜色以下几条规则,只有颜色和规则维持住了,红黑树就维持住了最长路径的长度不超过最短路径的两倍…...

pytorch 使用tensor混合:进行index操作
(Pdb) tmp torch.randn(3,5) (Pdb) indx torch.tensor([1,0]).long() (Pdb) temp(indx) *** NameError: name ‘temp’ is not defined (Pdb) tmp(indx) *** TypeError: ‘Tensor’ object is not callable (Pdb) tmp[indx] tensor([[ 0.1633, 0.9389, 1.2806, -0.2525, 0.28…...
Threejs(WebGL)绘制线段优化:Shader修改gl.LINES模式为gl.LINE_STRIP
目录 背景 思路 Threejs实现 记录每条线的点数 封装原始裁剪索引数据 封装合并几何体的缓冲数据:由裁剪索引组成的 IntArray 守住该有的线段! 修改顶点着色器 修改片元着色器 完整代码 WebGL实现类似功能(简易版,便于测…...

继承-进阶
父子类成员共享 普通成员对象/父子间不共享, 成员独立 函数成员共享(函数不存储在对象中) 子类由两部分构成:父类中继承的成员和子类中新定义成员 继承方式 子类中存在父类private成员但不可直接访问(及时在类中&am…...

探索k8s集群的配置资源(secret和configmap)
目录 ConfigMap ConfigMap(主要是将配置目录或者文件挂载到k8s里面使用) 与Secret类似,区别在于ConfigMap保存的是不需要加密配置的信息。(例如:配置文件) ConfigMap 功能在 Kubernetes1.2 版本中引入&…...

如何设置vue3项目中默认的背景为白色
方法1:通过CSS全局样式 在全局CSS文件中设置: 如果你的项目中有全局的CSS文件(如App.vue或专门的CSS文件),你可以直接设置body或html标签的背景颜色。 在src/assets文件夹中(或者任何你存放CSS文件的地方&a…...

MS1112驱动开发
作者简介: 一个平凡而乐于分享的小比特,中南民族大学通信工程专业研究生在读,研究方向无线联邦学习 擅长领域:驱动开发,嵌入式软件开发,BSP开发 作者主页:一个平凡而乐于分享的小比特的个人主页…...
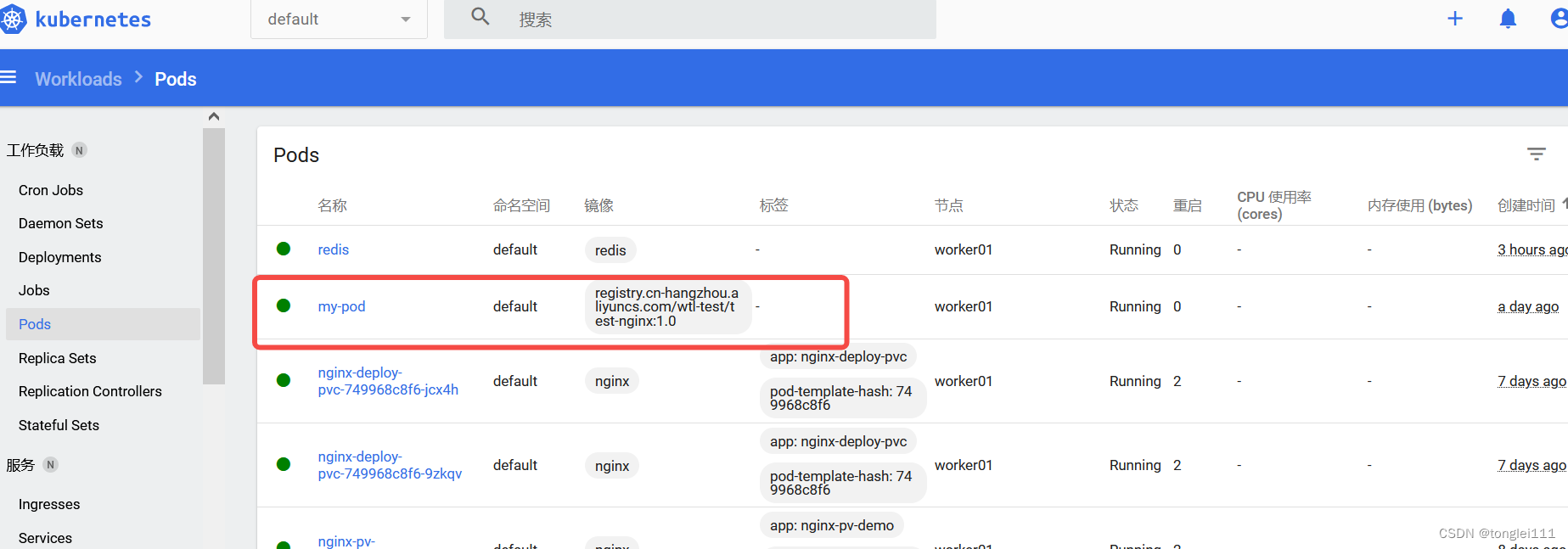
K8s存储对象的使用
背景和概念 容器中的文件在磁盘上是临时存放的,这给在容器中运行较重要的应用带来一些问题: 当容器崩溃或停止时,此时容器状态未保存, 因此在容器生命周期内创建或修改的所有文件都将丢失。另外 在崩溃期间,kubelet 会…...
构建自动化API数据抓取系统
构建一个自动化API数据抓取系统是一个涉及多个技术领域的复杂任务。这样的系统不仅要求高效的数据获取能力,还需要有稳定的数据处理、存储和错误处理机制。 1. 需求分析 在开始构建之前,明确你的需求至关重要。你需要确定要抓取的API、数据的频率、数据的…...
【Qt知识】部分QWidget属性表格
QWidget是Qt库中所有图形用户界面组件的基类,它提供了大量属性以供自定义和配置控件的行为和外观。下面列出了一些主要的QWidget属性及其作用。 属性 作用 accessibleName 控件的辅助技术名称,用于无障碍访问。 accessibleDescription 控件的辅助技…...

【ARM64 常见汇编指令学习 19.1 -- ARM64 跳转指令 b.pl 详细介绍】
文章目录 ARM64 跳转指令 b.pl使用场景语法示例总结 ARM64 跳转指令 b.pl 在 ARMv8 架构中,b.pl 是一条条件分支(Branch)指令,它根据当前的状态寄存器中的条件标志执行跳转。b.pl 的全称是 Branch if Plus,即如果条件…...

WWDC24即将到来,ios18放大招
苹果公司即将在下周开全球开发者大会(WWDC),大会上将展示其人工智能技术整合到设备和软件中的重大进展,包括与OpenAI的历史性合作。随着大会的临近,有关iOS 18及其据称采用AI技术支持的应用程序和功能的各种泄露信息已经浮出水面。 据报道,苹果将利用其自主研发的大…...

C#中的空合并运算符与空合并赋值运算符:简化空值处理
在C#编程中,处理可能为null的值是一项常见的任务,尤其是在涉及数据库查询、Web服务调用或任何可能返回缺失数据的场景中。为了简化这类操作并提高代码的可读性,C# 8 引入了两个非常实用的运算符:空合并运算符 (??) 和 空合并赋值…...

数据结构:哈夫曼树及其哈夫曼编码
目录 1.哈夫曼树是什么? 2.哈夫曼编码是什么? 3.哈夫曼编码的应用 4.包含头文件 5.结点设计 6.接口函数定义 7.接口函数实现 8.哈夫曼编码测试案列 哈夫曼树是什么? 哈夫曼树(Huffman Tree)是一种特殊的二叉树…...
微信如何防止被对方拉黑删除?一招教你解决!文末附软件!
你一定不知道,微信可以防止被对方拉黑删除,秒变无敌。只需一招就能解决!赶快来学!文末有惊喜! 惹到某些重要人物(比如女朋友),被删除拉黑一条龙,那真的是太令人沮丧了&a…...

jar增量打包
jar增量打包 Linux环境下: 1.解压缩 jar -xvf jarname.jar(解压)2.打包 这时可以把要替换的lib包的内容粘帖进去,然后重新打jar包 jar -cvf0M jarname.jar .(重新压缩,-0是主要的)jar命令: …...

智慧医院物联网建设-统一管理物联网终端及应用
近年来,国家卫健委相继出台的政策和评估标准体系中,都涵盖了强化物联网建设的内容。物联网建设已成为智慧医院建设的核心议题之一。 作为医院高质量发展的关键驱动力,物联网的顶层设计与网络架构设计规划,既需要结合现代信息技术的…...

Debian的常用命令
Debian作为一个稳定、安全且高效的Linux发行版,被广泛应用于服务器和桌面操作系统中。对于系统管理员和开发者来说,熟练掌握Debian的常用命令能够大大提升工作的效率和系统的管理水平。本文将详细介绍一些常见且实用的Debian命令,帮助新手更好地管理和操作Debian系统。 系统…...

矩阵1-范数与二重求和的求和可交换
矩阵1-范数与二重求和的求和可交换 1、矩阵1-范数 A [ a 11 a 12 ⋯ a 1 n a 21 a 22 ⋯ a 2 n ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ⋯ a n n ] A \begin{bmatrix} a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots …...

Python笔记 - *args和**kwargs
探索Python的*args和**kwargs 在Python中,函数可以接受任意数量的参数,而这要归功于*args和**kwargs的强大功能。这两个特性使得函数在处理不同数量的输入时变得更加灵活和高效。在这篇博客中,我们将详细介绍*args和**kwargs,并展…...

SpringBoot-17-MyBatis动态SQL标签之常用标签
文章目录 1 代码1.1 实体User.java1.2 接口UserMapper.java1.3 映射UserMapper.xml1.3.1 标签if1.3.2 标签if和where1.3.3 标签choose和when和otherwise1.4 UserController.java2 常用动态SQL标签2.1 标签set2.1.1 UserMapper.java2.1.2 UserMapper.xml2.1.3 UserController.ja…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

Linux云原生安全:零信任架构与机密计算
Linux云原生安全:零信任架构与机密计算 构建坚不可摧的云原生防御体系 引言:云原生安全的范式革命 随着云原生技术的普及,安全边界正在从传统的网络边界向工作负载内部转移。Gartner预测,到2025年,零信任架构将成为超…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材)
推荐 github 项目:GeminiImageApp(图片生成方向,可以做一定的素材) 这个项目能干嘛? 使用 gemini 2.0 的 api 和 google 其他的 api 来做衍生处理 简化和优化了文生图和图生图的行为(我的最主要) 并且有一些目标检测和切割(我用不到) 视频和 imagefx 因为没 a…...
详细解析)
Caliper 负载(Workload)详细解析
Caliper 负载(Workload)详细解析 负载(Workload)是 Caliper 性能测试的核心部分,它定义了测试期间要执行的具体合约调用行为和交易模式。下面我将全面深入地讲解负载的各个方面。 一、负载模块基本结构 一个典型的负载模块(如 workload.js)包含以下基本结构: use strict;/…...

MySQL体系架构解析(三):MySQL目录与启动配置全解析
MySQL中的目录和文件 bin目录 在 MySQL 的安装目录下有一个特别重要的 bin 目录,这个目录下存放着许多可执行文件。与其他系统的可执行文件类似,这些可执行文件都是与服务器和客户端程序相关的。 启动MySQL服务器程序 在 UNIX 系统中,用…...

深度解析云存储:概念、架构与应用实践
在数据爆炸式增长的时代,传统本地存储因容量限制、管理复杂等问题,已难以满足企业和个人的需求。云存储凭借灵活扩展、便捷访问等特性,成为数据存储领域的主流解决方案。从个人照片备份到企业核心数据管理,云存储正重塑数据存储与…...
