几何关系运算处理
1. 判断点在线的左边还是右边
要判断一个坐标点在直线的左侧还是右侧,可以使用向量叉积。具体来说,对于给定的直线和点,我们可以计算点到直线的向量与直线的方向向量的叉积。叉积的符号可以用于判断点的位置关系:
- 如果叉积为正,则点在直线的左侧。
- 如果叉积为负,则点在直线的右侧。
- 如果叉积为零,则点在直线上。
示例代码
import numpy as np
from shapely.geometry import Point, LineStringdef is_point_left_of_line(point, line_start, line_end):"""判断点是否在直线的左侧。:param point: 待判断的点 (x, y):param line_start: 直线的起点 (x, y):param line_end: 直线的终点 (x, y):return: >0 表示点在左侧, <0 表示点在右侧, =0 表示点在直线上"""px, py = pointx1, y1 = line_startx2, y2 = line_end# 计算向量v1 = np.array([x2 - x1, y2 - y1])v2 = np.array([px - x1, py - y1])# 计算向量叉积cross_product = np.cross(v1, v2)return cross_product# 示例点和直线
point = (3, 3)
line_start = (1, 1)
line_end = (5, 2)result = is_point_left_of_line(point, line_start, line_end)if result > 0:print("点在直线的左侧")
elif result < 0:print("点在直线的右侧")
else:print("点在直线上")
代码说明
-
向量计算:
- 计算从直线起点到终点的向量
v1。 - 计算从直线起点到点的向量
v2。
- 计算从直线起点到终点的向量
-
叉积计算:
- 计算向量
v1和v2的叉积。 - 叉积的符号可以判断点的位置关系:正值表示点在左侧,负值表示点在右侧,零表示点在直线上。
- 计算向量
示例结果
对于给定的示例点 (3, 3) 和直线 (1, 1) 到 (5, 2):
- 如果输出 "点在直线的左侧",则表示点
(3, 3)在直线(1, 1)到(5, 2)的左侧。 - 如果输出 "点在直线的右侧",则表示点
(3, 3)在直线(1, 1)到(5, 2)的右侧。 - 如果输出 "点在直线上",则表示点
(3, 3)在直线(1, 1)到(5, 2)上。
这个方法可以用于各种几何判断和路径规划问题,确保对点的位置关系有准确的判断
相关文章:

几何关系运算处理
1. 判断点在线的左边还是右边 要判断一个坐标点在直线的左侧还是右侧,可以使用向量叉积。具体来说,对于给定的直线和点,我们可以计算点到直线的向量与直线的方向向量的叉积。叉积的符号可以用于判断点的位置关系: 如果叉积为正&…...

http和https分别是什么?区别是什么?
HTTP和HTTPS是两种常见的网络协议,用于在Web上进行数据传输。以下是它们的简要解释和主要区别: HTTP(Hypertext Transfer Protocol) HTTP是一种应用层协议,用于在Web上传输数据。它是互联网上应用最为广泛的一种网络…...
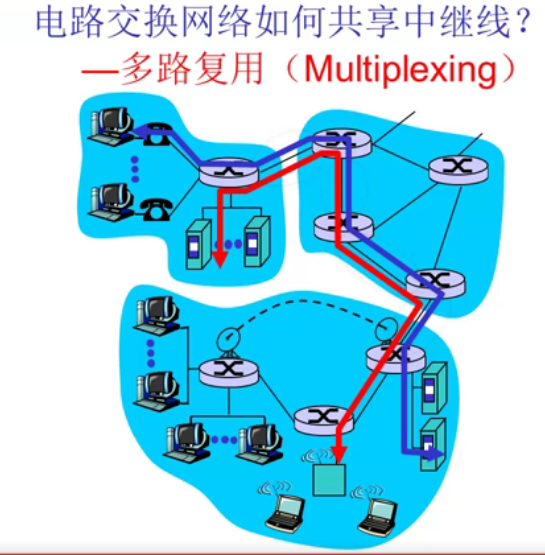
第一周:计算机网络概述(上)
一、计算机网络基本概念 1、计算机网络通信技术计算机技术 计算机网络就是一种特殊的通信网络,其特殊之处就在于它的信源和信宿就是计算机。 2、什么是计算机网络 在计算机网络中,我们把这些计算机统称为“主机”(上图中所有相连的电脑和服…...

谷歌AI搜索变革,中国引擎能跟上步伐?
全文预计1200字左右,预计阅读需要6分钟。 一年前,谷歌宣布人工智能将引领搜索的未来,如今,这一愿景正逐步实现。谷歌已在美国推出并即将全球推广"AI Overviews",为用户提供由AI生成的搜索结果概览࿰…...
【机器学习300问】110、什么是Lasso回归模型?
LASSO回归的全称是Least Absolute Shrinkage and Selection Operator,中文叫“最小绝对收缩和选择算子”,用一个比喻来初步感受一下它的作用: 想象你在整理一个杂乱无章的房间,里面堆满了各种物品(代表众多的预测变量&…...

Qt实现麦克风音频输入保存wav文件
一.本文目的 实现在Qt中接收麦克风数据并保存为WAV文件,使用QAudioInput来录音,并使用QFile来保存数据到WAV文件。 开发环境:QT5.12 本文用极简代码实现,核心代码只需不到100行。 完整工程代码文末链接可以直接下载。 二.代码实…...
)
docker_如何推送镜像到仓库(hub.docker.com)
在执行 docker push 时收到 denied: requested access to the resource is denied 错误通常意味着你没有权限将镜像推送到目标存储库。这可能有几个原因,包括: 未登录 Docker Hub:你还没有登录到 Docker Hub,或者你登录的账户没有权限推送到目标存储库。存储库不存在:目标…...

【Python】认识 Python
一、计算机基础概念 1、什么是计算机 很多老一辈的人,管下面这个叫做计算机。然而,它只是 “计算器”,和计算机是有很大区别的。 现在我们所说的计算机,不光能进行算术运算,还能进行逻辑判断、数据存储、网络通信等…...

Vue根据后端返回的tabList动态渲染组件信息
最近做了一个功能,后端根据配置信息,动态返回一个tabList,其中结构是List<String,Object> tabList; map里面的数据是 label、value 页面需要根据tablist动态渲染组件(不同的tab都使用了组件进行了封装) 实现效果…...

二轴机器人大米装箱机:技术创新引领智能包装新潮流
在科技日新月异的今天,自动化和智能化已成为各行各业追求高效、精准生产的关键。作为粮食加工行业的重要一环,大米装箱机的技术创新与应用价值日益凸显。其中,二轴机器人大米装箱机以其高效、稳定、智能的特点,成为市场的新宠。星…...
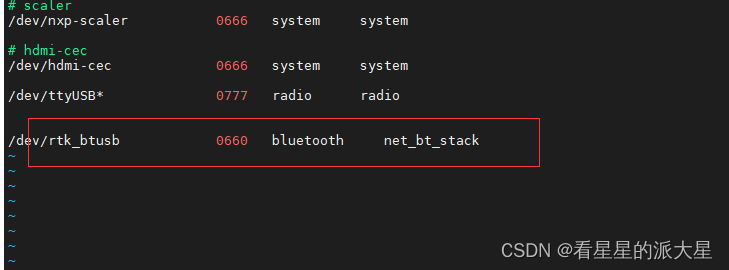
rtl8723DU移植 android4.4 4418 (第二部分蓝牙部分)
使用的代码: HMI (8723bu)源码 567_RTL8723DU_WiFi_linux_v5.6.5.3_35502_COEX20181130-2e2e.20191025.zip 由于之前写的所有笔记没有保存,这里只能是部分。 0、 前置知识 1 、kernel 的移植 2、hardwire的移植 将 驱动中的 h…...
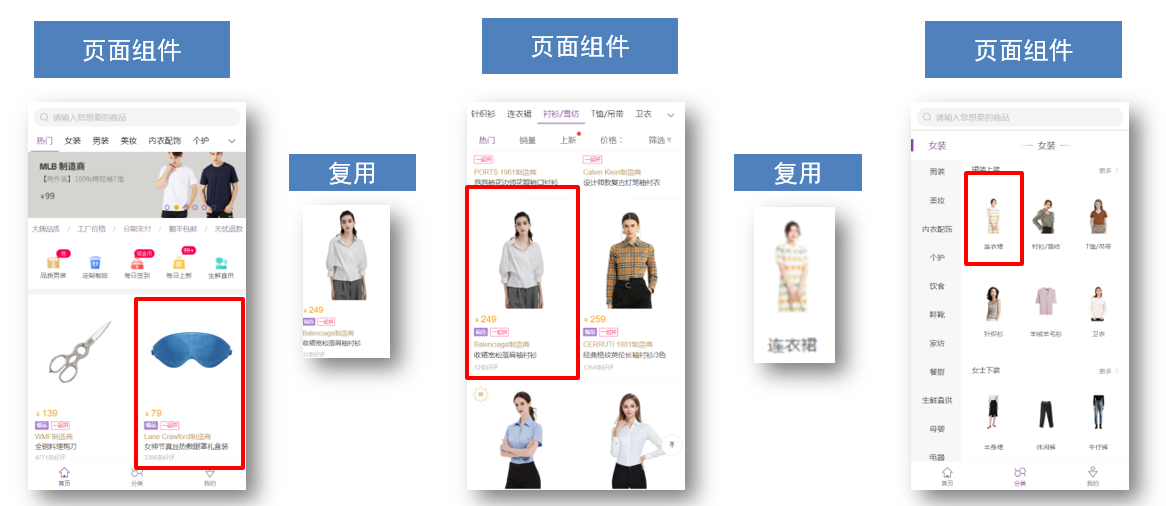
【Vue】组件的存放目录问题
注意: .vue文件 本质无区别 组件分类 .vue文件分为2类,都是 .vue文件(本质无区别) 页面组件 (配置路由规则时使用的组件)复用组件(多个组件中都使用到的组件) 存放目录 分类开来的…...

开发PlugLink插件:自动生成并发布博客文章
开发PlugLink插件:自动生成并发布博客文章 引言 博客已经成为个人和企业分享信息、推广产品的重要工具。然而,手动运营博客不仅耗时,而且容易出错。本文将介绍如何利用PlugLink开发一个全自动博客运营程序,通过API链接大模型&am…...
Ant Design Pro
一:Ant Design pro是什么: Ant Design Pro 是基于 Ant Design 和 umi 的封装的一整套企业级中后台前端/设计解决方案,致力于在设计规范和基础组件的基础上,继续向上构建,提炼出典型模板/业务组件/配套设计资源&#x…...

加密软件好用的是哪个?为什么这么多人说迅软DSE加密软件好用?
加密软件顾名思义就是用来对机密文件进行加密保护的,防止未经授权的人查看和篡改,保护公司的重要信息,预防泄露的事件发生,由此可见运用加密软件是有用的。那么,问题又来了哪款加密软件好呢?请看一下介绍。…...

大模型日报2024-06-07
大模型日报 2024-06-07 大模型资讯 大规模单细胞转录组学基础模型研究 摘要: 大型预训练模型已成为基础模型,在自然语言处理及相关领域取得突破。本文介绍了在单细胞转录组学领域应用大规模基础模型的研究进展。 MMLU-Pro:评估语言理解模型的新基准 摘要…...
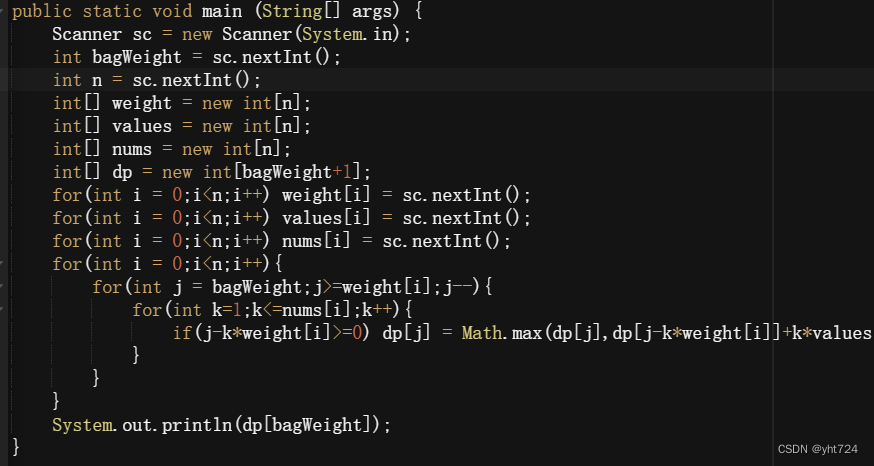
Day49 动态规划part08
LC139单词拆分(未掌握) 未掌握分析:将字符串s中的各个字符看成是背包,思考成了多重背包问题单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。拆分时可以重复使用字典中的单词…...
React -- memo允许你的组件在 props 没有改变的情况下跳过重新渲染。
memo(Component, arePropsEqual?) 使用 memo 将组件包装起来,以获得该组件的一个 记忆化 版本。通常情况下,只要该组件的 props 没有改变,这个记忆化版本就不会在其父组件重新渲染时重新渲染。但 React 仍可能会重新渲染它:记忆化…...

路径
自学python如何成为大佬(目录):https://blog.csdn.net/weixin_67859959/article/details/139049996?spm1001.2014.3001.5501 用于定位一个文件或者目录的字符串被称为一个路径。在程序开发时,通常涉及两种路径,一种是相对路径,另一种是绝对…...

逆波兰表达式
目录 一、定义 二、算法步骤 三、代码实现 一、定义 逆波兰表达式又叫做后缀表达式,是一种没有括号,并严格遵循“从左到右”运算的后缀式表达方法。 二、算法步骤 1、首先构造一个运算符栈,此运算符在栈内遵循越往栈顶优先级越高的原则。 …...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...
)
Spring Boot 实现流式响应(兼容 2.7.x)
在实际开发中,我们可能会遇到一些流式数据处理的场景,比如接收来自上游接口的 Server-Sent Events(SSE) 或 流式 JSON 内容,并将其原样中转给前端页面或客户端。这种情况下,传统的 RestTemplate 缓存机制会…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析
Java求职者面试指南:Spring、Spring Boot、MyBatis框架与计算机基础问题解析 一、第一轮提问(基础概念问题) 1. 请解释Spring框架的核心容器是什么?它在Spring中起到什么作用? Spring框架的核心容器是IoC容器&#…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Python竞赛环境搭建全攻略
Python环境搭建竞赛技术文章大纲 竞赛背景与意义 竞赛的目的与价值Python在竞赛中的应用场景环境搭建对竞赛效率的影响 竞赛环境需求分析 常见竞赛类型(算法、数据分析、机器学习等)不同竞赛对Python版本及库的要求硬件与操作系统的兼容性问题 Pyth…...

JDK 17 序列化是怎么回事
如何序列化?其实很简单,就是根据每个类型,用工厂类调用。逐个完成。 没什么漂亮的代码,只有有效、稳定的代码。 代码中调用toJson toJson 代码 mapper.writeValueAsString ObjectMapper DefaultSerializerProvider 一堆实…...
