Einstein Summation 爱因斯坦求和 torch.einsum
Einstein Summation 爱因斯坦求和 torch.einsum
flyfish
理解爱因斯坦求和的基本概念和语法,这对初学者来说可能有一定难度。对于不熟悉该表示法的用户来说,可能不如直接的矩阵乘法表达式易于理解。
整个思路是
向量的点积 -》矩阵乘法-》einsum
向量之间的点积在几何上表示两个向量的投影和夹角,在代数上用于衡量向量的相似性,并且在物理学中用于计算力做的功。
矩阵乘法是由多个向量点积组成的,可以看作是多个向量点积的组合
einsum 操作可以用其他内置的矩阵运算函数来实现
使用 einsum 进行矩阵乘法
import torch# 定义两个矩阵
A = torch.randn(2, 3)
B = torch.randn(3, 4)# 使用 einsum 表示矩阵乘法
C = torch.einsum('ik,kj->ij', A, B)
print(C)
使用 matmul 进行矩阵乘法
import torch# 定义两个矩阵
A = torch.randn(2, 3)
B = torch.randn(3, 4)# 使用 matmul 表示矩阵乘法
C = torch.matmul(A, B)
print(C)
开始解释
向量之间的点积(也称为内积或标量积)在数学、物理学和计算中有着重要的意义。点积是两个向量乘积的一种特殊形式,其结果是一个标量。点积在许多领域中都有广泛的应用,包括向量的投影、计算角度、物理学中的功、机器学习中的相似性度量等。
点积的定义
给定两个n维向量 a \mathbf{a} a 和 b \mathbf{b} b,它们的点积定义如下:
a ⋅ b = ∑ i = 1 n a i b i \mathbf{a} \cdot \mathbf{b} = \sum_{i=1}^{n} a_i b_i a⋅b=∑i=1naibi
点积的几何意义
- 计算向量间的夹角:
点积可以用来计算两个向量之间的夹角 θ \theta θ。根据点积的定义,可以得到:
a ⋅ b = ∥ a ∥ ∥ b ∥ cos ( θ ) \mathbf{a} \cdot \mathbf{b} = \|\mathbf{a}\| \|\mathbf{b}\| \cos(\theta) a⋅b=∥a∥∥b∥cos(θ)
其中 ∥ a ∥ \|\mathbf{a}\| ∥a∥ 和 ∥ b ∥ \|\mathbf{b}\| ∥b∥ 分别是向量 a \mathbf{a} a 和 b \mathbf{b} b 的模(或长度)。因此,可以通过点积计算两个向量之间的夹角:
cos ( θ ) = a ⋅ b ∥ a ∥ ∥ b ∥ \cos(\theta) = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{a}\| \|\mathbf{b}\|} cos(θ)=∥a∥∥b∥a⋅b - 投影:
点积可以用来计算一个向量在另一个向量方向上的投影。例如,向量 a \mathbf{a} a 在向量 b \mathbf{b} b 方向上的投影长度为:
proj b a = a ⋅ b ∥ b ∥ \text{proj}_{\mathbf{b}} \mathbf{a} = \frac{\mathbf{a} \cdot \mathbf{b}}{\|\mathbf{b}\|} projba=∥b∥a⋅b
点积的代数意义
- 向量相似性:
在机器学习和数据分析中,点积可以用来衡量两个向量之间的相似性。如果两个向量的方向相同,它们的点积为正;如果两个向量的方向相反,它们的点积为负;如果两个向量正交,它们的点积为零。 - 功的计算:
在物理学中,点积用于计算力和位移的乘积,即功。例如,如果一个物体在力 F \mathbf{F} F 的作用下移动了位移 d \mathbf{d} d,则做的功为:
W = F ⋅ d W = \mathbf{F} \cdot \mathbf{d} W=F⋅d
例子
计算两个二维向量的点积
假设 a = [ a 1 , a 2 ] \mathbf{a} = [a_1, a_2] a=[a1,a2] 和 b = [ b 1 , b 2 ] \mathbf{b} = [b_1, b_2] b=[b1,b2],它们的点积为:
a ⋅ b = a 1 b 1 + a 2 b 2 \mathbf{a} \cdot \mathbf{b} = a_1 b_1 + a_2 b_2 a⋅b=a1b1+a2b2
import numpy as np# 定义两个向量
a = np.array([1, 2])
b = np.array([3, 4])# 计算点积
dot_product = np.dot(a, b)
print(dot_product) # 输出: 11
计算两个三维向量的夹角
假设 a = [ a 1 , a 2 , a 3 ] \mathbf{a} = [a_1, a_2, a_3] a=[a1,a2,a3] 和 b = [ b 1 , b 2 , b 3 ] \mathbf{b} = [b_1, b_2, b_3] b=[b1,b2,b3],它们的点积和夹角计算如下:
import numpy as np# 定义两个向量
a = np.array([1, 0, 0])
b = np.array([0, 1, 0])# 计算点积
dot_product = np.dot(a, b)# 计算向量的模
norm_a = np.linalg.norm(a)
norm_b = np.linalg.norm(b)# 计算夹角的余弦值
cos_theta = dot_product / (norm_a * norm_b)
theta = np.arccos(cos_theta)print(f"夹角: {np.degrees(theta)} 度") # 输出: 90.0 度
矩阵乘法
矩阵乘法是两个矩阵 A A A 和 B B B 的乘积 C C C,其中:
- 矩阵 A A A 的形状为 m × n m \times n m×n
- 矩阵 B B B 的形状为 n × p n \times p n×p
- 矩阵 C C C 的形状为 m × p m \times p m×p
矩阵乘法的定义是:
C i j = ∑ k = 1 n A i k B k j C_{ij} = \sum_{k=1}^{n} A_{ik} B_{kj} Cij=∑k=1nAikBkj
换句话说,矩阵 C C C 的元素 C i j C_{ij} Cij 是矩阵 A A A 的第 i i i 行和矩阵 B B B 的第 j j j 列的点积。
从矩阵乘法到向量点积
考虑两个矩阵 A A A 和 B B B,我们可以将矩阵乘法分解为一系列的向量点积:
- 提取行向量和列向量:
- 矩阵 A A A 的第 i i i 行可以表示为向量 a i \mathbf{a_i} ai。
- 矩阵 B B B 的第 j j j 列可以表示为向量 b j \mathbf{b_j} bj。
- 计算点积:
- C i j C_{ij} Cij 是向量 a i \mathbf{a_i} ai 和向量 b j \mathbf{b_j} bj 的点积,即:
C i j = a i ⋅ b j C_{ij} = \mathbf{a_i} \cdot \mathbf{b_j} Cij=ai⋅bj
例如,考虑矩阵 A A A 和 B B B:
A = ( 1 2 3 4 ) A =\begin{pmatrix}1 & 2 \\ 3 & 4 \\ \end{pmatrix} A=(1324)
B = ( 5 6 7 8 ) B = \begin{pmatrix} 5 & 6 \\ 7 & 8 \\ \end{pmatrix} B=(5768)
它们的乘积 C = A B C = AB C=AB 为:
C = ( 1 ⋅ 5 + 2 ⋅ 7 1 ⋅ 6 + 2 ⋅ 8 3 ⋅ 5 + 4 ⋅ 7 3 ⋅ 6 + 4 ⋅ 8 ) = ( 19 22 43 50 ) C = \begin{pmatrix} 1 \cdot 5 + 2 \cdot 7 & 1 \cdot 6 + 2 \cdot 8 \\ 3 \cdot 5 + 4 \cdot 7 & 3 \cdot 6 + 4 \cdot 8 \\ \end{pmatrix} = \begin{pmatrix} 19 & 22 \\ 43 & 50 \\ \end{pmatrix} C=(1⋅5+2⋅73⋅5+4⋅71⋅6+2⋅83⋅6+4⋅8)=(19432250)
在这里:
C 11 = 1 ⋅ 5 + 2 ⋅ 7 = 19 C 12 = 1 ⋅ 6 + 2 ⋅ 8 = 22 C 21 = 3 ⋅ 5 + 4 ⋅ 7 = 43 C 22 = 3 ⋅ 6 + 4 ⋅ 8 = 50 C_{11} = 1 \cdot 5 + 2 \cdot 7 = 19 \\ C_{12} = 1 \cdot 6 + 2 \cdot 8 = 22 \\ C_{21} = 3 \cdot 5 + 4 \cdot 7 = 43 \\ C_{22} = 3 \cdot 6 + 4 \cdot 8 = 50 C11=1⋅5+2⋅7=19C12=1⋅6+2⋅8=22C21=3⋅5+4⋅7=43C22=3⋅6+4⋅8=50
使用 PyTorch 进行矩阵乘法和点积
以下是如何在 PyTorch 中实现矩阵乘法和向量点积:
import torch
# 定义两个矩阵
A = torch.tensor([[1, 2], [3, 4]])
B = torch.tensor([[5, 6], [7, 8]])
# 使用 torch.matmul 进行矩阵乘法
C = torch.matmul(A, B)
print(C)
# 输出:
# tensor([[19, 22],
# [43, 50]])
# 提取行向量和列向量
a1 = A[0, :] # A 的第一行
b1 = B[:, 0] # B 的第一列
# 计算点积
dot_product = torch.dot(a1, b1)
print(dot_product)
# 输出: tensor(19)
爱因斯坦求和
爱因斯坦求和约定(Einstein Summation Convention)是一种在物理学和数学中简化张量运算表示的方法。它由阿尔伯特·爱因斯坦在他的广义相对论论文中引入。这个约定的核心思想是通过省略求和符号(∑),简化公式的书写,增强表达的简洁性和可读性。
背景与起源
在物理学中,尤其是在处理广义相对论和量子力学中的张量时,常常需要进行大量的求和运算。为了简化这些计算的书写,爱因斯坦提出了一种简便的表示法:对于任何重复出现的指标,默认对其进行求和。
具体规则
- 求和隐含性:在一个表达式中,如果一个指标(下标或上标)在一个单项式中出现两次,则认为对该指标求和。例如: a i b i = ∑ i a i b i a_i b_i = \sum_{i} a_i b_i aibi=∑iaibi在这种表示法中,i 被称为“哑指标”或“虚指标”。
- 自由指标:如果一个指标在表达式中仅出现一次,则称其为自由指标,这个指标代表一个范围的所有可能值。例如: c i = a i j b j c_i = a_{ij} b_j ci=aijbj这里的 i 是自由指标,而 j 是哑指标。
- 多重求和:可以在一个表达式中使用多个哑指标进行多重求和。例如: d = a i j b j k c k d = a_{ij} b_{jk} c_k d=aijbjkck在这个例子中,j 和 k 都是哑指标,意味着: d = ∑ j ∑ k a i j b j k c k d = \sum_{j} \sum_{k} a_{ij} b_{jk} c_k d=∑j∑kaijbjkck
在使用 torch.einsum 时,我们可以利用爱因斯坦求和约定来简洁地表示矩阵乘法、张量收缩等操作:
import torch# 矩阵乘法
A = torch.randn(3, 4)
B = torch.randn(4, 5)
C = torch.einsum('ik,kj->ij', A, B)
在上面的例子中,‘ik,kj->ij’ 表示矩阵乘法,其中 k k k 是求和下标,最终结果的维度由 i i i 和 j j j 确定。
‘ik,kj->ij’ 是爱因斯坦求和约定在 torch.einsum 中的一个具体应用,表示矩阵乘法。让我们详细解析一下这个表示:
表达式解析
- 输入张量:
- 假设我们有两个矩阵 A 和 B。
- A 的形状为 (i, k),即 A 有 i 行和 k 列。
- B 的形状为 (k, j),即 B 有 k 行和 j 列。
- 爱因斯坦求和约定:
- ‘ik,kj->ij’ 中的 ik 和 kj 分别对应输入张量 A 和 B 的维度标签。
- 中间的 , 用于分隔多个输入张量的维度标签。
- 箭头 -> 左侧表示输入张量的维度标签,右侧表示输出张量的维度标签。
- ‘ik,kj’ 表示对两个输入张量 A 和 B 进行操作,其中 k 是求和下标。
- 求和与输出:
- 在 ‘ik,kj’ 中,k 是求和下标,表示我们要对 k 维度进行求和。
- i 和 j 出现在箭头 -> 右侧,表示输出张量的维度标签。
举例说明
假设我们有两个矩阵:
A = ( a 11 a 12 a 21 a 22 a 31 a 32 ) , B = ( b 11 b 12 b 13 b 21 b 22 b 23 ) A = \begin{pmatrix} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{pmatrix}, \quad B = \begin{pmatrix} b_{11} & b_{12} & b_{13} \\ b_{21} & b_{22} & b_{23} \end{pmatrix} A= a11a21a31a12a22a32 ,B=(b11b21b12b22b13b23)
其中:
- A A A 是一个 3 × 2 3 \times 2 3×2 的矩阵,对应维度标签 ‘ik’(即 i = 3 i = 3 i=3, k = 2 k = 2 k=2)。
- B B B 是一个 2 × 3 2 \times 3 2×3 的矩阵,对应维度标签 ‘kj’(即 k = 2 k = 2 k=2, j = 3 j = 3 j=3)。
使用 torch.einsum 表示矩阵乘法:
import torchA = torch.tensor([[a11, a12],[a21, a22],[a31, a32]])B = torch.tensor([[b11, b12, b13],[b21, b22, b23]])C = torch.einsum('ik,kj->ij', A, B)
矩阵乘法过程
‘ik,kj->ij’ 表示通过对 k 维度进行求和,得到输出矩阵 C:
C = A ⋅ B C = A \cdot B C=A⋅B
其中:
C i j = ∑ k A i k B k j C_{ij} = \sum_{k} A_{ik} B_{kj} Cij=∑kAikBkj
即:
C i j = A i 1 B 1 j + A i 2 B 2 j C_{ij} = A_{i1}B_{1j} + A_{i2}B_{2j} Cij=Ai1B1j+Ai2B2j
结果
根据上面的定义,最终的结果 C 是一个 3 × 3 3 \times 3 3×3 的矩阵:
C = ( c 11 c 12 c 13 c 21 c 22 c 23 c 31 c 32 c 33 ) C = \begin{pmatrix} c_{11} & c_{12} & c_{13} \\ c_{21} & c_{22} & c_{23} \\ c_{31} & c_{32} & c_{33} \end{pmatrix} C= c11c21c31c12c22c32c13c23c33
每个元素 c i j c_{ij} cij 由对应的矩阵乘法和求和计算得到。
注意力机制
在编写注意力的时候有这样的代码
scores = torch.einsum(“blhe,bshe->bhls”, queries, keys)
从向量内积的角度解释
假设 queries 和 keys 的形状分别为 ( B , L , H , E ) (B, L, H, E) (B,L,H,E) 和 ( B , S , H , E ) (B, S, H, E) (B,S,H,E),其中:
- B B B 是批次大小 (Batch Size)
- L L L 是查询序列的长度 (Length of queries)
- S S S 是键序列的长度 (Length of keys)
- H H H 是注意力头的数量 (Number of heads)
- E E E 是嵌入维度 (Embedding Dimension)
我们计算 queries 和 keys 在嵌入维度 E E E 上的内积,即通过 torch.einsum(“blhe,bshe->bhls”, queries, keys) 来计算注意力得分。
示例
假设我们有以下输入:
import torchqueries = torch.tensor([[[[0.5, 1.2], [0.3, 0.7]], # 第一个 query 序列,两个头,每个头两个维度[[1.5, 2.2], [1.3, 1.7]], # 第二个 query 序列,两个头,每个头两个维度]
]) # 形状 (1, 2, 2, 2)keys = torch.tensor([[[[0.8, 1.5], [0.4, 0.9]], # 第一个 key 序列,两个头,每个头两个维度[[1.1, 2.3], [1.0, 1.5]], # 第二个 key 序列,两个头,每个头两个维度]
]) # 形状 (1, 2, 2, 2)
这里 queries 和 keys 的形状都是 (1, 2, 2, 2),表示 1 个批次,2 个序列,2 个头,每个头 2 个维度。
我们希望计算注意力得分矩阵 scores,其形状为 (1, 2, 2, 2)。
计算步骤
使用 torch.einsum 计算 scores:
scores = torch.einsum("blhe,bshe->bhls", queries, keys)
print(scores)
手动计算
头 1:
- 第一个 query 序列和第一个 key 序列的内积:
0.5 × 0.8 + 1.2 × 1.5 = 0.4 + 1.8 = 2.2 0.5 \times 0.8 + 1.2 \times 1.5 = 0.4 + 1.8 = 2.2 0.5×0.8+1.2×1.5=0.4+1.8=2.2 - 第一个 query 序列和第二个 key 序列的内积:
0.5 × 1.1 + 1.2 × 2.3 = 0.55 + 2.76 = 3.31 0.5 \times 1.1 + 1.2 \times 2.3 = 0.55 + 2.76 = 3.31 0.5×1.1+1.2×2.3=0.55+2.76=3.31 - 第二个 query 序列和第一个 key 序列的内积:
1.5 × 0.8 + 2.2 × 1.5 = 1.2 + 3.3 = 4.5 1.5 \times 0.8 + 2.2 \times 1.5 = 1.2 + 3.3 = 4.5 1.5×0.8+2.2×1.5=1.2+3.3=4.5 - 第二个 query 序列和第二个 key 序列的内积:
1.5 × 1.1 + 2.2 × 2.3 = 1.65 + 5.06 = 6.71 1.5 \times 1.1 + 2.2 \times 2.3 = 1.65 + 5.06 = 6.71 1.5×1.1+2.2×2.3=1.65+5.06=6.71
头 2:
- 第一个 query 序列和第一个 key 序列的内积:
0.3 × 0.4 + 0.7 × 0.9 = 0.12 + 0.63 = 0.75 0.3 \times 0.4 + 0.7 \times 0.9 = 0.12 + 0.63 = 0.75 0.3×0.4+0.7×0.9=0.12+0.63=0.75 - 第一个 query 序列和第二个 key 序列的内积:
0.3 × 1.0 + 0.7 × 1.5 = 0.3 + 1.05 = 1.35 0.3 \times 1.0 + 0.7 \times 1.5 = 0.3 + 1.05 = 1.35 0.3×1.0+0.7×1.5=0.3+1.05=1.35 - 第二个 query 序列和第一个 key 序列的内积:
1.3 × 0.4 + 1.7 × 0.9 = 0.52 + 1.53 = 2.05 1.3 \times 0.4 + 1.7 \times 0.9 = 0.52 + 1.53 = 2.05 1.3×0.4+1.7×0.9=0.52+1.53=2.05 - 第二个 query 序列和第二个 key 序列的内积:
1.3 × 1.0 + 1.7 × 1.5 = 1.3 + 2.55 = 3.85 1.3 \times 1.0 + 1.7 \times 1.5 = 1.3 + 2.55 = 3.85 1.3×1.0+1.7×1.5=1.3+2.55=3.85
最终结果
根据上述计算,我们可以得到:
scores = torch.tensor([[[[2.2, 3.31], [4.5, 6.71]], # 第一个头的得分[[0.75, 1.35], [2.05, 3.85]] # 第二个头的得分]
])
使用 PyTorch 计算
运行以下代码验证手动计算结果:
import torchqueries = torch.tensor([[[[0.5, 1.2], [0.3, 0.7]], [[1.5, 2.2], [1.3, 1.7]], ]
]) keys = torch.tensor([[[[0.8, 1.5], [0.4, 0.9]], [[1.1, 2.3], [1.0, 1.5]], ]
])scores = torch.einsum("blhe,bshe->bhls", queries, keys)
print(scores)
输出:
tensor([[[[2.2000, 3.3100],[4.5000, 6.7100]],[[0.7500, 1.3500],[2.0500, 3.8500]]]])
从矩阵乘法的角度解释
使用矩阵乘法计算
为了将 queries 和 keys 的计算表示成矩阵乘法,我们可以按以下步骤操作:
- 调整形状:
- 将 queries 和 keys 调整形状,使每个头的查询和键序列变成矩阵。
- 矩阵乘法:
- 对每个头分别进行矩阵乘法。
调整形状并进行矩阵乘法
我们将 queries 和 keys 形状从 (B, L, H, E) 和 (B, S, H, E) 调整为 (B, H, L, E) 和 (B, H, E, S),以便进行矩阵乘法。
queries_reshaped = queries.permute(0, 2, 1, 3) # (B, H, L, E)
keys_reshaped = keys.permute(0, 2, 3, 1) # (B, H, E, S)# 使用矩阵乘法
scores_matmul = torch.matmul(queries_reshaped, keys_reshaped) # (B, H, L, S)
print(scores_matmul)
输出:
tensor([[[[2.2000, 3.3100],[4.5000, 6.7100]],[[0.7500, 1.3500],[2.0500, 3.8500]]]])
这里的矩阵乘法使用 torch.matmul ,没有使用 torch.mm
torch.matmul 和 torch.mm 是 PyTorch 中用于矩阵乘法的两个函数,但它们在适用的张量维度上有一些不同。具体来说:
torch.mm
- 用途:专门用于两个二维矩阵(矩阵)之间的乘法。
- 输入:必须是两个二维张量,形状分别为 (m, n) 和 (n, p)。
- 输出:结果是一个二维张量,形状为 (m, p)。
示例:
import torch# 定义两个二维矩阵
A = torch.randn(2, 3)
B = torch.randn(3, 4)# 使用 torch.mm 进行矩阵乘法
C = torch.mm(A, B)
print(C.shape) # 输出: torch.Size([2, 4])
torch.matmul
- 用途:更通用的矩阵乘法函数,可以处理二维及以上的张量。
- 输入:可以是二维矩阵,也可以是具有更多维度的张量。
- 输出:根据输入张量的维度,输出可能是一个矩阵或更高维度的张量。
- 广播:torch.matmul 可以处理广播(broadcasting),即输入张量的形状可以不完全匹配,但需要满足广播规则。
示例:
import torch# 定义两个二维矩阵
A = torch.randn(2, 3)
B = torch.randn(3, 4)# 使用 torch.matmul 进行矩阵乘法
C = torch.matmul(A, B)
print(C.shape) # 输出: torch.Size([2, 4])# 定义两个三维张量
A_3d = torch.randn(5, 2, 3)
B_3d = torch.randn(5, 3, 4)# 使用 torch.matmul 进行三维张量的矩阵乘法
C_3d = torch.matmul(A_3d, B_3d)
print(C_3d.shape) # 输出: torch.Size([5, 2, 4])# 广播示例
A_broadcast = torch.randn(2, 3)
B_broadcast = torch.randn(5, 3, 4)# A_broadcast 的形状将广播成 (5, 2, 3)
C_broadcast = torch.matmul(A_broadcast, B_broadcast)
print(C_broadcast.shape) # 输出: torch.Size([5, 2, 4])
主要区别
- 适用维度:torch.mm 只适用于二维矩阵;torch.matmul 则适用于二维及以上维度的张量。
- 广播:torch.matmul 支持广播,而 torch.mm 不支持。
permute
在 PyTorch 中,permute 是一个张量(tensor)的方法,用于改变张量的维度顺序。这个操作不会改变张量的数据,只是重新排列它的维度。这对于需要改变数据的形状以适应不同操作的需求非常有用。
举例来说,如果你有一个形状为 (batch_size, height, width, channels) 的图像张量,而你的模型需要输入形状为 (batch_size, channels, height, width) 的张量,你可以使用 permute 方法来重新排列维度。
以下是一个简单的例子:
import torch# 创建一个形状为 (2, 3, 4, 5) 的随机张量
x = torch.randn(2, 3, 4, 5)# 使用 permute 方法改变维度顺序
x_permuted = x.permute(0, 3, 1, 2)# 打印新张量的形状
print(x_permuted.shape) # 输出: torch.Size([2, 5, 3, 4])
在这个例子中:
- 原始张量 x 的形状为 (2, 3, 4, 5)。
- 调用 x.permute(0, 3, 1, 2) 后,新张量 x_permuted 的形状变为 (2, 5, 3, 4)。
permute 方法的参数是新维度顺序的索引。例如,x.permute(0, 3, 1, 2) 意味着将第 0 维保持不变,将原第 3 维移到第 1 位置,将原第 1 维移到第 2 位置,将原第 2 维移到第 3 位置。
https://pytorch.org/docs/stable/generated/torch.transpose.html
https://pytorch.org/docs/stable/generated/torch.einsum.html
相关文章:

Einstein Summation 爱因斯坦求和 torch.einsum
Einstein Summation 爱因斯坦求和 torch.einsum flyfish 理解爱因斯坦求和的基本概念和语法,这对初学者来说可能有一定难度。对于不熟悉该表示法的用户来说,可能不如直接的矩阵乘法表达式易于理解。 整个思路是 向量的点积 -》矩阵乘法-》einsum 向…...

TCP攻击是怎么实现的,如何防御?
TCP(Transmission Control Protocol)是互联网协议族中的重要组成部分,用于在不可靠的网络上提供可靠的数据传输服务。然而,TCP协议的一些特性也使其成为攻击者的目标,尤其是DDoS(Distributed Denial of Ser…...

Chrome DevTools开发者调试工具
Chrome DevTools 是一个功能强大的网页开发工具,集成在谷歌浏览器中,帮助开发者调试和优化网页应用。以下是详细的功能说明和使用技巧: 1. 打开 DevTools 快捷键:按下 F12 或 CtrlShiftI(Windows/Linux)或…...

产品创新管理:从模仿到引领,中国企业的创新之路
一、引言 在全球化竞争日益激烈的今天,科技创新已成为推动国家经济增长和社会进步的关键动力。中国自改革开放四十年来,在科技创新领域取得了举世瞩目的成就,从跟踪模仿到自主研发,再到自主创新、开放创新和协同创新并举…...

Android 日志实时输出
开发中如果只是单纯的应用开发,Android studio基本上可以满足,但是如果应用和系统联调那就得用logcat实时输出了,我这里都是总结的实用经验,没那么多花里胡哨 Android 日志实时输出 1、输出 android log //分步,进入s…...

JavaEE初阶---多线程编程(一.线程与进程)
目录 🤣一.线程与进程的概念与联系: 进程的基本概念: 线程的基本概念: 进程和线程的区别与联系: 🙃代码执行实列: 1.通过继承Thread父类来实现多线程 2.通过实现Runnable接口来实现多线程…...

react+vite创建
要在本地初始化一个结合了React和Vite的项目,你可以遵循以下步骤: 1、安装Node.js: 确保你的机器上已安装了Node.js。如果未安装,请前往Node.js官网下载并安装。 2、使用终端或命令提示符: 打开你的终端(…...
)
软考 系统架构设计师系列知识点之杂项集萃(29)
接前一篇文章:软考 系统架构设计师系列知识点之杂项集萃(28) 第46题 以下描述中,( )不是嵌入式操作系统的特点。 A. 面向应用,可以进行裁剪和移植 B. 用于特定领域,不需要支持多任…...
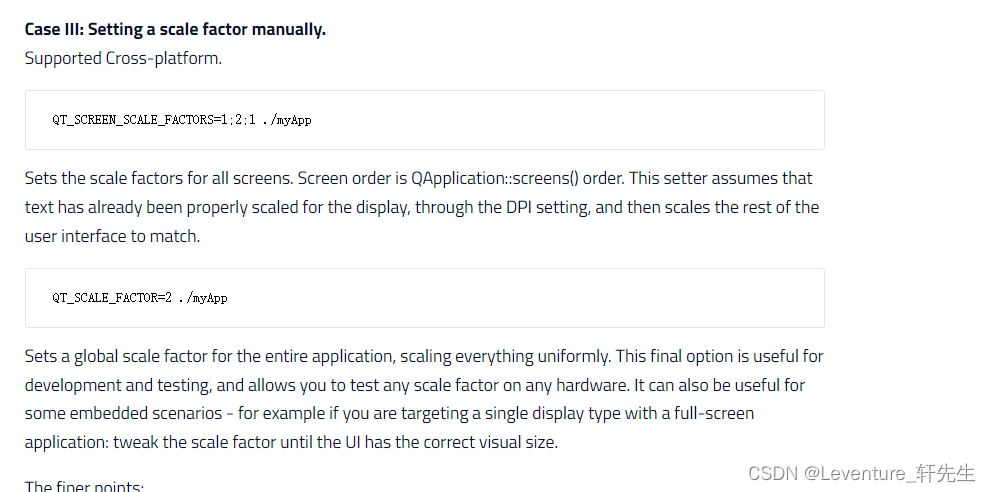
[Qt开发]当我们在开发兼容高分辨率和高缩放比、高DPI屏幕的软件时,我们在谈论什么。
前言 最近在开发有关高分辨率屏幕的软件,还是做了不少尝试的,当然我们也去网上查了不少资料,但是网上的资料也很零碎,说不明白,这样的话我就做个简单的总结,希望看到这的你可以一次解决你有关不同分辨率下…...

uniapp视频组件层级太高,解决方法使用subNvue原生子体窗口
目录 前言 先看一下uniapp官网的原话: subNvue的一些参数介绍 subNvues使用方法: 绑定id 显示 subNvue 弹出层 subNvue.show() 参数信息 subNvue.hide() 参数信息 在使用subNvue 原生子体窗口 遇到的一些问题 前言 nvue 兼容性 以及使用方式 控…...

java项目使用jsch下载ftp文件
pom <dependency><groupId>com.jcraft</groupId><artifactId>jsch</artifactId><version>0.1.55</version> </dependency>demo1:main方法直接下载 package com.example.controller;import com.jcraft.jsch.*; im…...
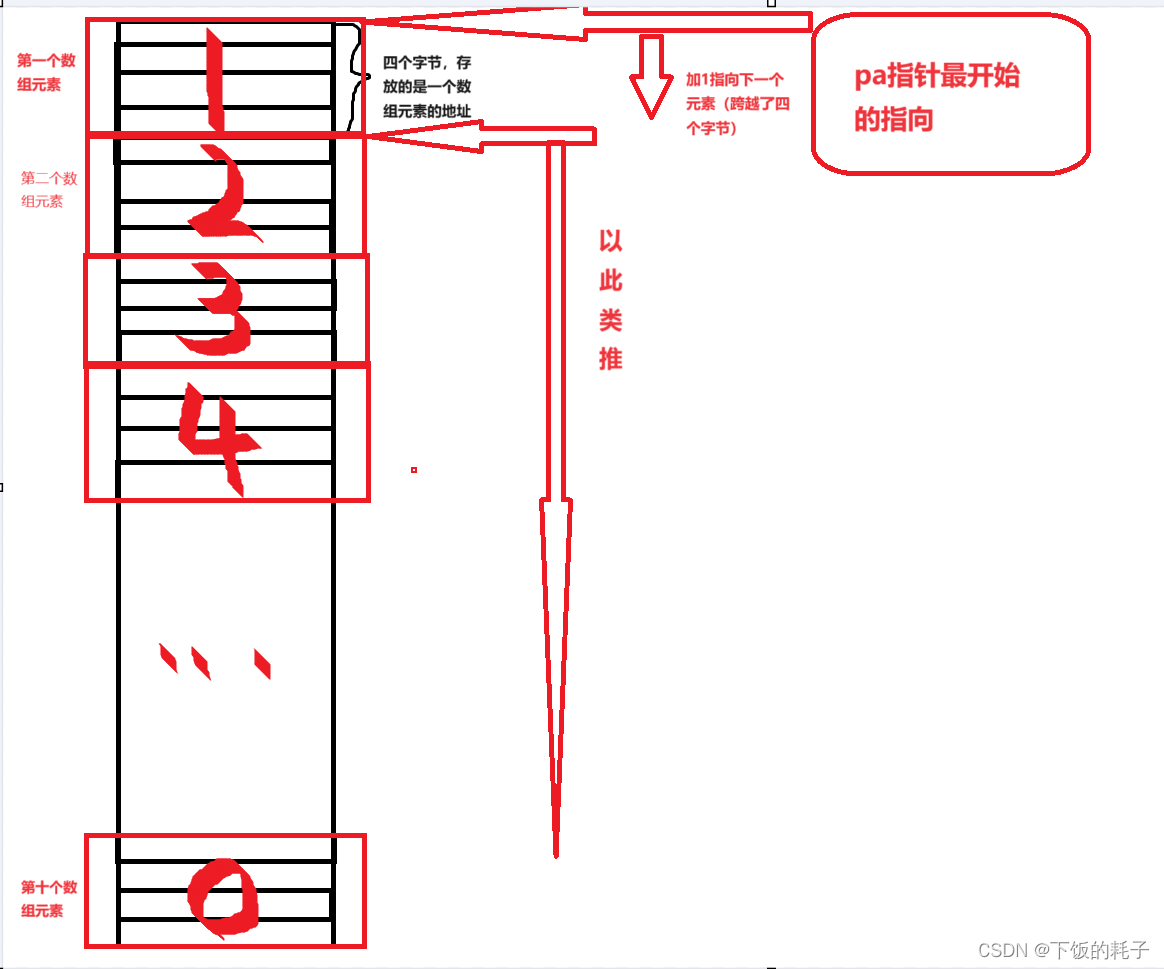
指针(初阶1)
一.指针是什么 通俗的讲,指针就是地址,其存在的意义就像宾馆房间的序号一样是为了更好的管理空间。 如下图: 如上图所示,指针就是指向内存中的一块空间,也就相当于地址 二.一个指针的大小是多少 之前我们学习过&#x…...

MySQL实体类框架
实现mysql数据库的增删改查功能 import com.mchange.v2.collection.MapEntry; import lombok.Data; import org.junit.jupiter.api.Test;import java.io.File; import java.io.FileOutputStream; import java.io.IOException; import java.lang.reflect.*; import java.sql.*; …...
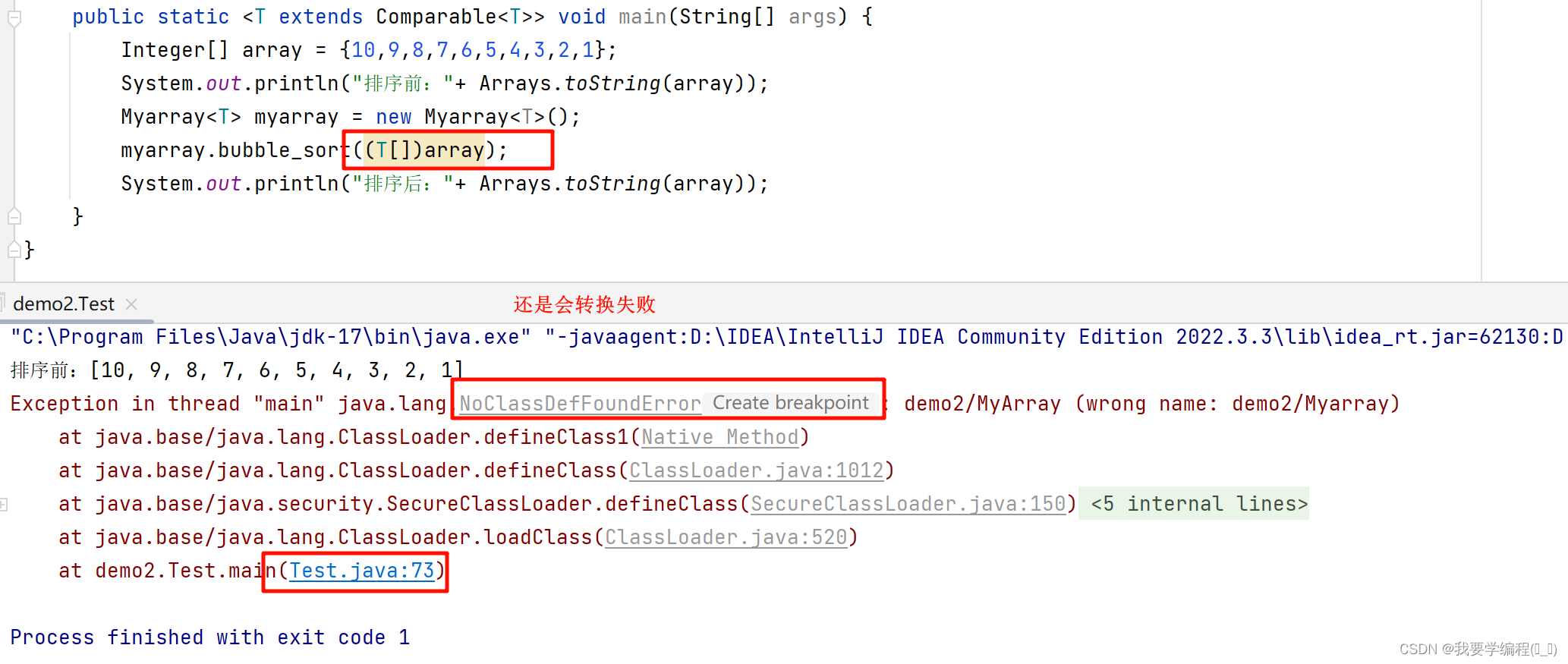
数据结构之初始泛型
找往期文章包括但不限于本期文章中不懂的知识点: 个人主页:我要学编程(ಥ_ಥ)-CSDN博客 所属专栏:数据结构(Java版) 目录 深入了解包装类 包装类的由来 装箱与拆箱 面试题 泛型 泛型的语法与使用…...

【网络编程开发】7.TCP可靠传输的原理
7.TCP可靠传输的原理 TCP实现可靠传输的原理主要基于序列号和确认应答、超时重传、滑动窗口、连接管理机制以及拥塞控制等多重机制。 TCP(Transmission Control Protocol),即传输控制协议,是网络通信中的一种重要协议࿰…...

视觉SLAM十四讲:从理论到实践(Chapter8:视觉里程计2)
前言 学习笔记,仅供学习,不做商用,如有侵权,联系我删除即可 一、目标 1.理解光流法跟踪特征点的原理。 2.理解直接法是如何估计相机位姿的。 3.实现多层直接法的计算。 特征点法存在缺陷: 二、光流(Optical Flow) …...

C语言过度C++语法补充(面向对象之前语法)
目录 1. C相较于C语言新增的语法 0. C 中的输入输出 1. 命名空间 1. 我们如何定义一个命名空间? 2. 如何使用一个命名空间 3. 命名空间中可以定义什么? 4. 在 相同或者不同 的文件中如果出现 同名的命名空间 会如何? 5. 总结~~撒花~~…...

类和对象(二)(C++)
初始化列表 class Date{public:Date(int year, int month, int day){_year year;_month month;_day day;}private:int _year;int _month;int _day;}; 虽然上述构造函数调用之后,对象中已经有了一个初始值,但是不能将其称为对对象中成员变量的初始化…...
Chrome DevTools解密:成为前端调试大师的终极攻略
Chrome DevTools是一套内置于Google Chrome浏览器中的开发者工具,它允许开发者对网页进行调试、分析和优化。本文将全面介绍DevTools的功能、使用方法以及注意事项,帮助开发者更好地利用这些工具来提升开发效率和网页性能。 一、简介 1. DevTools是什么…...

【python】OpenCV—Cartoonify and Portray
参考来自 使用PythonOpenCV将照片变成卡通照片 文章目录 1 卡通化codecv2.medianBlurcv2.adaptiveThresholdcv2.kmeanscv2.bilateralFilter 2 肖像画cv2.divide 1 卡通化 code import cv2 import numpy as npdef edge_mask(img, line_size, blur_value):gray cv2.cvtColor(…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

视频行为标注工具BehaviLabel(源码+使用介绍+Windows.Exe版本)
前言: 最近在做行为检测相关的模型,用的是时空图卷积网络(STGCN),但原有kinetic-400数据集数据质量较低,需要进行细粒度的标注,同时粗略搜了下已有开源工具基本都集中于图像分割这块,…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

【Kafka】Kafka从入门到实战:构建高吞吐量分布式消息系统
Kafka从入门到实战:构建高吞吐量分布式消息系统 一、Kafka概述 Apache Kafka是一个分布式流处理平台,最初由LinkedIn开发,后成为Apache顶级项目。它被设计用于高吞吐量、低延迟的消息处理,能够处理来自多个生产者的海量数据,并将这些数据实时传递给消费者。 Kafka核心特…...
