毫米波雷达阵列天线设计综合1(MATLAB仿真)
1 天线设计目标
毫米波雷达探测目标的距离、速度和角度,其中距离和角度和天线设计相关性较强。天线增益越高,则根据雷达方程可知探测距离越远;天线波束越窄,则角度分辨率越高;天线副瓣/旁瓣越低,则干扰越少,虚假目标越少。
天线的性能直接影响雷达性能,现代的毫米波雷达几乎都使用阵列天线。阵列天线是根据电磁波在空间相互干涉的原理,把具有相同结构、相同尺寸的基本天线单元按照一定规律排列在一起组成的。
综合来看,毫米波雷达使用阵列天线的目标是获得增益高、波束窄、旁瓣低的空间方向图,比较理想的天线辐射方向图如下图1-1所示,而图1-2所示的方向图则比较一般,因为出现较高的旁瓣和栅瓣。
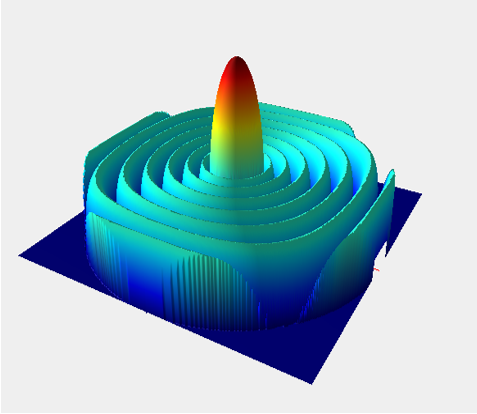
图1-1 理想方向图
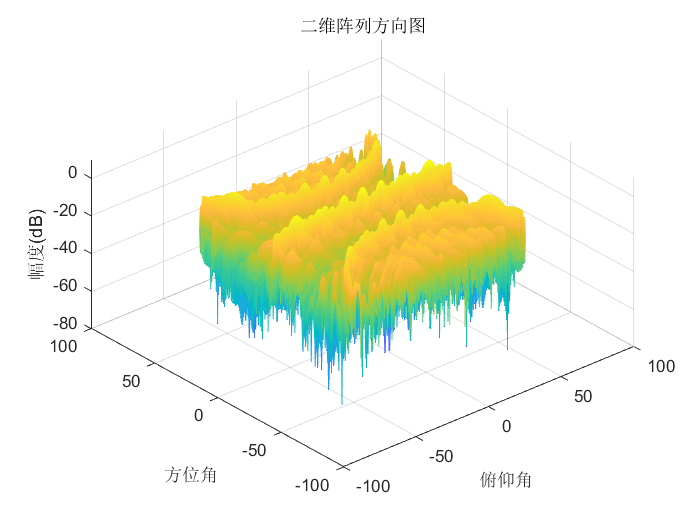
图1-2 一般的方向图
因此,阵列天线设计的目标是通过空间布局、激励幅度、激励相位的优化设计,获得理想的辐射特性,包括阵列天线方向图、半功率波束宽度、增益和效率、旁瓣电平等。
2 均匀间距阵列
阵列天线最容易想到的就是均匀排布,比如均匀直线排布、均匀平面排布等。空间上均匀排布的阵列天线旁瓣较高,可以通过调整每个阵元的激励幅度来获得低旁瓣。经典的激励幅度(馈电)分布有二项式分布、高斯分布、切比雪夫分布和泰勒分布等。
2.1 均匀间距直线阵列
32阵元均匀间距直线阵列使用不同的馈电分布的结果如下,资料可以参考《阵列天线理论与工程应用》。
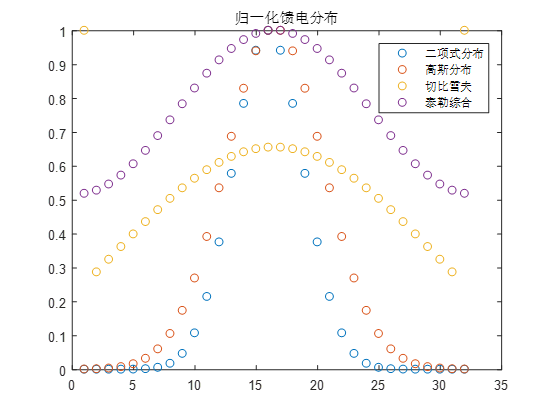
图2-1 不同的馈电分布
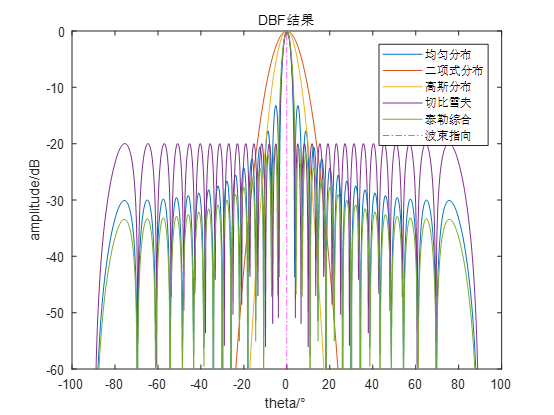
图2-2 不同馈电分布的接收波束形成
图2-1和2-2是32阵元等间距排布,但激励幅度(馈电)分布不同的仿真结果,可以看到,相比馈电均匀分布的情况,图2-1中的四种馈电分布形成的波束旁瓣均有明显的降低。
图2-1中二项式分布和高斯分布部分阵元馈电幅度较小,不适合实际使用;另外,图2-2中二项式分布和高斯分布的主瓣波束展宽较多,亦不适合实际使用,综上,切比雪夫和泰勒综合是较优的激励幅度优化方法,但只适用于均匀阵列。
2.2 均匀间距平面阵列
平面阵列也可以通过阵元的幅度控制,获得更好的增益和旁瓣水平。除了均匀分布馈电,这里使用了高斯分布、切比雪夫分布和泰勒分布等。下面使用24×24的二维平面阵列天线进行仿真,给出不同馈电的分布和不同馈电分布下的波束形成结果。
2.2.1 不同馈电分布仿真结果
这里使用MATLAB仿真了均匀分布、高斯分布、切比雪夫分布和泰勒分布的馈电结果,格子的大小和颜色代表了强度,每张图的右侧是相应的尺度。
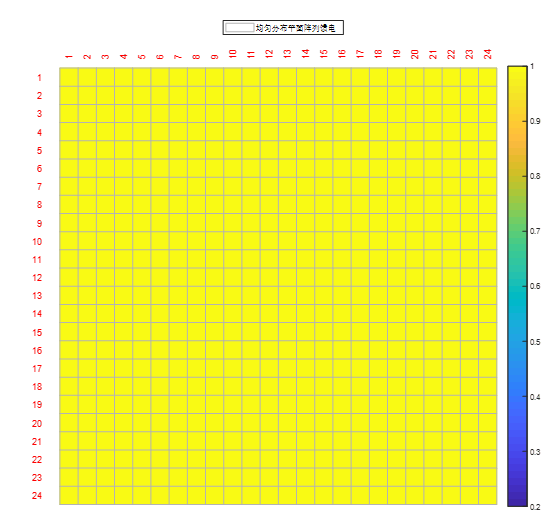
图2-3 均匀分布平面阵列馈电
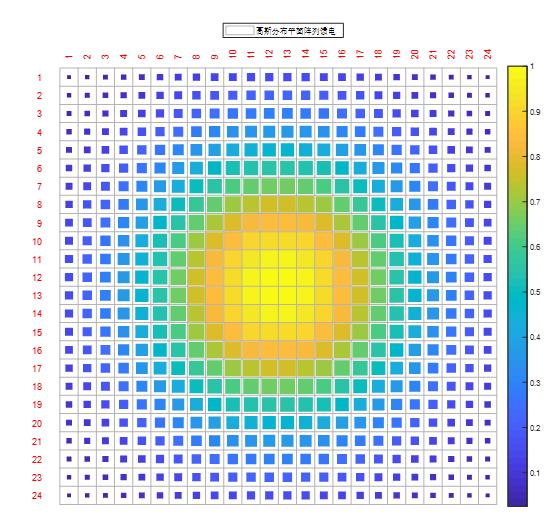
图2-4 高斯分布平面阵列馈电
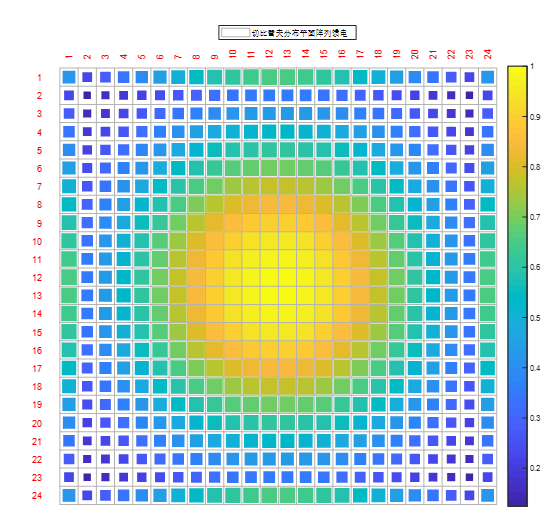
图2-5 切比雪夫分布平面阵列馈电
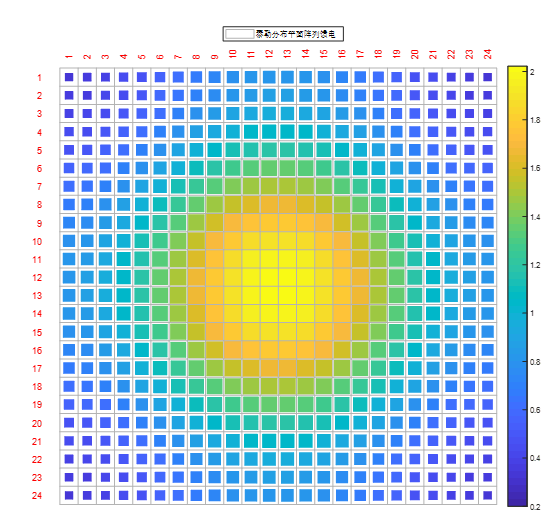
图2-6 泰勒分布平面阵列馈电
2.2.2 不同馈电分布方向图
不同馈电分布的平面阵列天线三维空间波束和俯视图的MATLAB仿真结果如下,可以看到相比于均匀分布,高斯分布、切比雪夫分布、泰勒分布的主瓣波束均有不同程度展宽,旁瓣也有明显降低。
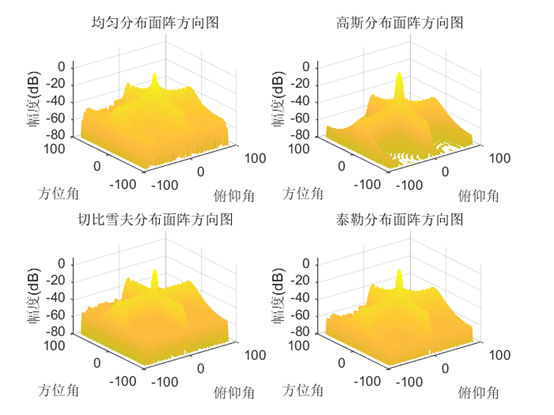
图2-7 不同馈电分布的平面阵列波束方向图
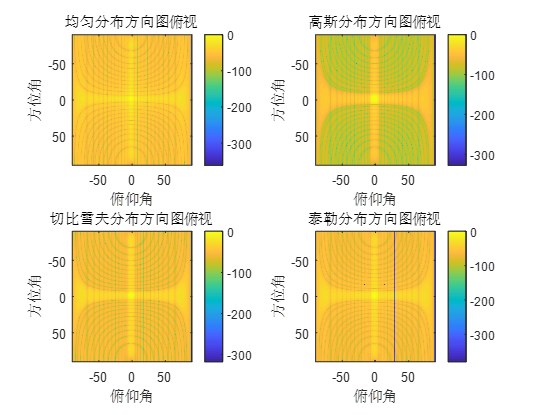
图2-8 不同馈电分布的平面阵列波束方向图俯视图
2.2.3 不同馈电分布主瓣和旁瓣
在方位和俯仰0°方向做切面,可以得到俯仰面和方位面的方向图,MATLAB仿真结果如下,可以看到,图2-9和图2-10中,高斯分布、切比雪夫分布和泰勒分布的旁瓣均明显降低,同时主瓣略有展宽。
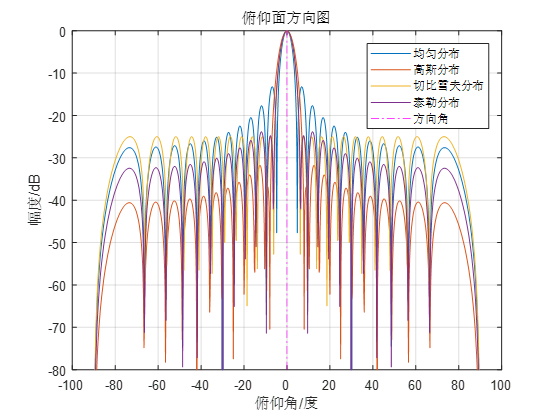
图2-9 不同馈电分布的俯仰切面方向图
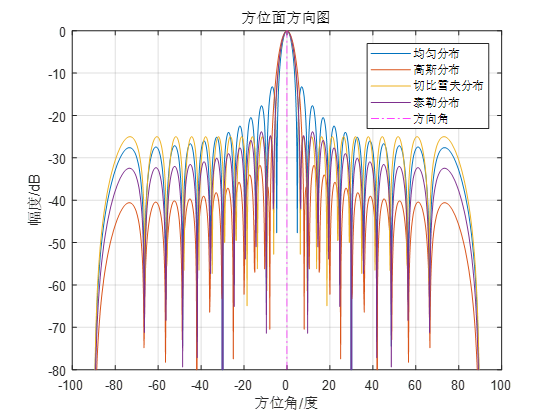
图2-10 不同馈电分布的方位切面方向图
3 非均匀间距阵列
实际的毫米波雷达通常使用非等间距的稀疏阵列天线,这样可以显著降低硬件成本,同时对毫米波雷达探测性能的影响很小。
特斯拉的4D雷达天线如下图所示,发射和接收使用了不同的疏状天线,如果把疏状天线看成一个子阵,方向图函数为![]() ,那么二维平面阵列的方向图可以看作N个子阵方向图的叠加:
,那么二维平面阵列的方向图可以看作N个子阵方向图的叠加:
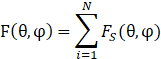
在接收时,可以对所有通道的数据做幅相加权合成不同的接收波束,则上式可以写为
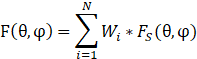
其中,![]() 是不同通道的幅相加权系数。
是不同通道的幅相加权系数。

图3-1 特斯拉4D雷达天线
每个子阵中,疏状天线的方向图由M个阵元的方向图叠加得到,可以用公式表示如下
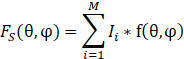
其中![]() 是单个阵元的方向图,
是单个阵元的方向图,![]() 是不同阵元的激励,设计不同的激励可以得到不同的方向图,如下图3-2和图3-3所示。
是不同阵元的激励,设计不同的激励可以得到不同的方向图,如下图3-2和图3-3所示。
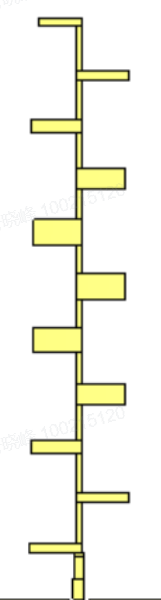
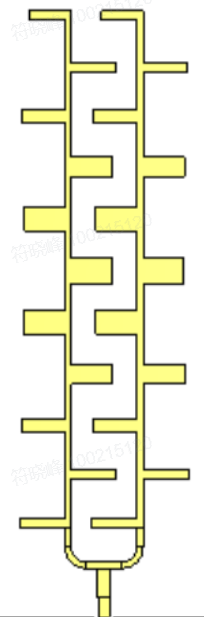
图3-2 典型疏状天线
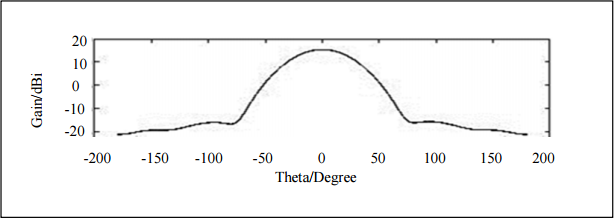
(a)E面方向图
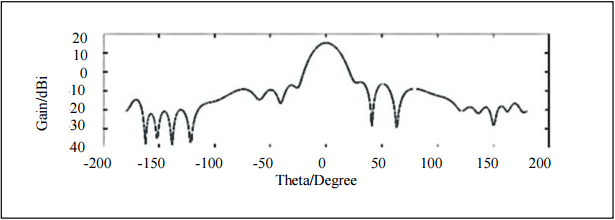
(b) H面方向图
图3-3 疏状天线方向图
阵列天线的布局和激励强度分布对方向图、旁瓣等均有较大影响,解析式的方法已经不适用,可以考虑智能搜索算法进行优化,比如遗传算法、模拟退火算法、粒子群优化算法等,这些内容将在后续博文介绍。
4 参考代码
直线阵列的馈电分布和方向图仿真的MATLAB代码如下,平面阵列的仿真代码量较大,博文不作分享,如有需要可私信交流。
% 均匀线阵波束形成
% 使用不同的激励权重仿真
clear; clc; close all;% 构造阵列和信号
N = 32; % 线阵长度
array_uni = 0:1:N-1; % 同样孔径下的均匀阵列
theta = 0; % 目标角度
d = 0.5; % 阵列均匀间隔d
A_uni = exp(-1i*2*pi*d*sind(theta).*array_uni.'); % 导向矢量
x_uni = A_uni; % 无噪声
% snr = 20; % 信噪比
% x_uni = awgn(A_uni,snr); % 添加噪声% 构造不同馈电的分布
bino_distri = GetBinoDistri(N); % 二项式分布,需要保证N>1
sigma = 4;
gauss_distri = GetGaussDistri(N,sigma); % 高斯分布,需要保证N>1
psll = -20;
cheb_distri = chebwin(N,-psll)'; % N是阵列单元个数,psll即我们希望的副瓣电平
cheb_distri = cheb_distri/max(cheb_distri);
taylor_distri = taylorwin(N,2,psll)';
taylor_distri = taylor_distri/max(taylor_distri);figure;
plot(bino_distri,'o');hold on;
plot(gauss_distri,'o');hold on;
plot(cheb_distri,'o');hold on;
plot(taylor_distri,'o');hold on;
legend('二项式分布','高斯分布','切比雪夫','泰勒综合');
title('归一化馈电分布');% 使用dbf扫描
thetascan = linspace(-90,90,1024);
a_uni = exp(1i*2*pi*d*sind(thetascan).'*array_uni);
p_uni = x_uni.'*a_uni.';
p_uni = 20*log10(abs(p_uni)./max(abs(p_uni)));
% 实际波束指向角度和理论偏差,这里不太关注
% [max_value,index] = max(p_uni);
% theta_est = thetascan(index);
% est_error = abs(theta_est - theta);
% 二项式分布
p_uni_bino = bino_distri.*x_uni.'*a_uni.';
p_uni_bino = 20*log10(abs(p_uni_bino)./max(abs(p_uni_bino)));
% 高斯分布
p_uni_gauss = gauss_distri.*x_uni.'*a_uni.';
p_uni_gauss = 20*log10(abs(p_uni_gauss)./max(abs(p_uni_gauss)));
% 高斯分布
p_uni_cheb = cheb_distri.*x_uni.'*a_uni.';
p_uni_cheb = 20*log10(abs(p_uni_cheb)./max(abs(p_uni_cheb)));
% 高斯分布
p_uni_taylor = taylor_distri.*x_uni.'*a_uni.';
p_uni_taylor = 20*log10(abs(p_uni_taylor)./max(abs(p_uni_taylor)));figure;
plot(thetascan,p_uni);hold on;
plot(thetascan,p_uni_bino);hold on;
plot(thetascan,p_uni_gauss);hold on;
plot(thetascan,p_uni_cheb);hold on;
plot(thetascan,p_uni_taylor);hold on;
plot([theta,theta],ylim,'m-.');
legend('均匀分布','二项式分布','高斯分布','切比雪夫','泰勒综合','波束指向');
ylim([-60,0]);
xlabel('theta/°');ylabel('amplitude/dB');
title('DBF结果');
% title(['DBF结果 SNR = ' num2str(snr)]);% 计算二项式分布幅度
function bino_distri = GetBinoDistri(N)bino_distri = zeros(1,N);for k = 1:1:Nbino_distri(k) = factorial(N)/(factorial(k)*factorial(N-k)); % 根据公式计算endbino_distri = bino_distri/max(bino_distri); % 归一化
end% 计算二项式分布幅度
function gauss_distri = GetGaussDistri(N,sigma)gauss_distri = zeros(1,N);u = (1+N)/2;const1 = 1/(sigma*sqrt(2*pi));const2 = (2*sigma^2);for k = 1:1:Ngauss_distri(k) = const1*exp(-(k-u)^2/const2); % 根据公式计算endgauss_distri = gauss_distri/max(gauss_distri); % 归一化
end相关文章:

毫米波雷达阵列天线设计综合1(MATLAB仿真)
1 天线设计目标 毫米波雷达探测目标的距离、速度和角度,其中距离和角度和天线设计相关性较强。天线增益越高,则根据雷达方程可知探测距离越远;天线波束越窄,则角度分辨率越高;天线副瓣/旁瓣越低,则干扰越少…...

Freemarker
Freemarker简介 Freemarker是一个用Java语言编写的模板引擎,用于基于模板和数据生成文本输出。它可以用于生成HTML网页、XML文档、电子邮件、配置文件等任何格式的文本。Freemarker将业务逻辑与表示逻辑分离,使得开发人员可以专注于功能实现,…...

基于Zero-shot实现LLM信息抽取
基于Zero-shot方式实现LLM信息抽取 在当今这个信息爆炸的时代,从海量的文本数据中高效地抽取关键信息显得尤为重要。随着自然语言处理(NLP)技术的不断进步,信息抽取任务也迎来了新的突破。近年来,基于Zero-shot&#x…...
【python】tkinter GUI编程经典用法,Label标签组件应用实战详解
✨✨ 欢迎大家来到景天科技苑✨✨ 🎈🎈 养成好习惯,先赞后看哦~🎈🎈 🏆 作者简介:景天科技苑 🏆《头衔》:大厂架构师,华为云开发者社区专家博主,…...
国产操作系统上给麒麟虚拟机安装virtualbox增强工具 _ 统信 _ 麒麟 _ 中科方德
原文链接:国产操作系统上给麒麟虚拟机安装virtualbox增强工具 | 统信 | 麒麟 | 中科方德 Hello,大家好啊!昨天给大家带来了一篇在国产操作系统上给VirtualBox中的Win7虚拟机安装增强工具的文章,今天我们将继续深入,介绍…...
 Object Pascal 学习笔记---第14章泛型第3节(特定类约束))
(delphi11最新学习资料) Object Pascal 学习笔记---第14章泛型第3节(特定类约束)
14.3.2 特定类约束 如果您的泛型类需要使用某个特定子集的类(特定层次结构),则可能需要根据给定基类指定约束。 例如,如果您声明: typeTCompClass<T: TComponent> class 则此泛型类的实例仅适用于组…...

【postgresql初级使用】视图上的触发器instead of,替代计划的rewrite,实现不一样的审计日志
instead of 触发器 专栏内容: postgresql使用入门基础手写数据库toadb并发编程 个人主页:我的主页 管理社区:开源数据库 座右铭:天行健,君子以自强不息;地势坤,君子以厚德载物. 文章目录 inst…...
定时器)
window.setInterval(func,interval)定时器
window.setInterval()是JavaScript中的方法,用于在指定的时间间隔重复执行某个函数或代码块。它接受两个参数,第一个参数是要执行的函数或代码块,第二个参数是时间间隔(以毫秒为单位)。 以下是使用window.setInterval…...

Einstein Summation 爱因斯坦求和 torch.einsum
Einstein Summation 爱因斯坦求和 torch.einsum flyfish 理解爱因斯坦求和的基本概念和语法,这对初学者来说可能有一定难度。对于不熟悉该表示法的用户来说,可能不如直接的矩阵乘法表达式易于理解。 整个思路是 向量的点积 -》矩阵乘法-》einsum 向…...

TCP攻击是怎么实现的,如何防御?
TCP(Transmission Control Protocol)是互联网协议族中的重要组成部分,用于在不可靠的网络上提供可靠的数据传输服务。然而,TCP协议的一些特性也使其成为攻击者的目标,尤其是DDoS(Distributed Denial of Ser…...

Chrome DevTools开发者调试工具
Chrome DevTools 是一个功能强大的网页开发工具,集成在谷歌浏览器中,帮助开发者调试和优化网页应用。以下是详细的功能说明和使用技巧: 1. 打开 DevTools 快捷键:按下 F12 或 CtrlShiftI(Windows/Linux)或…...

产品创新管理:从模仿到引领,中国企业的创新之路
一、引言 在全球化竞争日益激烈的今天,科技创新已成为推动国家经济增长和社会进步的关键动力。中国自改革开放四十年来,在科技创新领域取得了举世瞩目的成就,从跟踪模仿到自主研发,再到自主创新、开放创新和协同创新并举…...

Android 日志实时输出
开发中如果只是单纯的应用开发,Android studio基本上可以满足,但是如果应用和系统联调那就得用logcat实时输出了,我这里都是总结的实用经验,没那么多花里胡哨 Android 日志实时输出 1、输出 android log //分步,进入s…...

JavaEE初阶---多线程编程(一.线程与进程)
目录 🤣一.线程与进程的概念与联系: 进程的基本概念: 线程的基本概念: 进程和线程的区别与联系: 🙃代码执行实列: 1.通过继承Thread父类来实现多线程 2.通过实现Runnable接口来实现多线程…...

react+vite创建
要在本地初始化一个结合了React和Vite的项目,你可以遵循以下步骤: 1、安装Node.js: 确保你的机器上已安装了Node.js。如果未安装,请前往Node.js官网下载并安装。 2、使用终端或命令提示符: 打开你的终端(…...
)
软考 系统架构设计师系列知识点之杂项集萃(29)
接前一篇文章:软考 系统架构设计师系列知识点之杂项集萃(28) 第46题 以下描述中,( )不是嵌入式操作系统的特点。 A. 面向应用,可以进行裁剪和移植 B. 用于特定领域,不需要支持多任…...
[Qt开发]当我们在开发兼容高分辨率和高缩放比、高DPI屏幕的软件时,我们在谈论什么。
前言 最近在开发有关高分辨率屏幕的软件,还是做了不少尝试的,当然我们也去网上查了不少资料,但是网上的资料也很零碎,说不明白,这样的话我就做个简单的总结,希望看到这的你可以一次解决你有关不同分辨率下…...

uniapp视频组件层级太高,解决方法使用subNvue原生子体窗口
目录 前言 先看一下uniapp官网的原话: subNvue的一些参数介绍 subNvues使用方法: 绑定id 显示 subNvue 弹出层 subNvue.show() 参数信息 subNvue.hide() 参数信息 在使用subNvue 原生子体窗口 遇到的一些问题 前言 nvue 兼容性 以及使用方式 控…...

java项目使用jsch下载ftp文件
pom <dependency><groupId>com.jcraft</groupId><artifactId>jsch</artifactId><version>0.1.55</version> </dependency>demo1:main方法直接下载 package com.example.controller;import com.jcraft.jsch.*; im…...
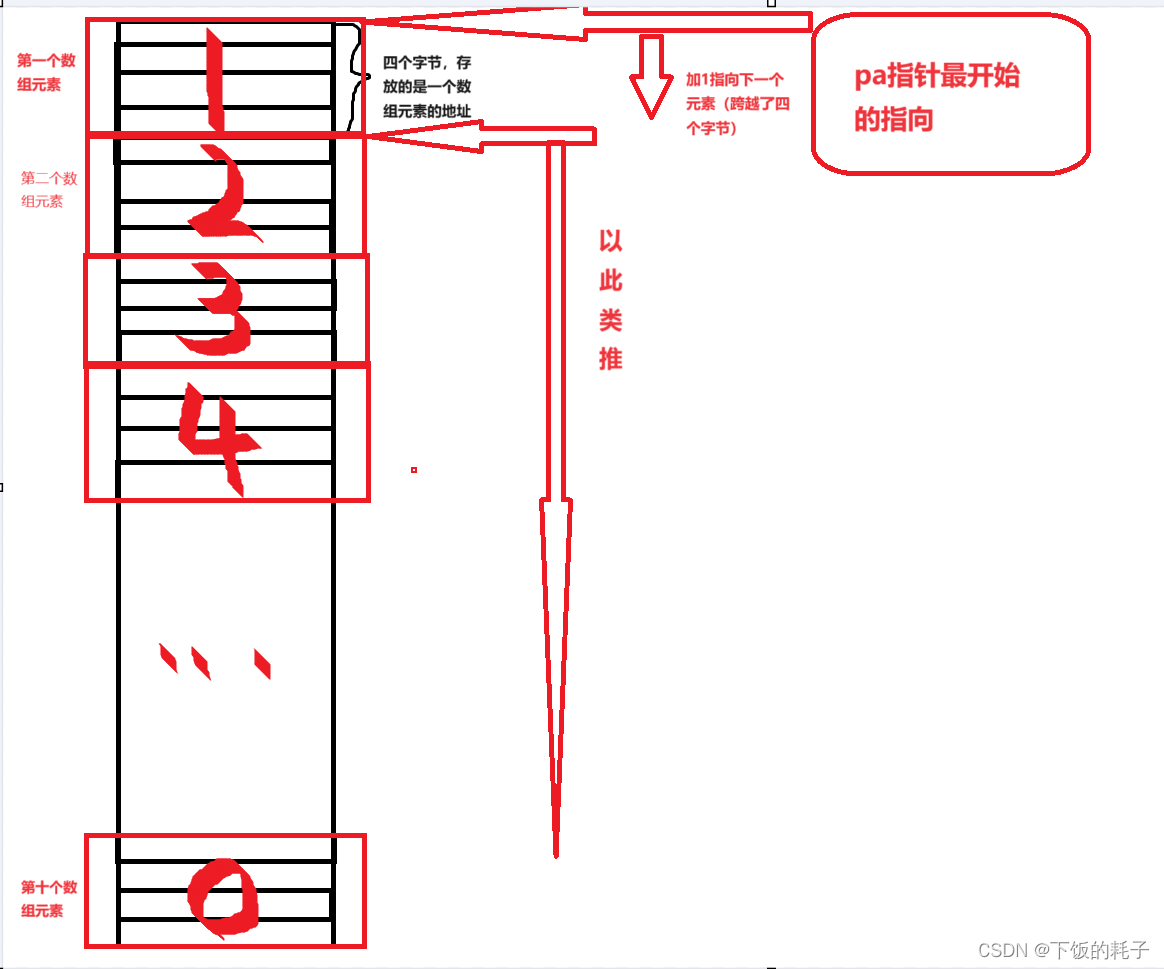
指针(初阶1)
一.指针是什么 通俗的讲,指针就是地址,其存在的意义就像宾馆房间的序号一样是为了更好的管理空间。 如下图: 如上图所示,指针就是指向内存中的一块空间,也就相当于地址 二.一个指针的大小是多少 之前我们学习过&#x…...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

【Nginx】使用 Nginx+Lua 实现基于 IP 的访问频率限制
使用 NginxLua 实现基于 IP 的访问频率限制 在高并发场景下,限制某个 IP 的访问频率是非常重要的,可以有效防止恶意攻击或错误配置导致的服务宕机。以下是一个详细的实现方案,使用 Nginx 和 Lua 脚本结合 Redis 来实现基于 IP 的访问频率限制…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

【C++】纯虚函数类外可以写实现吗?
1. 答案 先说答案,可以。 2.代码测试 .h头文件 #include <iostream> #include <string>// 抽象基类 class AbstractBase { public:AbstractBase() default;virtual ~AbstractBase() default; // 默认析构函数public:virtual int PureVirtualFunct…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...

软件工程 期末复习
瀑布模型:计划 螺旋模型:风险低 原型模型: 用户反馈 喷泉模型:代码复用 高内聚 低耦合:模块内部功能紧密 模块之间依赖程度小 高内聚:指的是一个模块内部的功能应该紧密相关。换句话说,一个模块应当只实现单一的功能…...

6️⃣Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙
Go 语言中的哈希、加密与序列化:通往区块链世界的钥匙 一、前言:离区块链还有多远? 区块链听起来可能遥不可及,似乎是只有密码学专家和资深工程师才能涉足的领域。但事实上,构建一个区块链的核心并不复杂,尤其当你已经掌握了一门系统编程语言,比如 Go。 要真正理解区…...
