2024年全国一高考数学压轴题

(3) 证明: 显然, 等差数列 { a 1 , . . . , a 4 n + 2 } \{a_{1},...,a_{4n+2}\} {a1,...,a4n+2} 是 ( i , j ) (i, j) (i,j)-可分的等价于等差数列 { 1 , . . . , 4 n + 2 } \{1,...,4n+2\} {1,...,4n+2} 是 ( i , j ) (i,j) (i,j)-可分的. 前推后显然, 我们考虑后推前, 在去掉第 i i i 和 j j j 项后, 若一个分割方案把 { 1 , . . . , 4 n + 2 } \{1,...,4n+2\} {1,...,4n+2} 分割成 n n n 个长为4的等差数列, 那么该分割方案也必然把 { a 1 , . . . , a 4 n + 2 } \{a_{1},...,a_{4n+2}\} {a1,...,a4n+2} 分割成 n n n 个长为4的等差数列, 因此二者等价.
考虑使得 { 1 , . . . , 4 n + 2 } \{1,...,4n+2\} {1,...,4n+2} ( i , j ) (i,j) (i,j)-可分的 ( i , j ) (i,j) (i,j) 的可行取值数目:
当 n = 1 n=1 n=1 时, 通过穷举, ( i , j ) (i,j) (i,j) 可取 ( 1 , 2 ) (1,2) (1,2), ( 1 , 6 ) (1,6) (1,6), ( 5 , 6 ) (5,6) (5,6). 当 n = k n=k n=k 时, 设 ( i , j ) (i,j) (i,j) 有 x k x_k xk 个可行取值, 考虑当 n = k + 1 n = k+1 n=k+1 时: { 1 , . . . , 4 k + 6 } \{1,...,4k+6\} {1,...,4k+6} 的前 4 4 4 项和后 4 k + 2 4k+2 4k+2 项分别构成两个等差数列. 由此易知, 将 n = k n=k n=k 时的每个 ( i , j ) (i,j) (i,j) 可行取值整体加 4 4 4, 就构成了当前的一个可行取值. 容易验证, 每个 i , j > 4 i,j>4 i,j>4 的可行取值都可以视为这么得到的. 接下来我们考虑 i < 4 i<4 i<4 的可行取值. 依然是枚举, 令 i i i 取 1 1 1, j j j 取 ( 1 , 4 s + 2 ) (1, 4s+2) (1,4s+2), 其中 0 ≤ s ≤ n 0\leq s \leq n 0≤s≤n, 此时 i i i, j j j 之间的数的个数为 4 4 4 的整数倍, j + 1 j+1 j+1 到 4 n + 2 4n+2 4n+2 之间数的个数为 4 4 4 的整数倍, 显然这个 ( i , j ) (i,j) (i,j) 的取值是可行的, 即 ( 1 , 4 s + 2 ) (1, 4s+2) (1,4s+2), 0 ≤ s ≤ n 0\leq s \leq n 0≤s≤n 是可行的. 设 2 ≤ d ≤ n 2\leq d\leq n 2≤d≤n, 则 1 1 1 到 4 d 4d 4d 刚好可以分成 d d d 个长度为4的等差数列 { 1 , . . . , 1 + 3 d } \{1,...,1+3d\} {1,...,1+3d}, { 2 , . . . , 2 + 3 d } \{2,...,2+3d\} {2,...,2+3d}, …, { d , . . . , 4 d } \{d,...,4d\} {d,...,4d}, 2 + 4 d 2+4d 2+4d 与 4 d 4d 4d 之间刚好隔了一个数 4 d + 1 4d+1 4d+1, 去除 2 2 2 和 4 d + 1 4d+1 4d+1, 1 1 1 到 4 d + 2 4d+2 4d+2 也可以分成 d d d 个长度为 4 4 4 的等差数列 { 1 , . . . , 1 + 3 d } \{1,...,1+3d\} {1,...,1+3d}, { 2 + d , . . . , 2 + 4 d } \{2+d,...,2+4d\} {2+d,...,2+4d}, …, { d , . . . , 4 d } \{d,...,4d\} {d,...,4d}. 令 i i i 取 2 2 2, j = 4 d + 1 j=4d+1 j=4d+1, 则去除 i i i 和 j j j 后 1 1 1 到 4 d + 2 4d+2 4d+2 也刚好可以分成 4 4 4 个长度为 4 4 4 的等差数列, 剩下的数相邻四个为一组可以分成长度为 4 4 4 的若干等差数列, 所以此时的 ( i , j ) (i,j) (i,j) 取值是可行的, 即 ( 2 , 4 d + 1 ) (2, 4d+1) (2,4d+1), 2 ≤ d ≤ n 2\leq d \leq n 2≤d≤n 是可行的. 因此 n = k + 1 n=k+1 n=k+1 时的可行取值数目至少为 x k + 1 = x k + 2 k + 2 x_{k+1}=x_k+2k+2 xk+1=xk+2k+2. 递推可得 x k + 1 ≥ 3 + 2 ( 1 + . . . + k ) + 2 k = k 2 + 3 k + 3 x_{k+1} \geq 3+2(1+...+k)+2k=k^2+3k+3 xk+1≥3+2(1+...+k)+2k=k2+3k+3.
综上, 尽管没求出可行取值的具体数目, 但可知其下界为 n 2 + n + 1 n^2+n+1 n2+n+1. 使得数列 { a 1 , . . . , a 4 m + 2 } \{a_1,...,a_{4m+2}\} {a1,...,a4m+2} ( i , j ) (i,j) (i,j)-可分的 ( i , j ) (i,j) (i,j) 可行取值数目至少为 m 2 + m + 1 m^2+m+1 m2+m+1. 所以随机抽取两个 1 1 1 到 4 m + 2 4m+2 4m+2 的数 ( i , j ) (i, j) (i,j), 其使得 { a 1 , . . . , a 4 m + 2 } \{a_1,...,a_{4m+2}\} {a1,...,a4m+2} ( i , j ) (i,j) (i,j)-可分的概率至少为:
m 2 + m + 1 ( 2 m + 1 ) ( 4 m + 1 ) = m 2 + m + 1 8 m 2 + 6 m + 1 > 1 8 \frac{m^2+m+1}{(2m+1)(4m+1)}=\frac{m^2+m+1}{8m^2+6m+1}\gt \frac{1}{8} (2m+1)(4m+1)m2+m+1=8m2+6m+1m2+m+1>81
PS: 不是数学专业的… 只是喜欢数学的工科生而已. 没做出来, 想到了用数学归纳法做, 但是令 i = 2 i=2 i=2的时候, 试出来 j = 5 j=5 j=5是不可行的, 13 + 12 n 13+12n 13+12n 是可行的, 所以认为是隔 12 12 12 一个, 没想到5只是一个特例而已, 实际上9之后就可以, 被误导了方向, 他如果第二问是让证 ( 2 , 9 ) (2,9) (2,9) 或许就做出来了. 本16届表示上学的时候压根没见过这样的题, 而且现在选修三选一怎么没了?
相关文章:

2024年全国一高考数学压轴题
(3) 证明: 显然, 等差数列 { a 1 , . . . , a 4 n 2 } \{a_{1},...,a_{4n2}\} {a1,...,a4n2} 是 ( i , j ) (i, j) (i,j)-可分的等价于等差数列 { 1 , . . . , 4 n 2 } \{1,...,4n2\} {1,...,4n2} 是 ( i , j ) (i,j) (i,j)-可分的. 前推后显然, 我们考虑后推前, 在去…...

springboot+vue前后端项目接口校验通信数据完整性
方案:使用国密SM3算法实现数字签名 服务端 maven的pom文件引用 <!-- 国密算法支持 --><dependency><groupId>org.bouncycastle</groupId><artifactId>bcprov-jdk15to18</artifactId><version>1.69</version><…...

进程通信(IPC-Inter Process Communication)
进程之间的通信通过内核空间实现 IPC技术 ①管道(匿名管道/命名管道-FIFO队列) ②System V IPC(消息队列、信号量和共享内存) ③套接字(UNIX套接字&Internet套接字) ※信号 软中断,信号提供了一种处理异步事件的方法,作为进程通信的一种机制&am…...
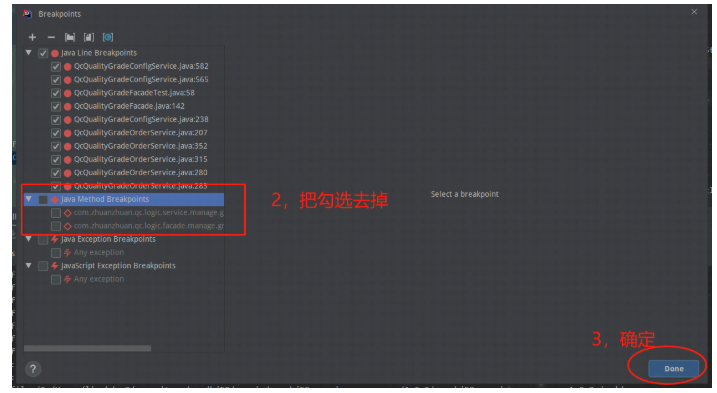
idea debug时提示”Method breakpoints may dramatically slow down debugging“的解决办法
问题现象 今天同事喊我过去看一个问题,项目正常启动的时候没问题,debug模式就卡住了,很久不动。我推测是哪个断点导致的,一看断点果然有情况。在方法上打了断点。 解决方式(Android Studio一样的解决) 1、View Brea…...
计算机缺失msvcp100.dll如何解决?教你5种简单高效的修复方法
在现代科技发展的时代,计算机已经成为我们生活和工作中不可或缺的工具。然而,在使用计算机的过程中,我们常常会遇到各种问题和困扰。其中之一就是计算机找不到msvcp100.dll文件。这个问题可能会给我们的生活和工作带来很多不便,下…...

对硬盘的设想2:纸存,硬指针,软指针
“纸存”是设想中的存储器,它只能改写两次:写一次,再改一次,然后就不能再动了。就像拿着钢笔在纸上写字一样,所以叫纸存。 硬指针P、软指针S S abcd S aPcdPx P aPcdPx S aycd ①一个软指针S,指向数据abcd…...

Python在股票交易分析中的应用:布林带与K线图的实战回测
引言 在股票交易的世界中,技术分析是投资者们用来预测市场动向的重要工具。布林带(Bollinger Bands)作为一种动态波动范围指标,因其直观性和实用性而广受欢迎。本文将通过Python代码,展示如何使用布林带结合K线图来分…...

现代密码学-认证、消息认证码
什么是单向散列函数 单向散列函数(one way hash function):一个输入:消息(message),一个固定长度的输出(散列值,hash value),根据散列值检查消息完整性(integrity) 单向散列函数也称为消息摘要…...

在Java中为什么对a赋值为10,在进行a++时还是等于10呢
首先我们看这样一组代码 public class demo1 {public static void main(String[] args) {int a10;aa;System.out.println(a);} } 结果:10不是在第二步有a操作吗?为什么还是10呢? a的执行步骤如下: 保存当前a的值(即10…...
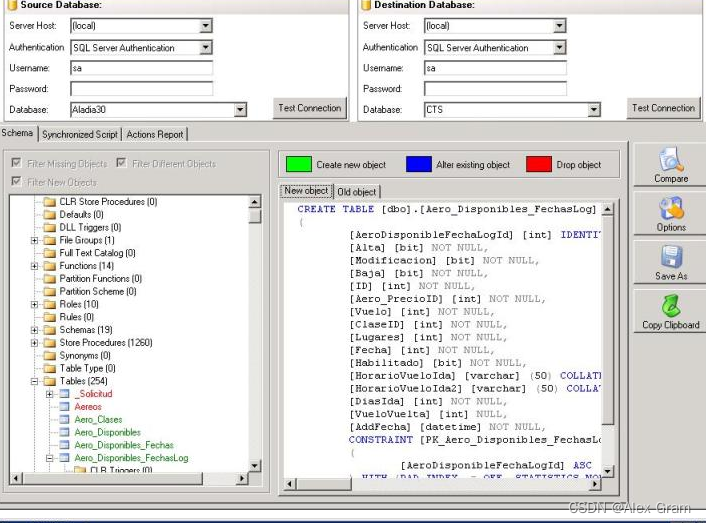
免费数据库同步软件
在信息化日益发展的今天,数据同步成为了企业和个人用户不可或缺的一部分。数据库同步软件作为数据同步的重要工具,能够帮助我们实现不同数据库系统之间的数据复制和同步,确保数据的一致性和完整性。本文将介绍几款免费数据库同步软件…...

如何轻松修改Windows远程连接的端口号
为了增强远程连接的安全性,最好修改默认的远程桌面协议(RDP)端口号。以下步骤将指导您如何修改Windows注册表中的端口设置,并相应地更新防火墙规则。 一、修改注册表中的端口号 打开注册表编辑器: 按下Win R键&#…...
)
Leetcode 54. 螺旋矩阵(二维数组移动坐标)
54. 螺旋矩阵 使用vis数组记录该位置是否已经被访问 定义一个int型dir来记录方向,0123分别代表右下左上 当越界或碰壁已访问的位置后,修改dir并计算下一个位置 否则根据原dir计算下一个位置 class Solution {public List<Integer> spiralOrder(i…...

深度图的方法实现加雾,Synscapes数据集以及D455相机拍摄为例
前言 在次之前,我们已经做了图像加雾的一些研究,这里我们将从深度图的方法实现加雾展开细讲 图像加雾算法的研究与应用_图像加雾 算法-CSDN博客 接下来将要介绍如何使用深度图像生成雾效图像的方法。利用Synscapes数据集,通过读取EXR格式的…...

QT: 读写ini配置文件(实现qml界面登录,修改)
目录 一.功能介绍 二.暴露属性 三.指定INI文件的路径和格式。 四.登录操作 1.检查INI文件中是否含有登录信息; 2.读取存储的ID; 3.读取存储的密码; 4.成功返回1;失败返回2; 五.修改账号 1.检查INI文件中是否含有登录信…...

DevOps 安全集成:从开发到部署,全生命周期安全守护
目录 一、DevOps 安全集成:为什么要做? 二、DevOps 安全集成:如何做? 三、DevOps 安全集成的优势 四、DevOps 安全集成:一些最佳实践 五、DevOps 安全集成:未来展望 六、思考与建议 七、总结 DevOps…...

R语言数据分析15-xgboost模型预测
XGBoost模型预测的主要大致思路: 1. 数据准备 首先,需要准备数据。这包括数据的读取、预处理和分割。数据应该包括特征和目标变量。 步骤: 读取数据:从CSV文件或其他数据源读取数据。数据清理:处理缺失值、异常值等…...
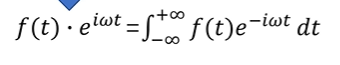
重构大学数学基础_week04_从点积理解傅里叶变换
这周我们来看一下傅里叶变换。傅里叶变换是一种在数学和许多科学领域中广泛应用的分析方法,它允许我们将信号或函数从其原始域(通常是时间域或空间域)转换到频域表示。在频域中,信号被表示为其组成频率的幅度和相位,这…...

Shell以及Shell编程
Shell的任务 ①分析命令; ②处理通配符、变量替换、命令替换、重定向、管道和作业控制; ③搜索命令并执行。 内部命令:内嵌在Shell中。 外部命令:存在于磁盘上的独立可执行文件。 #!/bin/bash #! 称为一个幻数&…...

从记忆到想象:探索AI的智能未来
引言 人工智能(AI)在信息处理、数据分析和任务自动化等方面展现了强大的能力。然而,在人类独有的记忆和想象力领域,AI仍然有很长的路要走。加利福尼亚大学戴维斯分校的心理学和神经科学教授查兰兰加纳特(Charan Ranga…...
“安全生产月”专题报道:AI智能监控技术如何助力安全生产
今年6月是第23个全国“安全生产月”,6月16日为全国“安全宣传咨询日”。今年全国“安全生产月”活动主题为“人人讲安全、个个会应急——畅通生命通道”。近日,国务院安委会办公室、应急管理部对开展好2024年全国“安全生产月”活动作出安排部署。 随着科…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...

苹果AI眼镜:从“工具”到“社交姿态”的范式革命——重新定义AI交互入口的未来机会
在2025年的AI硬件浪潮中,苹果AI眼镜(Apple Glasses)正在引发一场关于“人机交互形态”的深度思考。它并非简单地替代AirPods或Apple Watch,而是开辟了一个全新的、日常可接受的AI入口。其核心价值不在于功能的堆叠,而在于如何通过形态设计打破社交壁垒,成为用户“全天佩戴…...

Kafka主题运维全指南:从基础配置到故障处理
#作者:张桐瑞 文章目录 主题日常管理1. 修改主题分区。2. 修改主题级别参数。3. 变更副本数。4. 修改主题限速。5.主题分区迁移。6. 常见主题错误处理常见错误1:主题删除失败。常见错误2:__consumer_offsets占用太多的磁盘。 主题日常管理 …...

DBLP数据库是什么?
DBLP(Digital Bibliography & Library Project)Computer Science Bibliography是全球著名的计算机科学出版物的开放书目数据库。DBLP所收录的期刊和会议论文质量较高,数据库文献更新速度很快,很好地反映了国际计算机科学学术研…...

【51单片机】4. 模块化编程与LCD1602Debug
1. 什么是模块化编程 传统编程会将所有函数放在main.c中,如果使用的模块多,一个文件内会有很多代码,不利于组织和管理 模块化编程则是将各个模块的代码放在不同的.c文件里,在.h文件里提供外部可调用函数声明,其他.c文…...
