【位运算】【前缀和】个人练习-Leetcode-1177. Can Make Palindrome from Substring
题目链接:https://leetcode.cn/problems/can-make-palindrome-from-substring/description/
题目大意:给出一个字符串s,每次query给出l, r, k,要求判断子串s[l:r+1]在经过k次操作后是否能变为回文串。一次操作可以将子串内的一个字符变为任意一个其他字符。并且子串顺序可以任意改变。
思路:因为有很多query,自然想到会有重复计算,要检查超时,那么就想到前缀和。用pre[j][i]记录到i为止字母j出现的次数。那么子串内字母j出现的次数即为pre[j][r+1-l]。
对于子串,如果长度为奇数,那么回文与否与中间的字符无关,我们可以忽略。因此处理的总是一个总长度为偶数的子串。统计子串中每个字母的出现次数,可以知道,【奇数出现的次数】必然是偶数,因为只有偶数个奇数+若干偶数才能使得和(子串总长度)为偶数。
那么对于cnt个出现奇数次的字母,我们进行k次操作可以最多让2*k长度的子串变为回文。而对于出现偶数次的字母,只需将其对称排列即可。因此判断条件变为cnt / 2 <= k
完整代码
class Solution {
public:vector<bool> canMakePaliQueries(string s, vector<vector<int>>& queries) {int N = s.length();int pre[26][10001] = {};for (int i = 0; i < N; i++) {int idx = s[i]-'a';pre[idx][i+1] = pre[idx][i]+1;for (int j = 0; j < 26; j++) {if (j != idx && i > 0)pre[j][i+1] = pre[j][i];}}vector<bool> res;for (auto q: queries) {int l = q[0], r = q[1], k = q[2];char mid = s[(l+r)/2];bool flag = (r+1-l)%2;int arr[26] = {};if (flag)arr[mid-'a']--;int cnt = 0;for (int j = 0; j < 26; j++) {arr[j] += pre[j][r+1] - pre[j][l];if (arr[j] & 1 == 1) {cnt++;}}if (cnt / 2 <= k) {res.emplace_back(true);}else {res.emplace_back(false);}}return res;}
};
然而,碰到大的测试样例的时候会超时…那么就不得不求助高效的位运算了。
我们用一个二进制数组存储前缀和,每个二进制数一共26位,代表某个字母在i位置前的奇偶性。奇偶性运算用异或操作^来实现。
int N = s.length();vector<int> pre(N+1, 0);for (int i = 0; i < N; i++) {pre[i+1] = pre[i] ^ (1 << s[i]-'a'); }
如何统计子串中的字母的奇数的个数呢?这就是数一下【代表该区间的二进制数】(通过前缀和做差得到)中1的个数。
int l = q[0], r = q[1], k = q[2];int cnt = 0;int x = pre[r+1] ^ pre[l];while (x > 0) {x &= x - 1;cnt++;}
x &= x-1操作将 x 的二进制表示中最低位的 1 翻转成 0,并将所有更低位的位都清零。这是一个位运算技巧,快速计算二进制数中1的个数。
另外,由于乘法比除法更加快速,我们就不考虑是否忽略子串最中间的字母了,即使它使得x中1的个数增加了,也只不过增加1而已,我们将能够处理的上限改为2*k+1即可。
if (cnt <= 2*k+1)res.emplace_back(true);elseres.emplace_back(false);
完整代码
class Solution {
public:vector<bool> canMakePaliQueries(string s, vector<vector<int>>& queries) {int N = s.length();vector<int> pre(N+1, 0);for (int i = 0; i < N; i++) {pre[i+1] = pre[i] ^ (1 << s[i]-'a'); }vector<bool> res;for (auto q: queries) {int l = q[0], r = q[1], k = q[2];int cnt = 0;int x = pre[r+1] ^ pre[l];while (x > 0) {x &= x - 1;cnt++;}if (cnt <= 2*k+1)res.emplace_back(true);elseres.emplace_back(false);}return res;}
};
相关文章:

【位运算】【前缀和】个人练习-Leetcode-1177. Can Make Palindrome from Substring
题目链接:https://leetcode.cn/problems/can-make-palindrome-from-substring/description/ 题目大意:给出一个字符串s,每次query给出l, r, k,要求判断子串s[l:r1]在经过k次操作后是否能变为回文串。一次操作可以将子串内的一个字…...
最小相位系统
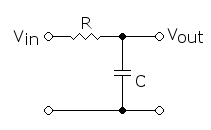
最小相位系统 1、传递函数 一个线性系统的响应。 比如一个RC低通滤波器: 交流分量在电容的充放电中被滤除掉,通过设置电容器的电容值,以及电阻值,能够控制这种滤除能力,这个参数为RC。 电容的电抗为 1 / j w C 1/j…...

css系列:进度条
前言 技术来源于需求,近期遇到了做语音的需求,有个调整语速和音量的进度条,UI组件库的进度条大部分不支持拖动和点击修改当前进度,所以自己手写了一个。 实现思路 MDN文档介绍 <input type"range"> - HTML&am…...

QT中为程序加入超级管理员权限
QT中为程序加入超级管理员权限 Chapter1 QT中为程序加入超级管理员权限1. mingw编译器2. MSVC编译器3. CMAKE Chapter2 如何给QT程序添加管理员权限(UAC)的几种方法1、Qt Creator中方案一:(仅适用于使用msvc编译器)方案二:&#x…...
)
共识算法之争(PBFT,Raft,PoW,PoS,DPoS)
文章目录 共识算法拜占庭容错技术(Byzantine Fault Tolerance,BFT)PBFT:Practical Byzantine Fault Tolerance,实用拜占庭容错算法Raft协议POW(Proof of Work)工作量证明机制POSDPoS(Delegated Proof of St…...

抽象的java入门1.3.0
前言: 在1.2.0版本中我们介绍了public class hello {}并从中提取出两个新概 修饰符和作用域 public class hello {public static void main(String[] args) {System.out.println("Hello World");} } 正片: 这一期把剩余的内容刨析出来 pub…...

【Oracle生产运维】表空间可用性告警排查处理
1 前言 在生产环境中,一般设置表空间告警阈值是90%,在接到监控报警后,并不是需要立刻对表空间进行扩容。 决定是否扩容主要看表空间最近的增量是多少,假如剩余10%的空间还能支持1个月的增量,那就不需要急着扩容。如果…...

mac Network: use --host to expose
本地启动无法访问,这个不是权限问题是mac 主机端口安全策略,现在我们只需要开启端口自动检测就可以 npm run dev --host 网络:未暴露 方案一 1、执行 npm run dev -- --host 方案二 1、请在 vite.config.js server: {host: true } 1…...

ChatGPT-4o体验demo
OpenAI 最近推出了其最新的人工智能语言模型——GPT-4O。该模型是在原有 GPT-4 的基础上进行优化而成,旨在提升生成质量和响应速度。GPT-4O 采用了更加高效的架构设计,使其在处理复杂文本时表现出更快的速度和更高的准确性。GPT-4O 在训练过程中融入了最…...
FPGA SPI采集ADC7606数据
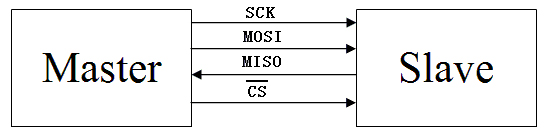
一,SPI总线的构成及信号类型 SPI总线只需四条线(如图1所示)就可以完成MCU与各种外围器件的通讯: 1)MOSI – Master数据输出,Slave数据输入 2)MISO – Master数据输入,Slave数据输出 3)SCK – 时钟信号,由Master产生 4)/CS – Slave使能信号,由Master控制。 在一个SPI时…...
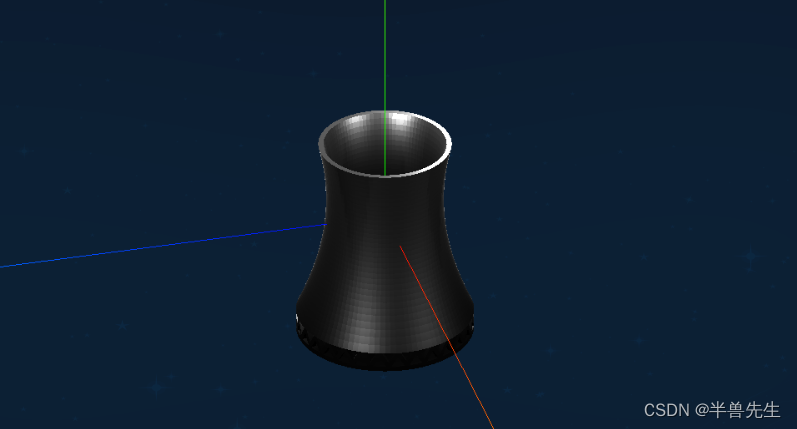
html three.js 引入.stl模型示例
1.新建一个模块用于放置模型 <div id"chart_map" style"width:800px;height:500px"></div> 2. 引入代码根据需求更改 <!-- 在head或body标签内加入以下链接 --> <script src"https://cdn.jsdelivr.net/npm/three0.137/build/t…...

从零手写实现 nginx-11-文件处理逻辑与 range 范围查询合并
前言 大家好,我是老马。很高兴遇到你。 我们为 java 开发者实现了 java 版本的 nginx https://github.com/houbb/nginx4j 如果你想知道 servlet 如何处理的,可以参考我的另一个项目: 手写从零实现简易版 tomcat minicat 手写 nginx 系列 …...

Java算法-力扣leetcode-167. 两数之和 II - 输入有序数组
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 ****非递减顺序排列 ** ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 < index1 < index2 < n…...

实战 | YOLOv10 自定义数据集训练实现车牌检测 (数据集+训练+预测 保姆级教程)
导读 本文主要介绍如何使用YOLOv10在自定义数据集训练实现车牌检测 (数据集训练预测 保姆级教程)。 YOLOv10简介 YOLOv10是清华大学研究人员在Ultralytics Python包的基础上,引入了一种新的实时目标检测方法,解决了YOLO以前版本在后处理和模型架构方面…...

自定义类型:结构体+结构体内存对齐+结构体实现位段
结构体内存对齐实现位段 一.结构体1.结构体的声明2.结构体变量成员访问操作符3.结构体传参4.匿名结构体5.结构的自引用 二.结构体内存对齐1.对齐规则2.为什么存在内存对齐?3.修改默认对齐数 三.结构体实现位段1.什么是位段2.位段的内存分配3.位段的跨平台问题4.位段…...
 command)
0109__strip(1) command
strip(1) command_linux strip-CSDN博客...

英码科技推出鸿蒙边缘计算盒子:提升国产化水平,增强AI应用效能,保障数据安全
当前,随着国产化替代趋势的加强,鸿蒙系统Harmony OS也日趋成熟和完善,各行各业都在积极拥抱鸿蒙;那么,边缘计算要加快实现全面国产化,基于鸿蒙系统开发AI应用势在必行。 关于鸿蒙系统及其优势 鸿蒙系统是华…...

从军事角度理解“战略与战术”
战略与战术,均源于军事术语。 战略(Strategy),源自希腊语词汇“strategos(将军)”和“strategia(军事指挥部,即将军的办公室和技能)”。指的是指挥全局性作战规划的谋略…...

最短路径——迪杰斯特拉与弗洛伊德算法
一.迪杰斯特拉算法 首先对于最短路径来说:从vi-vj的最短路径,不用非要经过所有的顶点,只需要找到路径最短的路径即可; 那么迪杰斯特拉的算法:其实也就与最小生成树的思想类似,找到较小的,然后…...
6.7.11 一种新的迁移学习方法可提高乳房 X 线摄影筛查中乳腺癌的诊断率
分割是一种将图像分割成离散区域的技术,以便将感兴趣的对象与周围环境分开。为了制定治疗计划,分割可以帮助医生测量乳房中的组织量。 二元分类问题的目的是将输入数据分为两组互斥的数据。在这种情况下,训练数据根据要解决的问题以二进制格…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

aardio 自动识别验证码输入
技术尝试 上周在发学习日志时有网友提议“在网页上识别验证码”,于是尝试整合图像识别与网页自动化技术,完成了这套模拟登录流程。核心思路是:截图验证码→OCR识别→自动填充表单→提交并验证结果。 代码在这里 import soImage; import we…...

TJCTF 2025
还以为是天津的。这个比较容易,虽然绕了点弯,可还是把CP AK了,不过我会的别人也会,还是没啥名次。记录一下吧。 Crypto bacon-bits with open(flag.txt) as f: flag f.read().strip() with open(text.txt) as t: text t.read…...

CTF show 数学不及格
拿到题目先查一下壳,看一下信息 发现是一个ELF文件,64位的 用IDA Pro 64 打开这个文件 然后点击F5进行伪代码转换 可以看到有五个if判断,第一个argc ! 5这个判断并没有起太大作用,主要是下面四个if判断 根据题目…...
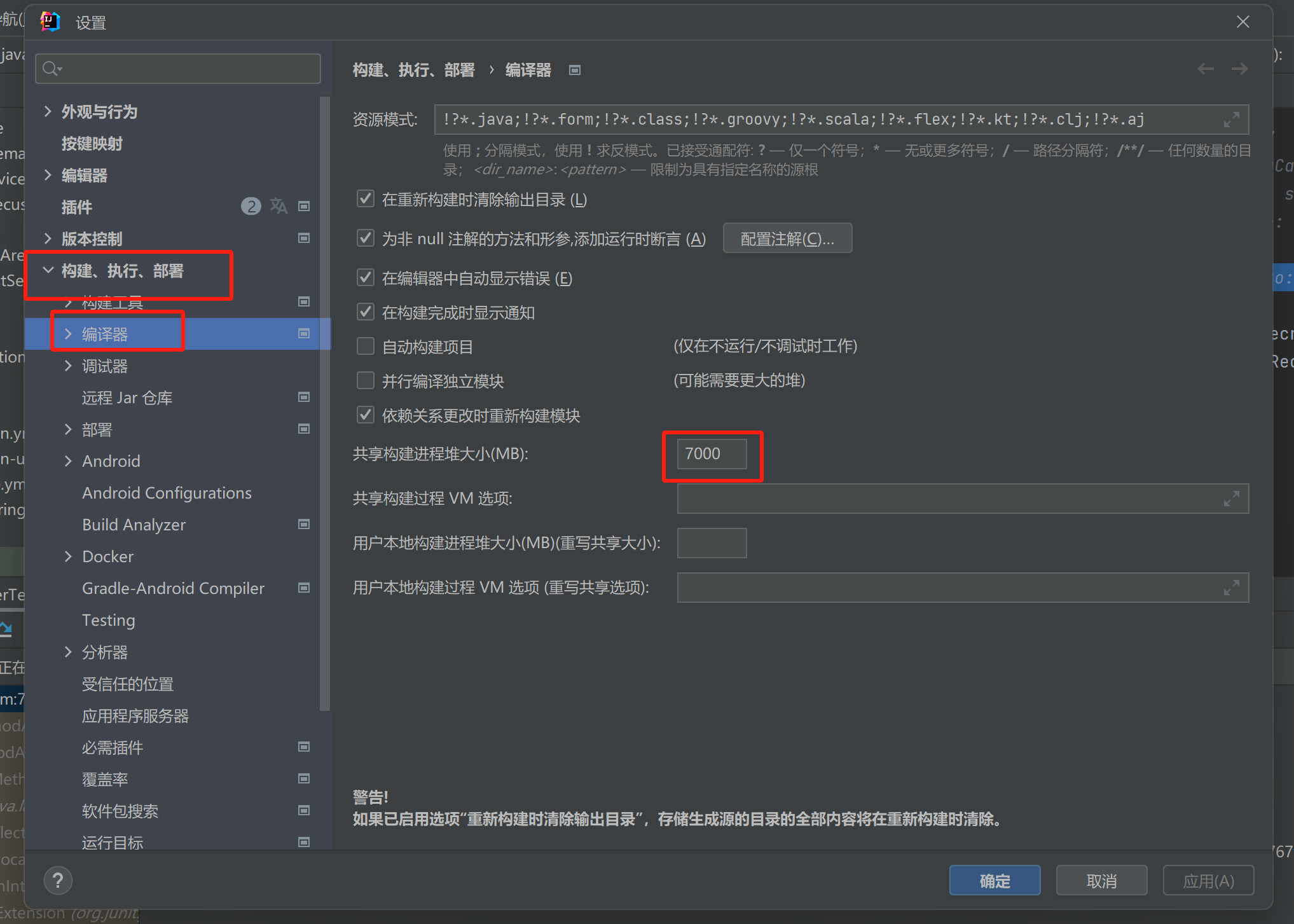
【记录坑点问题】IDEA运行:maven-resources-production:XX: OOM: Java heap space
问题:IDEA出现maven-resources-production:operation-service: java.lang.OutOfMemoryError: Java heap space 解决方案:将编译的堆内存增加一点 位置:设置setting-》构建菜单build-》编译器Complier...
