MATLAB——DFT(离散傅里叶变换)
题目1:
已知有限长序列x(n)为:
x(n)=[0,1,2,3,4,5,6,7,8,9],求x(n)的DFT和IDFT。要求
1)画出序列傅里叶变换对应的|X(k)|和arg[X(k)]图形。
2)画出原信号与傅里叶逆变换IDFT[X(k)]图形进行比较。
知识点:
DFT(Discrete Fourier Transform)和IDFT(Inverse Discrete Fourier Transform)是互为逆运算的变换。
给定一个长度为 NNN 的复数序列 x0,x1,x2,…,xN−1x_0, x_1, x_2, \dots, x_{N-1}x0,x1,x2,…,xN−1,DFT 将其转换为另一个长度为 NNN 的复数序列 X0,X1,X2,…,XN−1X_0, X_1, X_2, \dots, X_{N-1}X0,X1,X2,…,XN−1:
Xk=∑n=0N−1xne−j2πkn/N,k=0,1,2,…,N−1X_k=\sum_{n=0}^{N-1}x_n e^{-j2\pi kn/N}, \quad k=0,1,2,\dots,N-1Xk=n=0∑N−1xne−j2πkn/N,k=0,1,2,…,N−1
IDFT 则将 X0,X1,X2,…,XN−1X_0, X_1, X_2, \dots, X_{N-1}X0,X1,X2,…,XN−1 转换回 x0,x1,x2,…,xN−1x_0, x_1, x_2, \dots, x_{N-1}x0,x1,x2,…,xN−1:
xn=1N∑k=0N−1Xkej2πkn/N,n=0,1,2,…,N−1x_n=\frac{1}{N}\sum_{k=0}^{N-1}X_k e^{j2\pi kn/N}, \quad n=0,1,2,\dots,N-1xn=N1k=0∑N−1Xkej2πkn/N,n=0,1,2,…,N−1
程序:
主要是根据变换公式来的,不要忘了逆变换要除以N,有了前面 DFS的基础,这个代码相对比较简单。
xn=[0,1,2,3,4,5,6,7,8,9];
N=length(xn);
n=0:N-1;
k=0:N-1;
WN=exp(-2*j*pi/N);XK=xn*WN.^(n'*k);
x=XK*WN.^(-n'*k)/N;
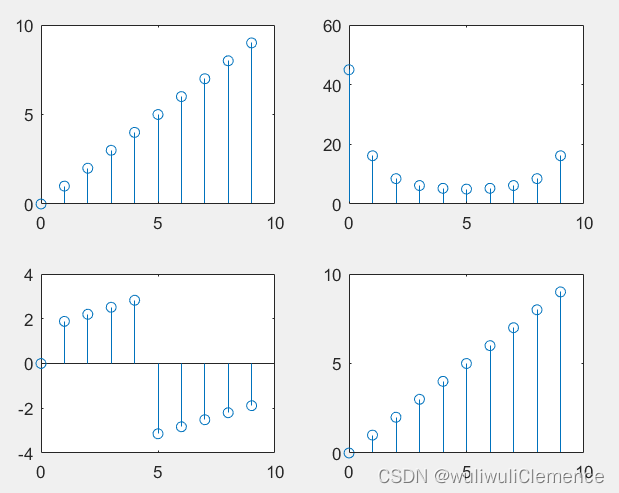
subplot(221);
stem(n,xn);
subplot(222);
stem(k,abs(XK));
subplot(223);
stem(k,angle(XK));
subplot(224);
stem(n,x);
运行结果:
题目2:
有限长序列DFT与周期序列DFS的联系
已知周期序列的主值x(n)=[0,1,2,3,4,5],求x(n)周期重复次数为4次时的DFS。要求
1)画出原主值序列和信号周期序列;
2)画出序列傅里叶变换对的图形。
知识点:
我们知道,在时域上。周期序列可以看做是有限长序列的周期延拓。在频域上是否也这样呢。答案是肯定的,现在来进行验证。
代码:
x0=[0,1,2,3,4,5];
N0=length(x0);
n0=0:N0-1;
k0=0:N0-1;
x1=x0';%转置
xn=x1*ones(1,4);
xn=xn(:)';
NN=length(xn);
nn=0:NN-1;
kn=0:NN-1;
%nn=0:4*N0-1;
%kn=0:4*N0-1;
%xn=x0(mod(nn,N0)+1);
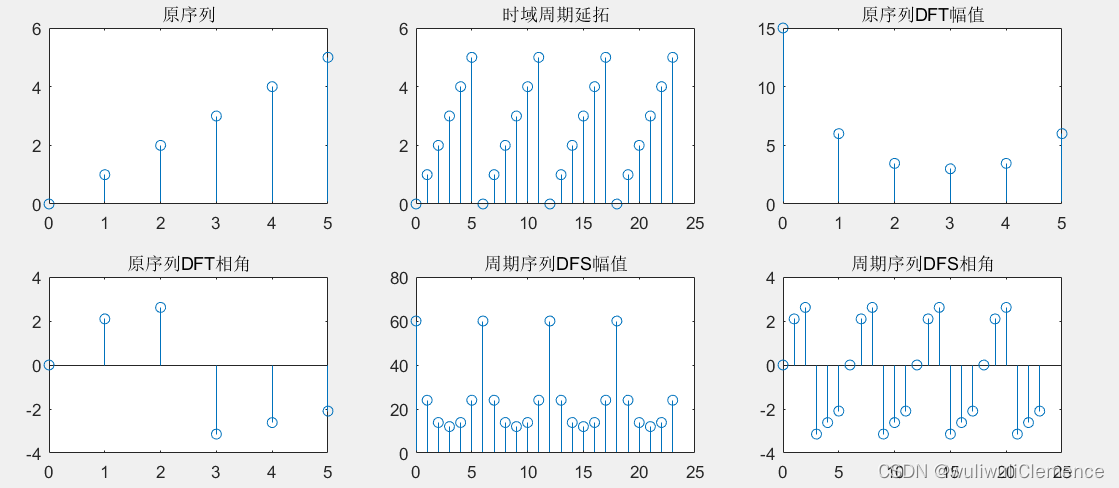
subplot(231);
stem(n0,x0);
title('原序列');
subplot(232);
stem(nn,xn);
title('时域周期延拓');%求原序列的DFT
WN0=exp(-2*j*pi/N0);
X0K=x0*WN0.^(n0'*k0);
subplot(233);
stem(k0,abs(X0K));
title('原序列DFT幅值');
subplot(234);
stem(k0,angle(X0K));
title('原序列DFT相角');%延拓的DFS
WNN=exp(-2*j*pi/N0);
%一定要注意这个地方除N0,虽然进行了周期延拓,但是一个周期上的采样点数,没有变
XNK=xn*(WNN.^(nn'*kn));
subplot(235);
stem(kn,abs(XNK));
title('周期序列DFS幅值');
subplot(236);
stem(kn,angle(XNK));
title('周期序列DFS相角');
XN=dfs(xn,NN);
运行结果:
相关文章:

MATLAB——DFT(离散傅里叶变换)
题目1: 已知有限长序列x(n)为: x(n)[0,1,2,3,4,5,6,7,8,9],求x(n)的DFT和IDFT。要求 1)画出序列傅里叶变换对应的|X(k)|和arg[X(k)]图形。 2)画出原信号与傅里叶逆变换IDFT[X(k)]图形进行比较。 知识点: DF…...

高端Zynq ultrascale+使用GTH回环测试 提供2套工程源码和技术支持
这目录1、前言2、GTH 高速收发器介绍GTH 高速收发器结构参考时钟的选择和分配GTH 发送端GTH 接收端3、vivado工程详解4、上板调试验证5、福利:工程代码的获取1、前言 Xilinx系列FPGA内置高速串行收发器,配有可配置的IP方便用户调用,按照速度…...
)
入门(Createing a scene)
这一部分将对three.js来做一个简要的介绍 首先将开始搭建一个场景,其中包含一个正在旋转的立方体 梦开始的地方 在开始使用threeJS之前,我们需要创建一个HTML文件来显示它(将下列HTML代码保存为你电脑上的一个HTML文件然后在你的浏览器中打…...
Unity入门精要03---透明效果
本节知识架构 1.渲染顺序与渲染队列 如果采用了透明度混合即要是实现半透明效果,那么就要关闭深度写入,那么此时渲染顺序就会变得非常非常重要,不然会出现不正确的遮挡效果。具体的分析可见书中解释 一句话概括就是因为没有写入深度…...

一文解码:如何在人工智能热潮下实现产业“智”变
近期由ChatGPT有关人工智能的话题引发了全民热议,在这股子浪潮下,讨论最多的话题就是ChatGPT的出现会为我们带来怎样的技术变革?是否会改变我们目前的生产方式?对于未来人工智能技术的发展,我们该如何客观看待…...
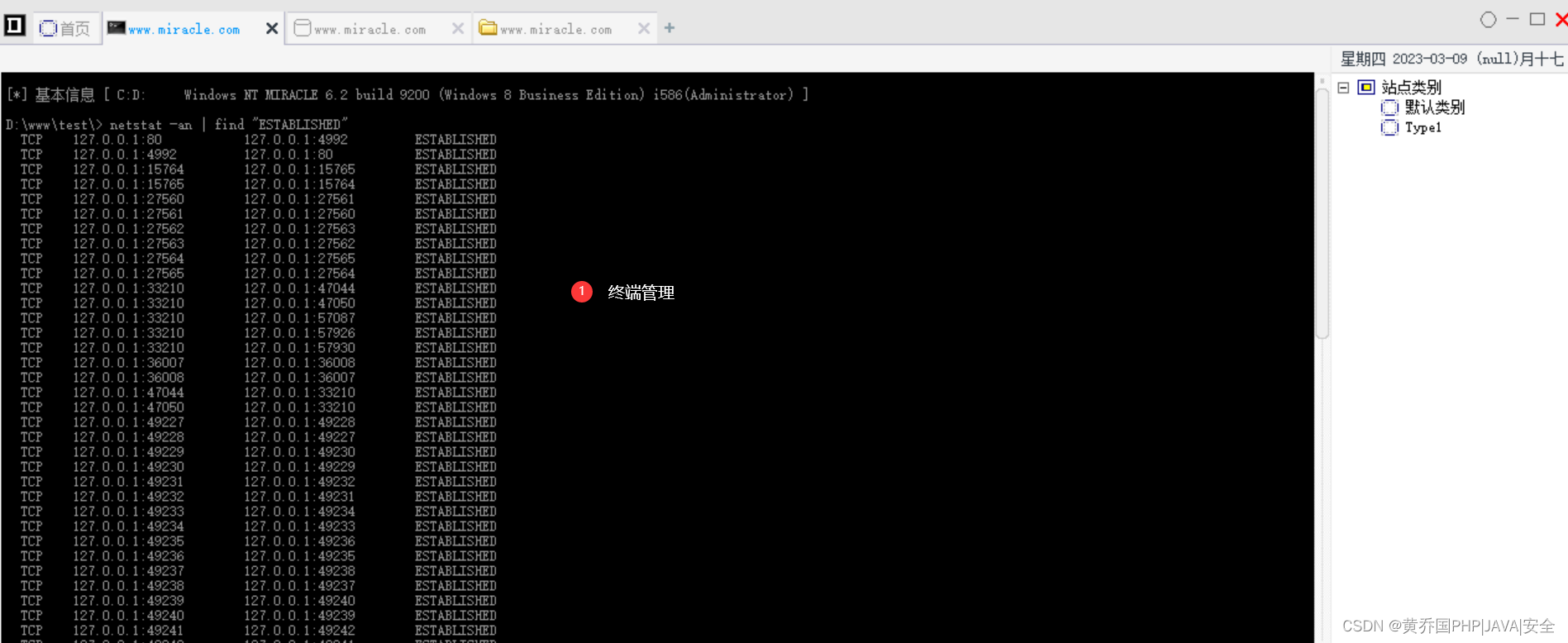
webshell管理工具-菜刀的管理操作
什么是webshell Webshell是一种运行在Web服务器上的脚本程序,通常由黑客使用来绕过服务器安全措施和获取对受攻击服务器的控制权。Webshell通常是通过利用Web应用程序中的漏洞或者弱密码等安全问题而被植入到服务器上的。 一旦Webshell被植入到服务器上࿰…...

dl----算法常识100例
1.depthwise卷积&&Pointwise卷积 depthwise与pointwise卷积又被称为Depthwise Separable Convolution,与常规卷积不同的是此卷积极大地减少了参数数量,同时保持了模型地精度,depthwise操作是先进行二维平面上地操作,然后利…...

京东百亿补贴,不要把方向搞偏了
出品 | 何玺 排版 | 叶媛 我吐槽来了。 3月6日0时,京东正式加入百亿补贴战局。那么,京东百亿补贴力度如何?用户又有什么反馈?我们一起来看看。 01 京东百亿补贴实测 京东百亿补贴上线的第一天,玺哥就亲自进行了体…...

Java中的static与final关键字
一、static关键字 static修饰位置表示含义变量表示这是一个类变量,类加载时分配在堆中方法静态方法,不依赖于对象可直接通过类标识访问代码块静态代码块,只在类加载初始化阶段时执行一次内部类静态嵌套类,表示只是放在外部类的文…...
开学新装备 - 学生党是否该入手 MacBook
学生党是否该入手 macbook 这个问题,相信许多人在许多社区都有看到过类似讨论。只不过,许多讨论都掺杂了信仰、智商税、不懂、不熟悉未来需求等各种因素,导致内容空洞价值不大。这篇文章,抛开了所有非理性因素,详细的告…...

【前端技巧】ESLint忽略检查行和文件
Author:Outman Date:2023-03-10 ESLint忽略检查行和文件 一、注释方式 1.注释忽略 —— 块注释 /* eslint-disable */ console.log(test); /* eslint-enable */2.注释忽略 —— 忽略指定规则项 /* eslint-disable no-alert, no-console */ alert(tes…...

单片机学习笔记之点阵(8x8)
心血来潮,想捡一下丢了很久的单片机,纪录一下单片机学习简单的点阵显示,及踩到的䟘,找到吃灰很久的普中科技开发板(非广告,为毕设学习买的)。 1. 使用工具 使用开发板: 普中科技开发…...
我一个普通程序员,光靠GitHub打赏就年入70万,
一个国外程序员名叫 Caleb Porzio在网上公开了自己用GitHub打赏年入70万的消息和具体做法。 Caleb Porzio 发推庆祝自己靠 GitHub 打赏(GitHub Sponsors)赚到了 10 万美元。 GitHub Sponsors是 GitHub 2019 年 5 月份推出的一个功能,允许开发…...

剖析Spring MVC如何将请求映射到Controller
Spring MVC是一种基于Java的Web框架,可以帮助开发者快速地构建Web应用程序。在Spring MVC中,请求将会被映射到对应的Controller中进行处理。本文将会介绍Spring MVC如何将请求映射到Controller的过程。 DispatcherServlet DispatcherServlet是Spring M…...

设计模式之美-工厂模式
分类:简单工厂模式(静态工厂模式),工厂方法模式,抽象工厂模式。 这种设计模式也是 Java 开发中最常见的一种模式,它的主要意图是定义一个创建对象的接口,让其子类自己决定实例化哪一个工厂类&a…...
A Star算法最通俗易懂的一个版本
01-概述虽然掌握了 A* 算法的人认为它容易,但是对于初学者来说, A* 算法还是很复杂的。02-搜索区域(The Search Area)我们假设某人要从 A 点移动到 B 点,但是这两点之间被一堵墙隔开。如图 1 ,绿色是 A ,红色是 B &…...

JavaWeb--ListenerAjaxaxiosjson
Listener&Ajax&axios1 Listener1.1 概述1.2 分类1.3 代码演示2 Ajax2.1 概述2.1.1 作用2.1.2 同步和异步2.2 快速入门2.2.1 服务端实现2.2.2 客户端实现2.2.3 测试2.3 案例2.3.1 分析2.3.2 后端实现2.3.3 前端实现2.4 测试3 axios3.1 基本使用3.2 快速入门3.2.1 后端实…...
NoneBot2,基于Python的聊天机器人
NoneBot2,基于Python的聊天机器人第一步,配置python第二步,配置[go-cqhttp](https://github.com/Mrs4s/go-cqhttp)第三步,配置[NoneBot](https://61d3d9dbcadf413fd3238e89--nonebot2.netlify.app/)NoneBot2 是一个现代、跨平台、…...

java反射机制及其详解
反射反射机制反射调用优化有时候我们做项目的时候不免需要用到大量配置文件,就拿框架举例,通过这些外部文件配置,在不修改的源码的情况下,来控制文件,就要用到我们的反射来解决 假设有一个Cat对象 public class Cat …...

Leetcode—环形链表
前言:给定一个链表,判断是否为循环链表并找环形链表的入口点 首先我们需要知道什么是双向循环链表,具体如下图所示。 对于链表,我们如何去判断链表是循环链表呢?又寻找入环点呢?我们可以利用快慢指针的方法…...

工程地质软件市场:发展现状、趋势与策略建议
一、引言 在工程建设领域,准确把握地质条件是确保项目顺利推进和安全运营的关键。工程地质软件作为处理、分析、模拟和展示工程地质数据的重要工具,正发挥着日益重要的作用。它凭借强大的数据处理能力、三维建模功能、空间分析工具和可视化展示手段&…...

C++八股 —— 单例模式
文章目录 1. 基本概念2. 设计要点3. 实现方式4. 详解懒汉模式 1. 基本概念 线程安全(Thread Safety) 线程安全是指在多线程环境下,某个函数、类或代码片段能够被多个线程同时调用时,仍能保证数据的一致性和逻辑的正确性…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

Razor编程中@Html的方法使用大全
文章目录 1. 基础HTML辅助方法1.1 Html.ActionLink()1.2 Html.RouteLink()1.3 Html.Display() / Html.DisplayFor()1.4 Html.Editor() / Html.EditorFor()1.5 Html.Label() / Html.LabelFor()1.6 Html.TextBox() / Html.TextBoxFor() 2. 表单相关辅助方法2.1 Html.BeginForm() …...

《Docker》架构
文章目录 架构模式单机架构应用数据分离架构应用服务器集群架构读写分离/主从分离架构冷热分离架构垂直分库架构微服务架构容器编排架构什么是容器,docker,镜像,k8s 架构模式 单机架构 单机架构其实就是应用服务器和单机服务器都部署在同一…...

用js实现常见排序算法
以下是几种常见排序算法的 JS实现,包括选择排序、冒泡排序、插入排序、快速排序和归并排序,以及每种算法的特点和复杂度分析 1. 选择排序(Selection Sort) 核心思想:每次从未排序部分选择最小元素,与未排…...

基于Python的气象数据分析及可视化研究
目录 一.🦁前言二.🦁开源代码与组件使用情况说明三.🦁核心功能1. ✅算法设计2. ✅PyEcharts库3. ✅Flask框架4. ✅爬虫5. ✅部署项目 四.🦁演示效果1. 管理员模块1.1 用户管理 2. 用户模块2.1 登录系统2.2 查看实时数据2.3 查看天…...
