BM25算法以及变种算法简介
深入理解TF-IDF、BM25算法与BM25变种:揭秘信息检索的核心原理与应用
原文链接: https://xie.infoq.cn/article/8b7232877d0d4327a6943e8ac
BM25算法以及变种算法简介
Okapi BM25,一般简称 BM25 算法,在 20 世纪 70 年代到 80 年代,由英国一批信息检索领域的计算机科学家发明。这里的 BM 是 “最佳匹配”(Best Match)的缩写,Okapi 是第一个使用这种方法的信息获取系统的名称。在信息检索领域,BM25 算法是工程实践中举足轻重的重要的 Baseline 算法。迄今为止距 BM25 的提出已经过去三十多年,但是这个算法依然在很多信息检索的任务中表现优异,是很多工程师首选的算法之一。
BM25(Best Match 25)是一种用于信息检索的统计算法,主要用于计算查询文本与文档的相关性评分。它考虑了文档中的词频( T F TF TF)和逆文档频率( I D F IDF IDF)等因素。主要对对 Query 进行语素解析,生成语素 q i q_i qi(词);然后,对于每个搜索结果 d d d,计算每个语素 q i q_i qi 与 d d d 的相关性得分,最后,将 “一个 Q u e r y Query Query各个 q i q_i qi 相对于 d d d 的相关性得分” 加权求和,从而得到“ Q u e r y Query Query 与 d d d 的相关性得分”。
以下是 BM25 的一些重要的变种和衍化算法:
- BM25L(BM25 with Length Normalization):BM25L 算法是在 BM25 算法的基础上,考虑了文档长度对得分的影响,通过引入文档长度规范化项来平衡不同长度的文档,目的是降低文档长度对相关性评分的影响,它可以通过对 BM25 公式中的长度归一化因子进行调整来实现,优化点改进在于更全面地考虑文档特征,以更准确地衡量文档与查询之间的相似度。
- BM25+:BM25+是一种改进的 BM25 算法,加入了查询项权重的计算,以更好地处理查询中的重要词项,这个惩罚项用于调整较长的文档的相关性评分,以避免较长的文档在评分中占据过大的比重。优化点改进在于对查询项的权重进行动态调整,以提高信息检索的准确性和性能。
- BM25T(BM25 with Term Weights):BM25T 是一种将词权重引入 BM25 的方法,通过考虑词频、逆文档频率以及文档长度等特征,以确定每个词项在文本中的重要性,它允许用户为查询中的每个词分配不同的权重,以更好地反映查询的重要性。优化点改进在于更精细地衡量词项的重要性,以提高信息检索的准确性。
- T F 1 ∘ δ ∘ p × I D F TF_{1∘δ∘p}×IDF TF1∘δ∘p×IDF:是一种将词频和词位置信息综合考虑的改进算法。其中,TF表示词频,δ函数表示词位置的影响,p表示词位置权重,IDF表示逆文档频率,通过p和δ来调整词频和逆文档频率的权重,以提高对稀有词项的重视程度。这种算法可以根据词在文档中的位置给予
- BM25F:BM25F 是一种将多个字段考虑在内的改进算法。在信息检索中,通常会有多个字段(如标题、正文、标签等)的相关性需要评分。BM25F 通过对多个字段的评分进行加权求和,可以更好地考虑文档的不同部分对匹配得分的影响,从而得出最终的相关性评分。优化点改进在于更灵活地处理文档的不同部分,以提高信息检索的准确性。
BM25 详解
首先,简单概括 BM25 究竟作何用途。BM25 算法实质上是一个用于信息检索中,对给定查询(query)和若干 “相关” 文档(document)进行相关性排序打分的排序函数。严格来讲,这不是一个打分函数,而是一个家族的一系列评分函数,因为它的提出并非一蹴而就的事情,它的发明经过了若干试验迭代演进。一般情况下,这个相关性打分是一个类似 TF-IDF 的基于统计计数的无监督学习过程。
BM25 算法其主要思想可简述如下:对 query 进行特征提取分解,生成若干特征项(词) q i q_i qi;然后对于每个搜索结果 D,计算每个特征 q i q_i qi与 D 的相关性得分,最后,将 q i q_i qi相对于 D 的相关性得分进行加权求和,从而得到 q u e r y query query与 D D D的相关性得分。
BM25 算法的一般表示可简写为如下形式:
s c o r e ( q , d ) = ∑ i W i ⋅ R ( q i , d ) score(q, d) = \sum_{i} W_i \cdot R(q_i, d) score(q,d)=i∑Wi⋅R(qi,d)
其中, q q q 表示 q u e r y query query, q i q_i qi 表示 q q q 分解之后的一个特征项(对中文而言我们可以把对 query 的分词作为基本特征项), d d d 表示一个搜索结果文档; W i W_i Wi 表示特征 q i q_i qi的权重; R ( q i , d ) R(q_i, d) R(qi,d)表示特征项 q i q_i qi 与文档 d d d 的相关性得分。
上面这个一般的式子里的 $W_i 和 和 和R(q_i, d)$ 的具体计算,都是基于词袋方法的词频计数,它不考虑多个搜索词在文档里的关联性,只考虑它们各自的出现次数。
下面我们来考察以上得分函数的两个量 $W_i $和 R ( q i , d ) R(q_i, d) R(qi,d) 该如何设计和计算。
首先来看如何定义 W i W_i Wi,考察一个特征词的权重,方法比较多,较常用的是 IDF,BM25 选择的是 Robertson-Sparck Jones IDF:
IDF ( q i ) = log N − n ( q i ) + 0.5 n ( q i ) + 0.5 \text{IDF}(q_i) = \log \frac{N - n(q_i) + 0.5}{n(q_i) + 0.5} IDF(qi)=logn(qi)+0.5N−n(qi)+0.5
其中, N N N 为文档集合中的全部文档数, n ( q i ) n(q_i) n(qi) 为包含 q i q_i qi 的文档数。 I D F IDF IDF 公式指出, q i q_i qi 出现在越多的文档中,则 q i q_i qi 的权重则越低。这里个定义有个问题,那就是,如果一个词在超过半数的文档里出现,则 I D F IDF IDF 为负值,于是这个词对 BM25 分数的贡献是负的。一般不希望这样的特性,所以当 I D F IDF IDF 为负数时,可将其置为 0,或者一个比较小的正数,或者改用一种平滑过渡到 0 的函数形式。
我们再来考察特征项 $q_i $与文档 d d d 的相关性得分 R ( q i , d ) R(q_i, d) R(qi,d)。
比较朴素的考虑可以用特征词的文档词频来简单表示 R ( q i , d ) R(q_i, d) R(qi,d),但这种直观的想法不可避免导致长文本中,词的频度普遍较高,最终相关性得分会过度倾向于长文本,显然不尽合理;另一方面,不难想象到,某个词对文档的贡献不应该无限度地随词频增长而线性增加,当该词的词频高于某个程度就应该趋于饱和,而不应该让其得分贡献无限度增大,从而在整个得分求和式子中占支配地位。
基于以上两方面的考虑,BM25 采取了以下方式来计算 R ( q i , d ) R(q_i, d) R(qi,d):
R ( q i , d ) = ( k 1 + 1 ) ⋅ t f ~ ( q i , d ) k 1 + t f ~ ( q i , d ) R(q_i, d) = \frac{(k_1 + 1) \cdot \tilde{tf}(q_i, d)}{k_1 + \tilde{tf}(q_i, d)} R(qi,d)=k1+tf~(qi,d)(k1+1)⋅tf~(qi,d)
t f ~ ( q i , d ) = t f ( q i , d ) 1 + b ( L d L a v g − 1 ) \tilde{tf}(q_i, d) = \frac{tf(q_i, d)}{1+ b(\frac{L_d}{L_{avg}} - 1)} tf~(qi,d)=1+b(LavgLd−1)tf(qi,d)
这里, f ( q i , d ) f(q_i, d) f(qi,d) 为$ q_i$ 在 d d d 中的文档频率, L d L_d Ld 为文档长度, L a v g L_{avg} Lavg 为文档集合中的平均长度, k 1 k_1 k1 和 b b b 为可自由调节的超参数,一般取值范围是 k 1 ∈ [ 1.2 , ; 2.0 ] k_1 \in [1.2,;2.0] k1∈[1.2,;2.0], b = 0.75 , R ( q i , d ) b = 0.75,R(q_i, d) b=0.75,R(qi,d) 关于$ \tilde{tf}(q_i, d)$ 的函数是一个 “饱和” 的递增函数,使得文档词频增长对相关性得分增长成为非线性的。
从$ \tilde{tf}(q_i, d)$ 的定义中不难看出,超参数 k 1 k_1 k1 起着调节特征词文本频率尺度的作用, k 1 k_1 k1 取 0 0 0 意味着算法退化为二元模型(不考虑词频),而取较大的值则近似于只用原始的特征词频。超参数 b b b 一般称作文本长度的规范化,作用是调整文档长度对相关性影响的大小。 b b b 越大,文档长度的对相关性得分的影响越大,而文档的相对长度越长, t f ~ ( q i , d ) \tilde{tf}(q_i, d) tf~(qi,d) 值将越大,则相关性得分会越小。这可以理解为,当文档相对较长时,包含 q i q_i qi 的机会越大,因此,同等 t f ( q i , d ) tf(q_i, d) tf(qi,d) 的情况下,长文档与 q i q_i qi 的相关性应该比短文档与 q i q_i qi 的相关性弱。
至此,综合上述讨论,BM25 的一般形式可完整表示如下:
s c o r e ( q , d ) = ∑ i log N − n ( q i ) + 0.5 n ( q i ) + 0.5 ⋅ ( k 1 + 1 ) ⋅ t f ( q i , d ) k 1 ( 1 − b + b ⋅ L d L a v g ) + t f ( q i , d ) score(q, d) = \sum_i \log \frac{N - n(q_i) + 0.5}{n(q_i) + 0.5} \cdot \frac{(k_1 + 1) \cdot tf(q_i, d)}{k_1(1 - b + b\cdot \frac{L_d}{L_{avg}}) + tf(q_i, d)} score(q,d)=i∑logn(qi)+0.5N−n(qi)+0.5⋅k1(1−b+b⋅LavgLd)+tf(qi,d)(k1+1)⋅tf(qi,d)
此外,若 query 比较长,且某些 term 在 query 中出现频率较高,我们理应考虑这些 term 的重要性也该相应提高,但同样应该有类似 term 相对文档的饱和增长设置来约束 query 中的 term 频率增长。这里我们将类似的权重策略用于 query 中的特征项,得到:
s c o r e ( q , d ) = ∑ i log N − n ( q i ) + 0.5 n ( q i ) + 0.5 ⋅ ( k 1 + 1 ) ⋅ t f ( q i , d ) k 1 ( 1 − b + b ⋅ L d L a v g ) + t f ( q i , d ) ⋅ ( k 3 + 1 ) ⋅ t f ( q i , q ) k 3 + t f ( q i , q ) score(q, d) = \sum_i \log \frac{N - n(q_i) + 0.5}{n(q_i) + 0.5} \cdot \frac{(k_1 + 1) \cdot tf(q_i, d)}{k_1(1 - b + b\cdot \frac{L_d}{L_{avg}}) + tf(q_i, d)} \cdot \frac{(k_3 + 1)\cdot tf(q_i, q)}{k_3 + tf(q_i, q)} score(q,d)=i∑logn(qi)+0.5N−n(qi)+0.5⋅k1(1−b+b⋅LavgLd)+tf(qi,d)(k1+1)⋅tf(qi,d)⋅k3+tf(qi,q)(k3+1)⋅tf(qi,q)
其中, t f ( q i , q ) tf(q_i, q) tf(qi,q) 为特征项 q i q_i qi 在查询 q q q 中的频率,超参数 k 3 k_3 k3 的作用依然是调节特征词在 query 文本频率尺度,此时对 query 进行长度规范化却是不必要的,因为对所有候选检索结果而言,query 是先有的固定好的。
从以上对 BM25 的完整讨论,我们知道了 BM25 其实是一个(准确说,是一系列)经验公式,这里面的每一个环节都是经过很多研究者的迭代而逐步发现的。很多研究在理论上对 BM25 进行了建模,从 “概率相关模型”(Probabilistic Relevance Model)入手,推导出 BM25 其实是对某一类概率相关模型的逼近,对此我还没有详尽研究,就无法进一步展开论述了。从结果上看,我们应该明了 BM25 权重计算公式,已经在众多的数据集和搜索任务上,被极其高频广泛和成功地使用。
BM25算法简易
一条 Query 与搜索结果的任意 doc 之间相关性分数:
S c o r e ( Q , d ) = ∑ i n W i R ( q i , d ) Score(Q,d)=\sum\limits_{i}^n W_i R(q_i, d) Score(Q,d)=i∑nWiR(qi,d)
上式, Q Q Q 表示 Q u e r y Query Query, q i q_i qi 表示根据 Q Q Q 解析获得的语素, d d d 表示搜索结果的一条文档, W i W_i Wi 表示语素 q_i的权重, R(q_i, d)表示q_i和d的相关性得分。
(1) W_i的定义
定义一个语素与一个文档的相关性权重,较常用的是
I D F ( q i ) = l o g N − n ( q i ) + 0.5 n ( q i ) + 0.5 IDF(q_i)=log\frac{N-n(q_i)+0.5}{n(q_i)+0.5} IDF(qi)=logn(qi)+0.5N−n(qi)+0.5
上式, N N N 是索引中的全部文档数, n ( q i ) n(q_i) n(qi)是包含 q i q_i qi的文档数。
很显然, n ( q i ) n(q_i) n(qi)与 I D F ( q i ) IDF(q_i) IDF(qi)成反相关,即当给定的文档集合里,很多文档都包含 q i q_i qi时, q i q_i qi的区分度就不高,则使用 q i q_i qi来判断相关性的重要度就较低。
(2) R ( q i , d ) R(q_i, d) R(qi,d) 的定义
定义一个语素与一个文档的相关性得分,一般形式如下
R ( q i , d ) = f i ( k 1 + 1 ) f i + K q f i ( k 2 + 1 ) q f i + k 2 R(q_i, d)=\frac{f_i (k_1 +1)}{f_i + K}\frac{qf_i (k_2 +1)}{qf_i + k_2} R(qi,d)=fi+Kfi(k1+1)qfi+k2qfi(k2+1)
K = k 1 ( 1 − b + b d l a v g d l ) K=k_1(1-b+b\frac{dl}{avgdl}) K=k1(1−b+bavgdldl)
上式 k 1 k_1 k1 , k 2 k_2 k2 , b b b 是可根据经验设置的调节因子,一般 k 1 ∈ [ 1.2 , 2 ] k_1\in[1.2,2] k1∈[1.2,2] , b = 0.75 b=0.75 b=0.75 ; f i f_i fi 是 q i q_i qi 在 d d d 中出现的频率, q f i qf_i qfi 为 q i q_i qi 在 Q Q Q 中的出现频率。 d l dl dl 为 d d d 的长度, a v g d l avgdl avgdl 为文档集中所有 d d d 的平均长度。在多数情况下, q i q_i qi 在 Q Q Q中只会出现一次,即 q f i = 1 qf_i=1 qfi=1,公式可简化为:
R ( q i , d ) = f i ( k 1 + 1 ) f i + K R(q_i, d)=\frac{f_i (k_1 +1)}{f_i + K} R(qi,d)=fi+Kfi(k1+1)
由 K 的表达式可知, b b b的作用是调整 d l dl dl对 “相关性的影响” 的大小,即 b b b越大, d l dl dl对 “相关性得分的影响” 越大;而 d l dl dl越长, K K K 值越大,相关性得分越小。
可如下解释,当文档较长时,包含 q i q_i qi的机会越大,则同等 f i f_i fi的情况下,“长文档与 q i q_i qi的相关性” 应该比 “短文档与 q i q_i qi的相关性” 弱。
BM25 的变种和改进
BM25 算法公式,通过使用不同的特征项的分析方法、特征项权重判定方法,以及特征项与文档的相关度计算方法,都留有较强的灵活性,自然会促使后续的研究者在此基础上,提出更具个性化的不同的搜索相关性得分算法。
所有 BM25 后续改进中,Lv & Zhai 两位研究者的工作最为深入和全面。
BM25L
Lv & Zhai 观察到 BM25 公式中的文本长度规范化项(L_d/L_{avg})使得模型得分过于偏好长度较短的文档。他们在 “When documents are very long, BM25 fails!” 一文中提出了 BM25L 算法,用来弥补 BM25 的这一不足。
首先,BM25L 对特征词的 IDF 权重项也做了小小改变,让这一项不会取到负值:
IDF ( q i ) = log N + 1 n ( q i ) + 0.5 \text{IDF}(q_i) = \log \frac{N + 1}{n(q_i) + 0.5} IDF(qi)=logn(qi)+0.5N+1
然而,BM25L 更感兴趣的是调节 BM25 中 t f ~ ( q i , d ) \tilde{tf}(q_i, d) tf~(qi,d)这一项,以避免算法对过长文本的惩罚。Lv & Zhai 通过对 t f ~ ( q i , d ) \tilde{tf}(q_i, d) tf~(qi,d)加上一个正值的常数 δ \delta δ来实现这一点,只需这一个小操作便可以起到让 t f ~ ( q i , d ) \tilde{tf}(q_i, d) tf~(qi,d)与之前比较,向偏好取更小的值转移(即较大的分母,较长的文本)。
因此,可将 BM25L 算法写作如下:
s c o r e ( q , d ) = ∑ i log N + 1 n ( q i ) + 0.5 ⋅ ( k 1 + 1 ) ⋅ ( t f ~ ( q i , d ) + δ ) k 1 + t f ~ ( q i , d ) + δ score(q, d) = \sum_i \log \frac{N + 1}{n(q_i) + 0.5} \cdot \frac{(k_1 + 1) \cdot (\tilde{tf}(q_i, d) + \delta )}{k_1 + \tilde{tf}(q_i, d) + \delta} score(q,d)=i∑logn(qi)+0.5N+1⋅k1+tf~(qi,d)+δ(k1+1)⋅(tf~(qi,d)+δ)
同 BM25 公式记号保持一致,这里
t f ~ ( q i , d ) = t f ( q i , d ) 1 + b ( L d L a v g − 1 ) \tilde{tf}(q_i, d) = \frac{tf(q_i, d)}{1+ b(\frac{L_d}{L_{avg}} - 1)} tf~(qi,d)=1+b(LavgLd−1)tf(qi,d)
BM25+
Lv & Zhai 进一步发现对过长文本的惩罚不止出现在 BM25 算法中,还出现在许多其他的排序函数中,他们为此提出了一个一般性的解决方案,即为每一个 query 中出现于文本的特征项相关性得分设置一个下界。此时,不论文本多长,某个搜索特征项至少贡献了一个正的常数相关性得分。他们这个做法略不同于之前的 BM25L,而是在乘 IDF 之前对整个 R ( q i , d ) R(q_i, d) R(qi,d) 加上一个常数 δ \delta δ:
s c o r e ( q , d ) = ∑ i log N + 1 n ( q i ) + 0.5 ⋅ ( ( k 1 + 1 ) ⋅ t f ~ ( q i , d ) k 1 + t f ~ ( q i , d ) + δ ) score(q, d) = \sum_i \log \frac{N + 1}{n(q_i) + 0.5} \cdot \left(\frac{(k_1 + 1) \cdot \tilde{tf}(q_i, d)}{k_1 + \tilde{tf}(q_i, d)} + \delta \right) score(q,d)=i∑logn(qi)+0.5N+1⋅(k1+tf~(qi,d)(k1+1)⋅tf~(qi,d)+δ)
BM25-adpt
之前的 BM25 算法和相关改进,都忽略了对超参数 k 1 k_1 k1 的考察。Lv & Zhai 在不同的 BM25 相关研究工作中,发现对实际应用而言,全局的 k 1 k_1 k1 参数不及特征项相关的(term-specific) k 1 k_1 k1参数使用起来高效。他们用随机理论中的信息增益和散度等概念,实现了 k 1 k_1 k1去 “超参化” 的目标,即 k 1 k_1 k1 跟随 t e r m term term 不同而变化,可以直接计算获得,这个算法被称为 BM25-adpt。BM25-adpt 的具体推导比上面的 BM25 变种算法要稍微复杂一些,要讲清楚其中的想法和细节,需要另辟篇幅,只好以后得空的时候补缀上,这里就不能多加介绍了。
小结
除了以上探讨的几种 BM25 的衍化算法,其他重要的变种还有 BM25T、TF1∘δ∘p×IDF\text{TF}_{1\circ\delta\circ p}\times \text{IDF}、BM25F 等等,在许多不同的场景都表现除了优于原始 BM25 算法的效果。当然,这些表现的优越性因具体数据集和相应 search 任务场景而异。
更多优质内容请关注公号:汀丶人工智能;会提供一些相关的资源和优质文章,免费获取阅读。
参考链接:
bm25 算法:https://blog.csdn.net/cymy001/article/details/91972337.
Okapi BM25 算法:https://www.cnblogs.com/geeks-reign/p/Okapi_BM25.html
TF-IDF 算法 https://www.cnblogs.com/geeks-reign/p/TF-IDF.html
[1]. wikipedia: Okapi_BM25, https://en.wikipedia.org/wiki/Okapi_BM25.
[2]. Okapi BM25: a non-binary model, https://nlp.stanford.edu/IR-book/html/htmledition/okapi-bm25-a-non-binary-model-1.html.
[3]. Trotman, A., Puurula, A. Burgess, B., Improvements to BM25 and Language Models Examined.
[4]. Lv, Y., C. Zhai, When documents are very long, BM25 fails! SIGIR 2011, p. 1103-1104.
[5]. Lv, Y., C. Zhai, Lower-bounding term frequency normalization, CIKM 2011, p. 7-16.
[6]. Lv, Y., C. Zhai, Adaptive term frequency normalization for BM25, CIKM 2011, p. 1985-1988.
相关文章:

BM25算法以及变种算法简介
深入理解TF-IDF、BM25算法与BM25变种:揭秘信息检索的核心原理与应用 原文链接: https://xie.infoq.cn/article/8b7232877d0d4327a6943e8ac BM25算法以及变种算法简介 Okapi BM25,一般简称 BM25 算法,在 20 世纪 70 年代到 80 年代…...
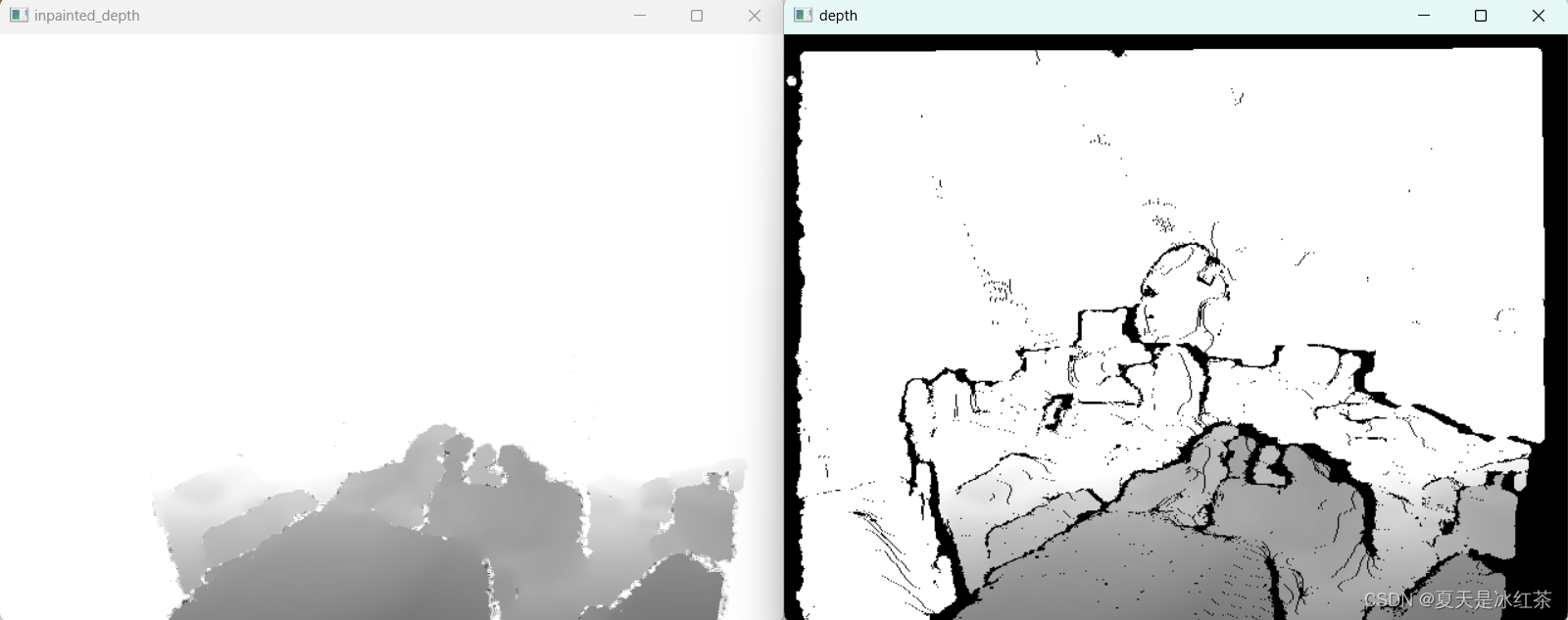
D455相机RGB与深度图像对齐,缓解相机无效区域的问题
前言 上一次我们介绍了深度相机D455的使用:intel深度相机D455的使用-CSDN博客,我们也看到了相机检测到的无效区域。 在使用Intel深度相机D455时,我们经常会遇到深度图中的无效区域。这些无效区域可能由于黑色物体、光滑表面、透明物体以及视…...
2024 cicsn ezbuf
文章目录 参考protobuf逆向学习复原结构思路exp 参考 https://www.y4ng.cn/posts/pwn/protobuf/#ciscn-2024-ezbuf protobuf 当时压根不知道用了protobuf这个玩意,提取工具也没提取出来,还是做题做太少了,很多关键性的结构都没看出来是pro…...

地面站Mission planner
官方教程; Mission Planner地面站介绍 | Autopilot (gitbook.io) Mission Planner 功能/屏幕 — Mission Planner 文档 (ardupilot.org) 安卓或者windows软件下载地址: 地面站连接及使用 plane (cuav.net) 在完全装机后再进行各干器件的校准,没有组…...
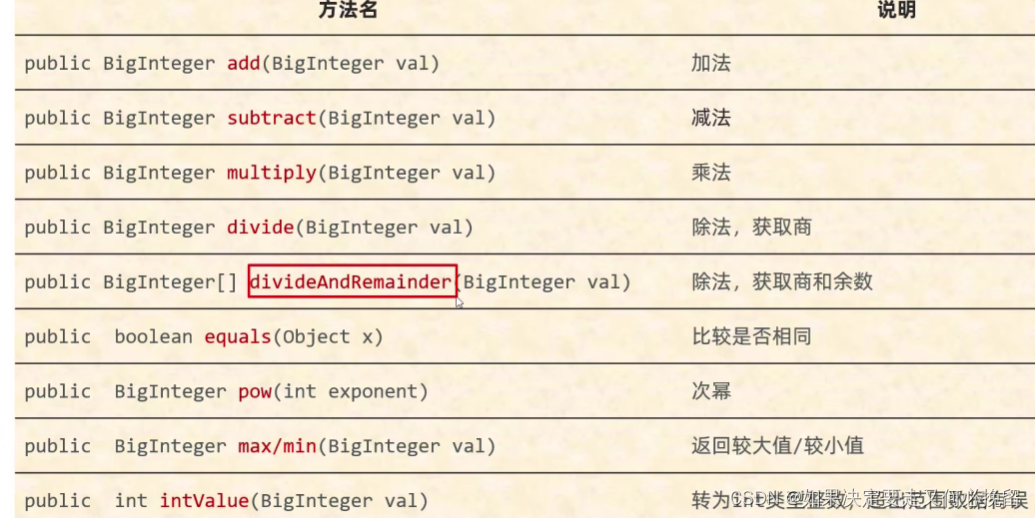
常见的api: BigInteger
一.获取一个大的随机整数 1.代码: BigInteger bd1 new BigInteger(4, new Random());System.out.println(bd1); 2.打印的结果:2 3.注释获取的是0-16之间的随机整数 二.获取一个指定的大的数 1.代码: BigInteger bd2 new BigInteger("100");System.o…...

Overall timing accuracy 和Edge placement accuracy 理解
在电子设计自动化(EDA)、集成电路(IC)制造和高速数字电路设计领域,"Overall Timing Accuracy" 和 "Edge Placement Accuracy" 是两个关键的性能指标,它们对于确保电路的功能正确性和性能至关重要。 当涉及到“Overall timing accuracy”(总体时序精度)…...
2024 vite 静态 scp2 自动化部署
1、导入库 npm install scp2 // 自动化部署 npm install chalk // 控制台输出的语句 npm install ora2、核心代码 创建文件夹放在主目录下的 deploy/index.js 复制粘贴以下代码: import client from scp2; import chalk from chalk; import ora from ora;const s…...
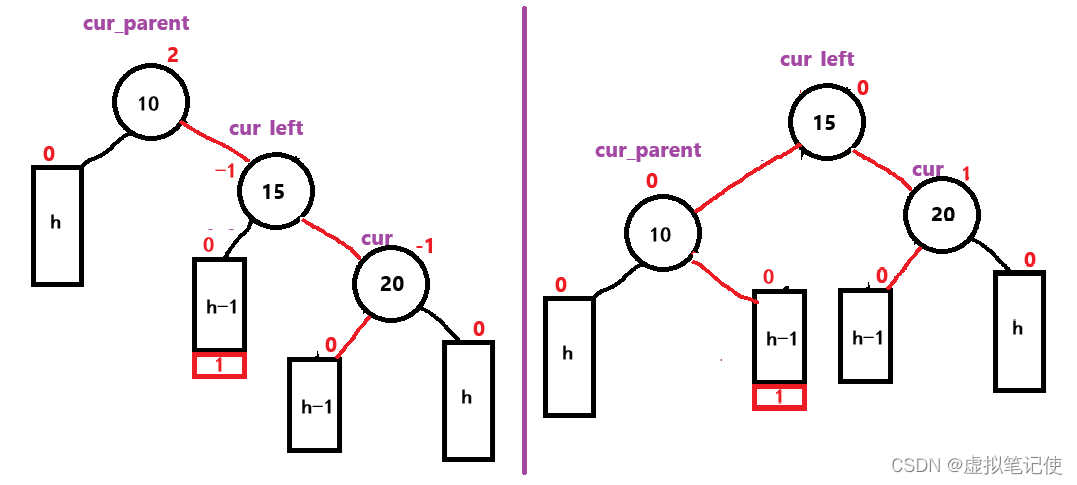
【数据结构】AVLTree实现详解
目录 一.什么是AVLTree 二.AVLTree的实现 1.树结点的定义 2.类的定义 3.插入结点 ①按二叉搜索树规则插入结点 ②更新平衡因子 更新平衡因子情况分析 ③判断是否要旋转 左单旋 右单旋 左右单旋 右左双旋 4.删除、查找和修改函数 查找结点 三.测试 1.判断是否是搜索树 …...
深度学习——TensorBoard的使用
官方文档torch.utils.tensorboard — PyTorch 2.3 documentation TensorBoard简介 TensorBoard是一个可视化工具,它可以用来展示网络图、张量的指标变化、张量的分布情况等。特别是在训练网络的时候,我们可以设置不同的参数(比如࿱…...
⭐⭐⭐)
【设计模式】观察者模式(行为型)⭐⭐⭐
文章目录 1.概念1.1 什么是观察者模式1.2 优点与缺点 2.实现方式3. Java 哪些地方用到了观察者模式4. Spring 哪些地方用到了观察者模式 1.概念 1.1 什么是观察者模式 观察者模式(Observer Pattern)是一种行为型设计模式,它允许对象在状态改…...

轻松搞定阿里云域名DNS解析
本文将会讲解如何设置阿里云域名DNS解析。在进行解析设置之前,你需要提前准备好需要设置的云服务器IP地址、域名以及CNAME记录。 如果你还没有云服务器和域名,可以参考下面的方法注册一个。 申请域名:《Namesilo域名注册》注册云服务器&…...

GAT1399协议分析(10)--单图像删除
一、官方接口 由于批量删除的接口,图像只能单独删除。 二、wireshark实例 这个接口比较简单,调用request delete即可 文本化: DELETE /VIID/Images/34078100001190001002012024060513561300065 HTTP/1.1 Host: 10.0.201.56:31400 User-Age…...

Hudi CLI 安装配置总结
前言 上篇文章 总结了Spark SQL Rollback, Hudi CLI 也能实现 Rollback,本文总结下 Hudi CLI 安装配置以及遇到的问题。 官方文档 https://hudi.apache.org/cn/docs/cli/ 版本 Hudi 0.13.0(发现有bug)、(然后升级)0.14.1Spark 3.2.3打包 mvn clean package -DskipTes…...
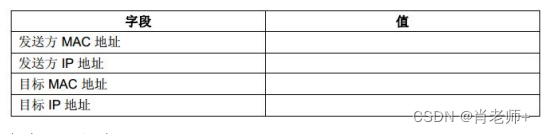
实验八、地址解析协议《计算机网络》
水逆退散,学业进步,祝我们都好,不止在夏天。 目录 一、实验目的 二、实验内容 (1)预备知识 (2)实验步骤 三、实验小结 一、实验目的 完成本练习之后,您应该能够确定给定 IP 地…...

Linux系统管理磁盘管理003
操作系统: CentOS Stream9 测试过程: 模拟磁盘被沾满, 创建文件 测试脚本 for i in seq 10do# echo $idd if/dev/zero of./$i-$RANDOM.txt bs1M count1024 Done[rootlocalhost ~]# vim 2.txt [rootlocalhost ~]# sh 2.txt 记录了10240 的…...

MLC工具是否适用AMD和ARM场景?如何测试内存性能?
MLC(Memory Latency Checker)主要是由Intel开发的工具,主要用于Intel平台上的内存性能测试,尤其是针对Intel处理器的内存延迟和带宽。尽管MLC主要针对Intel处理器设计,理论上它可以在任何支持Intel兼容指令集的系统上运…...

NodeJs实现脚本:将xlxs文件输出到json文件中
文章目录 前期工作和依赖笔记功能代码输出 最近有一个功能,将json文件里的内容抽取到一个xlxs中,然后维护xlxs文件。当要更新json文件时,就更新xlxs的内容并把它传回json中。这个脚本主要使用NodeJS写。 以下是完成此功能时做的一些笔记。 …...

【启程Golang之旅】网络编程与反射
欢迎来到Golang的世界!在当今快节奏的软件开发领域,选择一种高效、简洁的编程语言至关重要。而在这方面,Golang(又称Go)无疑是一个备受瞩目的选择。在本文中,带领您探索Golang的世界,一步步地了…...

nginx location正则表达式+案例解析
1、nginx常用的正则表达式 ^ :匹配输入字符串的起始位置$ :匹配输入字符串的结束位置 *:匹配前面的字符零次或多次。如“ol*”能匹配“o”及“ol”、“oll” :匹配前面的字符一次或多次。如“ol”能匹配“ol”及“oll”、“olll”…...

【YOLO系列】YOLOv10论文超详细解读(翻译 +学习笔记)
前言 研究AI的同学们面对的一个普遍痛点是,刚开始深入研究一项新技术,没等明白透彻,就又迎来了新的更新版本——就像我还在忙着逐行分析2月份发布的YOLOv9代码,5月底清华的大佬们就推出了全新的v10。。。 在繁忙之余࿰…...

简易版抽奖活动的设计技术方案
1.前言 本技术方案旨在设计一套完整且可靠的抽奖活动逻辑,确保抽奖活动能够公平、公正、公开地进行,同时满足高并发访问、数据安全存储与高效处理等需求,为用户提供流畅的抽奖体验,助力业务顺利开展。本方案将涵盖抽奖活动的整体架构设计、核心流程逻辑、关键功能实现以及…...

【网络安全产品大调研系列】2. 体验漏洞扫描
前言 2023 年漏洞扫描服务市场规模预计为 3.06(十亿美元)。漏洞扫描服务市场行业预计将从 2024 年的 3.48(十亿美元)增长到 2032 年的 9.54(十亿美元)。预测期内漏洞扫描服务市场 CAGR(增长率&…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

【JavaWeb】Docker项目部署
引言 之前学习了Linux操作系统的常见命令,在Linux上安装软件,以及如何在Linux上部署一个单体项目,大多数同学都会有相同的感受,那就是麻烦。 核心体现在三点: 命令太多了,记不住 软件安装包名字复杂&…...

CMake控制VS2022项目文件分组
我们可以通过 CMake 控制源文件的组织结构,使它们在 VS 解决方案资源管理器中以“组”(Filter)的形式进行分类展示。 🎯 目标 通过 CMake 脚本将 .cpp、.h 等源文件分组显示在 Visual Studio 2022 的解决方案资源管理器中。 ✅ 支持的方法汇总(共4种) 方法描述是否推荐…...

排序算法总结(C++)
目录 一、稳定性二、排序算法选择、冒泡、插入排序归并排序随机快速排序堆排序基数排序计数排序 三、总结 一、稳定性 排序算法的稳定性是指:同样大小的样本 **(同样大小的数据)**在排序之后不会改变原始的相对次序。 稳定性对基础类型对象…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

《Offer来了:Java面试核心知识点精讲》大纲
文章目录 一、《Offer来了:Java面试核心知识点精讲》的典型大纲框架Java基础并发编程JVM原理数据库与缓存分布式架构系统设计二、《Offer来了:Java面试核心知识点精讲(原理篇)》技术文章大纲核心主题:Java基础原理与面试高频考点Java虚拟机(JVM)原理Java并发编程原理Jav…...
