【数据结构】AVLTree实现详解
目录
一.什么是AVLTree
二.AVLTree的实现
1.树结点的定义
2.类的定义
3.插入结点
①按二叉搜索树规则插入结点
②更新平衡因子
更新平衡因子情况分析
③判断是否要旋转
左单旋
右单旋
左右单旋
右左双旋
4.删除、查找和修改函数
查找结点
三.测试
1.判断是否是搜索树
2.判断每一个结点的左右子树高度差是否不大于1
四.所有源代码
AVLTree.h
Test.c
在本篇博客中,作者将会使用C++来带领你理解和实现AVLTree,同时,在学习AVLTree之
前,你可以先看看下面这篇二叉搜索树的博客,因为AVTree也是一种二叉搜索树,它们有一些规则是一样的。
【C++】二叉搜索树-CSDN博客
一.什么是AVLTree
在二叉搜索树的博客中,我们提到了,当插入的数据有序或者接近有序的时候,二叉搜索树会退化成单支树,导致其效率变低,所以为了解决这种情况,于是我们提出了AVLTree,即二叉平衡搜索树。
如下图就是一棵二叉搜索树退化成的单支树。
那么AVLTree又是如何实现使二叉树搜索树不会退化成单支树的呢,它又是如何保证效率的呢?
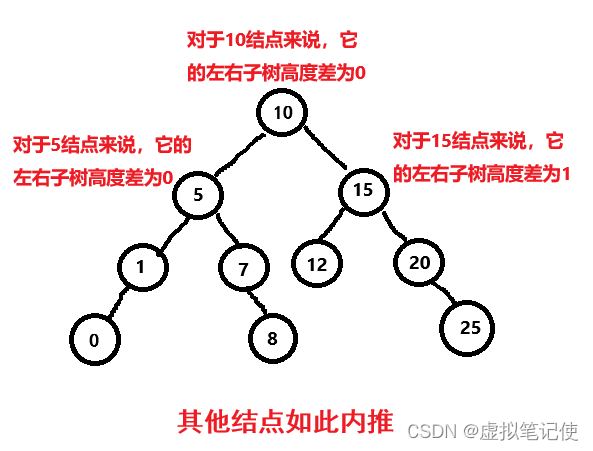
因为AVLTree严格的要求左右子树的高度差不能大于1,且每一棵子树也一样。 如下图所示。
通过这样严格的高度差要求,该树就可以达到一个非常平衡的状态,以致于它的插入、删除、查找等操作的效率非常的高,其时间复杂度就是O(logN),N为结点的个数。
那么它又是如何实现这样的要求的?
前面说了,AVLTree保证了每个结点的左右子树的高度差不大于1,那是因为当有一个结点的左右子树高度差为2时,它会进行旋转,使其保证平衡,至于怎么旋转,我们接着往下看。
二.AVLTree的实现
知道了AVLTree的规则,那么我们就可以来实现一下AVLTree了。
1.树结点的定义
在树结点的定义中,对比平常的二叉树,多了两个变量,一个是父结点的指针_parent,一个是_bf平衡因子。
其中_parent指针是方便我们在后续的操作中,去倒着往上去找父结点。
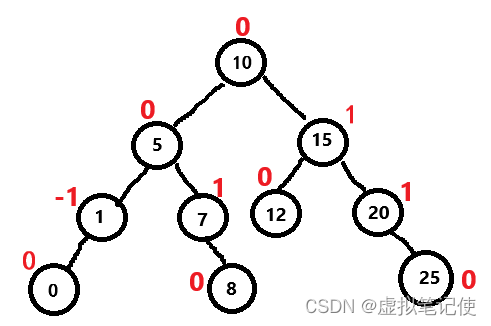
_bf平衡因子是存储该结点的左右子树的高度差,这里默认为右子树的高度减去左子树的高度,通过_bf平衡因子,我们可以很快的知道该结点下的树是否平衡。
template<class T>struct TreeNode{//成员变量T _data;//树结点存储的数据类型TreeNode<T>* _left;//左孩子指针TreeNode<T>* _right;//右孩子指针TreeNode<T>* _parent;//父结点指针int _bf;//平衡因子//成员函数TreeNode(cosnt T& tmp)//构造函数:_data(tmp), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}};对于平衡因子来说,如下图所示。
_bf平衡因子=右子树的高度 - 左子树的高度
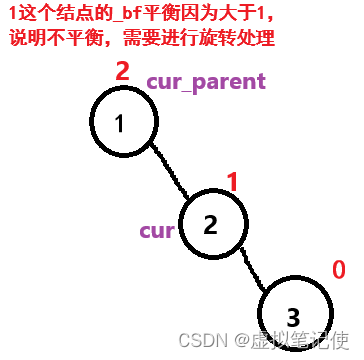
当_bf平衡因子的绝对值大于1时,说明该结点的左右子树高度差大于1,这个时候需要进行旋转处理。如下图所示。
2.类的定义
对于类的定义,就比较简单,就是一个_root指针指向根节点。
template<class T>class AVLTree{typedef TreeNode<T> Node;public://构造函数AVLTree():_root(nullptr){}private:Node* _root;//根节点的指针};3.插入结点
对于AVLTree来说,最重要的就是插入结点,同时,这也是比较难的一部分,代码也比较长,但是不要怕,我们把AVLTree的插入分成如下几个部分。
1.先按二叉搜索树的规则插入结点,就是先不管三七二十一,先把结点插入进去再说。
至于二叉搜索树的插入,可以看开头的博客链接。
2.更新平衡因子,插入新结点后会影响平衡因子,所以插入新结点后,要更新平衡因子。
3.判断是否要旋转,更新完平衡因子后,要判断直接结束了还是要进行旋转调整。
接下来我们要把上面的三个过程转换成代码,这里代码会有点长,我们把这个insert函数分成三部分来说。如下是这个函数的函数名和参数。tmp为要插入的值。
bool insert(const T& tmp)①按二叉搜索树规则插入结点
对于这一部分来说,没那么难,整个插入过程如下图所示。
就是用tmp从根结点开始进行比较,一直往下找空位,找到空位后,再把结点插入进去。
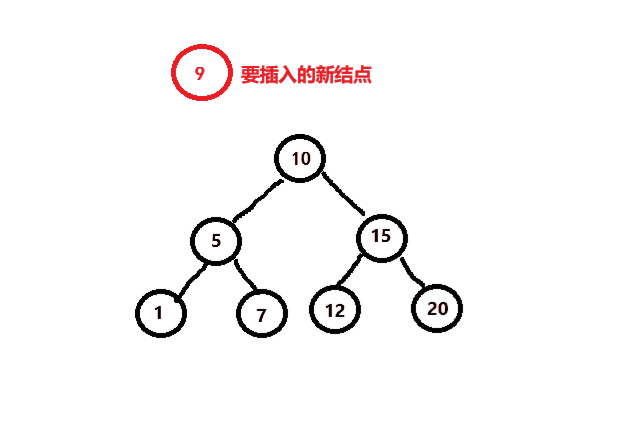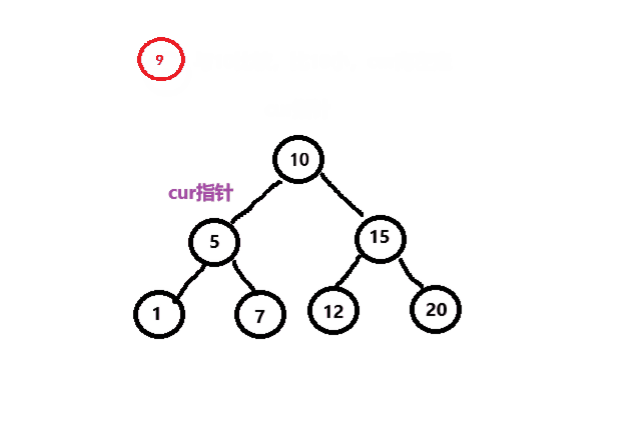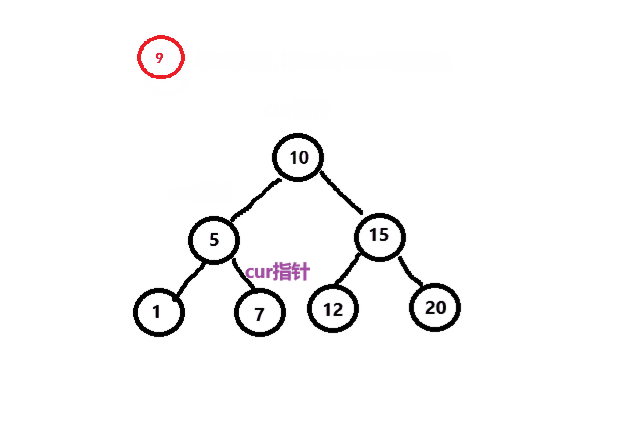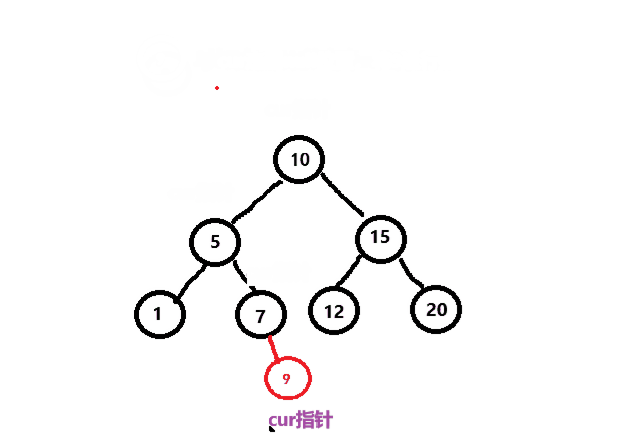
//如果根节点为空,则直接插入if (_root == nullptr){_root = new Node(tmp);return true;}//如果根节点不为空,则先按二叉搜索树的规则进行插入Node* cur = _root;Node* cur_parent = nullptr;while (cur != nullptr)//往下找空位{if (tmp > cur->_data){cur_parent = cur;cur = cur->_right;}else if (tmp < cur->_data){cur_parent = cur;cur = cur->_left;}else{return false;}}//找到空位后,给空位一个新结点cur = new Node(tmp);if (cur->_data > cur_parent->_data){cur_parent->_right = cur;cur->_parent = cur_parent;}else{cur_parent->_left = cur;cur->_parent = cur_parent;}②更新平衡因子
插入完结点后, 我们要更新平衡因子,那么怎么更新呢,我们往下看。
首先,当插入一个新结点的时候,只会影响新结点一路往上的_parent结点。如下图所示。
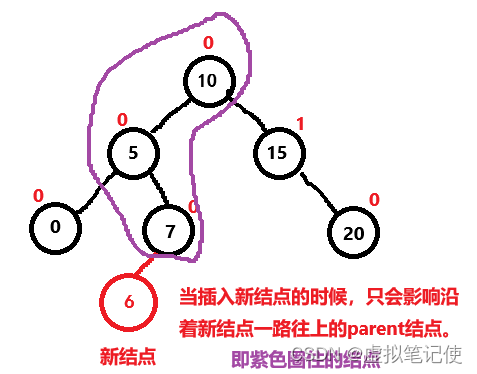
所以当我们更新平衡因子的时候,只需要通过_parent指针,一路向上更新即可,但是也不一定一直更新到根节点,为什么呢?我继续往下看。
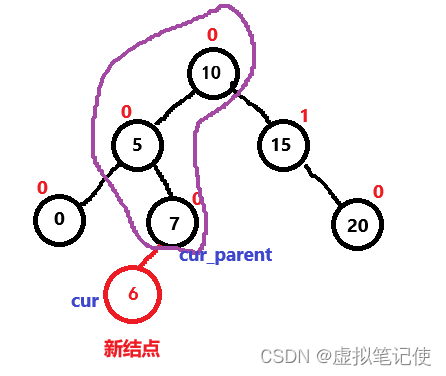
既然是更新平衡因子,那么怎么个更新呢?
在开头,我们提到_bf平衡因子 = 右子树的高度 - 左子树的高度。
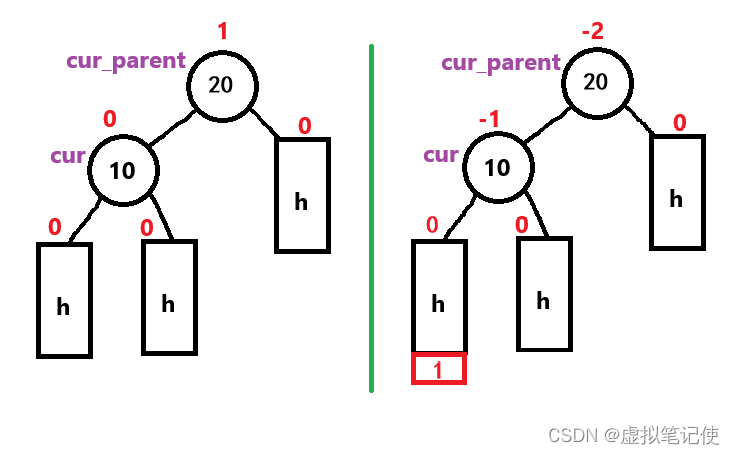
那么看上图,cur为新结点,cur_parent为cur的父结点,对于cur_parent来说,它的左子树新增了一个结点,也就是说左子树的高度+1,所以对于_bf = 右子树高度 - 左子树高度这个公式来说,左子树高度+1,即_bf-1,如果cur是cur_parent的右子树反之+1。这里可能会很乱,没事,我们来看下图。

当更新完一个结点的平衡因子的时候,这个时候会有三种情况:
1.更新完该结点后,会影响向上的父结点,继续更新。
2.更新完该结点后,不会影响向上的父结点,更新结束。
3.更新完该结点后,该结点的平衡因子==2或==-2,此时需要进行旋转处理。
整个过程的代码如下。
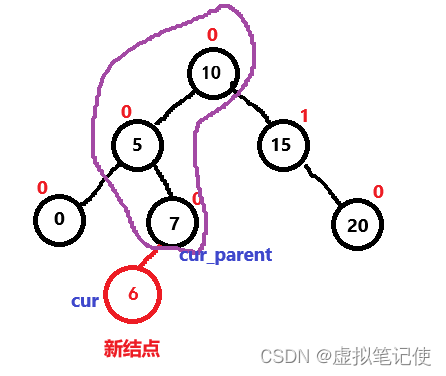
//插入完结点后,要更新平衡因子while (cur_parent != nullptr){if (cur_parent->_right == cur)//说明新增结点是cur_parent的右子树,即右子树高度增加1{cur_parent->_bf++;}else{cur_parent->_bf--;}if (cur_parent->_bf == 0)//如果cur_parent的平衡因子为0,结束更新{break;}else if (cur_parent->_bf == 1 || cur_parent-> == -1)//如果cur_parent的平衡因子为1或者-1,则继续向上更新{cur = cur_parent;cur_parent = cur_parent->_parent;}else if (cur_parent->_bf == 2 || cur_parent->_bf == -2){//进行旋转处理}更新平衡因子情况分析
更新完后,为什么平衡因子==0就停止更新,==1或者==-1要继续向上更新?
我们来分析一下。首先来看==0情况。如下图所示
我们插入20,插入后结点15的平衡因子要更新为0,
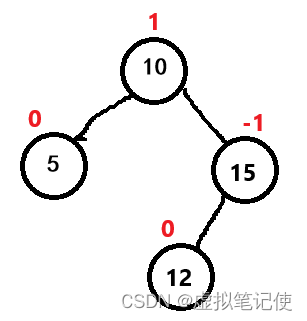
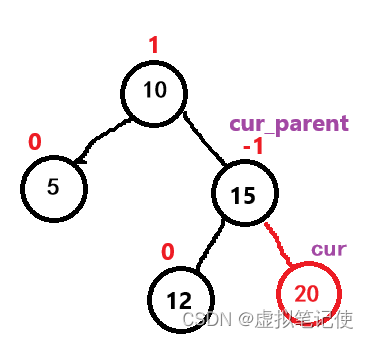
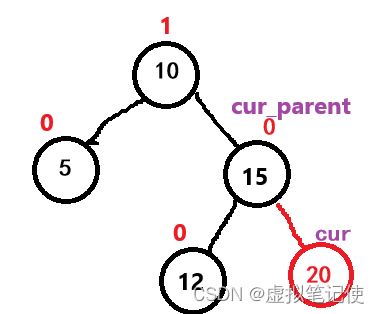
从图中,我们可以轻易的看出对于结点10来说,它的平衡因子是不受影响的,那么是为什么呢?
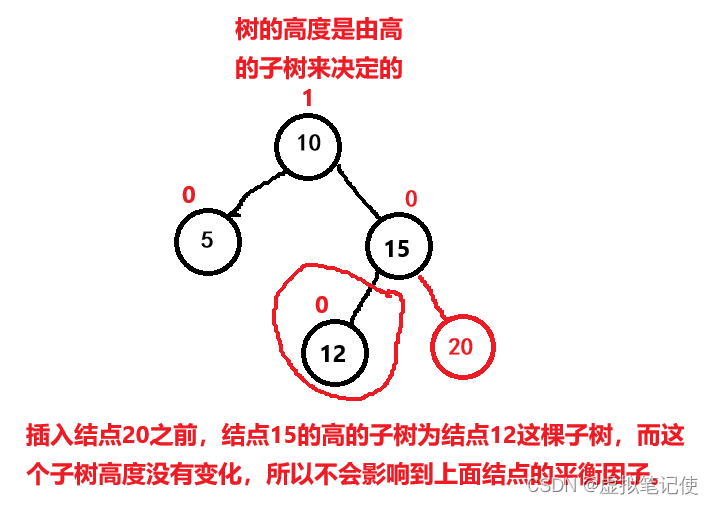
因为树的高度是由高的子树来决定的,对于结点10来说,它的高的子树是(15~12)这个两个结点构成的子树,而新增的结点20没有增加到高的子树上去,所以对于结点10来说,高度没变。如下图所示。
接下来看看==1或者==-1的情况,
首先是一棵正常的树,我们插入新结点20,插入后,结点18的平衡因子要变为1,

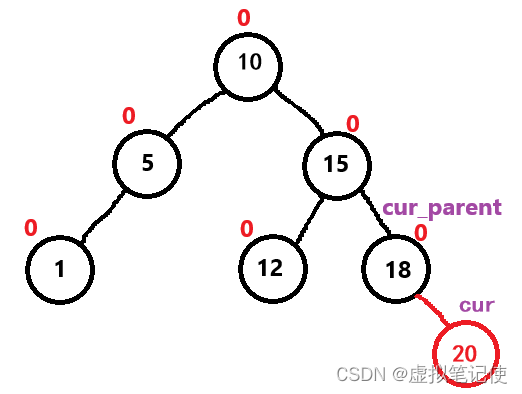
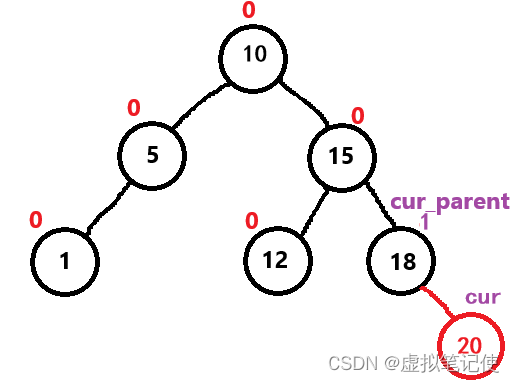
因为结点18的平衡因子为1,所以要继续向上更新,为什么呢?
解释与上面那种情况类似,当一个结点的平衡因子由0变为1或者-1的时候,说明该结点的高度增加了1,说明该结点的子树高度增加了1,这个时候会影响上面结点的高度,所以平衡因子要一直向上更新。
③判断是否要旋转
至于当平衡因子==2或者==-2的时候,要进行旋转处理就没什么好说的了,因为AVLTree就是严格的要求平衡因子的绝对值不能大于2。
那么旋转又是怎么旋转的呢?
旋转又可以分为四种情况:左单旋,右单旋,左右双旋,右左双旋。
我们来分析一下。
左单旋
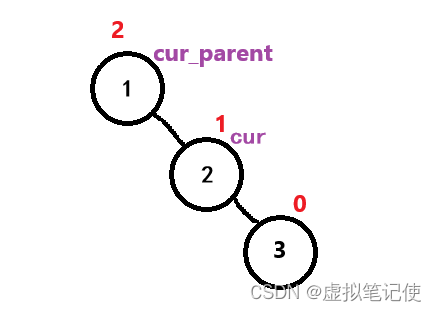
当一个结点的_bf为2,且它的右孩子的_bf为1时,要进行左单旋。 如下图所示
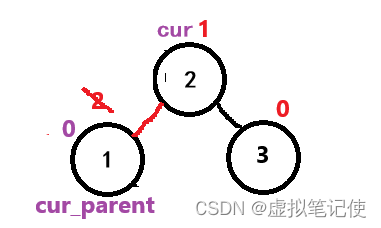
旋转完后,如下图所示。
对于左单旋的所有情况,我们可以用下面这两个抽象图来表示所有情况。
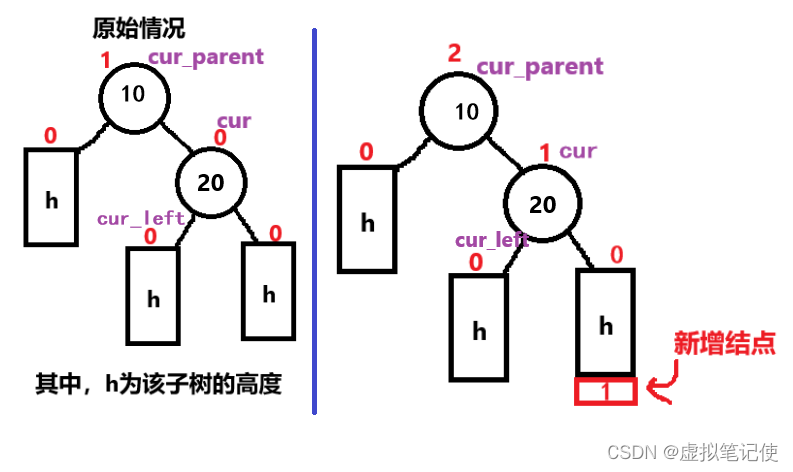
进行旋转处理后,如下图所示。
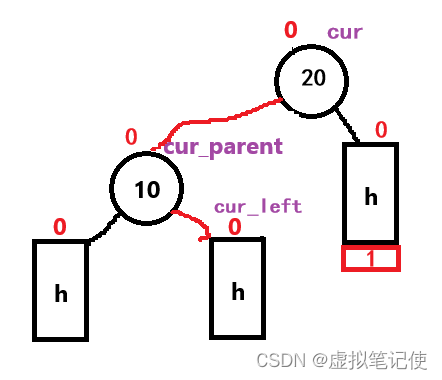
对于整个旋转过程来说,就是去改变cur_parent和cur结点的指针关系。
cur_parent的右指针,去指向cur的左子树,
cur的左指针,去指向cur_parent,
注意,这里还要改变cur_parent和cur结点的_parent指针。
但是这里注意的时,cur_parent不一定如上图所示为根结点,它有可能是某个结点的子树,如下图所示。
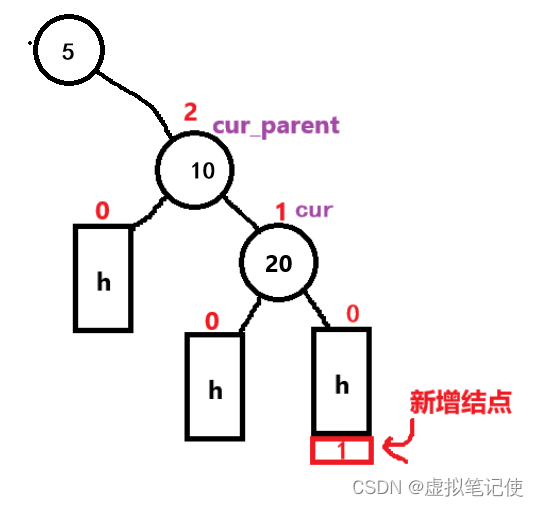
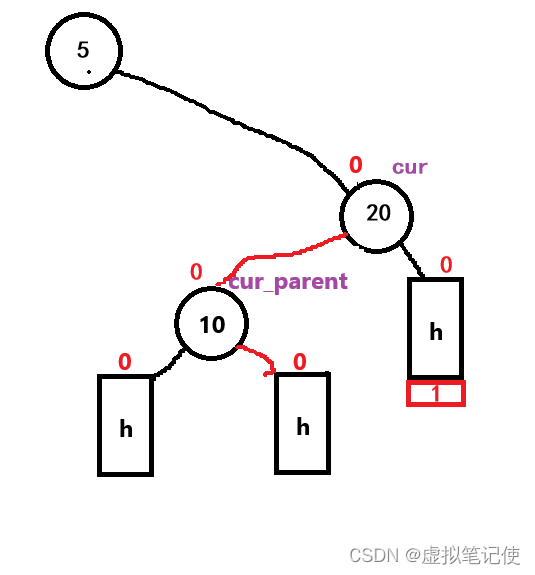
所以旋转完成后还要进行一次判断,是否需要将cur结点链接到上一个结点。
//左单旋 void RotateL(Node* cur_parent){Node* cur = cur_parent->_right;Node* cur_left = cur->_left;//改变指针的链接关系cur_parent->_right = cur_left;if (cur_left != nullptr){cur_left->_parent = cur_parent;}cur->_left = cur_parent;Node* cur_parent_parent = cur_parent->_parent;//提前保存cur_parent的父结点cur_parent->_parent = cur;//旋转完成后要判断cur_parent是否为根if (cur_parent_parent != nullptr)//说明cur_parent不是根{if (cur_parent_parent->_data < cur_parent->_data){cur_parent_parent->_right = cur;cur->_parent = cur_parent_parent;}else{cur_parent_parent->_left = cur;cur->_parent = cur_parent_parent;}}else//说明cur_parent是根{_root = cur;cur->_parent = nullptr;}//旋转完成后,平衡因子调整为0cur_parent->_bf = cur->_bf = 0;}右单旋
同样的右单旋与左单旋类似,只不过是反过来而已,这里不再做过多的解释,只给出抽象图出来。
经过右单旋后,变成如下图所示。
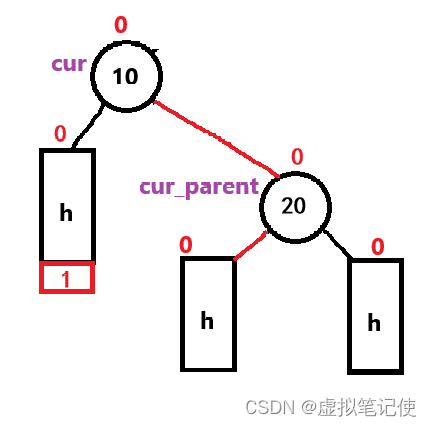
//右单旋void RotateR(Node* cur_parent){Node* cur = cur_parent->_left;Node* cur_right = cur->_right;cur_parent->_left = cur_right;if (cur_right != nullptr){cur_right->_parent = cur_parent;}cur->_right = cur_parent;Node* cur_parent_parent = cur_parent->_parent;cur_parent->_parent = cur;if (cur_parent_parent != nullptr){if (cur_parent_parent->_data > cur_parent->_data){cur_parent_parent->_left = cur;cur->_parent = cur_parent_parent;}else{cur_parent_parent->_right = cur;cur->_parent = cur_parent_parent;}}else{_root = cur;cur->_parent = nullptr;}cur_parent->_bf = cur->_bf = 0;}左右单旋
左单旋和右单旋解释完成后,接下来要将双旋了,那么什么情况下要用双旋呢?
我们来看一下抽象图
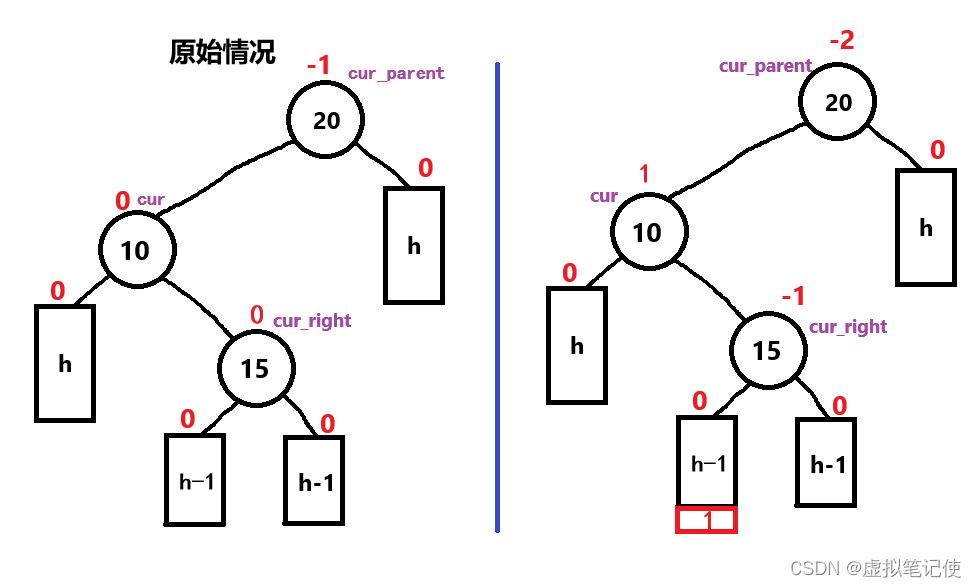
当新插入结点时,如果符合上图中的情况,则要进行左右双旋操作,注意!!!新增的红色结点也有可能插入在结点15的右树,其旋转过程就是先对结点10进行一个左单旋,再对结点20进行一个右单旋。如下图所示。
先对结点10进行一个左单旋,再对结点20进行一个右单旋。
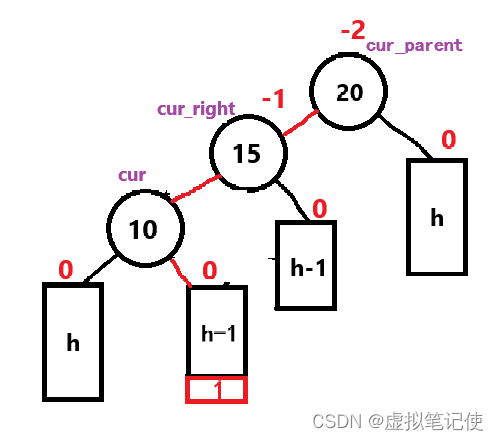
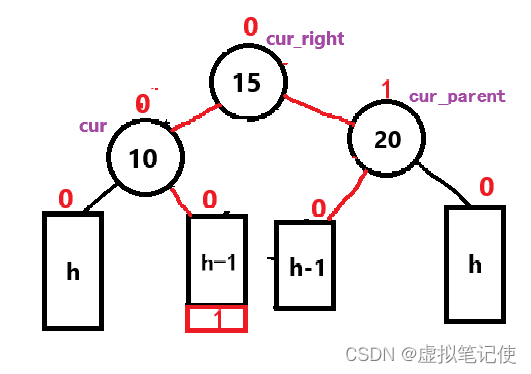
但是上面这个抽象图不能代表双旋的所有情况,因为双旋有一种特殊的情况,如下图所示。
对于这种特殊情况,我们只需要先前保存cur_right的平衡因子,双旋完成后,如果平衡因子为0,说明就是这种特殊情况,再进行特殊处理即可。
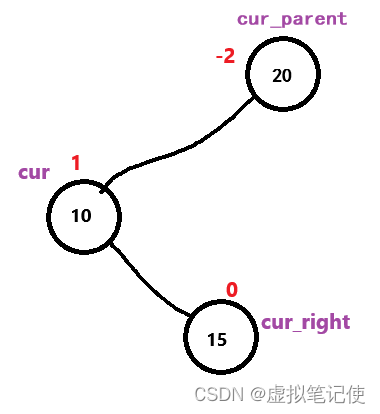
//左右双旋void RotateLR(Node* cur_parent){Node* cur = cur_parent->_left;Node* cur_right = cur->_right;int bf = cur_right->_bf;//这里保存平衡因子的原因是,新增的结点有可能插入在左树,也有可能插入在右树,通过保存平衡因子来进行判断是哪一种情况//先对cur进行一个左单旋RotateL(cur);//再对cur_parent进行一个右单旋RotateR(cur_parent);//旋转完成后,要更新平衡因子if (bf == -1)//说明新增的结点是插入在左树{cur->_bf = 0;cur_parent->_bf = 1;cur_right->_bf = 0;}else if (bf == 1)//说明新增的结点是插入在右树{cur->_bf = -1;cur_parent->_bf = 0;cur_right->_bf = 0;}else if (bf == 0)//特殊情况{cur->_bf = 0;cur_parent->_bf = 0;cur_right->_bf = 0;}}右左双旋
对于右左双旋来说,与左右单旋类似,就是换了个方向而已,这里不再过多的解释,直接给出抽象图和代码。
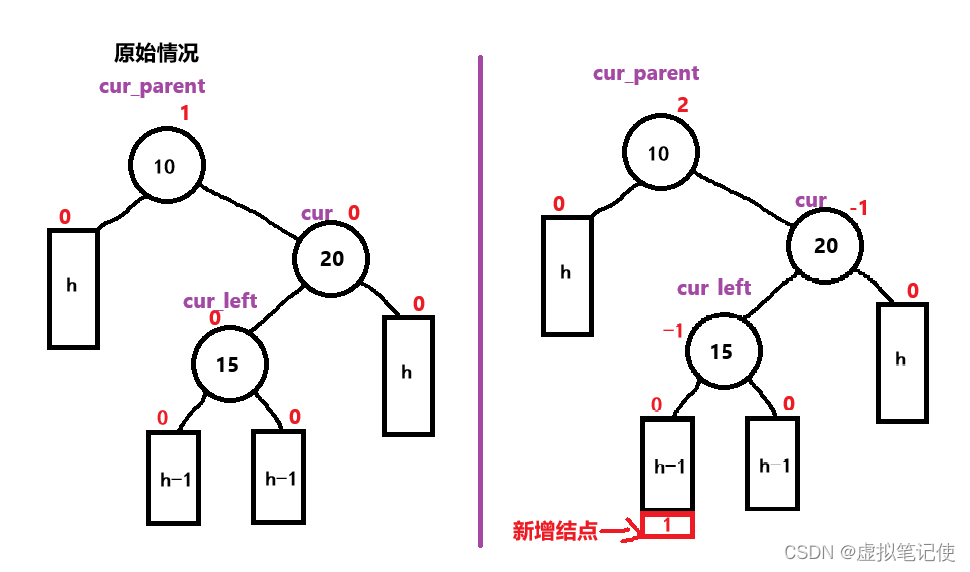
先进行一个右单旋,再进行一个左单旋,旋转如下图所示。
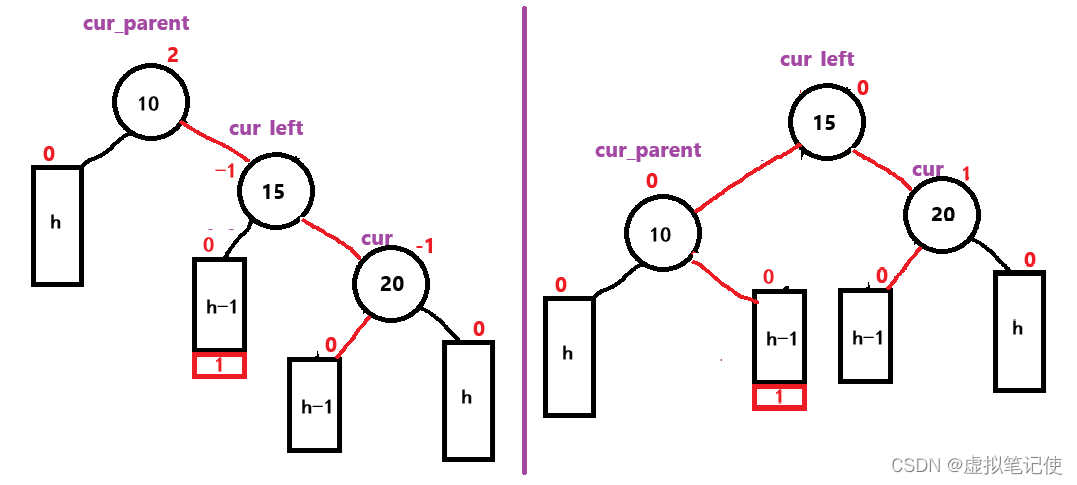
同样的,这里也要处理特殊情况,就不在过多的解释。
//右左双旋void RotateRL(Node* cur_parent){Node* cur = cur_parent->_right;Node* cur_left = cur->_left;int bf = cur_left->_bf;//先对cur进行一个右单旋RotateR(cur);//再对cur_parent进行一个左单旋RotateL(cur_parent);//更新平衡因子if (bf == -1){cur->_bf = 1;cur_parent->_bf = 0;cur_left->_bf = 0;}else if (bf == 1){cur->_bf = 0;cur_parent->_bf = -1;cur_left->_bf = 0;}else if (bf == 0){cur->_bf = 0;cur_parent->_bf = 0;cur_left->_bf = 0;}}走到这一步,我们的旋转代码就已经全部写好了,接下来可以接着补充我们的插入函数的旋转部分。
bool insert(const T& tmp){//如果根节点为空,则直接插入if (_root == nullptr){_root = new Node(tmp);return true;}//如果根节点不为空,则先按二叉搜索树的规则进行插入Node* cur = _root;Node* cur_parent = nullptr;while (cur != nullptr)//往下找空位{if (tmp > cur->_data){cur_parent = cur;cur = cur->_right;}else if (tmp < cur->_data){cur_parent = cur;cur = cur->_left;}else{return false;}}//找到空位后,给空位一个新结点cur = new Node(tmp);if (cur->_data > cur_parent->_data){cur_parent->_right = cur;cur->_parent = cur_parent;}else{cur_parent->_left = cur;cur->_parent = cur_parent;}//插入完结点后,要更新平衡因子while (cur_parent != nullptr){if (cur_parent->_right == cur){cur_parent->_bf++;}else{cur_parent->_bf--;}if (cur_parent->_bf == 0){break;}else if (cur_parent->_bf == 1 || cur_parent->_bf == -1){cur = cur_parent;cur_parent = cur_parent->_parent;}else if (cur_parent->_bf == 2 || cur_parent->_bf == -2){//进行旋转处理if (cur_parent->_bf == 2){if (cur->_bf == 1)//左单旋{RotateL(cur_parent);}else if(cur->_bf == -1)//右左双旋{RotateRL(cur_parent);}}else if (cur_parent->_bf == -2){if (cur->_bf == 1)//左右单旋{RotateLR(cur_parent);}else if (cur->_bf == -1)//右单旋{RotateR(cur_parent);}}break;}}return true;}写到这里,我们的插入代码就完成了,这也是AVLTree实现的最核心的部分。
4.删除、查找和修改函数
对于一个数据结构来说,最基本的操作是增删改查,现在增已经实现了,那么还有剩下的三个函数。
删除:
对于AVLTree的删除来说,情况比插入还稍许复杂,又由于博主的能力和精力有限,在这里就不讲了。
查找:
对于AVLTree的查找来说,就显得很简单,跟二叉搜索树的查找一样,就不过多的解释,等下下面直接给出代码。
修改:
对于AVLTree的修改来说,一般来说,是不允许修改的,因为AVLTree是一种搜索树,它的中序遍历是绝对的有序的,如果进行修改,就会破坏整棵树的性质,导致不再是搜索树,但是也有允许修改的情况,当树中存的是一个pair键值对,我们可以对pair键值对的val进行修改,具体解释,参考这篇博客中的kv模型【C++】二叉搜索树-CSDN博客
查找结点
//查找结点Node* find(const T& tmp){Node* cur = _root;while (cur != nullptr){if (tmp > cur->_data){cur = cur->_right;}else if (tmp < cur->_data){cur = cur->_left;}else{return cur;}}return nullptr;}三.测试
既然我们的插入已经完成了,那么我们又如何判断我们写的代码是对的呢,接下来讲一下如何测试我们写的AVLTree。
1.判断是否是搜索树
既然是AVLTree,那么它一定是一棵搜索树,所以它的中序遍历一定是有序的,所以我们可以写一个中序遍历来看看是否是搜索树。
//中序遍历void InOrder(){Node* cur = _root;_InOrder(cur);}//中序遍历的子函数void _InOrder(Node* cur){if (cur == nullptr)return;_InOrder(cur->_left);cout << cur->_data << " ";_InOrder(cur->_right);}2.判断每一个结点的左右子树高度差是否不大于1
判断完了确定是搜索树,接下来就要判断是否是AVLTree树,即每一个结点的左右子树高度差都不大于1。
首先,我们可以先写一个求树的高度的函数。
//求树的高度int height(Node* cur){if (cur == nullptr)return 0;//返回左右子树高的那一个子树+1,fmax是库函数,求两个参数的较大值return fmax(height(cur->_left), height(cur->_right)) + 1;}然后就可以写一个判断是否平衡的函数。
//判断是否平衡bool JudgeBanlance(){Node* cur = _root;return _JudgeBanlance(cur);}//判断是否平衡的子函数bool _JudgeBanlance(Node* cur){if (cur == nullptr)return true;int left_height = height(cur->_left);//求cur左子树的高度int right_height = height(cur->_right);//求cur右子树的高度//abs是求左右子树高度差的绝对值return abs(left_height - right_height) < 2&& _JudgeBanlance(cur->_left)&& _JudgeBanlance(cur->_right);}写到这里,我们的判断是否是AVLTree也完成了,AVLTree也基本实现了。
四.所有源代码
AVLTree.h
#pragma once
#include<iostream>
#include<time.h>
using namespace std;
//编写一篇博客
namespace blog_AVLTree
{template<class T>struct TreeNode{//成员变量T _data;//树结点存储的数据类型TreeNode<T>* _left;//左孩子指针TreeNode<T>* _right;//右孩子指针TreeNode<T>* _parent;//父结点指针int _bf;//平衡因子//成员函数TreeNode(const T& tmp)//构造函数:_data(tmp), _left(nullptr), _right(nullptr), _parent(nullptr), _bf(0){}};template<class T>class AVLTree{typedef TreeNode<T> Node;public:AVLTree():_root(nullptr){}//插入bool insert(const T& tmp){//如果根节点为空,则直接插入if (_root == nullptr){_root = new Node(tmp);return true;}//如果根节点不为空,则先按二叉搜索树的规则进行插入Node* cur = _root;Node* cur_parent = nullptr;while (cur != nullptr)//往下找空位{if (tmp > cur->_data){cur_parent = cur;cur = cur->_right;}else if (tmp < cur->_data){cur_parent = cur;cur = cur->_left;}else{return false;}}//找到空位后,给空位一个新结点cur = new Node(tmp);if (cur->_data > cur_parent->_data){cur_parent->_right = cur;cur->_parent = cur_parent;}else{cur_parent->_left = cur;cur->_parent = cur_parent;}//插入完结点后,要更新平衡因子while (cur_parent != nullptr){if (cur_parent->_right == cur){cur_parent->_bf++;}else{cur_parent->_bf--;}if (cur_parent->_bf == 0){break;}else if (cur_parent->_bf == 1 || cur_parent->_bf == -1){cur = cur_parent;cur_parent = cur_parent->_parent;}else if (cur_parent->_bf == 2 || cur_parent->_bf == -2){//进行旋转处理if (cur_parent->_bf == 2){if (cur->_bf == 1)//左单旋{RotateL(cur_parent);}else if(cur->_bf == -1)//右左双旋{RotateRL(cur_parent);}}else if (cur_parent->_bf == -2){if (cur->_bf == 1)//左右单旋{RotateLR(cur_parent);}else if (cur->_bf == -1)//右单旋{RotateR(cur_parent);}}break;}}return true;}//查找结点Node* find(const T& tmp){Node* cur = _root;while (cur != nullptr){if (tmp > cur->_data){cur = cur->_right;}else if (tmp < cur->_data){cur = cur->_left;}else{return cur;}}return nullptr;}//中序遍历void InOrder(){Node* cur = _root;_InOrder(cur);}//求树的高度int height(Node* cur){if (cur == nullptr)return 0;return fmax(height(cur->_left), height(cur->_right)) + 1;}//判断是否平衡bool JudgeBanlance(){Node* cur = _root;return _JudgeBanlance(cur);}private://左单旋 void RotateL(Node* cur_parent){Node* cur = cur_parent->_right;Node* cur_left = cur->_left;//改变指针的链接关系cur_parent->_right = cur_left;if (cur_left != nullptr){cur_left->_parent = cur_parent;}cur->_left = cur_parent;Node* cur_parent_parent = cur_parent->_parent;cur_parent->_parent = cur;//旋转完成后要判断cur_parent是否为根if (cur_parent_parent != nullptr)//说明cur_parent不是根{if (cur_parent_parent->_data < cur_parent->_data){cur_parent_parent->_right = cur;cur->_parent = cur_parent_parent;}else{cur_parent_parent->_left = cur;cur->_parent = cur_parent_parent;}}else//说明cur_parent是根{_root = cur;cur->_parent = nullptr;}//旋转完成后,平衡因子调整为0cur_parent->_bf = cur->_bf = 0;}//右单旋void RotateR(Node* cur_parent){Node* cur = cur_parent->_left;Node* cur_right = cur->_right;cur_parent->_left = cur_right;if (cur_right != nullptr){cur_right->_parent = cur_parent;}cur->_right = cur_parent;Node* cur_parent_parent = cur_parent->_parent;cur_parent->_parent = cur;if (cur_parent_parent != nullptr){if (cur_parent_parent->_data > cur_parent->_data){cur_parent_parent->_left = cur;cur->_parent = cur_parent_parent;}else{cur_parent_parent->_right = cur;cur->_parent = cur_parent_parent;}}else{_root = cur;cur->_parent = nullptr;}cur_parent->_bf = cur->_bf = 0;}//左右双旋void RotateLR(Node* cur_parent){Node* cur = cur_parent->_left;Node* cur_right = cur->_right;int bf = cur_right->_bf;//先对cur进行一个左单旋RotateL(cur);//再对cur_parent进行一个右单旋RotateR(cur_parent);//旋转完成后,要更新平衡因子if (bf == -1){cur->_bf = 0;cur_parent->_bf = 1;cur_right->_bf = 0;}else if (bf == 1){cur->_bf = -1;cur_parent->_bf = 0;cur_right->_bf = 0;}else if (bf == 0)//特殊情况{cur->_bf = 0;cur_parent->_bf = 0;cur_right->_bf = 0;}}//右左双旋void RotateRL(Node* cur_parent){Node* cur = cur_parent->_right;Node* cur_left = cur->_left;int bf = cur_left->_bf;//先对cur进行一个右单旋RotateR(cur);//再对cur_parent进行一个左单旋RotateL(cur_parent);//更新平衡因子if (bf == -1){cur->_bf = 1;cur_parent->_bf = 0;cur_left->_bf = 0;}else if (bf == 1){cur->_bf = 0;cur_parent->_bf = -1;cur_left->_bf = 0;}else if (bf == 0){cur->_bf = 0;cur_parent->_bf = 0;cur_left->_bf = 0;}}//中序遍历的子函数void _InOrder(Node* cur){if (cur == nullptr)return;_InOrder(cur->_left);cout << cur->_data << " ";_InOrder(cur->_right);}//判断是否平衡的子函数bool _JudgeBanlance(Node* cur){if (cur == nullptr)return true;int left_height = height(cur->_left);//求cur左子树的高度int right_height = height(cur->_right);//求cur右子树的高度return abs(left_height - right_height) < 2&& _JudgeBanlance(cur->_left)&& _JudgeBanlance(cur->_right);}private:Node* _root;};void Test1(){AVLTree<int> root;//int arr[] = { 16, 3, 7, 11, 9, 26, 18, 14, 15 };int arr[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++){root.insert(arr[i]);}root.InOrder();cout << root.JudgeBanlance() << endl;}void Test2(){srand(time(0));AVLTree<int> root;const int n = 100;for (int i = 0; i < n; i++){root.insert(rand());}root.InOrder();cout << root.JudgeBanlance() << endl;}
}Test.c
#include"AVLTree.h"int main()
{blog_AVLTree::Test1();//blog_AVLTree::Test2();return 0;
}相关文章:

【数据结构】AVLTree实现详解
目录 一.什么是AVLTree 二.AVLTree的实现 1.树结点的定义 2.类的定义 3.插入结点 ①按二叉搜索树规则插入结点 ②更新平衡因子 更新平衡因子情况分析 ③判断是否要旋转 左单旋 右单旋 左右单旋 右左双旋 4.删除、查找和修改函数 查找结点 三.测试 1.判断是否是搜索树 …...
深度学习——TensorBoard的使用
官方文档torch.utils.tensorboard — PyTorch 2.3 documentation TensorBoard简介 TensorBoard是一个可视化工具,它可以用来展示网络图、张量的指标变化、张量的分布情况等。特别是在训练网络的时候,我们可以设置不同的参数(比如࿱…...
⭐⭐⭐)
【设计模式】观察者模式(行为型)⭐⭐⭐
文章目录 1.概念1.1 什么是观察者模式1.2 优点与缺点 2.实现方式3. Java 哪些地方用到了观察者模式4. Spring 哪些地方用到了观察者模式 1.概念 1.1 什么是观察者模式 观察者模式(Observer Pattern)是一种行为型设计模式,它允许对象在状态改…...

轻松搞定阿里云域名DNS解析
本文将会讲解如何设置阿里云域名DNS解析。在进行解析设置之前,你需要提前准备好需要设置的云服务器IP地址、域名以及CNAME记录。 如果你还没有云服务器和域名,可以参考下面的方法注册一个。 申请域名:《Namesilo域名注册》注册云服务器&…...

GAT1399协议分析(10)--单图像删除
一、官方接口 由于批量删除的接口,图像只能单独删除。 二、wireshark实例 这个接口比较简单,调用request delete即可 文本化: DELETE /VIID/Images/34078100001190001002012024060513561300065 HTTP/1.1 Host: 10.0.201.56:31400 User-Age…...

Hudi CLI 安装配置总结
前言 上篇文章 总结了Spark SQL Rollback, Hudi CLI 也能实现 Rollback,本文总结下 Hudi CLI 安装配置以及遇到的问题。 官方文档 https://hudi.apache.org/cn/docs/cli/ 版本 Hudi 0.13.0(发现有bug)、(然后升级)0.14.1Spark 3.2.3打包 mvn clean package -DskipTes…...
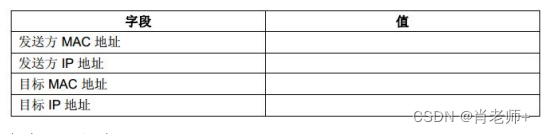
实验八、地址解析协议《计算机网络》
水逆退散,学业进步,祝我们都好,不止在夏天。 目录 一、实验目的 二、实验内容 (1)预备知识 (2)实验步骤 三、实验小结 一、实验目的 完成本练习之后,您应该能够确定给定 IP 地…...

Linux系统管理磁盘管理003
操作系统: CentOS Stream9 测试过程: 模拟磁盘被沾满, 创建文件 测试脚本 for i in seq 10do# echo $idd if/dev/zero of./$i-$RANDOM.txt bs1M count1024 Done[rootlocalhost ~]# vim 2.txt [rootlocalhost ~]# sh 2.txt 记录了10240 的…...

MLC工具是否适用AMD和ARM场景?如何测试内存性能?
MLC(Memory Latency Checker)主要是由Intel开发的工具,主要用于Intel平台上的内存性能测试,尤其是针对Intel处理器的内存延迟和带宽。尽管MLC主要针对Intel处理器设计,理论上它可以在任何支持Intel兼容指令集的系统上运…...

NodeJs实现脚本:将xlxs文件输出到json文件中
文章目录 前期工作和依赖笔记功能代码输出 最近有一个功能,将json文件里的内容抽取到一个xlxs中,然后维护xlxs文件。当要更新json文件时,就更新xlxs的内容并把它传回json中。这个脚本主要使用NodeJS写。 以下是完成此功能时做的一些笔记。 …...

【启程Golang之旅】网络编程与反射
欢迎来到Golang的世界!在当今快节奏的软件开发领域,选择一种高效、简洁的编程语言至关重要。而在这方面,Golang(又称Go)无疑是一个备受瞩目的选择。在本文中,带领您探索Golang的世界,一步步地了…...

nginx location正则表达式+案例解析
1、nginx常用的正则表达式 ^ :匹配输入字符串的起始位置$ :匹配输入字符串的结束位置 *:匹配前面的字符零次或多次。如“ol*”能匹配“o”及“ol”、“oll” :匹配前面的字符一次或多次。如“ol”能匹配“ol”及“oll”、“olll”…...

【YOLO系列】YOLOv10论文超详细解读(翻译 +学习笔记)
前言 研究AI的同学们面对的一个普遍痛点是,刚开始深入研究一项新技术,没等明白透彻,就又迎来了新的更新版本——就像我还在忙着逐行分析2月份发布的YOLOv9代码,5月底清华的大佬们就推出了全新的v10。。。 在繁忙之余࿰…...
植物大战僵尸杂交版2024潜艇伟伟迷
在广受欢迎的游戏《植物大战僵尸》的基础上,我最近设计了一款创新的杂交版游戏,简直是太赞了!这款游戏结合了原有游戏的塔防机制,同时引入新的元素、角色和挑战,为玩家提供了全新的游戏体验。 植物大战僵尸杂交版最新绿…...

白话解读网络爬虫
网络爬虫(Web Crawler),也称为网络蜘蛛、网络机器人或网络蠕虫,是一种自动化程序或脚本,被用来浏览互联网并收集信息。网络爬虫的主要功能是在互联网上自动地浏览网页、抓取内容并将其存储在本地或远程服务器上供后续处…...
: 从理论到实践的指南(1))
支持向量机(SVM): 从理论到实践的指南(1)
支持向量机(SVM)被誉为数据科学领域的重量级算法,是机器学习中不可或缺的工具之一。SVM以其优秀的泛化能力和对高维数据的管理而备受推崇。本文旨在梳理SVM的核心概念以及其在实际场景中的应用。 SVM的核心理念 SVM专注于为二分类问题找到最…...

万字长文|OpenAI模型规范(全文)
本文是继《OpenAI模型规范概览》之后对OpenAI Model Spec的详细描述,希望能对各位从事大模型及RLHF研究的朋友有帮助。万字长文,建议收藏后阅读。 一、概述 在AI的世界里,确保技术的行为符合我们的期望至关重要。OpenAI最近发布了一份名为Mo…...
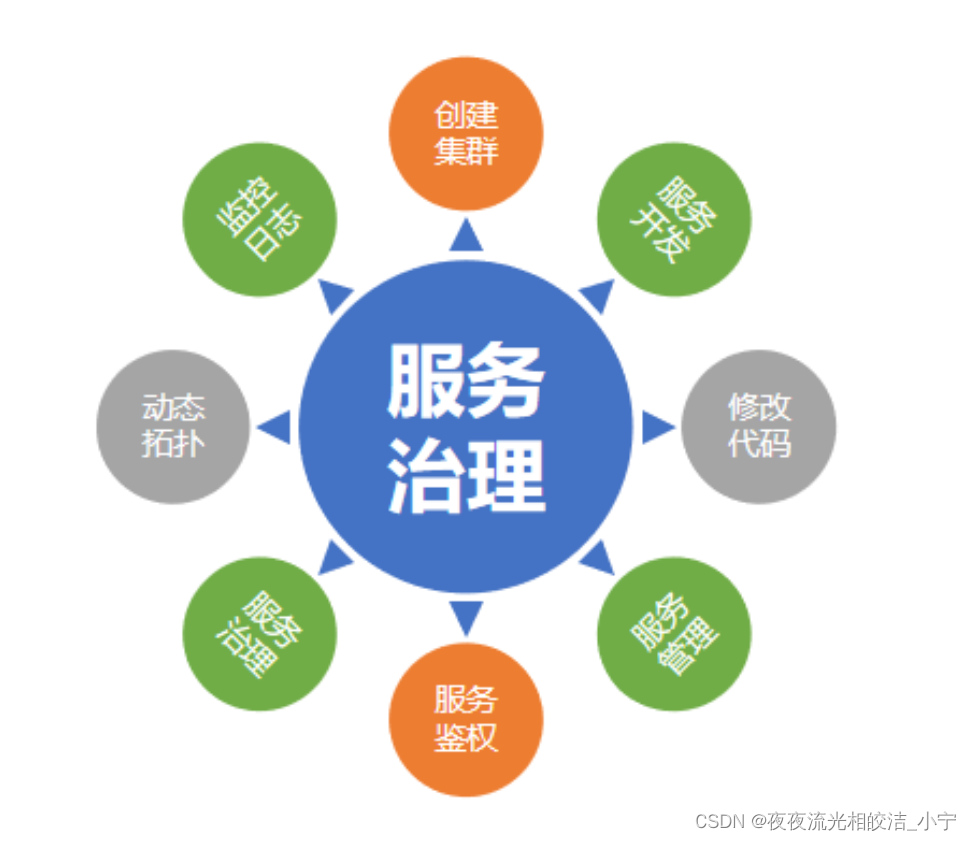
微服务架构-正向治理与治理效果
目录 一、正向治理 1.1 概述 1.2 效率治理 1.2.1 概述 1.2.2 基于流量录制和回放的测试 1.2.3 基于仿真环境的测试 1.3 稳定性治理 1.3.1 概述 1.3.2 稳定性治理模型 1.3.3 基于容器化的稳定性治理 1.3.3.1 概述 1.3.3.2 测试 1.3.3.3 部署 1.3.3.3.1 概述 1.3.3…...

normalizing flows vs 直方图规定化
normalizing flows名字的由来 The base density P ( z ) P(z) P(z) is usually defined as a multivariate standard normal (i.e., with mean zero and identity covariance). Hence, the effect of each subsequent inverse layer is to gradually move or “flow” the da…...
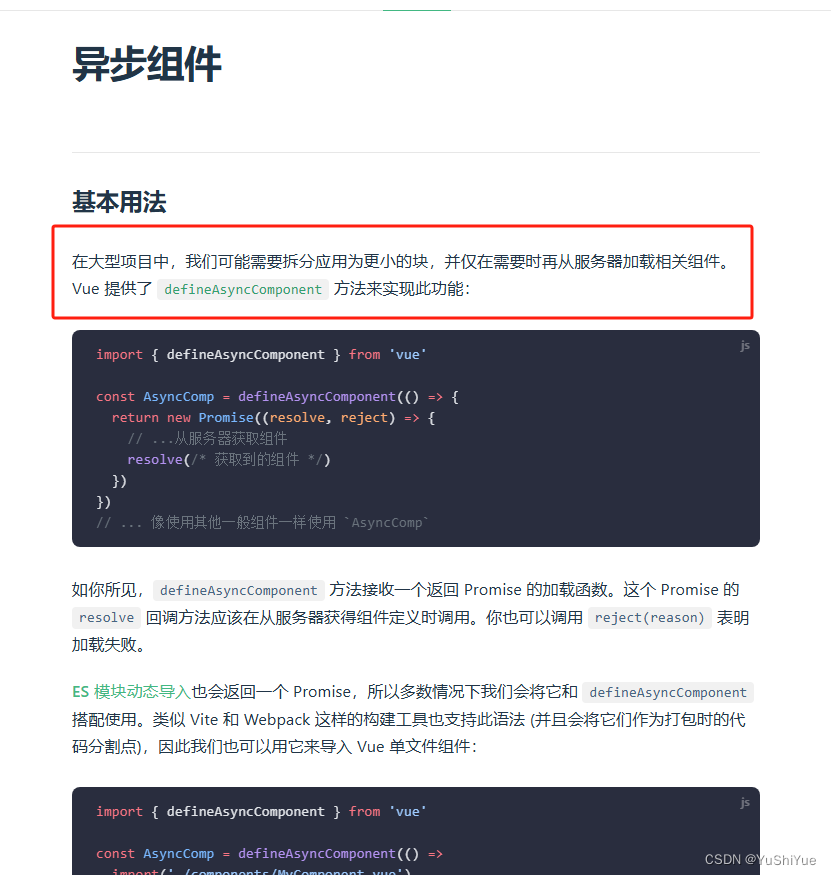
vite打包优化常用的技巧及思路
面试题:vitevue项目如何进行优化? 什么情况下会去做打包优化?一种是在搭建项目的时候就根据自己的经验把vite相关配置给处理好,另外一种是开发的过程中发现打包出来的静态资源越来越大,导致用户访问的时候资源加载慢&a…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

WordPress插件:AI多语言写作与智能配图、免费AI模型、SEO文章生成
厌倦手动写WordPress文章?AI自动生成,效率提升10倍! 支持多语言、自动配图、定时发布,让内容创作更轻松! AI内容生成 → 不想每天写文章?AI一键生成高质量内容!多语言支持 → 跨境电商必备&am…...

OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别
OpenPrompt 和直接对提示词的嵌入向量进行训练有什么区别 直接训练提示词嵌入向量的核心区别 您提到的代码: prompt_embedding = initial_embedding.clone().requires_grad_(True) optimizer = torch.optim.Adam([prompt_embedding...

爬虫基础学习day2
# 爬虫设计领域 工商:企查查、天眼查短视频:抖音、快手、西瓜 ---> 飞瓜电商:京东、淘宝、聚美优品、亚马逊 ---> 分析店铺经营决策标题、排名航空:抓取所有航空公司价格 ---> 去哪儿自媒体:采集自媒体数据进…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...
