【论文阅读】MODELING AND SOLVING THE TRAVELING SALESMAN PROBLEM WITH PRIORITY PRIZES
文章目录
- 论文基本信息
- 摘要
- 1.引言
- 2. INTEGER QUADRATIC PROGRAM FOR TSPPP
- 3. MIXED INTEGER LINEAR PROGRAMS FOR TSPPP
- 4. TABU SEARCH ALGORITHM FOR TSPPP
- 5. COMPUTATIONAL RESULTS
- 6. CONCLUDING REMARKS
- 补充
论文基本信息
《MODELING AND SOLVING THE TRAVELING SALESMAN PROBLEM WITH PRIORITY PRIZES》
摘要
本文研究了具有优先奖励(TSPPP)的旅行商问题,这是经典TSP的扩展,在目标函数中考虑了节点访问的顺序。当节点i以路线的第k个顺序访问时,旅行销售员收到奖励pki,而当销售员从节点i旅行到节点j时,产生旅行成本cij。TSPPP的目的是找到最大利润的n-节点之旅。这个问题可以被看作是一个具有更一般的目标函数的TSP变体,旨在针对在某种程度上考虑客户服务质量、交付优先级和成本的解决方案。在这里,TSPPP的一个自然表示是基于库普曼斯和贝克曼方法的观点,根据这个观点,这个问题似乎是二次分配问题(QAP)的一个特殊情况。鉴于这种TSP变体的新颖性,我们提出了不同的混合整数规划模型来适当地表示TSPPP,其中一些模型是基于QAP的。利用著名的优化软件和塔卡搜索算法求解MIP模型时,还进行了计算实验。
1.引言
旅行推销员问题(TSP)是网络优化中研究最广泛的问题之一,对[2,5,20,24]具有广泛的实际应用。问题在于定义一个从仓库访问客户的最佳旅行,自从Dantzig和合作者[7,8]的开创性工作以来,已经提出了几种模型和方法来有效地表示和解决大型问题实例。TSP的许多变体已经在文献中被研究过,而开创性的数学规划模型往往是大多数这些变体[4,11,22,28]的基础。
旅行推销员优先奖励问题(TSPPP)是经典TSP的扩展,其中所有的客户(节点)都必须由旅行推销员访问,并在目标函数中直接考虑客户访问的顺序。如果客户i按第k次顺序访问,旅行推销员将获得奖励pki,而从客户i旅行到客户j将产生旅行费用cij。请注意,pki可以包括旅行销售员在访问节点i时获得的奖品,独立于我访问的顺序k,以及他/她在路线的k顺序访问节点i时收集的优先奖品,这取决于他/她的访问顺序。TSPPP的目标是找到n个客户访问的最大利润序列,并考虑到参观中所涉及的奖品和成本。
这个问题可以被看作是一个TSP变体,具有更一般的目标函数和相反的标准,针对解决方案,以某种方式考虑对客户的服务质量和交付优先级,最大化收集的奖品,同时最小化交付成本。TSPPP的一个简单例子是一辆面包车或面包车,它在机场接一群游客,并把每个游客送到他/她的酒店。一些游客愿意支付更多的费用,如果他们的费用,而其他游客则不会。司机希望选择最赚钱的旅行,然而,遵守这些优先奖品可能会增加总行程,从而增加旅行成本。另一个例子出现在机器调度问题的上下文中。具有顺序依赖的设置成本的单机调度是生产计划中的一个参考问题,它是一个众所周知的应用,其中机器所有者寻求最低设置成本生产计划。当工作优先级奖励也考虑在内时,问题就成为了TSPPP的应用。
我们不知道其他的研究已经直接处理了TSPPP,尽管可以在文献中发现相关的问题。一个例子是最小延迟问题(MLP)[14],也被称为旅行维修员问题,旅行送货员问题或具有累积成本[4,6,10,22,28]的旅行销售员问题。在MLP中,旅行销售员必须以所有客户的方式访问所有客户的总体等待时间(在这种情况下,如果弧(i,j)是旅行中遍历的第k个弧,成本由cijk =(n−)−ij给出)。MLP也可以被解释为一个具有序列依赖的处理时间的单机调度问题,其中人们寻求最小化作业[6]的总流时间。它也可以被视为一个特殊情况的旅行推销员问题(TDTSP)[15,22,25],遍历弧的成本两个节点i和j可能改变这个弧的位置(j)沿着哈密顿旅游[22](即dikj(k+1)= cijk)。事实上,TDTSP与本研究的TSPPP密切相关,如下一节所述。MLP的一个扩展是单车交付问题。不像TDTSP那样使用一般的时间依赖成本函数,这个扩展需要不同的需求量在每个节点i交付(注意,当每个客户的需求是一个单一单元时,MLP是一个单元,即di = 1)。
2. INTEGER QUADRATIC PROGRAM FOR TSPPP
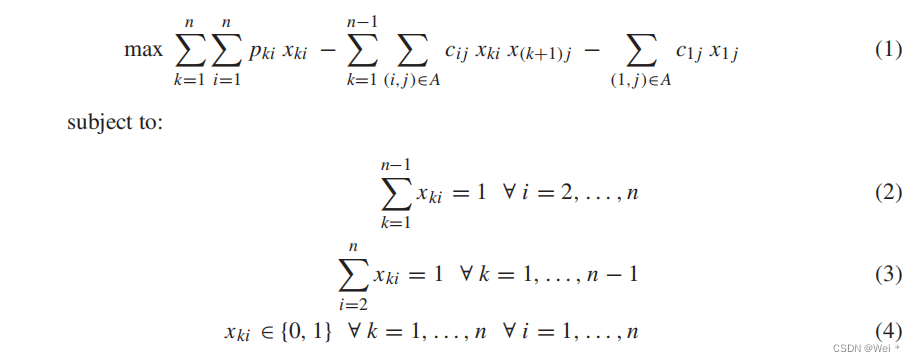
3. MIXED INTEGER LINEAR PROGRAMS FOR TSPPP
4. TABU SEARCH ALGORITHM FOR TSPPP
5. COMPUTATIONAL RESULTS
6. CONCLUDING REMARKS
一个旅行推销员基本上是为了销售商品。成本最小化只是一个最大利润目标的结果。这一观点已经在不同的研究中进行了探讨,以应对运输成本最小化的标准方法不一定意味着销售人员的最大利润目标的情况。本文研究了客户在旅行推销员路线中根据他们的访问顺序支付不同的优先奖励的特殊情况,称为旅行推销员优先奖励问题(TSPPP)。这种类型的销售人员福利是独立在使问题形式化的整数二次规划的线性包。据我们所知,在文献中还没有其他的研究直接处理了TSPPP。为了处理节点访问顺序,我们在库普曼斯和贝克曼[18]中探索了基于QAP的TSPPP表示。我们提出了来自这个QAP和其他模型的不同的MIP模型来处理TSPPP,以及一个有效的tabu搜索算法,能够解决更大的问题实例。
未来一个有趣的角度的研究是调查使用更有效的TDTSP配方处理TSPPP [1,16],以及探索TSPPP方法的应用程序在现实情况下,如在单机调度问题优先奖和旅游旅游[29]计划。另一个未来的研究将是将目前的tabu搜索算法与其他元启发式算法进行比较,如变量邻域搜索和进化算法。此外,对旅行推销路线中的所有节点进行访问的条件可能与某些应用无关,因此另一个有趣的研究方向是扩展目前的方法来处理TSPPP的奖金版本。
补充
相关文章:
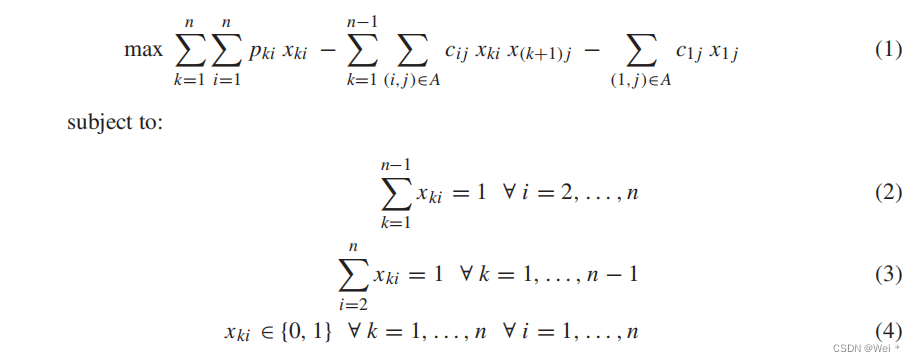
【论文阅读】MODELING AND SOLVING THE TRAVELING SALESMAN PROBLEM WITH PRIORITY PRIZES
文章目录 论文基本信息摘要1.引言2. INTEGER QUADRATIC PROGRAM FOR TSPPP3. MIXED INTEGER LINEAR PROGRAMS FOR TSPPP4. TABU SEARCH ALGORITHM FOR TSPPP5. COMPUTATIONAL RESULTS6. CONCLUDING REMARKS补充 论文基本信息 《MODELING AND SOLVING THE TRAVELING SALESMAN P…...

【CS.SE】使用 docker pull confluentinc/cp-kafka 的全面指南
文章目录 1 引言2 准备工作2.1 安装 Docker2.1.1 在 Linux 上安装 Docker2.1.2 在 macOS 上安装 Docker2.1.3 在 Windows 上安装 Docker 2.2 验证 Docker 安装 3 拉取 confluentinc/cp-kafka Docker 镜像3.1 拉取镜像3.2 验证镜像 4 运行 Kafka 容器4.1 启动 ZooKeeper4.2 启动…...

STM32快速入门(ADC数模转换)
STM32快速入门(ADC数模转换) 前言 ADC数模转换存在的意义就是将一些温度传感器、各自数据传感器产生的模拟信号转换成方便识别和计算的数字信号。 导航 图24 通用定时器框图: 图片截取自STM32 F1XX中文参考手册。还是以框图为中心&#x…...
Linux环境在非root用户中搭建(java-tomcat-redis)
注: 本文在内网(离线)环境,堡垒机中搭建,服务器不同可能有所差异,仅供参考 本文安装JDK-20.0.1版本,apache-tomcat-10.1.10版本,redis-6.2.15版本 本文服务器IP假设:192.168.88.133 root用户创建子用户并…...
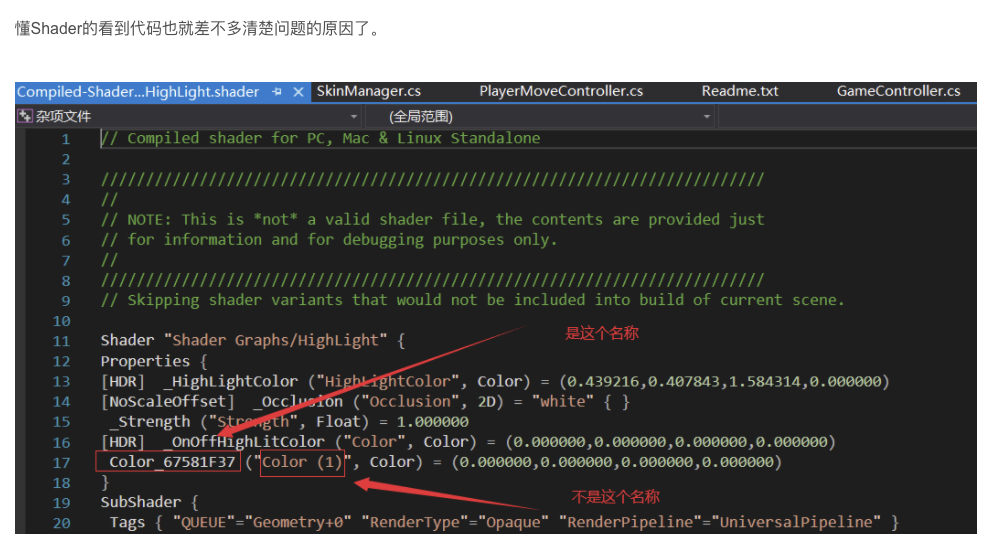
Unity 之 代码修改材质球贴图
Unity 之 代码修改材质球贴图 代码修改Shader:ShaderGraph:材质球包含属性 代码修改 meshRenderer.material.SetTexture("_Emission", texture);Shader: ShaderGraph: 材质球包含属性 materials[k].HasProperty("…...
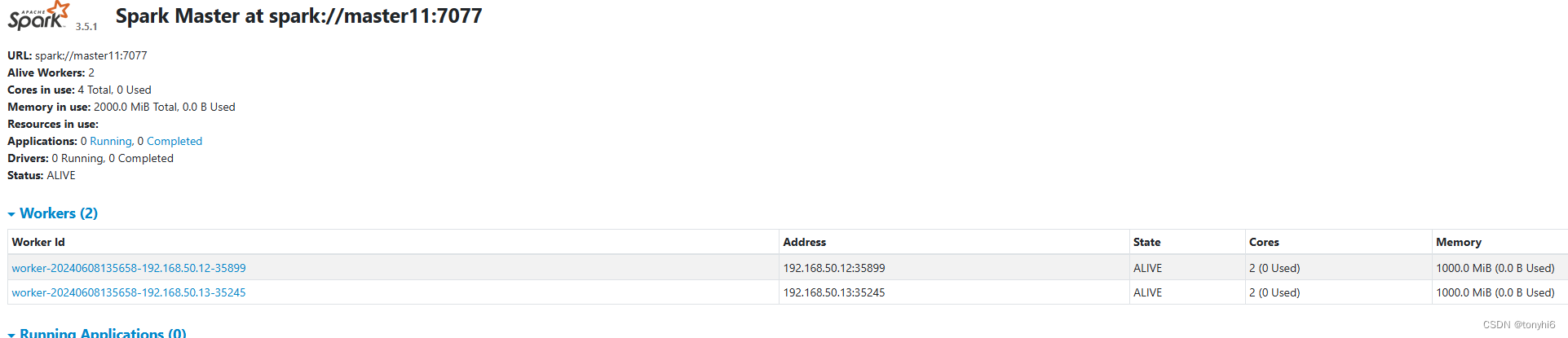
spark-3.5.1+Hadoop 3.4.0+Hive4.0 分布式集群 安装配置
Hadoop安装参考: Hadoop 3.4.0HBase2.5.8ZooKeeper3.8.4Hive4.0Sqoop 分布式高可用集群部署安装 大数据系列二-CSDN博客 一 下载:Downloads | Apache Spark 1 下载Maven – Welcome to Apache Maven # maven安装及配置教程 wget https://dlcdn.apache.org/maven/maven-3/3.8…...

Matlab实现GWO-CNN-LSTM-Mutilhead-Att灰狼算法卷积长短期记忆神经网络融合多头注意力机制预测 SCI顶级优化
数据预处理:准备和清理数据,包括数据的加载、特征提取、归一化等。 GWO (灰狼算法) 的实现:根据灰狼算法的原理和公式,编写 MATLAB 代码来初始化灰狼群体、计算适应度函数、更新位置等。 CNN (卷积神经网络) 的构建:使…...

RTKLIB之RTKPLOT画图工具
开源工具RTKLIB在业内如雷贯耳,其中的RTKPLOT最近正在学习,发现其功能之强大,前所未见,打开了新的思路。 使用思博伦GSS7000卫星导航模拟器,PosApp软件仿真一个载具位置 1,RTKPLOT支持DUT 串口直接输出的NMEA数据并…...

本地部署 RAGFlow
本地部署 RAGFlow 0. RAGFlow 是什么?1. 安装 wsl-ubuntu2. (可选)配置清华大学软件源3. 系统更新和安装构建工具4. 安装 Miniconda35. 安装 CUDA Toolkit6. 安装 git lfs7. 配置 Hugging Face 的缓存路径8. 配置 vm.max_map_count9. 安装 Docker Engine10. 安装 nginx11. 本地…...

php常用数据库操作
文章目录 PHP操作1. mysqli_connect() 连接数据库2. mysqli_close() 关闭数据库3. mysqli_num_rows 查询结果集中的行数4. mysqli_select_db 选择数据库的函数5. mysqli_query 常规的插入查找等6. header( )7.防止 sql 注入 PHP操作 1. mysqli_connect() 连接数据库 2. mysql…...
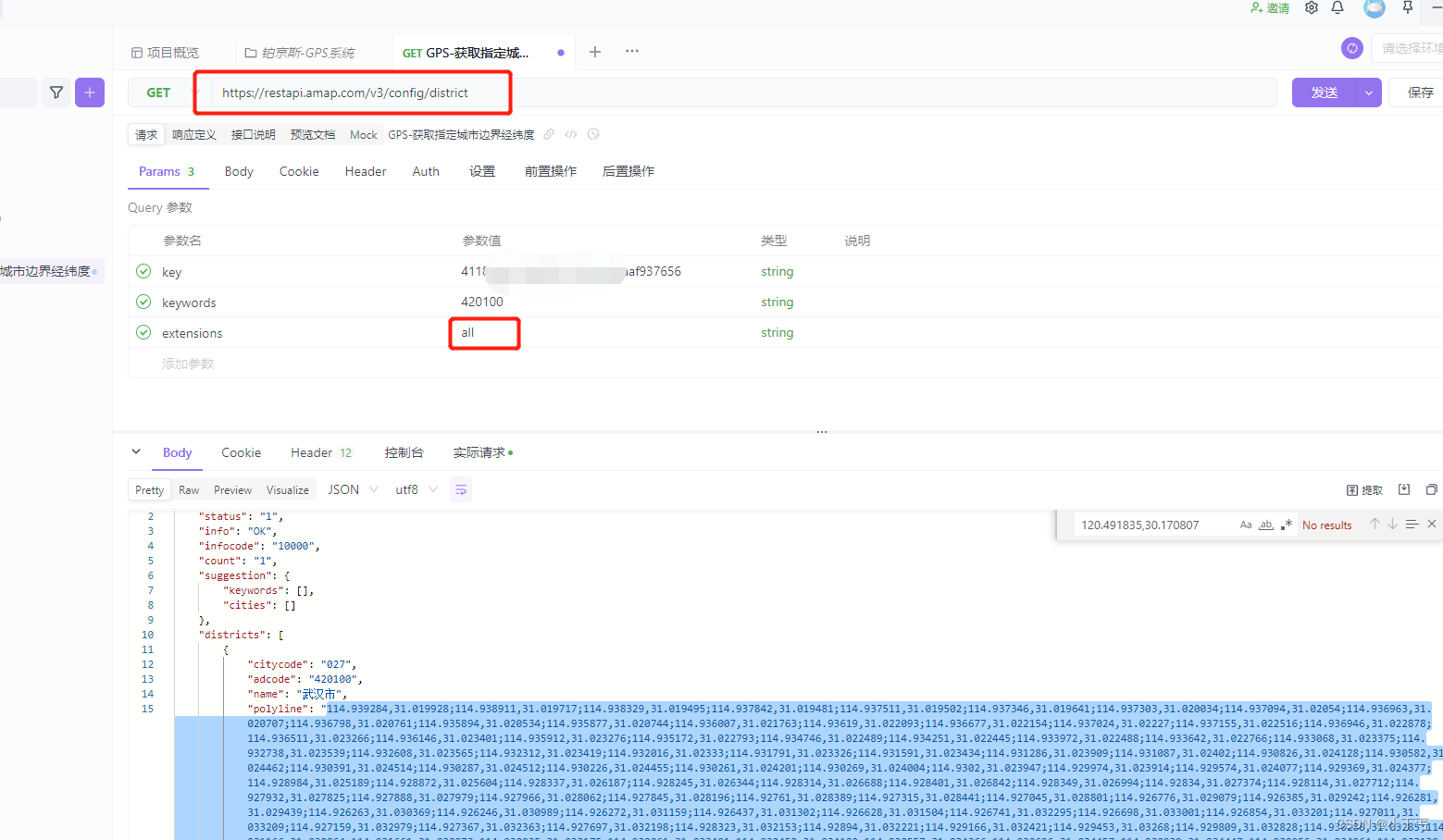
判断经纬度是否在某个城市内
一、从高德获取指定城市边界经纬度信息 通过apifox操作: 二、引入第三方jar包: maven地址:https://mvnrepository.com/ maven依赖: <dependency><groupId>org.locationtech.jts</groupId><artifactId>…...
Java——数组排序和查找
一、排序介绍 1、排序的概念 排序是将多个数据按照指定的顺序进行排列的过程。 2、排序的种类 排序可以分为两大类:内部排序和外部排序。 3、内部排序和外部排序 1)内部排序 内部排序是指数据在内存中进行排序,适用于数据量较小的情况…...

Flutter中防抖动和节流策略
什么是防抖和节流? 函数节流(throttle)与 函数防抖(debounce)都是为了限制函数的执行频次,以优化函数触发频率过高导致的响应速度跟不上触发频率,出现延迟,假死或卡顿的现象 是应对频…...

设计模式-中介者(调停者)模式(行为型)
中介者模式 中介者模式是一种行为型模式,又叫调停者模式,它是为了解决多个对象之间,多个类之间通信的复杂性,定义一个中介者对象来封装一些列对象之间的交互,使各个对象之间不同持有对方的引用就可以实现交互…...

HC-05蓝牙模块配置连接和使用
文章目录 1. 前期准备 2. 进入AT模式 3. 电脑串口配置 4. 配置过程 5. 主从机蓝牙连接 6. 蓝牙模块HC-05和电脑连接 1. 前期准备 首先需要准备一个USB转TTL连接器,电脑安装一个串口助手,然后按照下面的连接方式将其相连。 VCCVCCGNDGNDRXDTXDTXD…...

云上小知识:企业选择云服务的小Tips
企业在选择云服务模式时,应综合考虑以下几个关键因素: 1. 业务需求与场景 企业需要根据自身的业务特点和需求来选择合适的云服务模式。例如,如果企业的用户分布广泛,需要跨地域提供服务,那么公有云可能是更好的选择。…...

生成式人工智能 - Stable Diffusion 都使用了哪些技术?
一、Stable Diffusion简述 1、简述 Stable Diffusion在2022年8月开源,是由慕尼黑大学的CompVis研究团队开发的生成式人工神经网络。该项目由初创公司StabilityAI、CompVis和Runway合作开发,并得到了EleutherAI和LAION的支持。截至2022年10月,StabilityAI已筹集了1.01亿美元…...

React的useState的基础使用
import {useState} from react // 1.调用useState添加状态变量 // count 是新增的状态变量 // setCount 修改状态变量的方法 // 2.添加点击事件回调 // userState实现计数实例import {useState} from react// 使用组件 function App() {// 1.调用useState添加状态变量// coun…...
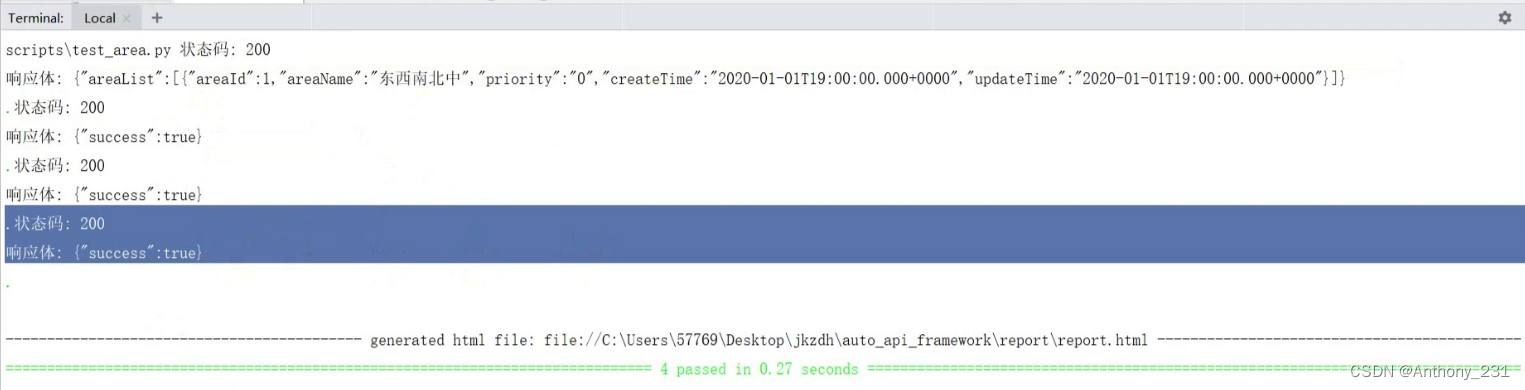
接口自动化Requests+Pytest基础实现
目录 1. 数据库以及数据库操作1.1 概念1.2 分类1.3 作用 2 python操作数据库的相关实现2.1 背景2.2 相关实现 3. pymysql基础3.1 整个流程3.2 案例3.3 Pymysql工具类封装 4 事务4.1 案例4.2 事务概念4.3 事务特征 5. requests库5.1 概念5.2 角色定位5.3 安装5.4 校验5.5 reques…...

深入解析Kafka消息传递的可靠性保证机制
深入解析Kafka消息传递的可靠性保证机制 Kafka在设计上提供了不同层次的消息传递保证,包括at most once(至多一次)、at least once(至少一次)和exactly once(精确一次)。每种保证通过不同的机制…...

业务系统对接大模型的基础方案:架构设计与关键步骤
业务系统对接大模型:架构设计与关键步骤 在当今数字化转型的浪潮中,大语言模型(LLM)已成为企业提升业务效率和创新能力的关键技术之一。将大模型集成到业务系统中,不仅可以优化用户体验,还能为业务决策提供…...

Python实现prophet 理论及参数优化
文章目录 Prophet理论及模型参数介绍Python代码完整实现prophet 添加外部数据进行模型优化 之前初步学习prophet的时候,写过一篇简单实现,后期随着对该模型的深入研究,本次记录涉及到prophet 的公式以及参数调优,从公式可以更直观…...

从零开始打造 OpenSTLinux 6.6 Yocto 系统(基于STM32CubeMX)(九)
设备树移植 和uboot设备树修改的内容同步到kernel将设备树stm32mp157d-stm32mp157daa1-mx.dts复制到内核源码目录下 源码修改及编译 修改arch/arm/boot/dts/st/Makefile,新增设备树编译 stm32mp157f-ev1-m4-examples.dtb \stm32mp157d-stm32mp157daa1-mx.dtb修改…...

MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

AI,如何重构理解、匹配与决策?
AI 时代,我们如何理解消费? 作者|王彬 封面|Unplash 人们通过信息理解世界。 曾几何时,PC 与移动互联网重塑了人们的购物路径:信息变得唾手可得,商品决策变得高度依赖内容。 但 AI 时代的来…...

Hive 存储格式深度解析:从 TextFile 到 ORC,如何选对数据存储方案?
在大数据处理领域,Hive 作为 Hadoop 生态中重要的数据仓库工具,其存储格式的选择直接影响数据存储成本、查询效率和计算资源消耗。面对 TextFile、SequenceFile、Parquet、RCFile、ORC 等多种存储格式,很多开发者常常陷入选择困境。本文将从底…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...
混合(Blending))
C++.OpenGL (20/64)混合(Blending)
混合(Blending) 透明效果核心原理 #mermaid-svg-SWG0UzVfJms7Sm3e {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-icon{fill:#552222;}#mermaid-svg-SWG0UzVfJms7Sm3e .error-text{fill…...

【Linux】Linux 系统默认的目录及作用说明
博主介绍:✌全网粉丝23W,CSDN博客专家、Java领域优质创作者,掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域✌ 技术范围:SpringBoot、SpringCloud、Vue、SSM、HTML、Nodejs、Python、MySQL、PostgreSQL、大数据、物…...
