【Python数据类型的奥秘】:构建程序基石,驾驭信息之海
文章目录
- 🚀Python数据类型
- 🌈1. 基本概念
- ⭐2. 转化
- 👊3. 数值运算
- 💥4. 数值运算扩展(math库常用函数)
🚀Python数据类型

🌈1. 基本概念
整数(int):整数是没有小数部分的数字。在Python中,整数可以是正数、负数或零。 整数类型在Python 3中没有大小限制,因此可以处理非常大的整数。可以使用内置函数“int()”将其他类型的对象转换为整数。
浮点数(float):浮点数是带有小数部分的数字。在Python中,浮点数可以是正数、负数或零。 Python使用IEEE 754标准来表示浮点数。然而,与整数不同,浮点数在进行运算时可能会遇到精度问题。可以使用内置函数"float()"将其他类型的对象转换为浮点数。
复数(complex):复数由实数部分和虚数部分组成。实数部分和虚数部分都可以是浮点数。在Python中,虚数部分用后缀“j”或“J”来表示。例如,(3+4j)表示实部为3,虚部为4的复数。可以使用内置函数“complex()”将其他类型的对象转换为复数。
布尔型(bool):布尔型只有两个值,True和False。它们通常用于控制流程语句中的条件。可以使用内置函数"bool()"将其他类型的对象转换为布尔类型。非零的数字、非空的字符串、非空的列表、元组或字典都会被转换为True,而其他的值都会被转换为False。
整数
- 整数:int
- 例如:1, 2, 3, 4, 5, 6…
浮点数
- 浮点数:float(其实就是小数 )
- 例如:1.10
布尔值
- 布尔值:bool
- 只有:True(逻辑真), False(逻辑假)
- True(逻辑真):在计算机里面数值形式为1
- False(逻辑假):在计算机里面数值型是0
- False(逻辑假)的情况:False,None,0 ,“”,(),[],{}
- 其余情况均为True(逻辑真)
复数
- 复数:complex
- 例如:1+2j: 1为实部,2j为虚部
- 复数了解即可,不做重点
⭐2. 转化
常规情况下数值类型是可以相互转化的,但是复数转化会比较特殊,接下来看看如下示例:
【示例1】:整形转布尔/浮点型
int1 = 1
# 将整数 通过 bool函数 转化为 bool类型
print(bool(int1))
# 将整数 通过 float函数 转化为 float类型
print(float(int1))
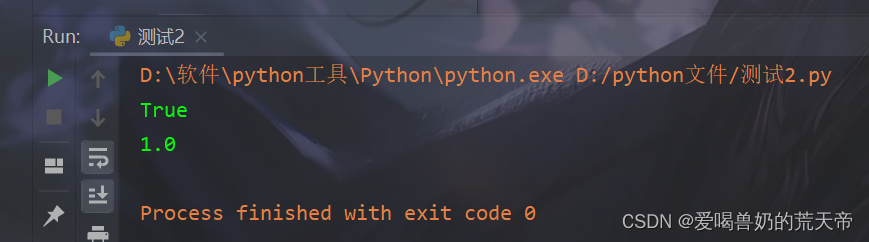
【示例2】:布尔型转整/浮点型
bool1 = True
# 将布尔值 通过 int函数 转化为 int类型
print(int(bool1))
# 将布尔值 通过 float函数 转化为 float类型
print(float(bool1))
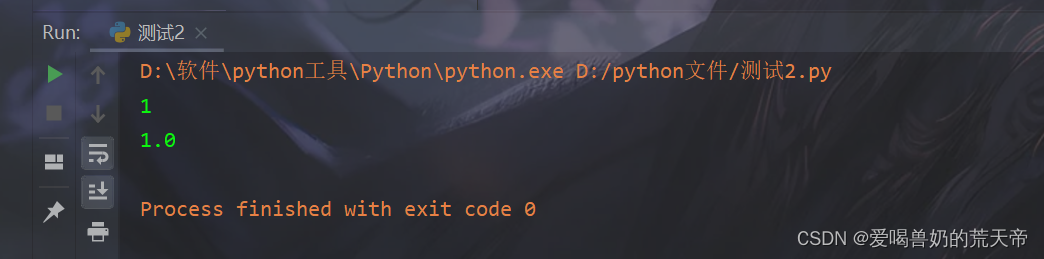
【示例3】:浮点型转布尔/整形
float1 = 1.23
# 将浮点数 通过 bool函数 转为 bool类型
print(bool(float1))
# 将浮点数 通过 int函数 转为 int类型
print(int(float1))

注意:False(逻辑假)的情况:False,None,0 ,“”,(),[],{} 除了这些情况均为True,不用纠结浮点数, 0.0 0.000 等均为0,因此布尔型为False;有想不通的地方实践出真理,理论得经得住实践的考验。
【示例4】:复数转整型
复数无法直接转换成整数(其它也一样)。因为复数包括实部和虚部两个部分,而整数只有一个部分。如果要将复数转换为整数,则需要确定如何处理实部和虚部。
a = 3 + 4j # 定义一个复数# 取实部、虚部并进行取整操作
real_part = int(a.real)
imag_part = int(a.imag)# 输出实部、虚部的整数值
print(real_part)
print(imag_part)
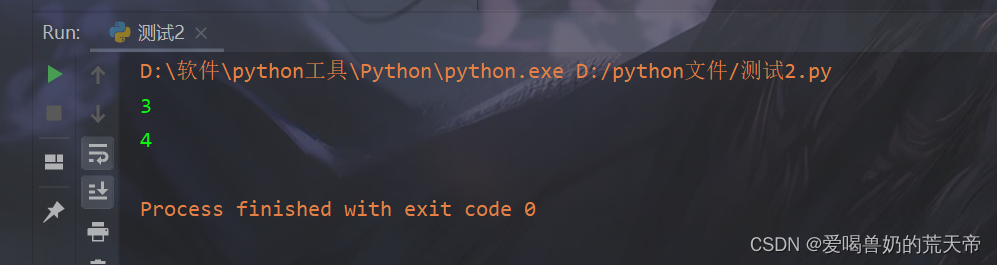
使用int()函数对复数的实部和虚部分别进行了取整操作,并分别存储在变量real_part和imag_part中。
注意:这种取整方式会丢失复数的一部分信息,因此可能会导致精度损失。所以,复数转换为整数需要考虑具体情况,并根据实际需求进行相应的数据处理。
👊3. 数值运算
| 符号 | 名 | 举例 | 结果 |
|---|---|---|---|
| + | 加 | 1+1 | 2 |
| - | 减 | 3-1 | 2 |
| * | 乘 | 3*2 | 6 |
| / | 除 | 6/2 | 3 |
| // | 向下取整 | 7//2 | 3(7/2 – 3.5) |
| % | 取余 | 7/2 | 1(7/2 – 3 – 1) |
| ** | 幂 | 2**4 | 16 (4个2相乘) |
- 加法运算符 (+): 用于将两个数值相加。
result = 10 + 5 # result = 15
- 减法运算符 (-): 用于从一个数值中减去另一个数值。
result = 10 - 5 # result = 5
- 乘法运算符 (*): 用于将两个数值相乘。
result = 10 * 5 # result = 50
- 除法运算符 (/): 用于将一个数值除以另一个数值,结果为浮点数。
result = 10 / 5 # result = 2.0
- 整除运算符 (//): 用于将一个数值除以另一个数值,结果向下取整为整数。
result = 10 // 5 # result = 2
- 取余运算符 (%): 用于计算除法的余数。
result = 10 % 3 # result = 1
- 幂运算符 (**): 用于计算一个数的幂。
result = 2 ** 3 # result = 8
- 取反运算符 (-): 用于改变数值的符号。
result = -10 # result = -10
- 增量赋值运算符: 如 +=, -=, *=, /=, //=, %= 和 **= ,用于将运算结果直接赋值回原变量。
x = 10
x += 5 # 相当于 x = x + 5; 现在 x = 15
💥4. 数值运算扩展(math库常用函数)
- math库(python内置模块)
- 调用:import math
Python 的 math 库是一个内置函数库,提供了各种数学运算的函数,包括三角函数、指数函数、对数函数、幂函数等等。使用 math 库中的函数可以方便地进行常见数值计算。
math 库中常用的函数:
- fabs(x):返回 x 的绝对值
- ceil(x):返回不小于 x 的最小整数
- floor(x):返回不大于 x 的最大整数
- sqrt(x):返回 x 的平方根
- pow(x, y):返回 x 的 y 次方
- exp(x):返回以 e 为底的 x 的指数
- log(x):返回以 e 为底的 x 的自然对数
- sin(x):返回 x 的正弦值,x 为弧度制
- cos(x):返回 x 的余弦值,x 为弧度制
- tan(x):返回 x 的正切值,x 为弧度制
- math.ceil(x) - 返回大于或等于 x 的最小整数。
import math
x = 3.7
print(math.ceil(x)) # 输出: 4
- math.floor(x) - 返回小于或等于 x 的最大整数。
x = 3.7
print(math.floor(x)) # 输出: 3
- math.sqrt(x) - 计算 x 的平方根。
x = 16
print(math.sqrt(x)) # 输出: 4.0
- math.exp(x) - 返回 e(自然对数的底)的 x 次幂。
x = 1
print(math.exp(x)) # 输出: 2.718281828459045
- math.log(x[, base]) - 计算 x 的对数,如果不提供 base,默认为自然对数。
x = 10
print(math.log(x)) # 输出自然对数
print(math.log(x, 10)) # 输出以10为底的对数
- math.sin(x) - 计算 x 弧度的正弦值。
x = math.pi / 2
print(math.sin(x)) # 输出: 1.0
- math.cos(x) - 计算 x 弧度的余弦值。
x = math.pi
print(math.cos(x)) # 输出接近: -1.0
- math.tan(x) - 计算 x 弧度的正切值。
x = math.pi / 4
print(math.tan(x)) # 输出接近: 0.9999999999999999
- math.pi - 提供圆周率 π 的值。
print(math.pi) # 输出: 3.141592653589793
- math.e - 提供自然对数的底 e 的值。
print(math.e) # 输出: 2.718281828459045
- math.pow(x, y) - 计算 x 的 y 次幂。
x = 2
y = 3
print(math.pow(x, y)) # 输出: 8.0
- math.fabs(x) - 返回 x 的绝对值,适用于浮点数。
x = -3.5
print(math.fabs(x)) # 输出: 3.5
- math.factorial(x) - 计算 x 的阶乘(x 必须是非负整数)。
x = 5
print(math.factorial(x)) # 输出: 120
- math.gcd(a, b) - 计算 a 和 b 的最大公约数。
a = 48
b = 18
print(math.gcd(a, b)) # 输出: 6
| 方法 | 作用 | 举例 |
|---|---|---|
| math.ceil | 向上取整 | math.ceil(1.24) # 2 |
| math.floor | 向下取整 | math.floor(1.24) # 1 |
| math.pi | 常数π,圆周率3.141592653589793 | |
| … |
注意:使用这些函数前需要先通过 import math 导入 math 模块。
相关文章:

【Python数据类型的奥秘】:构建程序基石,驾驭信息之海
文章目录 🚀Python数据类型🌈1. 基本概念⭐2. 转化👊3. 数值运算💥4. 数值运算扩展(math库常用函数) 🚀Python数据类型 🌈1. 基本概念 整数(int):整数是没有小数部分的数…...

vue使用html2canvas截图下载时,存在svg或者img或者特殊字体时截图不全的解决办法
使用html2canvas进行div截图时,存在svg和img的解决办法 写在前面:vue使用html2canvas截图时,存在svg或者img或者特殊字体时截图时空白,或者不全解决办法如下第一步,svg或者img先转base64(如果是特殊字体&am…...

机器学习----奥卡姆剃刀定律
奥卡姆剃刀定律(Occam’s Razor)是一条哲学原则,通常表述为“如无必要,勿增实体”(Entities should not be multiplied beyond necessity)或“在其他条件相同的情况下,最简单的解释往往是最好的…...

【设计模式】行为型设计模式之 模板方法模式
介绍 GOF 定义 模板方法模式 Template Method Design Pattern :模板方法模式在一个方法中定义一个算法骨架,并将某些步骤推迟到子类中去实现;模板方法在不改变算法整体结构的情况下,可以重新定义算法中的某些步骤。 代码举例 …...

智能合约中断言失败
断言失败: 断言(assert)在智能合约中用于确保内部逻辑的一致性和正确性,但如果使用不当,确实可能导致意外的合约终止或资金锁定。这是因为assert主要用于检测程序内部的错误,例如算法错误或逻辑错误&#…...

flink读取hive写入http接口
目录 0、创建hive数据 1、pom.xml 2、flink代码 3、sink 4、提交任务jar 5、flink-conf.yaml 6、数据接收 flink-1.17.2jdk1.8hive-3.1.3hadoop3.3.6passwordhttp0、创建hive数据 /cluster/hive/bin/beeline !connect jdbc:hive2://ip:10000 create database demo; d…...
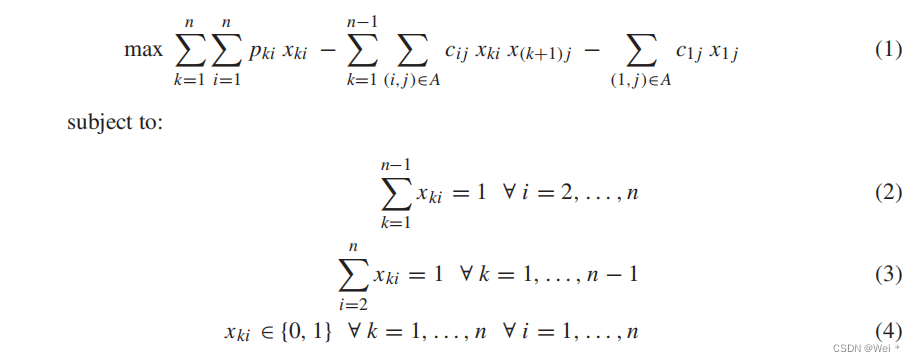
【论文阅读】MODELING AND SOLVING THE TRAVELING SALESMAN PROBLEM WITH PRIORITY PRIZES
文章目录 论文基本信息摘要1.引言2. INTEGER QUADRATIC PROGRAM FOR TSPPP3. MIXED INTEGER LINEAR PROGRAMS FOR TSPPP4. TABU SEARCH ALGORITHM FOR TSPPP5. COMPUTATIONAL RESULTS6. CONCLUDING REMARKS补充 论文基本信息 《MODELING AND SOLVING THE TRAVELING SALESMAN P…...

【CS.SE】使用 docker pull confluentinc/cp-kafka 的全面指南
文章目录 1 引言2 准备工作2.1 安装 Docker2.1.1 在 Linux 上安装 Docker2.1.2 在 macOS 上安装 Docker2.1.3 在 Windows 上安装 Docker 2.2 验证 Docker 安装 3 拉取 confluentinc/cp-kafka Docker 镜像3.1 拉取镜像3.2 验证镜像 4 运行 Kafka 容器4.1 启动 ZooKeeper4.2 启动…...

STM32快速入门(ADC数模转换)
STM32快速入门(ADC数模转换) 前言 ADC数模转换存在的意义就是将一些温度传感器、各自数据传感器产生的模拟信号转换成方便识别和计算的数字信号。 导航 图24 通用定时器框图: 图片截取自STM32 F1XX中文参考手册。还是以框图为中心&#x…...
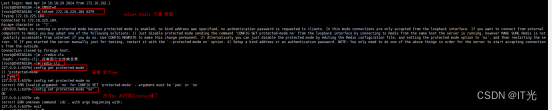
Linux环境在非root用户中搭建(java-tomcat-redis)
注: 本文在内网(离线)环境,堡垒机中搭建,服务器不同可能有所差异,仅供参考 本文安装JDK-20.0.1版本,apache-tomcat-10.1.10版本,redis-6.2.15版本 本文服务器IP假设:192.168.88.133 root用户创建子用户并…...
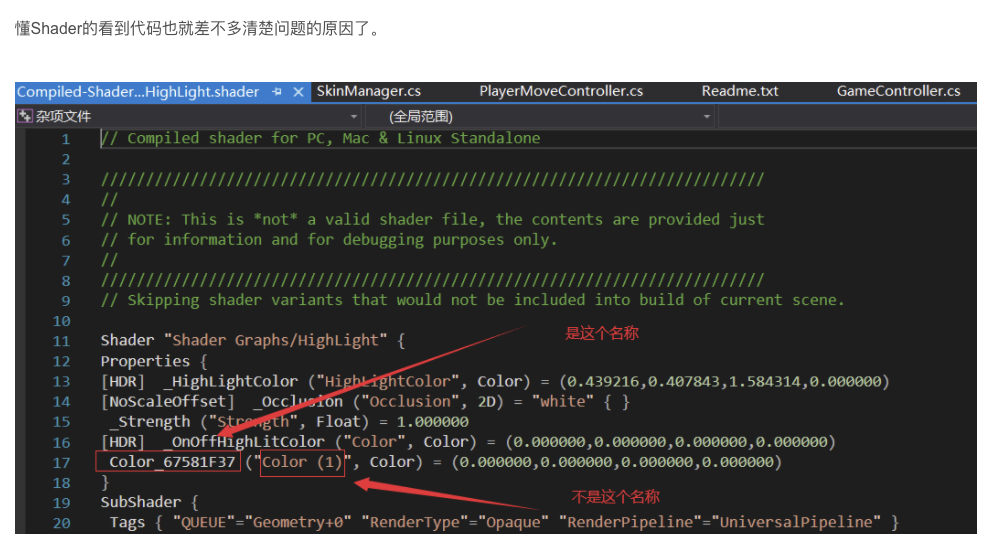
Unity 之 代码修改材质球贴图
Unity 之 代码修改材质球贴图 代码修改Shader:ShaderGraph:材质球包含属性 代码修改 meshRenderer.material.SetTexture("_Emission", texture);Shader: ShaderGraph: 材质球包含属性 materials[k].HasProperty("…...
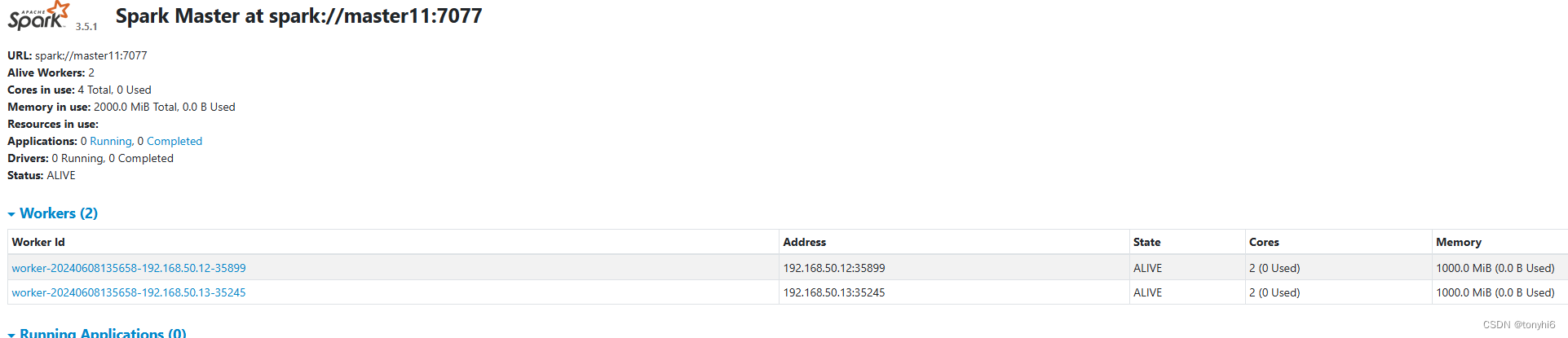
spark-3.5.1+Hadoop 3.4.0+Hive4.0 分布式集群 安装配置
Hadoop安装参考: Hadoop 3.4.0HBase2.5.8ZooKeeper3.8.4Hive4.0Sqoop 分布式高可用集群部署安装 大数据系列二-CSDN博客 一 下载:Downloads | Apache Spark 1 下载Maven – Welcome to Apache Maven # maven安装及配置教程 wget https://dlcdn.apache.org/maven/maven-3/3.8…...

Matlab实现GWO-CNN-LSTM-Mutilhead-Att灰狼算法卷积长短期记忆神经网络融合多头注意力机制预测 SCI顶级优化
数据预处理:准备和清理数据,包括数据的加载、特征提取、归一化等。 GWO (灰狼算法) 的实现:根据灰狼算法的原理和公式,编写 MATLAB 代码来初始化灰狼群体、计算适应度函数、更新位置等。 CNN (卷积神经网络) 的构建:使…...

RTKLIB之RTKPLOT画图工具
开源工具RTKLIB在业内如雷贯耳,其中的RTKPLOT最近正在学习,发现其功能之强大,前所未见,打开了新的思路。 使用思博伦GSS7000卫星导航模拟器,PosApp软件仿真一个载具位置 1,RTKPLOT支持DUT 串口直接输出的NMEA数据并…...

本地部署 RAGFlow
本地部署 RAGFlow 0. RAGFlow 是什么?1. 安装 wsl-ubuntu2. (可选)配置清华大学软件源3. 系统更新和安装构建工具4. 安装 Miniconda35. 安装 CUDA Toolkit6. 安装 git lfs7. 配置 Hugging Face 的缓存路径8. 配置 vm.max_map_count9. 安装 Docker Engine10. 安装 nginx11. 本地…...

php常用数据库操作
文章目录 PHP操作1. mysqli_connect() 连接数据库2. mysqli_close() 关闭数据库3. mysqli_num_rows 查询结果集中的行数4. mysqli_select_db 选择数据库的函数5. mysqli_query 常规的插入查找等6. header( )7.防止 sql 注入 PHP操作 1. mysqli_connect() 连接数据库 2. mysql…...
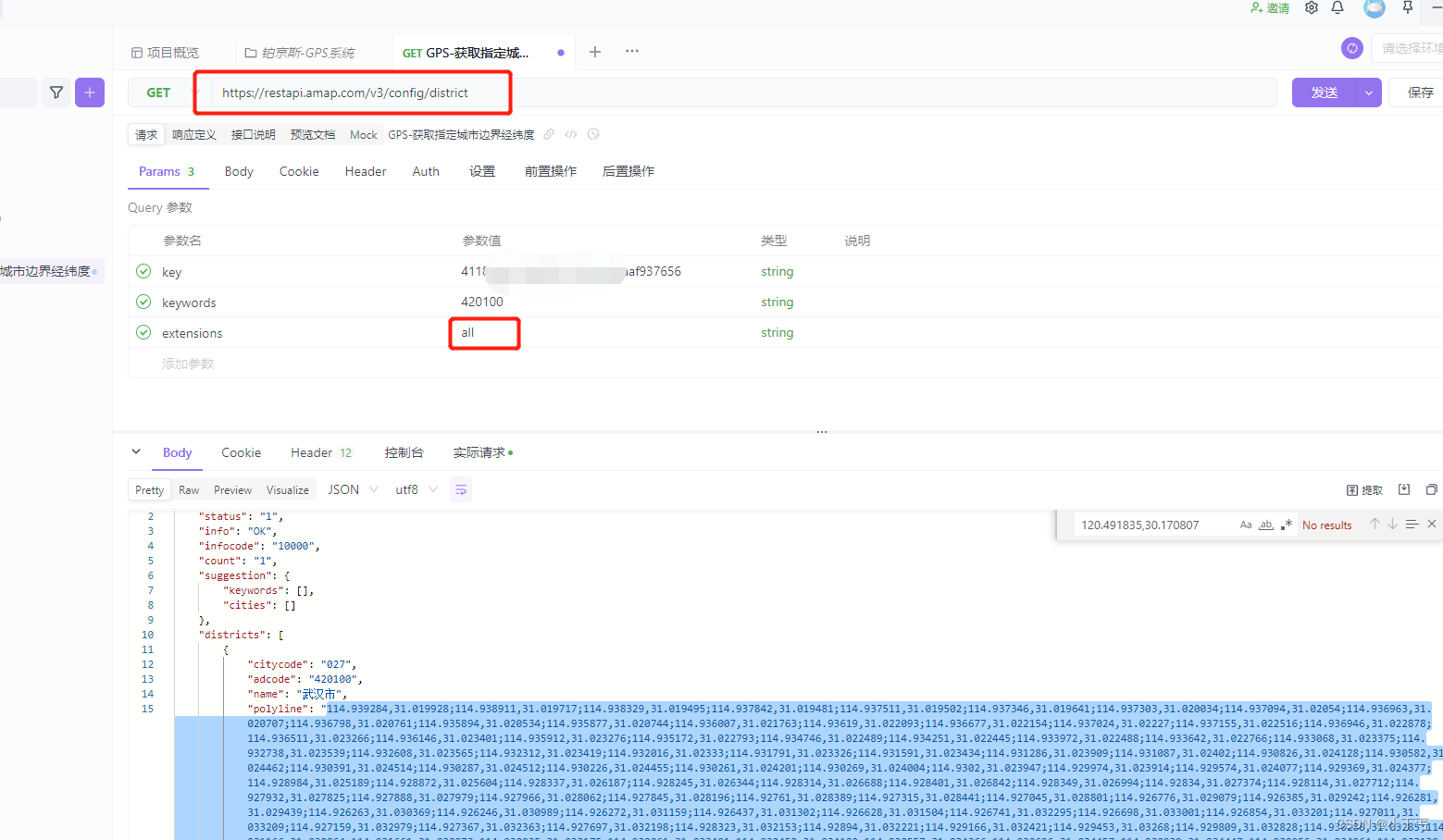
判断经纬度是否在某个城市内
一、从高德获取指定城市边界经纬度信息 通过apifox操作: 二、引入第三方jar包: maven地址:https://mvnrepository.com/ maven依赖: <dependency><groupId>org.locationtech.jts</groupId><artifactId>…...
Java——数组排序和查找
一、排序介绍 1、排序的概念 排序是将多个数据按照指定的顺序进行排列的过程。 2、排序的种类 排序可以分为两大类:内部排序和外部排序。 3、内部排序和外部排序 1)内部排序 内部排序是指数据在内存中进行排序,适用于数据量较小的情况…...

Flutter中防抖动和节流策略
什么是防抖和节流? 函数节流(throttle)与 函数防抖(debounce)都是为了限制函数的执行频次,以优化函数触发频率过高导致的响应速度跟不上触发频率,出现延迟,假死或卡顿的现象 是应对频…...

设计模式-中介者(调停者)模式(行为型)
中介者模式 中介者模式是一种行为型模式,又叫调停者模式,它是为了解决多个对象之间,多个类之间通信的复杂性,定义一个中介者对象来封装一些列对象之间的交互,使各个对象之间不同持有对方的引用就可以实现交互…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

web vue 项目 Docker化部署
Web 项目 Docker 化部署详细教程 目录 Web 项目 Docker 化部署概述Dockerfile 详解 构建阶段生产阶段 构建和运行 Docker 镜像 1. Web 项目 Docker 化部署概述 Docker 化部署的主要步骤分为以下几个阶段: 构建阶段(Build Stage):…...

Cursor实现用excel数据填充word模版的方法
cursor主页:https://www.cursor.com/ 任务目标:把excel格式的数据里的单元格,按照某一个固定模版填充到word中 文章目录 注意事项逐步生成程序1. 确定格式2. 调试程序 注意事项 直接给一个excel文件和最终呈现的word文件的示例,…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

stm32G473的flash模式是单bank还是双bank?
今天突然有人stm32G473的flash模式是单bank还是双bank?由于时间太久,我真忘记了。搜搜发现,还真有人和我一样。见下面的链接:https://shequ.stmicroelectronics.cn/forum.php?modviewthread&tid644563 根据STM32G4系列参考手…...

利用ngx_stream_return_module构建简易 TCP/UDP 响应网关
一、模块概述 ngx_stream_return_module 提供了一个极简的指令: return <value>;在收到客户端连接后,立即将 <value> 写回并关闭连接。<value> 支持内嵌文本和内置变量(如 $time_iso8601、$remote_addr 等)&a…...

R语言AI模型部署方案:精准离线运行详解
R语言AI模型部署方案:精准离线运行详解 一、项目概述 本文将构建一个完整的R语言AI部署解决方案,实现鸢尾花分类模型的训练、保存、离线部署和预测功能。核心特点: 100%离线运行能力自包含环境依赖生产级错误处理跨平台兼容性模型版本管理# 文件结构说明 Iris_AI_Deployme…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...
