【蓝桥杯】C语言常见高级算法
🌸个人主页:Yang-ai-cao
📕系列专栏:蓝桥杯 C语言
🍍博学而日参省乎己,知明而行无过矣
目录
🌸个人主页:Yang-ai-cao
📕系列专栏:蓝桥杯 C语言
🍍博学而日参省乎己,知明而行无过矣
一、动态规划(Dynamic Programming)
例子:斐波那契数列
动态规划解法
例子:0-1 背包问题
动态规划解法
二、贪心算法(Greedy Algorithm)
例子:活动选择问题
贪心算法解法
三、回溯算法(Backtracking)
例子:N皇后问题
回溯算法解法
四、分治算法(Divide and Conquer)
例子:归并排序(Merge Sort)
五、图算法(Graph Algorithms)
例子:Dijkstra 算法(单源最短路径)
贪心算法(Greedy Algorithm)
例子:霍夫曼编码(Huffman Coding)
总结
一、动态规划(Dynamic Programming)
例子:斐波那契数列
动态规划解法
#include <stdio.h>// 计算斐波那契数列的第 n 项
int fib(int n) {// 创建一个数组来存储斐波那契数列int f[n+1];f[0] = 0; // 第 0 项是 0f[1] = 1; // 第 1 项是 1// 通过迭代计算第 n 项for (int i = 2; i <= n; i++) {f[i] = f[i-1] + f[i-2]; // 当前项等于前两项之和}return f[n]; // 返回第 n 项
}int main() {int n = 10; // 计算第 10 项printf("Fibonacci number is %d\n", fib(n)); // 输出结果return 0;
}
例子:0-1 背包问题
动态规划解法
#include <stdio.h>// 返回两个整数中的最大值
int max(int a, int b) { return (a > b) ? a : b; }// 解决 0-1 背包问题
int knapSack(int W, int wt[], int val[], int n) {// 创建一个二维数组 K,用于存储子问题的解int K[n+1][W+1];// 填充 K 表for (int i = 0; i <= n; i++) {for (int w = 0; w <= W; w++) {if (i == 0 || w == 0) {K[i][w] = 0; // 基本情况:没有物品或容量为 0} else if (wt[i-1] <= w) {// 选择当前物品或不选择当前物品,取最大值K[i][w] = max(val[i-1] + K[i-1][w-wt[i-1]], K[i-1][w]);} else {K[i][w] = K[i-1][w]; // 当前物品不能放入背包}}}return K[n][W]; // 返回最大价值
}int main() {int val[] = {60, 100, 120}; // 物品的价值int wt[] = {10, 20, 30}; // 物品的重量int W = 50; // 背包的容量int n = sizeof(val)/sizeof(val[0]); // 物品的数量printf("Maximum value in Knapsack = %d\n", knapSack(W, wt, val, n)); // 输出结果return 0;
}
二、贪心算法(Greedy Algorithm)
例子:活动选择问题
贪心算法解法
#include <stdio.h>// 打印最大数量的可选活动
void printMaxActivities(int s[], int f[], int n) {int i = 0; // 第一个活动总是被选择printf("Selected activities: %d ", i);// 选择其余活动for (int j = 1; j < n; j++) {if (s[j] >= f[i]) { // 如果当前活动的开始时间大于等于上一个活动的结束时间printf("%d ", j);i = j; // 更新上一个被选择活动的索引}}printf("\n");
}int main() {int s[] = {1, 3, 0, 5, 8, 5}; // 活动的开始时间int f[] = {2, 4, 6, 7, 9, 9}; // 活动的结束时间int n = sizeof(s)/sizeof(s[0]); // 活动的数量printMaxActivities(s, f, n); // 输出结果return 0;
}
三、回溯算法(Backtracking)
例子:N皇后问题
回溯算法解法
#include <stdio.h>
#include <stdbool.h>#define N 4 // 棋盘大小// 打印棋盘
void printSolution(int board[N][N]) {for (int i = 0; i < N; i++) {for (int j = 0; j < N; j++) {printf(" %d ", board[i][j]);}printf("\n");}
}// 检查在 board[row][col] 放置皇后是否安全
bool isSafe(int board[N][N], int row, int col) {int i, j;// 检查当前行的左侧for (i = 0; i < col; i++)if (board[row][i])return false;// 检查左上对角线for (i = row, j = col; i >= 0 && j >= 0; i--, j--)if (board[i][j])return false;// 检查左下对角线for (i = row, j = col; j >= 0 && i < N; i++, j--)if (board[i][j])return false;return true;
}// 递归解决 N 皇后问题
bool solveNQUtil(int board[N][N], int col) {if (col >= N) // 所有皇后已放置return true;for (int i = 0; i < N; i++) {if (isSafe(board, i, col)) { // 检查放置在 board[i][col] 是否安全board[i][col] = 1; // 放置皇后if (solveNQUtil(board, col + 1)) // 递归放置其余皇后return true;board[i][col] = 0; // 回溯:移除皇后}}return false; // 如果无法放置皇后
}// 解决 N 皇后问题
bool solveNQ() {int board[N][N] = { {0, 0, 0, 0},{0, 0, 0, 0},{0, 0, 0, 0},{0, 0, 0, 0} };if (solveNQUtil(board, 0) == false) {printf("Solution does not exist");return false;}printSolution(board); // 打印解决方案return true;
}int main() {solveNQ(); // 解决问题return 0;
}
四、分治算法(Divide and Conquer)
例子:归并排序(Merge Sort)
#include <stdio.h>// 合并两个子数组
void merge(int arr[], int l, int m, int r) {int n1 = m - l + 1; // 左子数组的大小int n2 = r - m; // 右子数组的大小int L[n1], R[n2]; // 临时数组// 复制数据到临时数组 L[] 和 R[]for (int i = 0; i < n1; i++)L[i] = arr[l + i];for (int j = 0; j < n2; j++)R[j] = arr[m + 1 + j];// 合并临时数组到 arr[l..r]int i = 0, j = 0, k = l;while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;} else {arr[k] = R[j];j++;}k++;}// 复制 L[] 剩余元素while (i < n1) {arr[k] = L[i];i++;k++;}// 复制 R[] 剩余元素while (j < n2) {arr[k] = R[j];j++;k++;}
}// 归并排序
void mergeSort(int arr[], int l, int r) {if (l < r) {int m = l + (r - l) / 2; // 找到中点mergeSort(arr, l, m); // 排序左半部分mergeSort(arr, m + 1, r); // 排序右半部分merge(arr, l, m, r); // 合并已排序的部分}
}// 打印数组
void printArray(int A[], int size) {for (int i = 0; i < size; i++)printf("%d ", A[i]);printf("\n");
}int main() {int arr[] = {12, 11, 13, 5, 6, 7};int arr_size = sizeof(arr) / sizeof(arr[0]);printf("Given array is \n");printArray(arr, arr_size);mergeSort(arr, 0, arr_size - 1);printf("\nSorted array is \n");printArray(arr, arr_size);return 0;
}
五、图算法(Graph Algorithms)
例子:Dijkstra 算法(单源最短路径)
#include <stdio.h>
#include <limits.h>
#include <stdbool.h>#define V 9 // 顶点数量// 找到最小距离的顶点
int minDistance(int dist[], bool sptSet[]) {int min = INT_MAX, min_index;for (int v = 0; v < V; v++)if (sptSet[v] == false && dist[v] <= min)min = dist[v], min_index = v;return min_index;
}// 打印解
void printSolution(int dist[], int n) {printf("Vertex \t Distance from Source\n");for (int i = 0; i < V; i++)printf("%d \t\t %d\n", i, dist[i]);
}// Dijkstra 算法
void dijkstra(int graph[V][V], int src) {int dist[V]; // 最短距离数组bool sptSet[V]; // sptSet[i] 为 true 表示顶点 i 已包含在最短路径树中// 初始化所有距离为无穷大,sptSet[] 为 falsefor (int i = 0; i < V; i++)dist[i] = INT_MAX, sptSet[i] = false;dist[src] = 0; // 源顶点距离为 0for (int count = 0; count < V - 1; count++) {int u = minDistance(dist, sptSet); // 选取最小距离顶点sptSet[u] = true; // 标记为已处理for (int v = 0; v < V; v++)if (!sptSet[v] && graph[u][v] && dist[u] != INT_MAX && dist[u] + graph[u][v] < dist[v])dist[v] = dist[u] + graph[u][v]; // 更新距离}printSolution(dist, V); // 打印结果
}int main() {int graph[V][V] = { {0, 4, 0, 0, 0, 0, 0, 8, 0},{4, 0, 8, 0, 0, 0, 0, 11, 0},{0, 8, 0, 7, 0, 4, 0, 0, 2},{0, 0, 7, 0, 9, 14, 0, 0, 0},{0, 0, 0, 9, 0, 10, 0, 0, 0},{0, 0, 4, 14, 10, 0, 2, 0, 0},{0, 0, 0, 0, 0, 2, 0, 1, 6},{8, 11, 0, 0, 0, 0, 1, 0, 7},{0, 0, 2, 0, 0, 0, 6, 7, 0} };dijkstra(graph, 0); // 调用 Dijkstra 算法return 0;
}
贪心算法(Greedy Algorithm)
例子:霍夫曼编码(Huffman Coding)
#include <stdio.h>
#include <stdlib.h>#define MAX_TREE_HT 100// 最小堆节点
struct MinHeapNode {char data; // 字符unsigned freq; // 频率struct MinHeapNode *left, *right; // 左右子节点
};// 最小堆
struct MinHeap {unsigned size; // 当前大小unsigned capacity; // 容量struct MinHeapNode **array; // 数组指针
};// 创建新节点
struct MinHeapNode* newNode(char data, unsigned freq) {struct MinHeapNode* temp = (struct MinHeapNode*)malloc(sizeof(struct MinHeapNode));temp->left = temp->right = NULL;temp->data = data;temp->freq = freq;return temp;
}// 创建最小堆
struct MinHeap* createMinHeap(unsigned capacity) {struct MinHeap* minHeap = (struct MinHeap*)malloc(sizeof(struct MinHeap));minHeap->size = 0;minHeap->capacity = capacity;minHeap->array = (struct MinHeapNode**)malloc(minHeap->capacity * sizeof(struct MinHeapNode*));return minHeap;
}// 交换两个最小堆节点
void swapMinHeapNode(struct MinHeapNode** a, struct MinHeapNode** b) {struct MinHeapNode* t = *a;*a = *b;*b = t;
}// 最小堆化
void minHeapify(struct MinHeap* minHeap, int idx) {int smallest = idx;int left = 2 * idx + 1;int right = 2 * idx + 2;if (left < minHeap->size && minHeap->array[left]->freq < minHeap->array[smallest]->freq)smallest = left;if (right < minHeap->size && minHeap->array[right]->freq < minHeap->array[smallest]->freq)smallest = right;if (smallest != idx) {swapMinHeapNode(&minHeap->array[smallest], &minHeap->array[idx]);minHeapify(minHeap, smallest);}
}// 检查是否只有一个元素
int isSizeOne(struct MinHeap* minHeap) {return (minHeap->size == 1);
}// 提取最小值节点
struct MinHeapNode* extractMin(struct MinHeap* minHeap) {struct MinHeapNode* temp = minHeap->array[0];minHeap->array[0] = minHeap->array[minHeap->size - 1];--minHeap->size;minHeapify(minHeap, 0);return temp;
}// 插入节点到最小堆
void insertMinHeap(struct MinHeap* minHeap, struct MinHeapNode* minHeapNode) {++minHeap->size;int i = minHeap->size - 1;while (i && minHeapNode->freq < minHeap->array[(i - 1) / 2]->freq) {minHeap->array[i] = minHeap->array[(i - 1) / 2];i = (i - 1) / 2;}minHeap->array[i] = minHeapNode;
}// 构建最小堆
void buildMinHeap(struct MinHeap* minHeap) {int n = minHeap->size - 1;for (int i = (n - 1) / 2; i >= 0; --i)minHeapify(minHeap, i);
}// 打印数组
void printArr(int arr[], int n) {for (int i = 0; i < n; ++i)printf("%d", arr[i]);printf("\n");
}// 检查是否是叶子节点
int isLeaf(struct MinHeapNode* root) {return !(root->left) && !(root->right);
}// 创建并构建最小堆
struct MinHeap* createAndBuildMinHeap(char data[], int freq[], int size) {struct MinHeap* minHeap = createMinHeap(size);for (int i = 0; i < size; ++i)minHeap->array[i] = newNode(data[i], freq[i]);minHeap->size = size;buildMinHeap(minHeap);return minHeap;
}// 构建霍夫曼树
struct MinHeapNode* buildHuffmanTree(char data[], int freq[], int size) {struct MinHeapNode *left, *right, *top;struct MinHeap* minHeap = createAndBuildMinHeap(data, freq, size);while (!isSizeOne(minHeap)) {left = extractMin(minHeap);right = extractMin(minHeap);top = newNode('$', left->freq + right->freq);top->left = left;top->right = right;insertMinHeap(minHeap, top);}return extractMin(minHeap);
}// 打印霍夫曼编码
void printCodes(struct MinHeapNode* root, int arr[], int top) {if (root->left) {arr[top] = 0;printCodes(root->left, arr, top + 1);}if (root->right) {arr[top] = 1;printCodes(root->right, arr, top + 1);}if (isLeaf(root)) {printf("%c: ", root->data);printArr(arr, top);}
}// 霍夫曼编码
void HuffmanCodes(char data[], int freq[], int size) {struct MinHeapNode* root = buildHuffmanTree(data, freq, size);int arr[MAX_TREE_HT], top = 0;printCodes(root, arr, top);
}int main() {char arr[] = {'a', 'b', 'c', 'd', 'e', 'f'};int freq[] = {5, 9, 12, 13, 16, 45};int size = sizeof(arr) / sizeof(arr[0]);HuffmanCodes(arr, freq, size); // 调用霍夫曼编码return 0;
}
总结
- 分治算法通过递归地将问题分解为子问题,解决这些子问题然后合并其解,适用于排序、搜索等问题。
- 图算法如Dijkstra算法,通过逐步扩展最短路径树,找到图中从单个源到所有其他顶点的最短路径。
- 贪心算法如霍夫曼编码,通过每一步选择局部最优解,最终构建出全局最优解,适用于数据压缩等问题。
- 贪心算法每一步都选择当前最优的选择,适用于能够通过局部最优达到全局最优的问题。
- 回溯算法系统地搜索所有可能的解,通过尝试构建解并在不满足条件时回溯,适用于需要探索所有可能解的问题。
- 动态规划通过存储子问题的解来避免重复计算,适用于有重叠子问题和最优子结构的问题。
相关文章:

【蓝桥杯】C语言常见高级算法
🌸个人主页:Yang-ai-cao 📕系列专栏:蓝桥杯 C语言 🍍博学而日参省乎己,知明而行无过矣 目录 🌸个人主页:Yang-ai-cao 📕系列专栏:蓝桥杯 C语言 &a…...
FastJson
目录 FastJson 新建一个SpringBoot项目 pom.xml 一、JavaBean与JSON数据相互转换 LoginController FastJsonApplication启动类 编辑二、FastJson的JSONField注解 Log实体类 TestLog测试类 三、FastJson对JSON数据的增、删、改、查 TestCrud FastJson 1、JSON使用手册…...

Web3设计风格和APP设计风格
Web3设计风格和传统APP设计风格在视觉和交互设计上有一些显著的区别。这些差异主要源于Web3技术和理念的独特性,以及它们在用户体验和界面设计中的具体应用。以下是Web3设计风格与传统APP设计风格的主要区别。北京木奇移动技术有限公司,专业的软件外包开…...
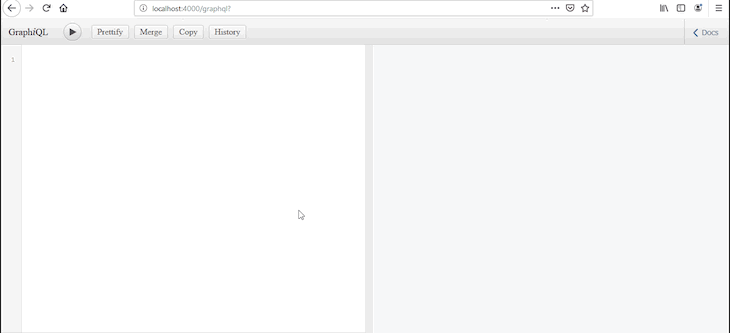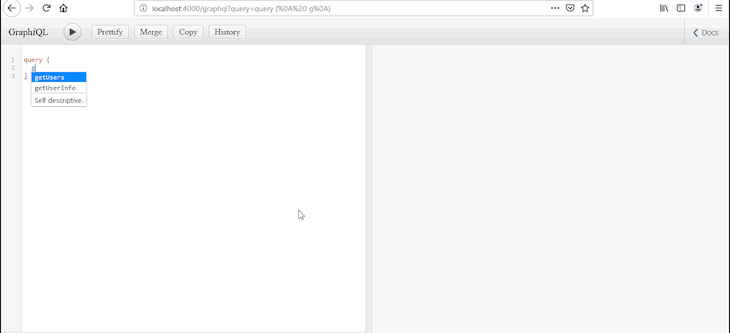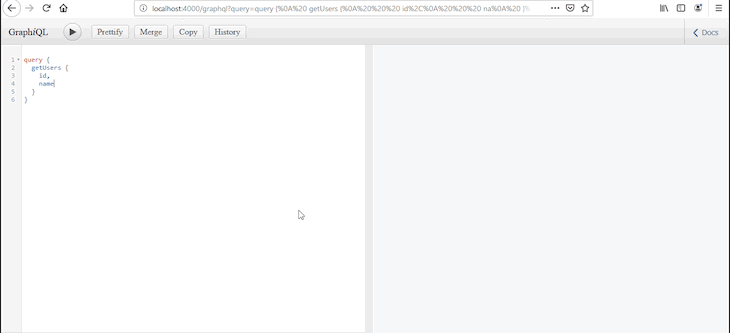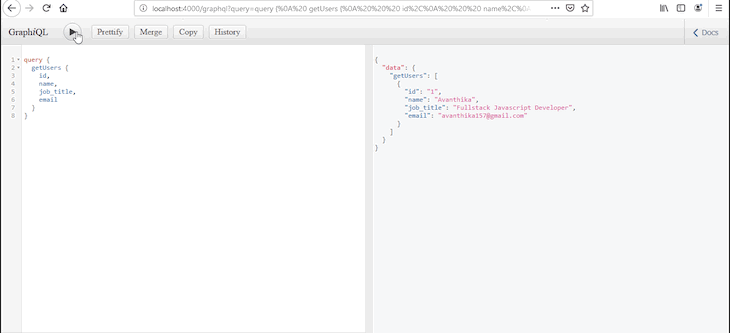
使用React和GraphQL进行CRUD:完整教程与示例
在本教程中,我们将向您展示如何使用GraphQL和React实现简单的端到端CRUD操作。我们将介绍使用React Hooks读取和修改数据的简单示例。我们还将演示如何使用Apollo Client实现身份验证、错误处理、缓存和乐观UI。 什么是React? React是一个用于构建用户…...

matplotlib 动态显示训练过程中的数据和模型的决策边界
文章目录 Github官网文档简介动态显示训练过程中的数据和模型的决策边界安装源码 Github https://github.com/matplotlib/matplotlib 官网 https://matplotlib.org/stable/ 文档 https://matplotlib.org/stable/api/index.html 简介 matplotlib 是 Python 中最常用的绘图…...

【学术小白成长之路】02三方演化博弈(基于复制动态方程)期望与复制动态方程
从本专栏开始,笔者正式研究演化博弈分析,其中涉及到双方演化博弈分析,三方演化博弈分析,复杂网络博弈分析等等。 先阅读了大量相关的博弈分析的文献,总结了现有的研究常用的研究流程,针对每个流程进行拆解。…...

短剧看剧系统投流版系统搭建,前端uni-app
目录 前言: 一、短剧看剧系统常规款短剧系统和投流版的区别? 二、后端体系 1.管理端: 2.代理投流端 三、功能区别 总结: 前言: 23年上半年共上新微短剧481部,相较于2022年全年上新的454部࿰…...

最新的ffmepg.js前端VUE3实现视频、音频裁剪上传功能
package.json "dependencies": {"ffmpeg/ffmpeg": "^0.12.10","ffmpeg/util": "^0.12.1" }vue3组件代码 根据需要更改 <script setup lang"ts"> import { FFmpeg } from ffmpeg/ffmpeg; import { fetchF…...

“Apache Kylin 实战指南:从安装到高级优化的全面教程
Apache Kylin是一个开源的分布式分析引擎,它提供了在Hadoop/Spark之上的SQL查询接口及多维分析(OLAP)能力,支持超大规模数据的亚秒级查询。以下是Kylin的入门教程,帮助您快速上手并使用这个强大的工具。 1. 安装Kylin Apache Kylin的安装是一个关键步骤,它要求您具备一…...

【iOS】内存泄漏检查及原因分析
目录 为什么要检测内存泄漏?什么是内存泄漏?内存泄漏排查方法1. 使用Zombie Objects2. 静态分析3. 动态分析方法定位修改Leaks界面分析Call Tree的四个选项: 内存泄漏原因分析1. Leaked Memory:应用程序未引用的、不能再次使用或释…...

“深入探讨Java中的对象拷贝:浅拷贝与深拷贝的差异与应用“
前言:在Java编程中,深拷贝(Deep Copy)与浅拷贝(Shallow Copy)是两个非常重要的概念。它们涉及到对象在内存中的复制方式,对于理解对象的引用、内存管理以及数据安全都至关重要。 ✨✨✨这里是秋…...

Docker 进入指定容器内部(以Mysql为例)
文章目录 一、启动容器二、查看容器是否启动三、进入容器内部 一、启动容器 这个就不多说了 直接docker run… 二、查看容器是否启动 查看正在运行的容器 docker ps查看所有的容器 docker ps -a结果如下图所示: 三、进入容器内部 通过CONTAINER ID进入到容器…...

计算机网络-数制转换与子网划分
目录 一、了解数制 1、计算机的数制 2、二进制 3、八进制 4、十进制 5、十六进制 二、数制转换 1、二进制转十进制 2、八进制转十进制 3、十六进制转十进制 4、十进制转二进制 5、十进制转八进制 6、十进制转十六进制 三、子网划分 1、IP地址定义 2、IP的两种协…...
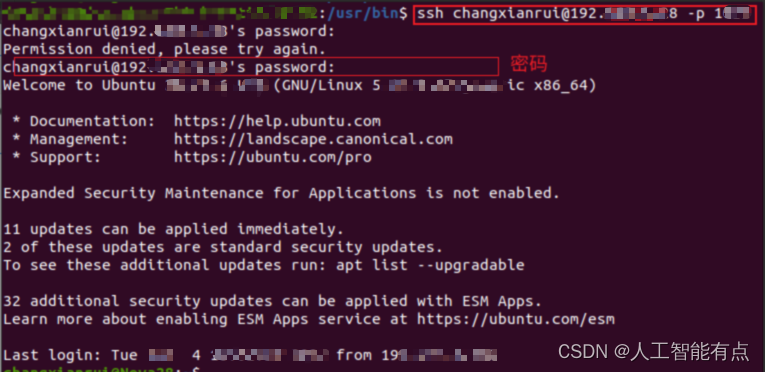
【ssh命令】ssh登录远程服务器
命令格式:ssh 用户名主机IP # 使用非默认端口: -p 端口号 ssh changxianrui192.168.100.100 -p 1022 # 使用默认端口 22 ssh changxianrui192.168.100.100 然后输入密码,就可以登录进去了。...
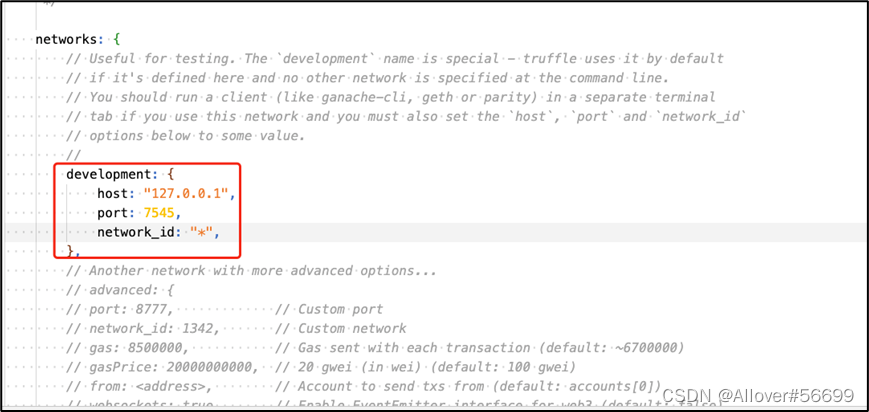
【区块链】truffle测试
配置区块链网络 启动Ganache软件 使用VScode打开项目的wordspace 配置对外访问的RPC接口为7545,配置项目的truffle-config.js实现与新建Workspace的连接。 创建项目 创建一个新的目录 mkdir MetaCoin cd MetaCoin下载metacoin盒子 truffle unbox metacoincontra…...

【AIGC调研系列】chatTTS与GPT-SoVITS的对比优劣势
ChatTTS和GPT-SoVITS都是在文本转语音(TTS)领域的重要开源项目,但它们各自有不同的优势和劣势。 ChatTTS 优点: 多语言支持:ChatTTS支持中英文,并且能够生成高质量、自然流畅的对话语音[4][10][13]。细粒…...

LLVM Cpu0 新后端10
想好好熟悉一下llvm开发一个新后端都要干什么,于是参考了老师的系列文章: LLVM 后端实践笔记 代码在这里(还没来得及准备,先用网盘暂存一下): 链接: https://pan.baidu.com/s/1yLAtXs9XwtyEzYSlDCSlqw?…...
)
k8s面试题大全,保姆级的攻略哦(二)
目录 三十六、pod的定义中有个command和args参数,这两个参数不会和docker镜像的entrypointc冲突吗? 三十七、标签及标签选择器是什么,如何使用? 三十八、service是如何与pod关联的? 三十九、service的域名解析格式…...
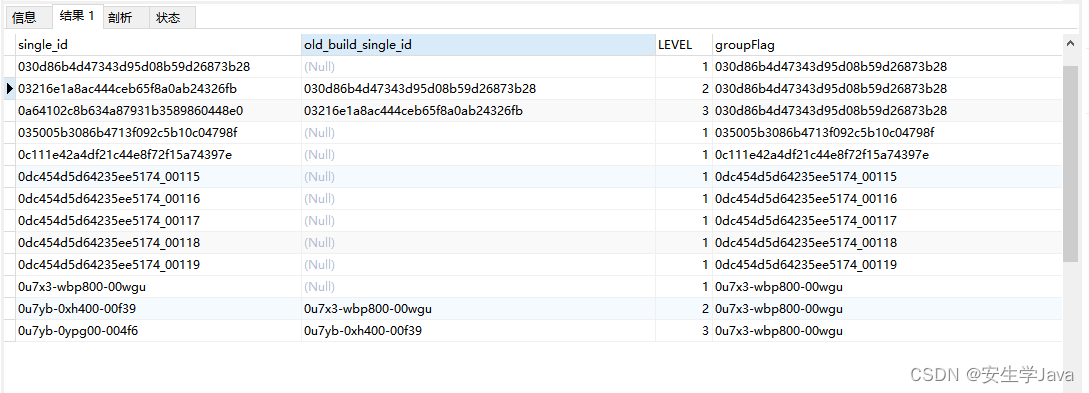
Mysql:通过一张表里的父子级,递归查询并且分组分级
递归函数WITH RECURSIVE语法 WITH RECURSIVE cte_name (column_list) AS (SELECT initial_query_resultUNION [ALL]SELECT recursive_queryFROM cte_nameWHERE condition ) SELECT * FROM cte_name; WITH RECURSIVE 关键字:表示要使用递归查询的方式处理数据。 c…...
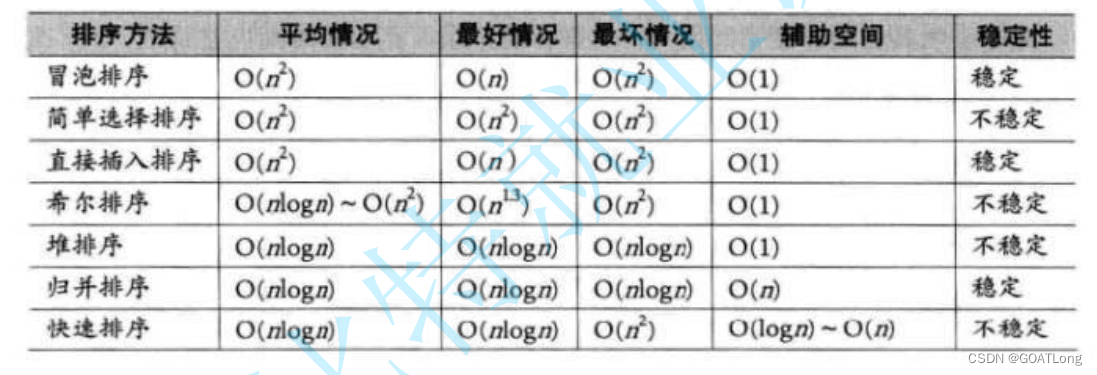
数据结构之排序算法
目录 1. 插入排序 1.1.1 直接插入排序代码实现 1.1.2 直接插入排序的特性总结 1.2.1 希尔排序的实现 1.2.2 希尔排序的特性总结 2. 选择排序 2.1.1 选择排序 2.1.2 选择排序特性 2.2.1 堆排序 2.2.2 堆排序特性 3. 交换排序 3.1.1 冒泡排序 3.1.2 冒泡排序的特性 …...

IDEA运行Tomcat出现乱码问题解决汇总
最近正值期末周,有很多同学在写期末Java web作业时,运行tomcat出现乱码问题,经过多次解决与研究,我做了如下整理: 原因: IDEA本身编码与tomcat的编码与Windows编码不同导致,Windows 系统控制台…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Ascend NPU上适配Step-Audio模型
1 概述 1.1 简述 Step-Audio 是业界首个集语音理解与生成控制一体化的产品级开源实时语音对话系统,支持多语言对话(如 中文,英文,日语),语音情感(如 开心,悲伤)&#x…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...

Unity中的transform.up
2025年6月8日,周日下午 在Unity中,transform.up是Transform组件的一个属性,表示游戏对象在世界空间中的“上”方向(Y轴正方向),且会随对象旋转动态变化。以下是关键点解析: 基本定义 transfor…...

加密通信 + 行为分析:运营商行业安全防御体系重构
在数字经济蓬勃发展的时代,运营商作为信息通信网络的核心枢纽,承载着海量用户数据与关键业务传输,其安全防御体系的可靠性直接关乎国家安全、社会稳定与企业发展。随着网络攻击手段的不断升级,传统安全防护体系逐渐暴露出局限性&a…...

在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南
在RK3588上搭建ROS1环境:创建节点与数据可视化实战指南 背景介绍完整操作步骤1. 创建Docker容器环境2. 验证GUI显示功能3. 安装ROS Noetic4. 配置环境变量5. 创建ROS节点(小球运动模拟)6. 配置RVIZ默认视图7. 创建启动脚本8. 运行可视化系统效果展示与交互技术解析ROS节点通…...

对象回调初步研究
_OBJECT_TYPE结构分析 在介绍什么是对象回调前,首先要熟悉下结构 以我们上篇线程回调介绍过的导出的PsProcessType 结构为例,用_OBJECT_TYPE这个结构来解析它,0x80处就是今天要介绍的回调链表,但是先不着急,先把目光…...
